结构力学第9章__力矩分配法(新)
- 格式:ppt
- 大小:630.50 KB
- 文档页数:26


结构力学下多结点力矩分配法引言在结构力学中,力矩分配法是一种常见的分析方法,用于计算多结点约束下的力矩分配。
多结点力矩分配法通过将外加载荷分配给结构中的各个节点,以确定每个节点承载的力矩。
本文将介绍结构力学下的多结点力矩分配法的基本原理和计算方法。
原理多结点力矩分配法的原理基于以下假设:1.结构是一个刚体,可以忽略其变形。
2.结构中的每个节点都可以承受力矩,且力矩的分配是均匀的。
基于这些假设,我们可以将外加载荷分配给结构中的各个节点,并计算每个节点承载的力矩。
力矩的分配是根据节点间的刚性关系来确定的。
计算方法多结点力矩分配法可以通过以下步骤进行计算:1.确定结构的节点个数和节点编号。
2.根据结构的几何形状和边界条件,建立节点间的刚性关系。
3.将外加载荷均匀地分配给每个节点。
可以根据结构的几何形状和边界条件,考虑节点之间的距离和角度来确定各个节点的分配比例。
4.根据节点间的刚性关系,计算每个节点承载的力矩。
可以使用刚体平衡条件来计算力矩的分配。
5.检查计算结果的合理性。
根据结构的几何形状和边界条件,验证计算得到的力矩分配是否符合工程实际。
示例下面以一个简单的桁架结构为例,介绍多结点力矩分配法的计算方法。
假设桁架结构的节点个数为4,节点编号分别为1, 2, 3和4。
外加载荷为M,沿结构的纵向均匀分布。
根据桁架结构的几何形状和边界条件,建立节点间的刚性关系。
假设节点1和节点2之间的刚性系数为k1,节点2和节点3之间的刚性系数为k2,节点3和节点4之间的刚性系数为k3。
将外加载荷均匀地分配给每个节点。
假设节点1承载的力矩为M1,节点2承载的力矩为M2,节点3承载的力矩为M3,节点4承载的力矩为M4,可以得到以下关系:M1 + M2 + M3 + M4 = M根据节点间的刚性关系,可以得到以下关系:k1 * (M2 - M1) = 0k2 * (M3 - M2) = 0k3 * (M4 - M3) = 0通过这些关系,我们可以求解出每个节点承载的力矩。


构造力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进展几何组成分析。
假设是具有多余约束的几何不变体系,那么需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-11=W2-1 9-W=2-3 3-W=2-4 2-W=2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
〔a〕〔b〕(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
〔a〕〔b〕(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定构造的弯矩图是否正确。
(a)(b)(c)(d)局部习题答案3-1〔a 〕m kN M B ⋅=80〔上侧受拉〕,kN F RQB 60=,kN F L QB 60-=〔b 〕m kN M A ⋅=20〔上侧受拉〕,m kN M B ⋅=40〔上侧受拉〕,kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c)4Fl M C =〔下侧受拉〕,θcos 2F F L QC =3-2 (a)0=E M ,m kN M F ⋅-=40〔上侧受拉〕,m kN M B ⋅-=120〔上侧受拉〕〔b 〕m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11〔下侧受拉〕〔c 〕m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10〔左侧受拉〕,m kN M DF ⋅=8〔上侧受拉〕,m kN M DE ⋅=20〔右侧受拉〕 3-4 m kN M BA ⋅=120〔左侧受拉〕3-5 m kN M F ⋅=40〔左侧受拉〕,m kN M DC ⋅=160〔上侧受拉〕,m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60〔右侧受拉〕,m kN M BD ⋅=45〔上侧受拉〕,kN F QBD 46.28=3-7 m kN M C ⋅=70下〔左侧受拉〕,m kN M DE ⋅=150〔上侧受拉〕,m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0〔上侧受拉〕,m kN M BA ⋅=36.0〔右侧受拉〕 3-9 m kN M AB ⋅=10〔左侧受拉〕,m kN M BC ⋅=10〔上侧受拉〕 3-10 〔a 〕错误 〔b 〕错误 〔c 〕错误 〔d 〕正确第4章 静定平面桁架和组合构造的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
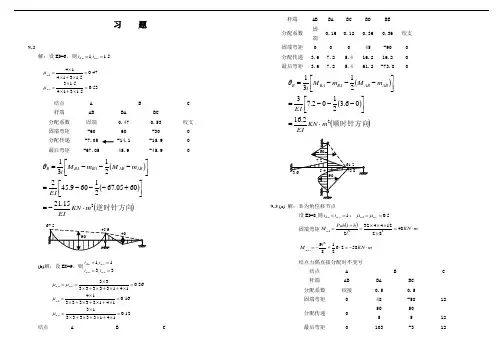
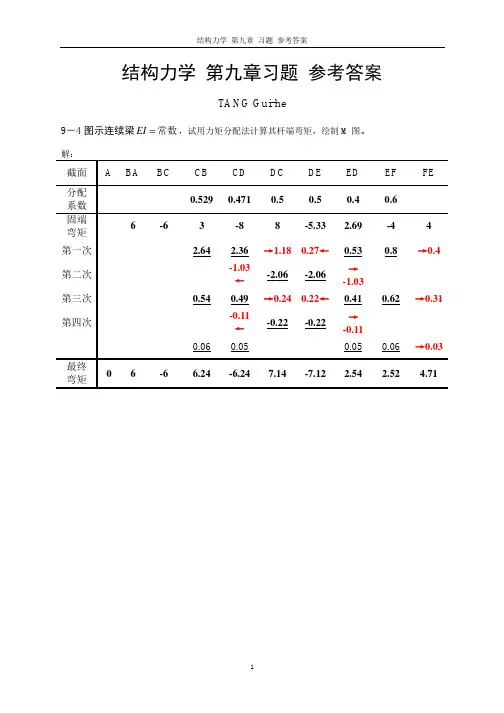
习 题9-2解:设EI=6,则5.1,1==BC AB i i 53.05.13145.1347.05.131414=⨯+⨯⨯==⨯+⨯⨯=BC BA μμ结点 A BC 杆端 AB BA BC 分配系数 固端 0.47 0.53 绞支 固端弯矩 -60 60 -30 0 分配传递 -7.05 -14.1 -15.9 0 最后弯矩-67.0545.9-45.9()()()逆时针方向215.216005.6721609.4522131m KN EI EI m M m M i AB AB BA BA B ⋅-=⎥⎦⎤⎢⎣⎡+---=⎥⎦⎤⎢⎣⎡---=θ(b)解:设EI=9,则3,31,1====BE BD BC AB i i i i12.0141333331316.0141333331436.01413333333=⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==BC BA BE BD μμμμ结点 A BC杆端 AB BA BC BD BE 分配系数 固端 0.16 0.12 0.36 0.36 绞支 固端弯矩0 45 -90 0 分配传递 3.6 7.2 5.4 16.216.20 最后弯矩 3.6 7.25.461.2 -73.8()()()顺时针方向22.1606.32102.732131m KN EI EI m M m M i AB AB BA BA B ⋅=⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡---=θ9-3 (a) 解:B为角位移节点设EI=8,则1==BC AB i i ,5.0==BC BA μμ 固端弯矩()m KN l b l Pab M BA ⋅=⨯⨯⨯⨯=+=4882124432222 m KN l M BC ⋅-=⋅+-=582621892 结点力偶直接分配时不变号结点 A BC 杆端 AB BA BC 分配系数 铰接 0.5 0.5 固端弯矩 0 48 -58 12 分配传递0 50 50 5 5 12 最后弯矩103-312(b) 解:存在B 、C 角位移结点设EI=6,则1===CD BC AB i i i73741413145.0141414==⨯+⨯⨯==⨯+⨯⨯==BC CB BC BA μμμμ固端弯矩:mKN M M M m KN M m KN M CDCB BC BA AB ⋅-=⨯+⨯-===⋅-=⋅-=14021808640080802结点 A BC杆端 AB BA BC CB CD 分配系数 固结 0.5 0.5 4/7 3/7 固端弯矩-80 80 0 0 -140 分配传递-20 -40 -40 -2047.5 91.4 68.6 -11.4 -22.8 -22.8 -11.4 3.25 6.5 4.9 -0.82-1.63-1.63-0.820.6 0.45 最后弯矩-112.2215.57-15.4866.28-66.05(c) 解:B 、C 为角位移结点51411,5441454414,51411=+==+==+==+=CD CBBC BA μμμμ固端弯矩:mKN M mKN M mKN M mKN M mKN M mKN M DC CD CB BC BA AB ⋅-=⨯-=⋅-=⨯-=⋅=⨯=⋅-=⨯-=⋅=⨯=⋅=⨯=10065242003524501252450125241283424646424222222结点 A BCD 杆端 AB BA BC CB CD 滑动 分配系数 滑动 0.2 0.8 0.8 0.2 -100固端弯矩64 128 -50 50 -200 分配传递15.6 -15.6 -62.4 -31.272.48 144.96 36.24 -36.24 14.5 -14.5 -58 -29 11.6 23.2 5.8 -5.8 2.32-2.32-9.28-4.643.7 0.93 -0.93 最后弯矩96.4295.58-95.6157.02-157.03-142.9796.42(d) 解:11313141413114131414145.0141414=⨯+⨯+⨯⨯===⨯+⨯+⨯⨯===⨯+⨯⨯=DBDE DCCD CA μμμμμ 固端弯矩:mKN M mKN M ED DE ⋅=⋅-=⨯-=383812422 结点 A CD E 杆端 AC CA CD DC DB DE ED 分配系数 固结 0.5 0.5 4/11 3/11 4/11 固结 固端弯矩0 0 0 0 0 -2.67 2.67 分配传递-5 -10 -10 -546/33 92/33 69/33 92/33 46/33 -0.35 - 23/33- 23/33-0.35 0.127 0.096 0.127 0.064 最后弯矩-5.35-10.7-9.3-2.442.190.254.12(e) 解:当D 发生单位转角时:()()2414-=⨯⨯=m EI K Y C 则())假设12(441==⨯=-m EI EIM DC73,74,3716,379,371216,12,16,9,12=====∴=====∴EB ED DE DA DC DE EB DE DA DC S S S S S μμμμμ 结点D EB 杆端 DC DA DE ED EB BE 分配系数 12/37 9/37 16/37 4/7 3/7 固结 固端弯矩0 0 -9 9 0 0 分配传递-2.57 -5.14 -3.86 -1.93 3.75 2.81 5 -2.5 -0.72 -1.43 -1.07 -0.54 0.230.18 0.31 0.16 最后弯矩3.982.99-6.985-5-2.47(f) 解:截取对称结构为研究对象。

结构力学——力矩分配法结构力学是研究物体在外力作用下的变形和破坏行为的学科。
其中,力矩分配法是一种求解结构梁的内力和变形的常用方法之一、本文将介绍力矩分配法的基本理论和应用。
首先,对于结构力学的研究,我们需要了解一些基本概念。
力矩是由力的作用点与旋转轴之间的距离和力的大小决定的。
在结构力学中,我们通常考虑作用在梁上的力和力矩。
梁是一种常见的结构元件,可以将其看作是在两个固定点之间作用的力的集合。
在力矩分配法中,我们将梁分割成若干个小段,然后逐段计算每个小段的内力和变形。
假设有一根长度为L,截面形状均匀的梁,并且在两个固定点之间施加了一系列分布力。
我们可以将梁分割成n个小段,每个小段的长度为Δx=L/n。
接下来,我们需要计算每个小段的内力和变形。
首先,我们可以根据材料力学的基本原理得出梁的拉伸、压缩和弯曲的力学方程。
然后,我们可以根据小段的切线方向和切线上的任意一点来推导出该小段的内力和弯曲方程。
最后,我们将内力分量在小段两端的力矩分配系数和位置矩分配系数进行合成,从而得出该小段的内力和弯曲方程。
在力矩分配法中,一个重要的概念是力矩分配系数。
力矩分配系数是一个无量纲的参数,用来表示力和力矩在小段两端分配的比例。
在计算力矩分配系数时,我们可以根据梁的几何形状和分布力的位置,利用力矩的基本原理进行推导。
力矩分配系数是力矩分配法的核心,它可以帮助我们计算出每个小段的内力和变形。
在实际应用中,力矩分配法通常用于求解多跨梁的内力和变形。
我们可以将多跨梁分割成若干个小段,并根据力矩分配法计算出每个小段的内力和变形。
然后,我们可以将各个小段的内力和变形进行叠加,得出整个多跨梁的内力和变形。
需要注意的是,力矩分配法具有一定的局限性。
首先,它只适用于存在弯曲变形的梁,对于其他类型的结构,如框架和板,需要采用其他的分析方法。
其次,力矩分配法仅适用于分布力作用在梁的直线部分上,对于弯曲部分或非均匀分布力的情况,需要采用其他的方法进行分析。
