9-3 单摆和复摆

单摆和复摆最本质的区别应该是摆动所绕的轴不一样（单摆是绕点），从而导致了一系列的差异，详述如下：单摆simplependulum质点振动系统的一种，是最简单的摆。

绕一个悬点来回摆动的物体，都称为摆，但其周期一般和物体的形状、大小及密度的分布有关。

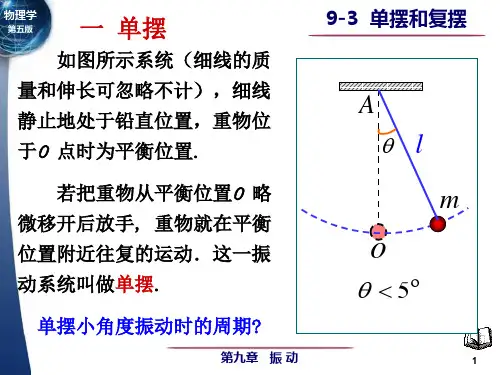
但若把尺寸很小的质块悬于一端固定的长度为l 且不能伸长的细绳上，把质块拉离平衡位置，使细绳和过悬点铅垂线所成角度小于5°，放手后质块往复振动，可视为质点的振动，其周期T只和l和当地的重力加速度g有关，即T=2π√(L/g)，而和质块的质量、形状和振幅的大小都无关系，其运动状态可用简谐振动公式表示，称为单摆或数学摆。

如果振动的角度大于5°，则振动的周期将随振幅的增加而变大，就不成为单摆了。

如摆球的尺寸相当大，绳的质量不能忽略，就成为复摆（物理摆），周期就和摆球的尺寸有关了。

伽利略第一个发现摆的振动的等时性，并用实验求得单摆的周期随长度的二次方根而变动。

惠更斯制成了第一个摆钟。

单摆不仅是准确测定时间的仪器也可用来测量重力加速度的变化。

惠更斯的同时代人天文学家J.里希尔曾将摆钟从巴黎带到南美洲法属圭亚那，发现每天慢2.5分钟，经过校准，回巴黎时又快2.5分钟。

惠更斯就断定这是由于地球自转引起的重力减弱。

I.牛顿则用单摆证明物体的重量总是和质量成正比的。

直到20世纪中叶，摆依然是重力测量的主要仪器。

复摆compoundpendulum在重力作用下，能绕通过自身某固定水平轴摆动的刚体。

又称物理摆。

复摆的转轴与过刚体质心C并垂直于转轴的平面的交点O称为支点或悬挂点。

摆动过程中，复摆只受重力和转轴的反作用力，而重力矩起着回复力矩的作用。

设质量为m的刚体绕转轴的转动惯量为I，支点至质心的距离为s，则复摆微幅振动的周期T=2π√(I/mgs)，式中g为重力加速度。

它相当于摆长l＝I／ms的单摆作微幅振动的周期。

在OC的延长线上取O′点使OO′＝l（l称等价摆长）则此点称为复摆的摆动中心。

单摆与复摆读书报告一、知识点简介绕一个悬点来回摆动的物体，都称为摆，其周期一般和物体的形状、大小及密度的分布有关。

但若把尺寸很小的质块悬于一端固定的长度为l且不能伸长的细绳上，把质块拉离平衡位置，使细绳和过悬点铅垂线所成角度小于︒5，放手后质块往复振动，可视为质点的振动，其周期T只和绳长l和当地的重力加速度g 有关，而与质块的质量、形状和振幅的大小都无关。

其运动状态可用简谐振动公式表示，称为单摆或数学摆。

如果振动的角度大于︒5，则摆不再做简谐振动，振动的周期将随振幅的增加而变大。

复摆是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系，又称物理摆。

复摆的周期与摆球的尺寸有关。

二、该知识点提出的背景摆与其性质是由伽利略发现并进行初步研究的。

在意大利的比萨城里，17岁的大学生伽利略在教堂时无意中观察到悬在天花板上的挂灯摆动逐渐平息的过程中，每次摆动所用的时间并不改变。

这一发现引起了伽利略的思考：是不是其他的摆动也跟吊灯相似，摆动一次的时间跟摆动幅度没关系？吊灯的轻重是否会影响摆动一次的时间？伽利略通过脉搏计时，数着吊灯的摆动次数。

吊灯的摆动幅度、摆动速度不同，但两次测量的时间是相同的。

回家后，他继续研究，发现并提出了单摆的等时性，即小角度振动的单摆的周期与质块的质量、形状和振幅无关，并通过实验求得单摆的周期随摆线长度的二次方根而变动。

在此基础上，荷兰数学家、物理学家惠更斯经过长期的研究,发现了单摆的周期规律,确定了单摆做简谐运动的周期公式,此公式为单摆做简谐运动时的周期T与摆长l、重力加速度g之间的定量关系。

如摆球的尺寸相当大，绳的质量不能忽略，在重力作用下，摆球为绕通过自身某固定水平轴摆动，视为刚体运动，当摆角不同时其运动方程的解也不同。

三、建立该知识点所经历的困难首先，伽利略实验所用的大小不同的木球、铁球、石块、铜球，体积都较大，并不能很好地视其为质点，且绳子与小球连接起来也有困难，对摆线的长度也有误差影响。

单摆复摆第四节单摆和复摆⼀、单摆1. 单摆、摆锤和摆线单摆⾓谐振动: 005<θ2. 动⼒学⽅程质量为m 的⼩球⽤细线悬挂，当球在⼩⾓度摆动时，则有：系统所受⼒矩：θmgl M sin -=由转动定律：βJ M =可得⾓加速度:θθβθsin sin 222lgml mgl J M dt d -=-===定义⾓频率:l g =ω，并注意到：θθ≈sin ，可得：0222=+θωθdt d （1）这就是单摆⾓谐振动所满⾜的动⼒学⽅程。

3. 运动学⽅程、周期⽅程（1）的解为：()?ωθθ+=t m cos ，最⼤摆⾓m θ和初相?由初始条件决定。

⽽且有：2020+=ωθθl v m ，=00θω?l v arctg 振动周期：g lT πωπ22==4. 应⽤：测量重⼒加速度，探矿等。

⼆、复摆任意形状的刚体悬挂后绕⼀固定轴O 作⼩⾓度摆动，质⼼到转轴距离为l ，则有：θθβθJmglJ mgl J M dt d -=-===sin 22为谐振动⽅程，相应的⾓频率:J mgl =ω，周期：mgl JT πωπ22==应⽤：测量转动惯量。

第五节简谐运动的能量⼀、能量表达式以在⽔平⾯上作简谐振动的弹簧振⼦为例，分析其能量变化，显然振⼦只受弹性⼒这⼀保守⼒作⽤，符合能量守恒。

设在任⼀时刻t ，振⼦位移为x ，速度为v ，注意到：x =A c o s (ωt +φ)，v =-ωA s i n (ωt +φ)，则其弹性势能E p 动能E K 分别为：动能: E k =m v 2/2=m ω2A 2s i n 2(ωt +φ)/2弹性势能: E p =k x 2/2=k A 2c o s 2(ωt +φ)/2= m ω2 A 2c o s 2(ωt +φ)/2 因此系统总机械能为：E =E k +E p = m ω2 A 2/2= k A 2/2 可见系统机械能守恒。

⼆、能量曲线注意理解能量守恒和动能、势能相互转化过程。