单摆复摆的区别
- 格式:doc
- 大小:22.50 KB
- 文档页数:2



八年级上册物理摆的知识点物理学中的摆,是指一个可旋转的物体由于其重心高于支点而能够转动。
它是一个非常简单且常见的物理现象,广泛应用于科学研究、日常生活和工业制造等领域。
本文将介绍八年级上册物理摆的知识点,包括摆的类型、运动规律、影响因素等方面。
希望本文能够帮助读者更好地理解物理学中的摆。
一、摆的类型摆可以分为单摆和复摆两种类型。
单摆,也称简谐摆,是一种由一根不可伸缩且质量趋近于0的细线挂着的质点,并在重力作用下做周期性运动的摆。
单摆的周期与摆长有关,与质点的质量、摆动幅度无关。
单摆常用于实验室中,可以用来测定重力加速度、验证万有引力定律等。
复摆,也称双摆或阿达木斯双摆,是由两个相互连接的单摆组成的系统。
复摆的周期与摆长、角度、质量等因素有关。
复摆的运动规律比单摆更加复杂,但它也可以用来研究能量转化、双星系统等领域的问题。
二、运动规律摆的运动规律可以用一个简洁的数学公式来描述。
对于单摆,其周期T与摆长L有关,可以用以下公式计算:T=2π√(L/g)其中,g为重力加速度,约为9.8m/s²。
这个公式说明,单摆的周期与摆长的平方根成正比,与重力加速度的平方根成反比。
对于复摆,其周期T既与摆长L有关,也与两个单摆的振动频率ω有关,可以用以下公式计算:T=2π√(L/g)/(2sin(θ/2))*π)其中,θ为两个单摆的夹角。
这个公式说明,复摆的周期与摆长成正比,与两个单摆的振动频率有关,与夹角的正弦函数成反比。
三、影响因素除了摆的类型和运动规律,还有一些因素会影响摆的运动。
首先是摆长,它是摆周期的关键因素。
摆长越长,周期越长;摆长越短,周期越短。
其次是重力加速度,它是摆周期的影响因素之一。
重力加速度越大,周期越短;重力加速度越小,周期越长。
还有一些影响因素体现在复摆的运动中。
复摆的两个单摆之间的距离和夹角不同,会导致复摆的周期变化。
如果夹角大于某个阈值,双摆运动将不再稳定。
四、应用领域摆在科学研究、日常生活和工业制造等领域有着广泛的应用。



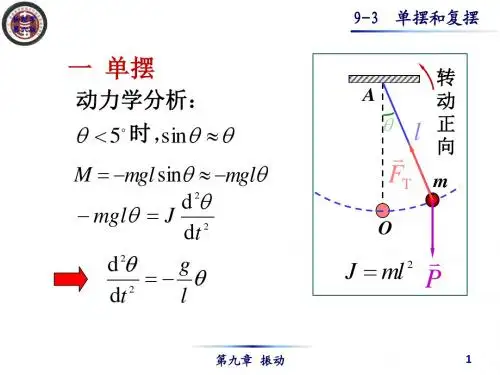

单摆复摆第四节单摆和复摆⼀、单摆1. 单摆、摆锤和摆线单摆⾓谐振动: 005<θ2. 动⼒学⽅程质量为m 的⼩球⽤细线悬挂,当球在⼩⾓度摆动时,则有:系统所受⼒矩:θmgl M sin -=由转动定律:βJ M =可得⾓加速度:θθβθsin sin 222lgml mgl J M dt d -=-===定义⾓频率:l g =ω,并注意到:θθ≈sin ,可得:0222=+θωθdt d (1)这就是单摆⾓谐振动所满⾜的动⼒学⽅程。
3. 运动学⽅程、周期⽅程(1)的解为:()?ωθθ+=t m cos ,最⼤摆⾓m θ和初相?由初始条件决定。
⽽且有:2020+=ωθθl v m ,=00θω?l v arctg 振动周期:g lT πωπ22==4. 应⽤:测量重⼒加速度,探矿等。
⼆、复摆任意形状的刚体悬挂后绕⼀固定轴O 作⼩⾓度摆动,质⼼到转轴距离为l ,则有:θθβθJmglJ mgl J M dt d -=-===sin 22为谐振动⽅程,相应的⾓频率:J mgl =ω,周期:mgl JT πωπ22==应⽤:测量转动惯量。
第五节简谐运动的能量⼀、能量表达式以在⽔平⾯上作简谐振动的弹簧振⼦为例,分析其能量变化,显然振⼦只受弹性⼒这⼀保守⼒作⽤,符合能量守恒。
设在任⼀时刻t ,振⼦位移为x ,速度为v ,注意到:x =A c o s (ωt +φ),v =-ωA s i n (ωt +φ),则其弹性势能E p 动能E K 分别为:动能: E k =m v 2/2=m ω2A 2s i n 2(ωt +φ)/2弹性势能: E p =k x 2/2=k A 2c o s 2(ωt +φ)/2= m ω2 A 2c o s 2(ωt +φ)/2 因此系统总机械能为:E =E k +E p = m ω2 A 2/2= k A 2/2 可见系统机械能守恒。
⼆、能量曲线注意理解能量守恒和动能、势能相互转化过程。



《单摆和复摆》课件一、教学内容二、教学目标1. 让学生了解单摆和复摆的定义、特点和运动规律。
2. 培养学生观察、实验、分析问题的能力。
3. 培养学生的团队合作精神,提高学生的实践操作能力。
三、教学难点与重点重点:单摆和复摆的运动规律。
难点:理解并掌握单摆和复摆的运动规律。
四、教具与学具准备教具:讲义、PPT、实验器材(包括单摆和复摆模型、计时器等)。
学具:笔记本、笔、实验报告表格。
五、教学过程1. 引入:通过展示单摆和复摆的模型,引导学生思考单摆和复摆的定义和特点。
2. 讲解:讲解单摆和复摆的定义、特点和运动规律,结合PPT和实验器材进行讲解。
3. 实验:让学生分组进行实验,观察并记录单摆和复摆的运动规律。
5. 练习:让学生运用所学的知识,解决一些实际问题。
六、板书设计板书设计如下:单摆和复摆2. 特点:单摆和复摆的摆动都是周期性的。
3. 运动规律:单摆和复摆的摆动规律与摆长、重力加速度等因素有关。
七、作业设计1. 请用简洁的语言描述单摆和复摆的定义和特点。
答案:单摆和复摆的摆动规律与摆长、重力加速度等因素有关。
八、课后反思及拓展延伸课后反思:本节课通过讲解和实验,让学生了解了单摆和复摆的定义、特点和运动规律。
但在实验环节,部分学生对实验操作不熟悉,需要在课后加强实验操作的培训。
拓展延伸:让学生进一步研究单摆和复摆的其他运动规律,如摆长、重力加速度等因素对摆动规律的影响。
重点和难点解析一、教学内容二、教学目标1. 让学生了解单摆和复摆的定义、特点和运动规律。
2. 培养学生观察、实验、分析问题的能力。
3. 培养学生的团队合作精神,提高学生的实践操作能力。
三、教学难点与重点重点:单摆和复摆的运动规律。
难点:理解并掌握单摆和复摆的运动规律。
四、教具与学具准备教具:讲义、PPT、实验器材(包括单摆和复摆模型、计时器等)。
学具:笔记本、笔、实验报告表格。
五、教学过程1. 引入:通过展示单摆和复摆的模型,引导学生思考单摆和复摆的定义和特点。
毕业论文题目名称:分别用单摆和复摆测量本地重力加速度的对比研究题目类型:研究论文学生姓名:王新霞院(系):物理与光电工程学院专业班级:物理11001班指导教师:程庆华辅导教师:程庆华时间:2014年1月至2014年6月目录毕业设计(论文)任务书 (I)毕业设计开题报告 (III)长江大学毕业论文(设计)指导教师审查意见 (IX)长江大学毕业论文(设计)评阅教师评语 (X)长江大学毕业论文(设计)答辩会议记录 (XI)中文摘要 (XII)外文摘要 (XIII)1.前言 (1)1.1问题的提出及研究意义 (1)1.2国内外研究现状 (2)1.3本文研究的目的及内容 (2)2.单摆 (3)2.1单摆测量重力加速度原理 (3)2.2单摆测量重力加速度实验 (4)3.复摆 (5)3.1复摆简介 (5)3.2复摆的制作 (5)3.3用三线摆测量复摆的转动惯量 (6)3.4复摆测量重力加速度原理 (10)3.5复摆测量重力加速度实验 (11)4.单摆和复摆测量本地重力加速度的对比 (12)4.1单摆复摆测量重力加速度原理对比 (12)4.2单摆复摆测量重力加速度制作难易程度对比 (13)4.3单摆复摆测量重力加速度操作难易程度对比 (14)4.4单摆复摆测量重力加速度精确程度对比 (14)5.结论 (15)6.参考文献 (15)致谢 (17)长江大学毕业设计(论文)任务书学院(系)物理与光电工程学院专业物理学班级物理1001班学生姓名王新霞指导教师/职称程庆华教授1.毕业设计(论文)题目:分别用单摆复摆测量当地重力加速度的对比研究2.毕业设计(论文)起止时间:2014年1 月~2014年6 月3. 毕业设计(论文)所需资料及原始数据(指导教师选定部分)[1]周衍柏.理论力学教程[M]. 第三版.北京:高等教育出版社,2009.7:116~160[2]扬长铭,田永红,王阳恩,程庆华. 物理实验[M]. 武汉:武汉大学出版社,2010.9:60~66[3]唐贵平,李西南,何兴.单摆实验法测量重力加速度的修正[J].中国教育技术装备,2002,(8):21~22[4]石承刚.“单摆测当地重力加速度实验浅析”[J].中学生数理化(高二版),2011,(Z1):63~64[5]李本苍,魏生贤,李会. 重力加速度测量方法的比较研究[J].科技世界,2013,(35):173~174[6]徐军华,徐兰珍,王树林.刚体转动惯量的一种新型测量法——复摆法[J].西安邮电学院学报. 2004,(3):93~94[7]张强.重力加速度的测量[J]. 曲靖师范学院学报. 1989,(03):43~44[8]李敏.用等效法研究摆动周期[J]. 数理化学习. 2008,(11):57~58[9]齐洪波.单摆振动中的等效问题[J]. 山西教育(招生考试). 2007,(01):33~34[10]吴巧云. 物理实验选择题三则[J]. 第二课堂(高中版). 2004,(01) :44~45[11]罗玉斌.单摆的周期公式[J]. 广东教育(综合版). 2006(02) :55~56[12]李传亮.用单摆测定重力加速度实验中的几点探讨[J]. 物理实验. 2006,(04) :43~44[13]易德文,盛忠志.利用单摆测重力加速度时的最大摆角的再讨论[J]. 物理实验. 2003,(07) :54~55[14]孙卫真.单摆法测重力加速度实验误差分析[J]. 贵州大学学报(自然科学版). 2003,(03) :26~27[15]郝建明,李咏波,和伟.单摆法测重力加速度的修正公式分析[J]. 云南师范大学学报(自然科学版). 2004,(03):34~35[16]陈涨涨,郑崇伟.单摆测重力加速度的研究[J]. 温州师范学院学报(自然科学版). 2002,(03) :45~46[17]郭文香.单摆测重力加速度误差分析[J]. 张家口师专学报. 2000,(02):34~35[18]金建伟.用单摆测重力加速度的改进[J]. 技术物理教学. 2003,(03):59~60[19]谷肖甬.减小单摆测重力加速度误差的方法[J]. 技术物理教学. 2005,(03):137~138[20]张海军.测量重力加速度的五种方法[J]. 中学物理教学参考. 2012,(4):24~25[21]刘华. 单摆复摆在不同摆角情形下的特性分析[J].科技创业月刊.2013,(2):139~1404.毕业设计(论文)应完成的主要内容(1)合理设计几个复摆;(2)利用三线摆测量物体转动惯量的原理测量复摆的转动惯量;(3)分别用单摆和复摆测量当地重力加速度;(4)通过实验,对单摆和复摆测量本地加速的方法及测量的精确程度进行对比分析并提出改进的方法。
单摆和复摆最本质的区别应该是摆动所绕的轴不一样(单摆是绕点),从而导致了一系列的差异,详述如下:
单摆
simplependulum
质点振动系统的一种,是最简单的摆。
绕一个悬点来回摆动的物体,都称为摆,但其周期一般和物体的形状、大小及密度的分布有关。
但若把尺寸很小的质块悬于一端固定的长度为l 且不能伸长的细绳上,把质块拉离平衡位置,使细绳和过悬点铅垂线所成角度小于5°,放手后质块往复振动,可视为质点的振动,其周期T只和l和当地的重力加速度g有关,即T=2π√(L/g),而和质块的质量、形状和振幅的大小都无关系,其运动状态可用简谐振动公式表示,称为单摆或数学摆。
如果振动的角度大于5°,则振动的周期将随振幅的增加而变大,就不成为单摆了。
如摆球的尺寸相当大,绳的质量不能忽略,就成为复摆(物理摆),周期就和摆球的尺寸有关了。
伽利略第一个发现摆的振动的等时性,并用实验求得单摆的周期随长度的二次方根而变动。
惠更斯制成了第一个摆钟。
单摆不仅是准确测定时间的仪器也可用来测量重力加速度的变化。
惠更斯的同时代人天文学家J.里希尔曾将摆钟从巴黎带到南美洲法属圭亚那,发现每天慢2.5分钟,经过校准,回巴黎时又快2.5分钟。
惠更斯就断定这是由于地球自转引起的重力减弱。
I.牛顿则用单摆证明物体的重量总是和质量成正比的。
直到20世纪中叶,摆依然是重力测量的主要仪器。
复摆
compoundpendulum
在重力作用下,能绕通过自身某固定水平轴摆动的刚体。
又称物理摆。
复摆的转轴与过刚体质心C并垂直于转轴的平面的交点O称为支点或悬挂点。
摆动过程中,复摆只受重力和转轴的反作用力,而重力矩起着回复力矩的作用。
设质量为m的刚体绕转轴的转动惯量为I,支点至质心的距离为s,则复摆微幅振动的周期T=2π√(I/mgs),式中g为重力加速度。
它相当于摆长l=I/ms的单摆作微幅振动的周期。
在OC的延长线上取O′点使OO′=l(l称等价摆长)则此点称为复摆的摆动中心。
支点和摆动中心可互换位置而不改变复摆的周期。
知道T和l,就可由周期公式求出重力加速度g。
当复摆受到一个冲量作用时,会在支点上引起碰撞反力。
若转轴是刚体对支点的惯量主轴,外冲量垂直于支点和质心的连线OC且作用于摆动中心O′上,则支点上的碰撞反力为零。
因此,复摆的摆动中心又称撞击中心。
机器中有些必须经受碰撞的转动件,如离合器、冲击摆锤等,为防止巨大瞬时力对轴承的危害,应使碰撞冲击力通过撞击中心。
转动惯量
momentofinertia
刚体绕轴转动惯性的度量。
其数值为I=(求和符号)Δmiri^2或I=(积分符号)ri^2dm,式中ri为组成刚体的质量微元Δmi(或dm)到转轴的垂直距离;求和号(或积分号)遍及整个刚体。
转动惯量只决定于刚体的形状、质量分布和转轴的位置,而同刚体绕轴的转动状态(如角速度的大小)无关。
规则形状的均质刚体,其转动惯量可直接计得。
不规则刚体或非均质刚体的转动惯量,一般用实验法测定。
转动惯量应用于刚体各种运动的动力学计算中。
描述刚体绕互相平行诸转轴的转动惯量之间的关系,有如下的平行轴定理:刚体对一轴的转动惯量,等于该刚体对同此轴平行并通过质心之轴的转动惯量加上该刚体的质量同两轴间距离平方的乘积。
由于和式的第二项恒大于零,因此刚体绕过质量中心之轴的转动惯量是绕该束平行轴诸转动惯量中的最小者。
刚体对一轴的转动惯量,可折算成质量等于刚体质量的单个质点对该轴所形成的转动惯量。
由此折算所得的质点到转轴的距离,称为刚体绕该轴的回转半径κ,其公式为κ=√I/M,式中M为刚体质量;I为转动惯量。
转动惯量的量纲为L2M,在SI单位制中,它的单位是kg·m2。
刚体绕某一点转动的惯性由更普遍的惯量张量描述。
惯量张量是二阶对称张量,它完整地刻画出刚体绕通过该点任一轴的转动惯量的大小。