附录Ⅰ常见截面的几何性质PPT课件

第七章

平面图形的几何性质

研究截面几何性质的意义

从上章介绍的应力和变形的计算公式中可以看出，应力

和变形不仅与杆的内力有关，而且与杆件截面的横截面面积

A、极惯性矩IP、抗扭截面系数WP等一些几何量密切相关。

因此要研究构件的的承载能力或应力，就必须掌握截面几何

性质的计算方法。

另一方面，掌握截面的几何性质的变化规律，就能灵活

机动地为各种构件选取合理的截面形状和尺寸，使构件各部

分的材料能够比较充分地发挥作用，尽可能地做到“物尽其

用”，合理地解决好构件的安全与经济这一对矛盾。

截面的几何性质 第一节 静矩

一、静距的概念

AySzddAzSydd





AAyyAAzz

AzSSAySS

dddd

z y dA

y z 静距是面积与它到轴的距离之积。

平面图形的静矩是对一定的坐标而言的，同一平面图形对不同的坐标轴，其静矩显然不同。静矩的数值可能为正，可能为负，也可能等于零。它常用单位是m3或mm3。

截面的几何性质

形心

d

A

z y

y z Cx

Cy



AyAyAzAz

CC







AydAyAzdAz

ACAC





ASyASz

zCyC



CyCzzASyAS

平面图形对z轴（或y轴

）的静矩，等于该图形面积

A与其形心坐标yC（或zC）

的乘积。

截面的几何性质

当坐标轴通过平面图形的形心时，其静矩为零；反

之，若平面图形对某轴的静矩为零，则该轴必通过平面

图形的形心。

如果平面图形具有对称轴，对称轴必然是平面图形

的形心轴，故平面图形对其对称轴的静矩必等于零。



CyCzzASyA

S截面的几何性质

二、组合图形的静矩

根据平面图形静矩的定义，组合图形对z轴（或y轴）的静

矩等于各简单图形对同一轴静矩的代数和，即







n

iCiiCnnCCyn

iCiiCnnCCz

zAzAzAzASyAyAyAyAS

截面图形的几何性质

一.重点及难点：

(一).截面静矩和形心

1.静矩的定义式

如图1所示任意有限平面图形，取其单元如面积，定义它对任意轴的

一次矩为它对该轴的静矩，即 y dA

ydAdSxxdAdS

y

==

x dA

整个图形对y、z轴的静矩分别为 x ×C y

∫∫

==

AAy

ydASxxdAS

（I-1） 0 A y x

2.形心与静矩关系 图I-1

设平面图形形心C的坐标为 则 0

CCzy,

AS

yx= ，

AS

xy= （I-2）

推论1 如果y轴通过形心（即0=x），则静矩0=

yS；同理，如果x轴

通过形心（即0=y），则静矩0=Sx；反之也成立。

推论2 如果x、y轴均为图形的对称轴，则其交点即为图形形心；如果

y轴为图形对称轴，则图形形心必在此轴上。

3.组合图形的静矩和形心

设截面图形由几个面积分别为

nAAAA……

321,,的简单图形组成，且一直

各族图形的形心坐标分别为……

332211,,,yxyxyx；；，则图形对y轴和x轴

的静矩分别为

∑∑∑∑

====

====

n

in

iiixixn

iiin

iyiy

yASSxAS

1111S

（I-3） 截面图形的形心坐标为

∑∑

===

n

iin

iii

AxA

x

11 ，

∑∑

===

n

iin

iii

AyA

y

11 （I-4）

4.静矩的特征

(1) 界面图形的静矩是对某一坐标轴所定义的，故静矩与坐标轴有关。

(2) 静矩有的单位为。 3m

(3) 静矩的数值可正可负，也可为零。图形对任意形心轴的静矩必定

为零，反之，若图形对某一轴的静矩为零，则该轴必通过图形的形心。

(4) 若已知图形的形心坐标。则可由式（I-1）求图形对坐标轴的静矩。

若已知图形对坐标轴的静矩，则可由式（I-2）求图形的形心坐标。组

合图形的形心位置，通常是先由式（I-3）求出图形对某一坐标系的静

矩，然后由式（I-4）求出其形心坐标。

（二）.惯性矩 惯性积 惯性半径

1. 惯性矩

定义 设任意形状的截面图形的面积为A（图I-3），则图形对O点的极

如有你有帮助，请购买下载，谢谢！

213页 附录I 截面的几何性质

习 题

Ι.1 试求图示平面图形的形心位置，并计算平面图形对Z轴的静矩。(单位：m)

(a) (b)

题Ι.1图

解：（a）图形的面积为

对Z轴的静距为

形心坐标为

（b）图形的面积为

对Z轴的静距为

对Y轴的静距为

形心坐标为

Ι.2 在图示的对称倒T形截面中，10.3 mb,20.6 mb,10.5 mh20.14 mh。

(1) 求形心 C的位置；

(2) 求阴影部分对0z轴的静矩；

(3) 问0z轴以上部分的面积对0z轴的静矩与阴影部分对0z轴的静矩有何关系?

题Ι.2图

解：（1）图形的面积为

对Z轴的静距为

形心坐标为

（2）求阴影部分对0z轴的静距为

02223110.140.60.140.2750.140.30.2750.14210m22ziiSAy（3）0z轴以上部分的面积对0z轴的静矩与阴影部分对0z轴的静矩关系为：经过计算得出相等。

Ι.3 求图示三角形截面对过形心的0z轴(0z轴平行于底边)与1z轴的惯性矩。

题Ι.3图

解：用积分法，如图（a）所示，取微元dy，则

对1z轴的惯性矩为

对1z轴的静矩为

形心坐标为

由平行移轴公式12CZZCIIZA得

Ι.4 试求图示各平面图形对形心轴的惯性轴。

(a) (b)

题Ι.4图

解：（a）对1z的静距为 如有你有帮助，请购买下载，谢谢！

214页 形心的坐标为：

由平行移轴公式得

图（c）

（b）首先计算对1Z的静距以求的形心轴Z的惯性矩：

1.计算静距为

由此计算形心轴为132298744m63mm40100604ZiSyA

有平行移轴公式得

Ι.5 图示为一箱形截面，z轴过形心且平行于底边，求截面对z轴的惯性矩。

材料力学 附录Ⅰ截面的几何性质

随着材料科学的不断发展，材料力学成为研究材料内部结构和力学行为的重要学科之一。在材料力学中，研究截面的几何性质是必不可少的一部分。本文将着重介绍截面几何性质的相关知识，探讨其在材料力学中的应用。

一、截面的定义

截面是指在任意平面上与某个物体相交的部分，一般用于描述杆件、梁、板等结构物体的断面形态。材料力学中，截面的几何参数是研究杆件、梁、板等结构物体受力行为的重要基础。

二、常见截面形状和特征

常见的截面形状包括矩形、圆形、三角形、梯形、T形等。其几何参数如截面面积、惯性矩、位置矩、受压、受弯等，均是描述结构物体受力行为的重要指标。

对于矩形截面来说，其惯性矩最大的方向是短边方向，即截面中心距离短边较远的一侧。圆形截面的惯性矩与位置矩均与截面对称轴有关。对于三角形截面来说，其惯性矩与位置矩也是与截面对称轴有关的，而梯形截面和T形截面的惯性矩和位置矩则需要具体计算得出。

三、截面的常见计算公式

在计算截面的几何性质时，需要用到一些公式。以下是一些常见的公式：

1、截面面积

截面面积是截面内部曲线及其间距离所组成的面积。不同截面形状的截面面积计算公式如下：

矩形截面：A = bh

圆形截面：A = πr²

三角形截面：A = 1/2bh

梯形截面：A = 1/2(a+b)h

T形截面：A = (bh₁+ (b₂-h₂)h₂/2)

2、截面惯性矩

截面惯性矩是描述结构物体受弯作用时截面抵抗弯曲的能力的重要参数，其计算公式如下：

Ixx = ∫(y²)dA

Iyy = ∫(x²)dA

其中，x，y分别表示离截面中心最远的两侧点的坐标，dA表示一个面积微元。

3、位置矩

位置矩是描述结构物体受纵向荷载作用时截面的抵抗能力的参数，其计算公式如下：

Qx = ∫(y)dA

Qy = ∫(x)dA

其中，x，y分别表示离截面中心最远的两侧点的坐标，dA表示一个面积微元。

四、截面几何性质在材料力学中的应用

立体几何中的 截面问题

本文档旨在介绍立体几何中的截面问题，包括截面的定义、性质、计算方法等方面的内容。通过对截面问题的介绍和详细解析，读者可以更好地理解和应用相关知识。

1、截面的定义

在立体几何中，截面是指一个平面和立体图形相交而形成的曲线或平面部分。截面可以是二维的曲线，也可以是三维的平面。截面问题主要研究在不同情况下的截面形状、面积、体积等性质。

2、截面的性质

截面的性质取决于所截图形的性质以及截面的位置和方向。主要包括以下几个方面：

2.1 几何形状：截面可以是点、线段、圆、椭圆、抛物线等各种几何形状。

2.2 面积：截面的面积可能是有限的，也可能是无限的。

2.3 体积：截面可以用来计算图形的体积，从而解决与立体几何有关的问题。

2.4 位置和方向：不同位置和方向的截面可以得到不同的结果，需要根据具体问题进行分析和计算。 3、截面的计算方法

根据截面的性质和具体问题的要求，有多种不同的计算方法可以用来求解截面问题。常用的计算方法包括以下几种：

3.1 几何分析法：通过几何分析截面的形状和性质，利用几何定理和方法计算截面的面积、体积等。

3.2 数学建模法：将截面问题转化为数学模型，利用数学方法和计算机技术进行计算和求解。

3.3 数值模拟法：通过数值模拟和计算机仿真，模拟和计算截面问题的解答。

3.4 实验测量法：通过实际测量和实验，获取截面的相关数据和性质进行计算和分析。

附件：

本文档无附件。

法律名词及注释：

1、立体几何：研究三维空间中点、线、面等几何图形的性质和变换的数学学科。

2、截面：一个平面和立体图形相交而形成的曲线或平面部分。

第7章 截面图形的几何性质

教学提示：在对构件进行应力和强度等计算时，需要用到构件截面图形的几何性质，

即与构件截面几何形状和尺寸有关的一些量，例如形心、静矩、惯性矩、惯性半径、极惯

性矩、惯性积等。本章的主要内容就是讨论这些几何性质的定义和计算。

教学要求：通过本章学习，要求理解形心、静矩、惯性矩、极惯性矩、惯性积和主惯

性矩的概念，会用平行移轴公式计算组合截面对形心轴的惯性矩、主惯性矩等。

受力构件的承载能力，不仅与材料性能和加载方式有关，而且与构件截面的几何形状

和尺寸有关。当研究构件的强度、刚度和稳定性问题时，都要涉及到一些与截面形状和尺

寸有关的几何量。这些几何量包括：形心、静矩、惯性矩、惯性半径、极惯性矩、惯性积、

主惯性矩等，统称为“截面图形的几何性质”。研究这些几何性质时，完全不需考虑研究

对象的物理和力学因素，只作为纯几何问题处理。

7.1 静矩与形心

考察如图7.1所示任意截面几何图形。在其上取面积微元dA，设该微元在Oyz坐标系

中的坐标为(y、z)。定义下列积分

d

yASzA=∫

， d

z

ASyA=∫

(7.1)

图7.1

分别为截面图形对y轴和z轴的静矩(或称为面积矩)。其量纲为长度的三次方。常用单

位是3

m或3

mm。

由于均质等厚薄板的重心与薄板截面图形的形心有相同的坐标(

Cy、

Cz)，而薄板的重

心坐标由式(2.24)给出，即

dd

AAz

CyVyA

S

y

VAA===∫∫

dd

y

AA

CzVzA

S

z

VAA===∫∫

第7章 截面图形的几何性质

·91·

·91

· 所以，形心坐标为

d

Az

CyA

S

y

AA==∫

， d

y

A

CzA

S

z

AA==∫

(7.2a)

或

yCSAz=⋅，

zCSAy=⋅ (7.2b)

由式(7.2)可知，若某坐标轴通过形心轴，则图形对该轴的静矩等于零，即若0

Cy=，

则0

zS=，或若0

Cz=，则0

yS=；反之，若图形对某一坐标轴的静矩等于零，则该坐标轴

必然通过图形的形心。静矩与所选坐标轴有关，其值可能为正、负或零。

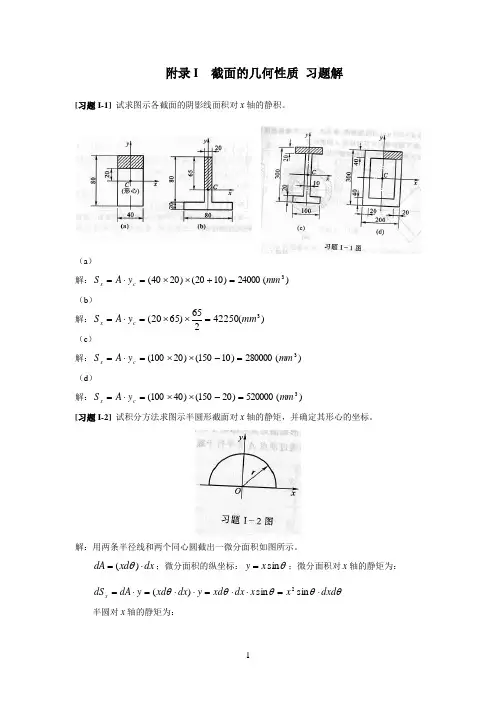
1 附录I 截面的几何性质 习题解

[习题I-1] 试求图示各截面的阴影线面积对x轴的静积。

（a）

解：)(24000)1020()2040(3mmyAScx

（b）

解：)(42250265)6520(3mmyAScx

（c）

解：)(280000)10150()20100(3mmyAScx

（d）

解：)(520000)20150()40100(3mmyAScx

[习题I-2] 试积分方法求图示半圆形截面对x轴的静矩，并确定其形心的坐标。

解：用两条半径线和两个同心圆截出一微分面积如图所示。

dxxddA)(；微分面积的纵坐标：sinxy；微分面积对x轴的静矩为：

dxdxxdxxdydxxdydAdSxsinsin)(2

半圆对x轴的静矩为：

2 32)]0cos(cos[3]cos[]3[sin33003002rrxddxxSrrx

因为cxyAS，所以cyrr232132 34ryc

[习题I-3] 试确定图示各图形的形心位置。

（a）

解：

习题I-3(a): 求门形截面的形心位置

矩形 Li Bi Ai Yci AiYci Yc 离顶边

上 400 20 8000 160 1280000

左 150 20 3000 75 225000

右 150 20 3000 75 225000

14000 1730000 123.6 46.4

Ai=Li*Bi Yc=∑AiYci/∑Ai

(b)

解：

习题I-3(b): 求L形截面的形心位置

矩形 Li Bi Ai Yci AiYci Yc Xci

AiXci Xc

下 160 10 1600 5 8000 80 128000

左 90 10 900 55 49500 5 4500

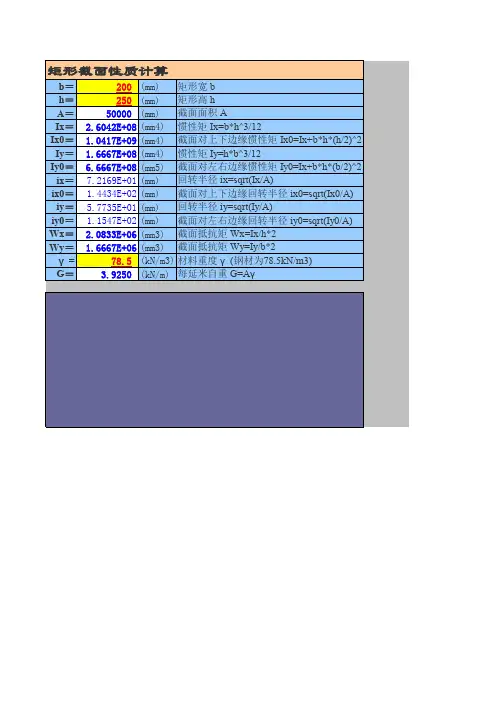
b＝200(mm)矩形宽 bh＝250(mm)矩形高 hA＝50000(mm)截面面积 AIx＝2.6042E+08(mm4)惯性矩 Ix=b*h^3/12Ix0＝1.0417E+09(mm4)截面对上下边缘惯性矩 Ix0=Ix+b*h*(h/2)^2Iy＝1.6667E+08(mm4)惯性矩 Iy=h*b^3/12Iy0＝6.6667E+08(mm5)截面对左右边缘惯性矩 Iy0=Ix+b*h*(b/2)^2ix＝7.2169E+01(mm)回转半径 ix=sqrt(Ix/A)ix0＝1.4434E+02(mm)截面对上下边缘回转半径 ix0=sqrt(Ix0/A)iy＝5.7735E+01(mm)回转半径 iy=sqrt(Iy/A)iy0＝1.1547E+02(mm)截面对左右边缘回转半径 iy0=sqrt(Iy0/A)Wx＝2.0833E+06(mm3)截面抵抗矩 Wx=Ix/h*2Wy＝1.6667E+06(mm3)截面抵抗矩 Wy=Iy/b*2γ=78.5(kN/m3)材料重度 γ(钢材为78.5kN/m3)G＝3.9250(kN/m)每延米自重 G=Aγ矩形截面性质计算

常用截面几何性质计算公式JX

1.矩形截面：

矩形截面是一种常见的结构截面形式。假设矩形截面宽度为b，高度为h，则其面积可以通过以下公式计算：

A=b*h

质心位置可以通过以下公式计算：

x=b/2

y=h/2

惯性矩可以通过以下公式计算：

Ix=(b*h^3)/12

Iy=(h*b^3)/12

截面模数可以通过以下公式计算：

Wx=(b*h^2)/6

Wy=(h*b^2)/6

2.圆形截面：

圆形截面是另一种常见的结构截面形式。假设圆形截面的半径为r，则其面积可以通过以下公式计算：

A=π*r^2

质心位置在圆心上，即x=0，y=0。 惯性矩可以通过以下公式计算：

Ix=(π*r^4)/4

Iy=(π*r^4)/4

截面模数可以通过以下公式计算：

Wx=(π*r^3)/4

Wy=(π*r^3)/4

3.等边三角形截面：

等边三角形截面是一个等边三角形形状的结构截面。假设等边三角形截面的边长为a，则其面积可以通过以下公式计算：

A = (sqrt(3) * a^2) / 4

质心位置可以通过以下公式计算：

x=a/2

y = (sqrt(3) * a) / 6

惯性矩可以通过以下公式计算：

Ix = (a^4 * sqrt(3)) / 48

Iy=(a^4)/48

截面模数可以通过以下公式计算：

Wx = (a^3 * sqrt(3)) / 12

Wy=(a^3)/12 以上是常见的几种截面几何性质的计算公式，通过这些公式可以方便地计算结构截面的重要性质，为结构设计和分析提供参考。在实际应用中，还需要根据具体的截面形状和尺寸选择相应的公式进行计算。

【陆工总结材料力学考试重点】之（第4章）

截面的几何性质

1、静矩与形心？

答：图形几何形状的中心称为形心。

对于图示的任意平面图形，任取一微元dA，设其坐标为（y，z），则定义：

平面图形对于z轴的静矩：𝑆

𝑧=∫𝑦𝑑𝐴

𝐴

平面图形对于y轴的静矩：𝑆

𝑦=∫𝑧𝑑𝐴

𝐴

定义平面图形对于坐标轴（y，z）的惯性积：𝐼

𝑦𝑧=∫𝑦𝑧𝑑𝐴

𝐴

根据积分的性质可知：当选取的y、z轴不一样时，则惯性积𝐼

𝑦𝑧也不一样。

若对于某对坐标轴𝑦

0、𝑧

0使得𝐼

𝑦0𝑧0=0，则该对坐标轴𝑦

0、𝑧

0称为主轴，过

形心的主轴称为形心主轴（注：求主轴非常麻烦，大家只需记住以下结论）。

结论：

1）圆截面的任何两条过圆心的且互相垂直的直径都是形心主轴；

2）矩形截面的两条对称轴就是形心主轴；

3）若截面有2跟对称轴，此两轴即为形心主轴，若截面只有一根对称轴，

则该轴必为形心主轴，令一形心主轴为通过形心且与该对称轴垂直的轴。

2、简单截面的惯性矩与极惯性矩？

答：

（1）惯性矩与极惯性矩的定义

如图，任意图形的面积为A，在其上任取微元dA，坐标为（y，z），则定义：

平面图形对于z轴的惯性矩为：𝐼

𝑧=∫𝑦2𝑑𝐴

𝐴

平面图形对于y轴的惯性矩为：𝐼

𝑦=∫𝑧2𝑑𝐴

𝐴

平面图形对坐标原点O点的极惯性矩为：𝐼

𝑝=∫𝜌2𝑑𝐴

𝐴

式中：𝜌为该微元dA到原点的距离，由图可知：𝑦2+𝑧2=𝜌2

则：𝐼

𝑝=𝐼

𝑦+𝐼

𝑧。

（2）常用截面的惯性矩和极惯性矩

①实心圆截面（注：直径为d，对于形心主轴（即y、z轴过圆心O））

𝐼

𝑝=𝜋𝑑432，又：𝐼

𝑝=𝐼

𝑦+𝐼

𝑧，故：𝐼

𝑦=𝐼

𝑧=𝜋𝑑464

②空心圆截面（注：外径为D，内径为d，空心比α=𝑑𝐷，对于形心主轴）

𝐼

𝑝=𝜋𝐷432（1−𝛼4），又：𝐼

𝑝=𝐼

T形截面—截面几何性质计算

T形截面通常用于横梁和柱子的设计中，具有较高的刚度和强度。在计算T形截面的几何性质时，可以考虑以下几个重要的参数：截面面积、惯性矩、抗剪面积和截面模量。

1.截面面积：

截面面积是指截面内所有的区域的面积之和，通常用A表示。对于T形截面，可以通过将上下两个矩形相加，再减去中间的矩形得到总面积。

2.惯性矩：

惯性矩是描述截面形状对于转动惯量的影响程度的物理量。对于T形截面，有两个惯性矩需要计算：x轴惯性矩和y轴惯性矩。x轴惯性矩（Ix）描述了围绕与截面的中心线平行于x轴旋转的转动惯量，y轴惯性矩（Iy）类似。可以通过将各个小区域的面积乘以它们到截面中心线的距离的平方再相加来计算这些惯性矩。

3.抗剪面积：

抗剪面积是指悬臂梁在受到剪力作用时，用于抵抗剪切变形的有效截面的面积。对于T形截面，可以通过将梁右边矩形的面积减去中间矩形的面积来计算剩余的抗剪面积。

4.截面模量：

截面模量是描述截面形状对于弯曲刚度的影响程度的物理量。对于T形截面，使用两个截面模量来描述其弯曲刚度：x轴截面模量（Sx）和y轴截面模量（Sy）。x轴截面模量描述了横截面围绕与截面的中心线平行于x轴弯曲时的刚度，y轴截面模量描述了类似情况下的刚度。截面模量可以通过将矩形和圆形的截面模量相加来计算。

此外，还可以计算T形截面的其他几何性质，如中心重心的位置和分割形心（距离两侧的边界的距离）。这些参数可以用于更详细的结构计算和分析。

在设计过程中，这些截面几何性质的计算是非常重要的，可以用于评估结构的刚度、强度和稳定性。它们也可以用于计算应力、应变和变形等细节参数，以便更好地了解和优化结构的性能。

常用截面图形的几何性质

1.矩形

坐标轴原点位于形心处

A=bh

Ixy = 0

2.矩形

 坐标轴原点位于角点处

3.三角形

坐标轴原点位于形心处

4.三角形

坐标轴原点位于角点处

5.梯形

坐标轴原点位于形心处

6.圆

坐标轴原点位于中心处

Ixy = 0

7.圆环

坐标轴原点位于中心处

Ixy = 0 8.半圆

坐标轴原点位于形心处

Ixy = 0

9.椭圆

坐标轴原点位于形心处

Ixy = 0

10.抛物线

11.抛物线外面积

坐标轴原点位于顶点处

符号： A = 面积； = 至形心C的距离； Ix,Iy = 对轴的惯性矩； Ix,Iy = 对轴的惯 J = Ix + Iy = 极惯性矩； IBB = 对 B-B 轴的惯性矩

史上最全的常用截面几何特性计算公式

构件截面的几何性质，如静力矩、形心、轴向惯性矩、极惯性矩、惯性积和主惯性轴位置等，对构件的承载能力有影响，常用于分析构件的弯曲、扭转和剪切。

1.静态力矩:也称为面积力矩或静态表面力矩。截面对轴线的静力矩等于每个微区的积分乘以整个截面上微区到轴线的距离。静力矩可以是正的，也可以是负的。它的维数是长度的三次方。静力矩的力学意义是:如果有均布载荷作用在截面上，其值表示为单位面积的量，则该载荷在某一轴上的合成力矩等于分布载荷乘以该轴的静力矩。

2、形心：又称面积中心或面积重心，是截面上具有如下性质的点：截面对通过此点任一个轴的静矩等于零。如果将截面看成一均质等厚板，则截面的形心就是板面的重心。形心坐标xo、yo的计算公式为：

3、惯性矩：反映截面抗弯特性的一个量，简称惯性矩。截面对某个轴的轴惯性矩等于截面上各微面积乘微面积到轴的距离的平方在整个截面上的积分。下图所示的面积为A的截面对x、y轴的轴惯性矩分别为：

转动惯量总是正的，量纲是长度的四次方。构件的抗弯能力与轴的惯性矩成正比。一些典型截面的轴惯性矩可在专业手册中找到。例如，平行四边形对中心线的惯性矩为

4、极惯性矩：反映截面抗扭特性的一个量。截面对某个点的极惯性矩等于截面上各微面积乘微面积到该点距离的平方在整个截面上的积分。下图所示面积为A的截面对某点O的极惯性矩为：

极惯性矩永远是正的，量纲是长度的四次方。构件的抗扭能力与惯性矩成正比。圆形截面相对于其中心的惯性矩为

5、惯性积：截面对于两个正交坐标轴的惯性积等于截面上各个微面积乘微面积到两个坐标轴的距离在整个截面上的积分。面积为A的截面对两个正交坐标轴x、y的惯性积为:

惯性积的量纲是长度的四次方。截面位于坐标系的一、三象限,Ixy为正，位于二、四象限则为负。

6.主惯性轴:使截面惯性积为零的一对正交坐标轴称为截面主惯性轴，简称主轴。截面对主惯性轴的惯性矩称为主惯性矩。若两条主惯性轴的交点为质心，则这两条轴称为质心主惯性轴(或称主质心惯性轴)。截面对它们的惯性矩称为质心主惯性矩(或主质心惯性矩)。

材 料 力 学

·

80

·第4章 截面·平面图形几何性质

计算杆件在外力作用下的应力和变形等，都要用到与杆件截面的几何形状及尺寸有关的

一些几何量。例如在轴向拉压的计算中所用到的横截面面积A，圆轴扭转计算中所用到的极

惯性矩IP和抗扭截面系数Wt。在后面的几章中还要涉及杆件横截面的形心、静矩、惯性

矩、惯性半径、惯性积、形心主轴及形心主惯性矩等，这些与材料的力学性质无关的几何量

统称为截面的几何性质。

4.1 截面图形·形心和静矩

4.1.1 形心和静矩

杆件的横截面是一个平面图形，现取任意平

面图形，设其面积为A，如图4.1所示。平面图形

的几何中心C称为形心。若将此平面图形视为均质

等厚的超薄板，由静力学可知，则该薄板重心、质

心和薄板图形的形心三者在oyz平面内重合。在yoz

坐标系中，取平面图形任意点（y，z）处微面积

dA，则该薄板的重心、质心、形心在yoz坐标系中

的坐标为

dd(Mg)(d)d

()()

dd(Mg)(d)d

()()c

cyWyyAgyA

y

WMgAgA

zWzzAgzA

z

WMgAgAρ

ρ

ρ

ρ⎫

⎪====

⎪

⇒⎬

⎪

====⎪

⎭∫∫∫∫

∫∫∫∫ d

dc

cyA

y

A

zA

z

A=

=∫

∫ （4.1）

式（4.1）即为计算平面图形形心C的坐标公式。其中的二个积分项写为

d

dyA

zASzA

SyA=

=∫

∫ （4.2）

式中，Sy、Sz分别定义为平面图形对于y轴和z轴的静矩（平面矩），也称为一次矩。

由式（4.1）和式（4.2）可以得出静矩与形心的关系式

z

cS

y

A= ， y

cS

z

A= （4.3a）

或

zcSAy=i ，

ycSAz=i （4.3b）

由式（4.1）～式（4.3）可以得出如下结论：

图4.1 任意横截面图形及形心和静矩的定义 第4章 截面·平面图形几何性质

·81·（1）截面的静矩是对某一坐标轴而言的，同一图形对不同坐标轴有不同的静矩，其值可

正，可负，也可为零。静矩的量纲为长度的三次方。

（2）若某一坐标轴通过平面图形的形心，则平面图形对该形心轴的静矩必等于零。反

附录I 截面的几何性质

1 习题

I−1 试求平面图形的形心位置。

解：由对称 m3.0cz

m357.02.04.04.02.02.06.07.02.04.04.04.02.01.02.06.0cy

解：m093.04.01.01.03.005.04.01.015.01.03.0cz

m193.04.01.01.03.03.04.01.005.01.03.0cy

I−2 试求平面图形的形心坐标。

解： y=zn y

z

l O

(c) 0.1 0.1 0.1 0.1 0.2 0.2 0.2

0.4

z y

O

(a)

0.1

0.1 0.4 0.2

z y

O

(b) 附录I 截面的几何性质

2 lnndzzzdzzzlnln2100c

200cnldzzydyylynlnlnn

解：由对称 rzc

3423222232022crrrrydyyryr

I−3 试求图示截面的阴影线面积对z轴的静矩。（图中C为截面形心）

解：3c**mm24000302040yASz

y

z

l O r

(d)

80 20 z y

40

(a)

C

80 80

20 65

z y 20

(b) C 附录I 截面的几何性质

3 解：3c**mm422505.322065yASz

I−4 求以下截面对z轴的惯性矩。（z轴通过截面形心）

解：64646442414241ddddIz

解：12121242414241aaaaIz

I−5 试求图示三角形截面对通过顶点A并平行于底边BC的z轴的惯性矩。

解：

4302bhybdyhyIhz

I−6 试求图示r=1m半圆形截面对于z轴的惯性矩。其中z轴与半圆形的底边平行，相距1m。

圆锥是一种几何图形，它具有一个圆形的底部和侧面的斜面，这使得它在空间中形成一个尖锐的顶点。在研究圆锥的性质时，我们常常会遇到许多有趣的问题，其中一个问题就是在经过圆锥顶点的截面中，轴截面的面积最大。

1. 圆锥的定义

圆锥是由一个圆形的底部和其上的一条或多条斜面组成的几何图形。在圆锥中，底部的圆被称为底面，而连接底面和顶点的线段被称为轴。如果圆锥的侧面是垂直于底面的，那么这个圆锥就是一个正圆锥；如果侧面不垂直于底面，那么这个圆锥就是一个斜圆锥。

2. 截面的概念

截面是指通过一个几何体切割得到的平面图形。在圆锥中，当一个平面通过圆锥的顶点时，圆锥被分割成两部分，而切割得到的图形就是圆锥的截面。

3. 轴截面的定义

轴截面是指通过圆锥的顶点，并且与圆锥轴平行的平面所得到的截面。轴截面的特殊性在于它们是通过圆锥的顶点的。在圆锥的研究中，轴截面具有重要的几何性质。

4. 轴截面的面积

在经过圆锥顶点的截面中，轴截面的面积最大是一个经典的几何问题。为了求解这个问题，我们需要利用一些几何知识和数学方法来进行推导和计算。

5. 问题分析

我们首先对问题进行分析。设圆锥的底面半径为R，轴截面的半径为r，圆锥的高度为H，截面与轴的距离为x。根据几何知识，我们可以得到轴截面的面积与截面半径r的平方成正比，即S=πr^2。而根据圆锥的性质，r和x满足以下关系：r/R=x/H。

6. 求解过程

接下来，我们通过数学方法来求解这个问题。根据上面的关系式，我们可以得到r和x的关系：r=xR/H。我们将r表示为x的函数，并代入轴截面的面积公式中，得到轴截面的面积与x的关系。

7. 最大值的求解

为了得到轴截面的面积最大值，我们需要求解这个关系式的极值。通过对轴截面的面积关于x进行求导，并令导数等于0，我们可以得到轴截面面积的最大值对应的x值。将这个x值代入轴截面面积的关系式中，就可以得到轴截面的最大面积。

8. 结论

经过推导和计算，我们得到了在经过圆锥顶点的截面中，轴截面的面积最大的结论。这个结论不仅具有理论意义，也有实际的应用意义，在工程和科学领域都有着重要的作用。