材料力学附录

材料力学(金忠谋)第六版答案-附录附录I 截面图形的几何性质I-1 求下列截面图形对z 轴的静矩与形心的位置。

解：（a ）)2)2((2)2(2h t h b t h ht t h bt s z ++=⋅++=hb h t h b h b t h t h b t A s y zc +++=+++==2)2()()2)2((22（b ）322332219211)}2)4()43()41()43(32(])4()43[(2{4442DD D D D D D D D D s z =--⨯-+⨯⨯-=ππDD D D D DAs y z c 1367.0])2()43[(2)44(219211223=-⨯+⨯==π（c ）]22)[(22)(2h t t b t h ht t t t b s z +⋅-=⨯+⨯⨯-=tb)(2)(2t b h h t t b A s y z c -++-==I-2 试求（1）图示工字形截面对形心轴 y 及 z 的惯性矩zI 与I y 。

（2）图示 T 字形截面对形心轴的惯矩zI 与I y 。

解(a)12)2)((12)2)((123333t h t b bh t h t b bh J z ---=---=12))2(2(12))(2(1222333t t h b t t t h tb J y -+=-+=(b) cmy c 643.9)520515(2)515(552522=⨯+⨯-⨯+⨯=(b433423231615121551252010186520)643.91025(12205515)5.2643.9(12515cm J cm J y z =⨯+⨯==⨯⨯--+⨯+⨯⋅-+⨯=I-3 求图示椭圆截面对长轴的惯矩、惯性半径与对形心的极惯矩。

解：θθcos ,sin ⋅=⋅=a z b yθθd b dy cos = ⎰⎰--⋅==∴b bbbz zdyy dA y J 222322223224cos sin 2cos cos sin 2ab d abd b a b J bb z πθθθθθθθππ==⋅=⎰⎰--)(4)(42422333b a ab b a ab J J J b ab ab AJ i y z p zz +=+=+====ππππI-4 试求图示的41的圆面积（半径a ）对于z ，yyy 轴的惯性积zyI 。

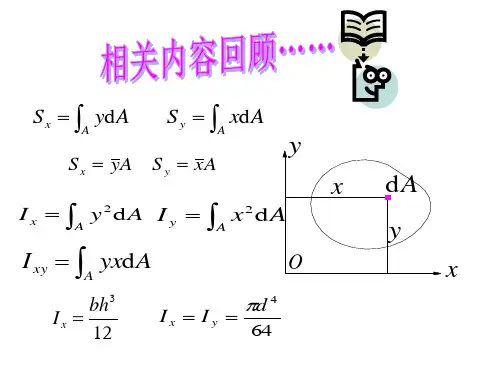
材料力学（土）笔记附录I 截面的几何性质1．截面的静矩和形心位置设任意形状的截面，其截面面积为A ，从截面中坐标为(,)x y 处取一面积元素dA 则xdA 和ydA 分别称为该面积元素dA 对于y 轴和x 轴的静矩或一次矩y AS xdA =⎰定义为该截面对y 轴的静矩x AS ydA =⎰定义为该截面对x 轴的静矩上述积分应遍及整个截面面积A截面的静矩是对一定的轴而言的，同一截面对不同坐标轴的静矩不同 静矩可能为正值也可能为负值，也可能等于零，常用单位为m ³或mm ³ 由理论力学可知，在Oxy 坐标系中，均质等厚度薄板的重心坐标为y AxdA S x AA==⎰，xAydA S y AA==⎰ 均质薄板的重心与该薄板平面图形的形心是重合的上式可计算形心坐标，在知道截面对y 轴和x 轴的静矩以后，即课的截面形心坐标 将上式改写为y S Ax =，x S Ay =则在已知截面的面积A 及其形心的坐标x 、y 时 就可求得截面对y 轴和x 轴的静矩，由上式可看出，截面对通过其形心的轴的静矩恒等于零反之，若截面对于某一轴的静矩等于零，则该轴必通过截面的形心当截面由若干简单图形组成时，由于简单图形的面积及其形心位置均为已知由静矩定义可知，截面各组成部分对某一轴的静矩之代数和等于该截面对同一轴的静矩 即得整个截面的静矩为1n y i i i S A x ==∑，1nx i i i S A y ==∑式中，i A 和i x 、i y 分别代表任一简单图形的面积及其形心的坐标n 为组成截面的简单图形个数可得组合截面的星系坐标为11ni ii nii A xx A===∑∑，11ni ii nii A yy A===∑∑2．极惯性矩·惯性矩·惯性积设一面积为A 的任意形状截面，从截面坐标为(,)x y 处取一面积元素dA 则dA 与其至坐标原点距离平方的乘积2dA ρ 称为面积元素对O 点的极惯性矩或截面二次极矩2p AI dA ρ=⎰定义为整个截面对O 点的极惯性矩上述积分应遍及整个截面面积A ，极惯性矩的数值恒为正，单位为4m 或4mm面积元素dA 与其至y 或x 轴距离平方的乘积2x dA 或2y dA 分别称为该面积元素对y 轴或x 轴的惯性矩或截面二次轴距22y Ax A I x dA I y dA ⎫=⎪⎬=⎪⎭⎰⎰ 分别定义为整个截面对y 轴或x 轴的惯性矩 上述积分遍及整个截面的面积A222x y ρ=+，故有222()p y x AAI dA x y dA I I ρ==+=+⎰⎰任意截面对一点的极惯性矩，等于截面对以该点为原点的任意两正交坐标轴的惯性矩之和面积元素dA 与分别至y 轴和x 轴距离的乘积xydA ，称为该面积元素对两坐标轴的惯性积 定义为整个截面对x 、y 两坐标轴的惯性积，其积分也应遍及整个截面的面积 从上述定义可见，同一截面对于不同坐标轴的惯性矩或惯性积一般是不同的 惯性矩的数值恒为正值，而惯性积可能为正值也可能为负值，也可能等于零 若x 、y 两坐标轴有一为截面的对称轴，则其惯性积恒等于零因在对称轴两侧，处于对称位置的两面积元素dA 的惯性积xydA ，数值相等而正负号相反 致使整个截面的惯性积必等于零，惯性矩和惯性积的单位相同在某些应用中，将惯性矩表示为截面面积A 与某一长度平方的乘积，即2y y I i A =，2x xI i A = 式中，y i 和x i 分别称为截面对y 轴和x 轴的惯性半径，其单位为m 或mm 当已知截面面积A 和惯性矩y I 和x I 时，惯性半径即可从下式求得y i =x i =3．惯性矩和惯性积的平行移轴公式·组合截面的惯性矩和惯性积 3.1 惯性矩和惯性积的平行移轴公式 面积为A 的任意形状的截面截面对任意的x 、y 两坐标轴的惯性矩和惯性积分别为x I 、y I 和xy I 通过截面的形心C 有分别与x 、y 轴平行的C x 、C y 轴称为形心轴 截面对形心轴的惯性矩和惯性积分别为xC I 、yC I 和xCyC I截面上任一面积元素dA 在两坐标系内的坐标(,)x y 与(,)C C x y 间的关系为C x x b =+，C y y a =+式中，a 、b 是截面形心在Oxy 坐标系内的坐标值，即两平行坐标系间的间距 将其代入可得2222()2x C C C AAAAAI y dA y a dA y dA a y dA a dA ==+=++⎰⎰⎰⎰⎰根据惯性矩和静矩的定义，上式右端的各项积分分别为2C xC Ay dA I =⎰，C xC Ay dA S =⎰，AdA A =⎰其中xC S 为截面形心轴C x 的静矩，恒等于零，则原式子可写为2x xC I I a A =+，同理2y yC I I b A =+，xy xCyC I I abA =+a 、b 有正负号，可由截面形心所在的象限来确定，上式称为平行移轴公式应用上式即可根据截面对形心轴的惯性矩或惯性积，计算截面对于形心轴平行的坐标轴的惯性矩惯性矩或惯性积，或进行相反运算3.2 组合截面的惯性矩及惯性积组合截面对某坐标的惯性矩（或惯性积）就等于其各组成部分对同一坐标轴的惯性矩（或惯性积）之和，若截面是由n 个部分组成，则组合截面对x 、y 两轴的惯性矩和惯性积为1n x xi i I I ==∑，1n y yi i I I ==∑，1nxy xyi i I I ==∑式子中，xi I 、yi I 、xyi I 分别为组合截面中组成部分i 对x 、y 两轴的惯性矩和惯性积4．惯性矩和惯性积的转轴公式·截面的主惯性轴和主惯性矩 4.1 惯性矩和惯性积的转轴公式 设一面积为A 的任意形状截面截面对通过其上任意一点O 的两坐标轴x 、y 的惯性矩和惯性积分别为x I 、y I 和xy I 若坐标轴x 、y 绕O 点旋转α角（α角以逆时针转向为正）至1x 、1y 则该截面对新坐标轴1x 、1y 的惯性矩和惯性积分别为1x I 、1y I 和11x y I 截面上任一面积元素dA 在新、老两坐标系内的坐标11(,)x y 与(,)x y 的关系为1cos sin x x y αα=+ 1cos sin y y x αα=-经过展开逐项积分可得，该截面对坐标轴1x 的惯性矩1x I22221cos sin 2sin cos x AAAI y dA x dA xydA αααα=+-⎰⎰⎰根据惯性矩和惯性积的定义，右端的各项积分分别为2x Ay dA I =⎰，2y Ax dA I =⎰，xy AxydA I =⎰将其代入，即得1cos 2sin 222x y x y x xy I I I I I I αα+-=+- 1cos 2sin 222x yx yy xy I I I I I I αα+-=-+11sin 2cos 22x yx y xy I I I I αα-=+以上三式就是惯性矩和惯性积的转轴公式11x y x y I I I I +=+上式表明，截面对于通过同一点的任意一对相互垂直的坐标轴的两惯性矩之和为一常数 并等于截面对该坐标原点的极惯性矩4.2 截面的主惯性主和主惯性矩当坐标轴旋转时，惯性积11x y I 将随着α角作周期性变化，且有正有负 必有一特定的角度0α，使得截面对该坐标轴0x 、0y 的惯性积等于零 截面对其惯性积等于零的一对坐标轴，称为主惯性轴 截面对于主惯性轴的惯性矩，称为主惯性矩当一对主惯性轴的交点与截面的形心重合时，则称为形心主惯性轴 截面对于形心主惯性轴的惯性矩，称为形心主惯性矩设0α角为主惯性轴与原坐标轴之间的夹角 则将0α角代入惯性积的转轴公式并令其等于零，即00sin 2cos 202x yxy I I I αα-+=移项后得02tan 2xy x yI I I α-=-由上式解得的0α的值，即为梁主惯性轴中0x 轴的位置将所得的0α值代入，即得截面的主惯性矩0cos 2I I α-==02sin 2I α-==经化简后即得主惯性矩的计算公式0022x yx x y y I I I I I I +=+=惯性矩1x I 、1y I 都是α角的正弦和余弦函数，α角在0°到360°内变化 因此1x I 、1y I 必有极值由于对通过同一点的任意一对坐标轴的两惯性矩之和为一常数因此其中一个将为极大值，另一个则为极小值，由10x dI d α=和10y dI d α= 解得时惯性矩取得极值的坐标轴的位置的表达式，与上式完全一致可知，截面对通过任一点的主惯性轴的主惯性矩的值也就是通过该点所有轴的惯性矩中的极大值max I 和极小值min I在通过截面形心的一对坐标轴中，若有一个为对称轴，则该对坐标轴就是形心主惯性轴 因为截面对于包括对称轴在内的一对坐标轴的惯性积等于零 在计算组合截面的形心主观性轴是，首先应确定其形心位置 然后通过形心选择一对便于计算惯性矩和惯性积的坐标轴 算出组合截面对这一对坐标轴的惯性矩和惯性积最后利用主惯性矩的计算公式即可确定形心主惯性轴的位置和形心主惯性矩的数值 若组合截面具有对称轴，则包含对称轴的一对相互垂直的形心轴就是形心主惯性轴。

附 录一、应力与强度条件 1、 拉压 []σσ≤=maxN max AF2、 剪切 []ττ≤=AF smax 挤压 []bs bsbsbs A P σσ≤=3、 圆轴扭转 []ττ≤=tmax W T4、 平面弯曲①[]σσ≤=max z max W M②[]t max t z maxmax t y I M σσ≤= max c max max y I Mzc =σ[]c σ≤③[]ττ≤⋅=bI S F z *max z max s max5、斜弯曲 []σσ≤+=maxyyz z max W M W M6、拉（压）弯组合 []σσ≤+=maxmax zW M A N[]t max t z max t σσ≤+=y I M A N z []c max c z z max c σσ≤-=ANy I M 7、圆轴弯扭组合： ①第三强度理论 []στσσ≤+=+=z2222r3W T M 4②第四强度理论 []στσσ≤+=+=z2222r4W T 75.0M 3二、变形及刚度条件 １、 拉压 ∑⎰===∆L Ni N N EAxd )x (F EA L F EA L F L ２、 扭转 ()⎰=∑==p p i i p GI dx x T GI L T GI TL ϕ πθ0180⋅=Φ=p GI T L （m / ） ３、 弯曲(1)积分法:)x (M )x (EIw ''= C x d )x (M )x (EI )x (EIw '+⎰==θD Cx x d ]x d )x (M [)x (EIw ++⎰⎰=(2)叠加法:()21P ,P w …=()()21P f P w ++…， ()21,P P θ=()()++21P P θθ… (3)基本变形表(注意：以下各公式均指绝对值，使用时要根据具体情况赋予正负号)EI ML B =θ EI PL B 22=θ EIqL B 63=θEI2ML w 2B =EI 3PL w 3B = EI 8qL w 4B =PAB MAB A BqL LLEI ML B 3=θ,EI ML A 6=θ EIPL A B 162==θθ EI qL A B 243==θθ EI 16ML w 2c = EI 48PL w 3c = EI384qL w 4c =(4)弹性变形能(注：以下只给出弯曲构件的变形能,并忽略剪力影响,其他变形与此相似,不予写出)EIL M U 22==i i i EI L M 22∑=()⎰EI dxx M 22 (5)卡氏第二定理(注：只给出线性弹性弯曲梁的公式)=∂∂=∆ii P U()()⎰∂∂∑dx P x M EI x M i三、应力状态与强度理论 １、 二向应力状态斜截面应力ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=２、 二向应力状态极值正应力及所在截面方位角22min max )2(2xy y x y x τσσσσσσ+-±+= y x xy σστα--=22tg 0 ３、 二向应力状态的极值剪应力22max )2(xy yx τσστ+-=注：极值正应力所在截面与极值剪应力所在截面夹角为450４、 三向应力状态的主应力：321σσσ≥≥最大剪应力：231max σστ-=5、二向应力状态的广义胡克定律（1）、表达形式之一（用应力表示应变）)(1y x x E μσσε-=)(1x y y E μσσε-= )(y x z E σσμε+-= Gxy xy τγ= （2）、表达形式之二（用应变表示应力）)(12y x x E μεεμσ+-=)(12x y y E μεεμσ+-=0=z σ xy xy G γτ=6、三向应力状态的广义胡克定律()[]z y x x E σσμσε+-=1()z y x ,, Gxy xy τγ= ()zx yz xy ,,LL7、强度理论（1）[]111σσσ≤=r ()3212σσμσσ+-=r []σ≤ []bbn σσ=（2）[]σσσσ≤-=313r ()()()[]213232221421σσσσσσσ-+-+-=r []σ≤ []s s n σσ=8、平面应力状态下的应变分析 （1）αγαεεεεεα2sin 22cos 22⎪⎪⎭⎫ ⎝⎛---++=xyyx yx +-=⎪⎭⎫ ⎝⎛-αεεγα2sin 22y x αγ2cos 2⎪⎪⎭⎫⎝⎛-xy （2）22min max 222⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛-±+=xy y x yx γεεεεεε yx xyεεγα-=02tg四、压杆稳定1、临界压力与临界应力公式（若把直杆分为三类）①细长受压杆 1λλ≥ ()2min2crL EI F μπ= 22crλπσE = ②中长受压杆 21λλλ≥≥ λσb a -=cr③短粗受压杆 2λλ≤ “cr σ”=s σ 或 b σ 2、关于柔度的几个公式 i Lμλ= p21σπλE = b a s 2σλ-=3、惯性半径公式A I i z =（圆截面 4di z =，矩形截面12min bi =（b 为短边长度））五、动载荷（只给出冲击问题的有关公式）能量方程 U V T ∆=∆+∆动荷系数 std 211∆++=hK （自由落体冲击） st20d ∆=g v K （水平冲击） 六、截面几何性质1、 惯性矩（以下只给出公式，不注明截面的形状）⎰=dA I P 2ρ=324d π()44132απ-D D d=α⎰==6442d dA y I z π ()44164απ-D 123bh 123hb323maxd y I W zz π==()43132απ-D 62bh 62hb2、惯性矩平移轴公式A a I I 2zc z +=。

材料力学叠加法附录表是工程设计中经常使用的一种计算方法。

在设计中，我们需要考虑多个因素对物体的影响，例如温度变化、载荷作用等等。

材料力学叠加法就可以帮助我们将这些因素分别计算，然后将其叠加起来得到最终的结果。

以下是材料力学叠加法附录表的详细内容。

一、引言材料力学叠加法是一种常用的结构设计计算方法。

它可以将多种载荷和边界条件的影响分别计算，然后将它们叠加起来得到最终的结果。

这种方法适用于各种不同的结构，例如梁、板、壳等等。

在本文中，我们将主要介绍材料力学叠加法的附录表。

二、材料力学叠加法附录表材料力学叠加法的附录表包括了多个表格，每个表格都对应一个不同的载荷或边界条件。

以下是具体的内容：1. 一般叠加法表格这个表格用于计算多种载荷和边界条件的组合情况。

表格中列出了不同情况下的载荷系数、边界条件系数和相应的计算公式。

使用这个表格时，我们需要将各个系数代入公式中进行计算，然后将它们叠加起来得到最终结果。

2. 温度变化叠加法表格这个表格用于计算温度变化对结构的影响。

表格中列出了不同温度变化情况下的热应力系数和相应的计算公式。

使用这个表格时，我们需要将热应力系数代入公式中进行计算，然后将其叠加到其他载荷的结果中。

3. 偏心叠加法表格这个表格用于计算偏心载荷对结构的影响。

表格中列出了不同偏心距离情况下的偏心系数和相应的计算公式。

使用这个表格时，我们需要将偏心系数代入公式中进行计算，然后将其叠加到其他载荷的结果中。

4. 地震叠加法表格这个表格用于计算地震对结构的影响。

表格中列出了不同地震波形情况下的地震系数和相应的计算公式。

使用这个表格时，我们需要将地震系数代入公式中进行计算，然后将其叠加到其他载荷的结果中。

5. 水压力叠加法表格这个表格用于计算水压力对结构的影响。

表格中列出了不同水压力情况下的水压力系数和相应的计算公式。

使用这个表格时，我们需要将水压力系数代入公式中进行计算，然后将其叠加到其他载荷的结果中。