《材料力学》课程讲解课件附录I平面图形几何性质

第一章 绪论

1.1材料力学的任务

研究构件在外力作用下的受力、变形和破坏的规律，为合理设计构件提供强度、刚度及稳定性分析的基础理论和计算方法。

1.2 变形固体的基本假设

连续性、均匀性、各向同性、小变形

1.3 基本概念

内力、截面法和应力

位移、变形与应变

1.4杆件变形的基本形式

拉伸或压缩

剪切

扭转

弯曲

第二章 杆件的内力.截面法

2.1 轴向拉压. 轴力与轴力图

概念

例题

简单复习轴向拉压、截面法

2.2扭转的概念.扭矩与扭矩图

杆件内力的普遍情况 二维 三维

扭矩

1000602PnMMee

nPMe9549

扭矩图

2.3弯曲的概念.剪力与弯矩

1.对称弯曲

2.梁的计算简图

3.弯曲内力—剪力和弯矩

剪力、弯矩大小和方向

4.例题 指定截面的弯曲内力

2.4剪力方程与弯矩方程.剪力图与弯矩图

剪力方程、弯矩方程

)(xFs )(xM

如何分段、边界条件

实例：悬臂梁均布荷载，简支梁集中力，简支梁集中力偶，简支梁均布荷载

2.5载荷集度、剪力与弯矩之间的关系

内力计算Mechanics of material一段梁上的外力情况剪力图的特征弯矩图的特征最大弯矩所在截面的可能位置q<0向下的均布荷载无荷载集中力FC集中力偶mC上凸的二次抛物线在FS=0的截面一般斜直线或在C处有突变F在C处有尖角或在剪力突变的截面在C处无变化C在紧靠C的某一侧截面向右下倾斜的直线水平直线m在c处有突变

分布荷载集度、剪力和弯矩之间的积分关系

例题：内力图，内力图及载荷图之间的转化

211S2SxxdxxqxFxF21S12FxxdxxxMxM第三章 杆件的应力与强度计算

3.1引言

3.2 拉压杆的应力

ANdAF

平截面假定

斜截面上的应力

cosAFp

2cos，2sin2

3.3材料在拉伸与压缩时的力学性能

材料力学基本概念和公式

第一章 绪论

第一节 材料力学的任务

构成机械和结构的各组成部分统称为构件。保证构件正常或安全工作的基本要求包括强度（即抵抗破坏的能力）、刚度（即抵抗变形的能力）和稳定性（即保持原有平衡状态的能力）。材料力学的任务是研究构件在外力作用下的变形与破坏规律，为合理设计构件提供强度、刚度和稳定性分析的基本理论与计算方法。

第二节 材料力学的基本假设

材料力学的基本假设包括连续性假设（即材料无空隙地充满整个构件）、均匀性假设（即构件内每一处的力学性能都相同）和各向同性假设（即构件某一处材料沿各个方向的力学性能相同，但木材是各向异性材料）。

第三节 内力

内力是指构件内部各部分之间因受力后变形而引起的相互作用力。截面法是用假想的截面把构件分成两部分，以显示并确定内力的方法。截面法求内力的步骤包括用假想截面将杆件切开，一分为二，取一部分得到分离体，对分离体建立平衡方程，求得内力。内力的分类包括轴力F

N

剪力F

S

扭矩T和弯矩M。

第四节 应力

一点的应力是指一点处内力的集中程度。全应力p=lim(ΔF/ΔA)，正应力σ，切应力τ，p=σ^2+τ^2.应力单位包括Pa（1Pa=1N/m^2）、1MPa（1×10^6Pa）和1GPa（1×10^9Pa）。

第五节 变形与应变

变形是指构件尺寸与形状的变化，除特别声明的以外，材料力学所研究的对象均为变形体。弹性变形是指外力解除后能消失的变形，而塑性变形是指外力解除后不能消失的变形或残余变形。材料力学研究的问题限于小变形的情况，其变形和位移远小于构件的最小尺寸，而线应变是无量纲量，在同一点不同方向线应变一般不同。切应变为无量纲量，切应变单位为rad。

第六节 杆件变形的基本形式

等截面直杆是材料力学的研究对象，而杆件变形的基本形式包括拉伸（压缩）、扭转和弯曲。

第二章 拉伸、压缩与剪切

第一节 轴向拉伸（压缩）的特点

轴向拉伸（压缩）的受力特点是外力合力的作用线与杆件轴线重合，而变形特点是沿杆件的轴线伸长和缩短。

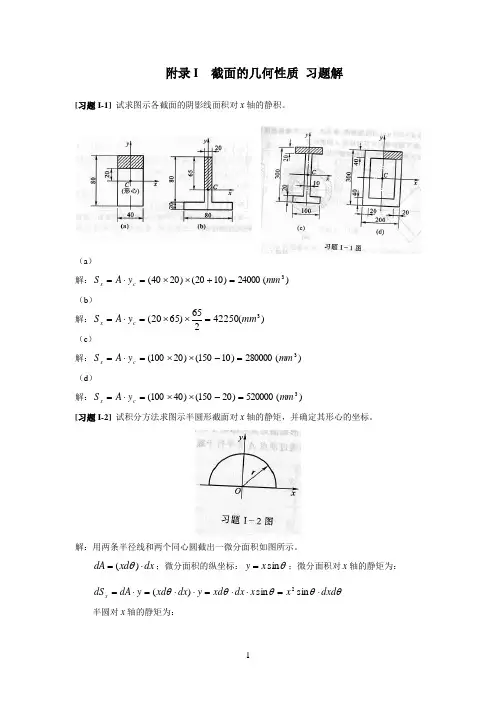
1 附录I 截面的几何性质 习题解

[习题I-1] 试求图示各截面的阴影线面积对x轴的静积。

（a）

解：)(24000)1020()2040(3mmyAScx

（b）

解：)(42250265)6520(3mmyAScx

（c）

解：)(280000)10150()20100(3mmyAScx

（d）

解：)(520000)20150()40100(3mmyAScx

[习题I-2] 试积分方法求图示半圆形截面对x轴的静矩，并确定其形心的坐标。

解：用两条半径线和两个同心圆截出一微分面积如图所示。

dxxddA)(；微分面积的纵坐标：sinxy；微分面积对x轴的静矩为：

dxdxxdxxdydxxdydAdSxsinsin)(2

半圆对x轴的静矩为：

2 32)]0cos(cos[3]cos[]3[sin33003002rrxddxxSrrx

因为cxyAS，所以cyrr232132 34ryc

[习题I-3] 试确定图示各图形的形心位置。

（a）

解：

习题I-3(a): 求门形截面的形心位置

矩形 Li Bi Ai Yci AiYci Yc 离顶边

上 400 20 8000 160 1280000

左 150 20 3000 75 225000

右 150 20 3000 75 225000

14000 1730000 123.6 46.4

Ai=Li*Bi Yc=∑AiYci/∑Ai

(b)

解：

习题I-3(b): 求L形截面的形心位置

矩形 Li Bi Ai Yci AiYci Yc Xci

AiXci Xc

下 160 10 1600 5 8000 80 128000

左 90 10 900 55 49500 5 4500

材料力学电子教材

淮阴工学院建筑工程系

2006.12 主要符号表

符 号

A

D、d

E

F

Fcr

Fd

FN

FQ

G

Iy、Iz

IP

Iyz

iy、iz kd M、My、Mz Mx

Me

Ms

Mu

N

n

nr

nst

p

P

q

R、r

r

Sy、Sz

T t

Vc

Vε

vd

vv

vε

W 含 义

面积 直径

弹性模量

集中力 临界力 动荷载 轴力

剪力 切变模量 惯性矩 极惯性矩 惯性积

惯性半径

动荷因素

弯矩

扭矩 外力偶矩

屈服弯矩 极限弯矩 循环次数 安全因素，转速 疲劳安全因素 稳定安全因素 总应力，压强 功率

均布荷载集度 半径

循环特征 面积矩，静矩 扭转外力偶矩 时间

余应变能 应变能 形状改变能密度 体积改变能密度 应变能密度 重力，外力功，弯曲 截面系数 符 号

Wc

WP

w

θ

φ

γ

Δ

Δl

ε

εu

λ

µ ν

σ

σb

σbs

σcr

σd

σe

σp

σr

σs

σu

σ-1

[σ]

τ

[τ] 含 义

余功 扭转截面系数 挠度

梁横截面转角，单位长度

相对扭转角，体积应变

相对扭转角，折减因数

切应变

位移 伸长（缩短）变形 线应变

极限应变

柔度 长度系数 泊松比 正应力

强度极限

挤压应力

临界应力

动应力 弹性极限 比例极限

相当应力，疲劳极限

屈服极限

极限应力 对称循环疲劳极限 容许正应力

切应力 容许切应力

第一章 绪论·基本概念

§1-1 材料力学的任务

§1-2 变形固体的概念及其基本假设

§1-3 杆件及其变形形式

§1-4 应力

§1-5 位移和应变

§1-6 材料力学的特点思考题

思考题

习 题

第二章 轴向拉伸和压缩

§2-1 概 述

§2-2 拉压杆件横截面上的正应力

§2-3 应力集中的概念

§2-4 拉压杆件的变形

§2-5 拉伸和压缩时材料的力学性质

§2-6 几种新材料的力学性质简介

§2-7 拉压杆件的强度计算

材料力学

1.材料力学研究内容

⑴研究物体在外力作用下的应力、变形和能量，统称为应力分析；研究对象仅限于杆、轴、梁等物体，其几何特征是纵向尺寸远大于横向尺寸，这类物体统称为杆或杆件。

⑵研究材料在外力和温度作用下所表现出的力学性能和失效行为；研究对象仅限于材料的宏观力学行为，不涉及材料的微观机理。

研究目的设计出杆件或零部件的合理形状和尺寸，以保证它们具有足够的强度、刚度和稳定性。

2.杆件的受力与变形形式

⑴拉伸或压缩

⑵剪切

⑶扭转

⑷弯曲

⑸组合受力和变形

拉杆、压杆或柱、轴、梁受力特点

3.材料的基本假定

⑴各向同性假定

⑵均匀连续性假定

⑶平截面假定

4.受力分析方法

⑴截面法：应用假想截面将弹性体截开，分成两部分，考虑其中任意一部分平衡，从而确定截面上的内力的方法。

弹性体受力、变形的第二特征是变形协调。P9［例题1-1］

平衡方程+变形协调方程

0xF

0yF

0cM

P31［例题2-6］

5.应力应变相互关系

E、G

6.轴力与轴力图

正负号规定：拉正，压负。

⑴确定约束力。

⑵根据杆件上作用的荷载及约束力确定控制面，也就是轴力图的分段点。

⑶应用截面法，对截开的部分杆件建立平衡方程，确定控制面上的轴力数值。

⑷建立NxF坐标系，将所求得的轴力值标在坐标系中，画出轴力图。

P21［例题2-1］

7.变形计算

变形NFllEA

应变NFllEAE

横向变形yx 泊松比

P25［例题2-2］

8.拉伸与压缩杆件的强度设计

⑴强度校核

max

⑵尺寸设计

maxNNFFAA

⑶确定杆件或结构所能承受的许用荷载

maxNNPFFAFA

P28［例题2-4/5］

9.拉伸与压缩杆件斜截面上的应力

2cos=cosNPxFFAA

《材料力学》课程教学大纲

适用于本科机械设计制造及其自动化专业

学分3.5 总学时：56 理论学时：48 实验/实践学时： 8

一、课程的性质、任务和要求

《材料力学》是工科专业基础课，必修。本课程共56学时，3.5学分。

《材料力学》课程的主要任务是：通过该课程的学习，要求学生掌握等直杆件的强度、刚度及轴向受压杆件的稳定性的计算等；能运用强度、刚度及稳定性条件对杆件进行校核、截面设计及载荷确定等简单计算工作；初步了解材料的机械性能及材料力学实验的基本知识和操作技能；初步学会应用材料力学的理论和方法解决一些简单的工程实际问题；为学习有关的后继课程打好必要的基础。

学习本课程后，应达到下列基本要求：

1．对材料力学的基本概念和基本分析方法有明确的认识；

2．能熟练地画出杆件在基本变形下的内力图，进行应力和位移、强度和刚度的计算；

3．掌握应力状态理论和组合变形下杆件的强度计算；

4．了解压杆的稳定性概念，会计算轴向受压杆的临界力和临界应力；

5．了解低碳钢和灰口铸铁的基本力学性能及其测定方法；

6．掌握简单超静定问题的求解方法；

7．掌握电测实验应力分析的基本原理和方法。

二、本课程与其它课程的关系、主要参考教材

本课程的先修课程为：高等数学、工程图学、理论力学。

选用教材：《材料力学Ⅰ》（第5版），刘鸿文主编，高等教育出版社，2010

参考书目：

[1]《材料力学Ⅰ》（第5版），孙训方主编，高等教育出版社，2009

[2]《材料力学Ⅰ》（第3版），单辉祖，高等教育出版社，2009

[3]《材料力学》，Timoshenko（铁木辛柯）编，科学出版社，1978

三、课程内容

1．绪论

主要内容：材料力学的任务及研究对象；变形固体的基本假设；力与内力、截面法与应力、线变形和角变形的概念；杆件变形的基本形式。

2．拉伸、压缩与剪切

主要内容：轴向拉伸与压缩的概念与实例；直杆横截面上的内力、应力及斜截面上的应力计算；安全系数与许用应力的应用、拉压杆件的强度计算；轴向拉伸与压缩时杆件的纵向变形、线应变、横向变形计算；泊松比、虎克定律、弹性模量，抗拉(压)刚度、应力集中的概念；金属材料拉伸和压缩时的力学性能；简单拉(压)超静定问题、热应力和装配应力的解法；剪切和挤压的实用计算。

附录I 截面图形的几何性质

- 1 -

附录Ⅰ 截面图形的几何性质

I-1

填空题：

I-1(1)

当一个正方形的边长和一个圆形的直径相等时，两图形对

其形心轴的惯性矩之比应为

π316

。

I-1(2)

若已知图示平面图形对 A轴的惯性矩为3

427

bh

，则图

形对C轴的惯性矩为 3

43bh

，对D轴的惯性矩为 3

49bh

。

I-1(3)

题图所示的截面由两个直径为d

的圆构成，该截面关于

图示坐标系中的

=

xI

32π4d

，=

yI

325π4d

，=

xyI

0

。

I-1(4)

题图所示的矩形位于坐标平面的第四象限，该图形的

=

xS

22

bh−

，=

yS

22

hb

，=

xyI

422

hb−

。

I-1(5)

题图所示的两个半圆的组合截面中，A-A轴平行于

底边，只有当

=a

⎟⎟

⎠⎞

⎜⎜

⎝⎛

+++

dDdDdD22

π32

时，才能使截

面对A-A轴的惯性矩为最小。

I-1(6)

如图，边长为a

的正方形关于平行于对角线的轴线AB的

惯性矩等于

1274a

。

题 I-1(3) 图

x y

A B

题 I-1(6) 图

d

D AA

a

题 I-1(5) 图

A

h

b h

h

B

C

D

题 I-1(2) 图

b y

x

O

h

题 I-1(4) 图 工程力学习题解答

- 2 -

I-2

单选题：

I-2(1)

边长为4a的正方形，在如图位置挖去一个边长为a

的小正方形，余下的阴影图形对坐标轴x、y、x′、y′的静

矩分别为

yxyxSSSS

′′,,,

，其中只有 C 是对的。

A．

23

a

S

x=

B

．3

22

aS

y=

C．0=

′xS

D．0=

′yS

I-2(2)

某个T字形截面在形心轴x轴以上和以下的面积对该

轴的静矩分别为

xS′

和

xS′′

，两者之间的关系应为 B 。

A．

xxSS′′=′

B．

xxSS′′−=′

C．

xxSS′′>′

D

．

xxSS′′<′

I-2(3)

槽钢组合后的两种截面对形

心轴x、y和x′、y′的惯性矩之间的关

材料力学课程教学大纲

一、 课程的性质和任务 材料力学是一门技术基础课。通过材料力学的学习，要求学生对杆件的

强度、刚度和稳定性问题具有明确的基本概念、必要的基础理论知识、比较熟练

的计算能力、一定的分析能力和实验能力。本课程在高级工程技术人才的培养过

程中，具有建立专业技术基础，培养开发创新能力的作用。 二、 课程的基本内容 第一章、绪论 材料力学的任务，本课程的特点与应用、发展变形固体的基本假设，外力及

其分类，内力、截面法和应力的概念，变形与应变，杆件变形的基本形式。

重点掌握截面法、内力、应力、位移、变形和应变的概念，建立材料力学分

析问题的思想。 第二章、拉伸、压缩与剪切 轴向拉伸与压缩的概念与实例，轴向拉伸或压缩时横截面上内力和应力，直

杆轴向拉伸或压缩时斜截面上的应力，材料在拉伸时的力学性能，材料在压缩时

的力学性能，温度和时间对材料力学性能的影响，失效、安全系数和强度计算，

轴向拉伸或压缩时的变形，轴向拉伸或压缩时的变形能，拉伸、压缩静不定问题，

温度应力和装配应力，应力集中的概念，剪切和挤压的实用计算。 掌握拉（压）杆的内力、应力、位移、变形和应变概念。掌握单向拉压的胡

克定律，掌握材料的拉、压力学性能，了解测试方法。掌握强度条件的概念，会

进行拉压强度和刚度计算。建立应力集中的概念。掌握剪切、挤压的概念和实用

计算。 第三章、扭转 扭转的概念和实例，外力偶矩的计算，扭矩和扭矩图，纯剪切，圆轴扭转时

的应力，圆轴扭转时的变形，圆柱形密圈螺旋弹簧的应力和变形，非圆截面杆扭

转的概念，薄壁杆件的自由扭转。 掌握纯剪概念，剪切胡克定律，切应力互等定理。掌握轴的内力，圆轴扭转

应力和变形，建立强度和刚度条件，会进行扭转强度和刚度的计算。了解非圆截

面杆扭转。 第四章、弯曲内力 弯曲的概念和实例，受弯杆件的简化，剪力和弯矩，剪力方程和弯矩方

程，剪力图和弯矩图，载荷集度、剪力和弯矩间的关系，平面曲杆的弯曲内力。

掌握平面弯曲内力，能够计算较复杂受载下的内力，列内力方程，利用载荷集度、

附录 截面图形的几何性质

一、是非判断题

⒈ 图形对某一轴的静矩为零，则该轴必定通过图形的形心。（ √

）

⒉ 图形在任一点只有一对主惯性轴。（ ×

）

⒊ 有一定面积的图形对任一轴的轴惯性矩必不为零。（ √

）

⒋ 图形对过某一点的主轴的惯性矩为图形对过该点所有轴的惯性矩中的极值。（ √

）

二、填空题

⒈ 组合图形对某一轴的静矩等于 各组成图形对同一轴静矩 的代数和。

⒉ 图形对任意一对正交轴的惯性矩之和，恒等于图形对 两轴交点的极惯性矩 。

⒊ 如果一对正交轴中有一根是图形的对称轴，则这一对轴为图形 主惯性轴 。

⒋ 过图形的形心且 图形对其惯性积等于零 的一对轴为图形的形心主惯性轴。

三、选择题

⒈ 图形对于其对称轴的（ A ）

A 静矩为零，惯性矩不为零； B 静矩和惯性矩均为零

C 静矩不为零，惯性矩为零； D 静矩和惯性矩均不为零

⒉ 直径为d

的圆形对其形心主轴的惯性半径=（ C ）。i

A d/2 B d/3 C d/4 D d/8

⒊ 图示截面图形中阴影部分对形心主轴的惯性矩=（ C ）。z

ZI

A

B

123234

dDD



63234

dDD



C

D

126434

dDD



66434

dDD



D

dD

z四、计算题

1、求图示平面图形中阴影部分对z轴的静矩。

2

32.0)2.06.0(4.0bhhhhbS

Z

8842422222

bhhHBhh

bhHhhH

BS

Z















2、求图示平面图形对z

、y轴的惯性矩。

4523

23

1023.251040

121040

251040

123010

mmIII

IIIZ







由于图形对称，45

1023.2mmII

ZY3、试求图示平面图形的形心主惯性轴的位置，并求形心主惯性矩。

mmy

C7.56

10020201401010020902010





472323

1021.17.46200.10

12201003.3320140

《材料力学习题》 班级： 学号： 姓名：

1 第一章 绪论

1-1矩形平板变形后为平行四边形，水平轴线在四边形AC边保持不变。求(1)沿AB边的平均线应变； (2)平板A点的剪应变。

（答案：εAB=7.93×10-3 γXY=-1.21×10-2rad）

第二章 拉伸、压缩与剪切

2-1 试画图示各杆的轴力图，并指出轴力的最大值。

2-2 一空心圆截面杆，内径d=30mm，外径D=40mm，承受轴向拉力F=KN作用，试求横截面上的正应力。（答案：MPa7.72） 《材料力学习题》 班级： 学号： 姓名：

2 2-3 题2－1 c 所示杆，若该杆的横截面面积A=502mm，试计算杆内的最大拉应力与最大压应力

（答案：MPat60max, MPac40max,）

2.4图示轴向受拉等截面杆，横截面面积A=5002mm，载荷F=50KN。试求图示截面m-m上的正应力与切应力，以及杆内的最大正应力与最大切应力。

（答案：MPaMPaMPaMPa50 ; 100 ; 24.49 ; 32.41maxmax） 《材料力学习题》 班级： 学号： 姓名：

3

2.5如图所示，杆件受轴向载荷F作用。该杆由两根木杆粘接而成，若欲使粘接面上的正应力为其切应力的二倍，则粘接面的方位角应为何值（答案： 6.26）

2.6 等直杆受力如图所示，试求各杆段中截面上的轴力，并绘出轴力图。

《材料力学习题》 班级： 学号： 姓名：

4

2.7某材料的应力－应变曲线如图所示，图中还同时画出了低应变去区的详图，试确定材料的弹性模量E、屈服极限s、强度极限b、与伸长率，并判断该材料属于何种类型（塑性或脆性材料）。

《材料力学》课程教学大纲

学分：4.5 总学时：72 理论学时：62 实验/实践学时：10

一、课程性质与任务

《材料力学》是车辆工程的专业基础课。本课程共72学时，4.5学分，考试课。

《材料力学》是由基础理论课过度到设计课程的技术基础课。它是变形固体力学的基础，又是有关专业后续课程的需要。通过本课程的学习，使学生建立起正确的变形固体力学基本概念，掌握分析工程中强度、刚度、稳定性问题的基本方法，提高工程计算能力和实验分析能力等方面均有重要作用，它与其它课程共同完成培养高级工程技术人员的任务。

二、课程的基本要求

学习本课程后，应达到下列基本要求：

1．掌握构件强度、刚度、稳定性的基本概念，掌握杆件四种基本变形及组合变形的定义，能熟练判定杆件的变形种类。

2．掌握用截面法求杆件内力的基本方法，能熟练地求解任一指定截面的内力，并能绘制杆件的内力图。

3．熟悉等截面杆件横截面上应力的分析方法（基本变形）：实验-假设-变形几何关系、物理、静力平衡；能熟练求解四种基本变形有关的应力计算、分布及危险点判定和强度计算。

4．掌握组合变形构件强度分析方法-叠加法，了解其原理和使用条件，熟练掌握组合变形构件的强度计算问题。

5．掌握各基本定理、定律及假设（剪应力互等定理、剪切虎克定律、广义虎克定律、强度理论等），并能熟练应用。

6．掌握并能熟练求解基本变形构件的变形、位移问题，并能进行相关的刚度计算。

7．掌握一点应力状态的表示方法，能熟练地从受力构件中取原始单元体，并能用解析法、图解法求解相关问题。

8．掌握静不定问题的基本概念，掌握用变性比较法求解一次静不定问题。

9．掌握压杆稳定的基本概念，并能熟练地进行稳定计算。

10．熟悉动载荷问题的分析方法，并能熟练求解相关问题；掌握交变应力的基本概念，会进行疲劳强度计算。

11．掌握与平面图形有关的几何量（静矩、形心、惯性矩等）的基本概念及计算，了解形心轴、主惯性轴等概念。

1 第一章 绪论 第一节 材料力学的任务 1、组成机械与结构的各组成部分，统称为构件。 2、保证构件正常或安全工作的基本要求：a)强度，即抵抗破坏的能力；b)刚度，即抵抗变形的能力；c)稳定性，即保持原有平衡状态的能力。 3、材料力学的任务：研究构件在外力作用下的变形与破坏的规律，为合理设计构件提供强度、刚度和稳定性分析的基本理论与计算方法。 第二节 材料力学的基本假设 1、连续性假设：材料无空隙地充满整个构件。 2、均匀性假设：构件内每一处的力学性能都相同 3、各向同性假设：构件某一处材料沿各个方向的力学性能相同。木材是各向异性材料。 第三节 内力 1、内力：构件内部各部分之间因受力后变形而引起的相互作用力。 2、截面法：用假想的截面把构件分成两部分，以显示并确定内力的方法。 3、截面法求内力的步骤：①用假想截面将杆件切开，一分为二；②取一部分，得到分离体；③对分离体建立平衡方程，求得内力。 4、内力的分类：轴力NF；剪力SF；扭矩T；弯矩M 第四节 应力 1、一点的应力： 一点处内力的集（中程）度。 全应力0limAFpA；正应力σ；切应力τ；22p 2、应力单位：Pa （1Pa=1N/m2，1MPa=1×106 Pa，1GPa=1×109 Pa） 第五节 变形与应变 1、变形：构件尺寸与形状的变化称为变形。除特别声明的以外，材料力学所研究的对象均为变形体。 2、弹性变形：外力解除后能消失的变形成为弹性变形。 3、塑性变形：外力解除后不能消失的变形，称为塑性变形或残余变形。 4、小变形条件：材料力学研究的问题限于小变形的情况，其变形和位移远小于构件的最小尺寸。对构件进行受力分析时可忽略其变形。 5、线应变：ll。线应变是无量纲量，在同一点不同方向线应变一般不同。 2 6、切应变：tan。切应变为无量纲量，切应变单位为rad。 第六节 杆件变形的基本形式 1、材料力学的研究对象：等截面直杆。 2、杆件变形的基本形式：拉伸（压缩）、扭转、弯曲 第二章 拉伸、压缩与剪切 第一节 轴向拉伸（压缩）的特点 1、受力特点：外力合力的作用线与杆件轴线重合。 2、变形特点：沿杆件的轴线伸长和缩短。 第二节 拉压杆的内力和应力 1、内力：拉压时杆横截面上的为轴力 。 2、轴力正负号规定：拉为正、压为负。 3、轴力图三个要求：上下对齐，标出大小，标出正负。 4、横截面上应力：应力在横截面上均匀分布 第三节 材料拉伸和压缩时的力学性能 1、低碳钢拉伸时的应力–应变曲线：（见图） 2、低碳钢拉伸时经过的四个阶段：弹性阶段，屈服阶段，强化阶段，局部变形阶段。 3、胡克定律：应力小于比例极限p时，应力与应变成正比，材料服从胡克定律：E，E为（杨氏）弹性模量，是材料常数，单位与应力相同。钢的弹性模量E=210GPa。 4、低碳钢拉伸时四个强度指标：弹性极限e；比例极限p；屈服极限s；强度极限b。

1 任务七 平面图形的几何性质

一、填空题

1. 图示BH的矩形中挖掉一个bh的矩形，则此平面图形的zW=( 2366zBHbhWH )。

2. 对图示矩形，若已知xI、yI、b、h，则

11xyII( 1122()/12yzyzIIIIbhbh )。

3. 任意平面图形至少有( 1 )对形心主惯性轴，等边三角形有( 无穷多 )对形心主惯性轴。

4.在边长为2a的正方形的中心部挖去一个边长为a的

正方形，则该图形对y轴的惯性矩为( 454a )。

5.图形对所有平行轴的惯性矩中，图形对形心轴的惯性矩为( 最小 )。

6.对直径为d的圆形截面，它的惯性半径为( i=d/4 )。

二、选择题

1.在下列关于平面图形的结论中，（ D ）是错误的。

A.图形的对称轴必定通过形心； B.图形两个对称轴的交点必为形心；

C.图形对对称轴的静矩为零； D.使静矩为零的轴为对称轴。

2.在平面图形的几何性质中，（ D ）的值可正、可负、也可为零。

A.静矩和惯性矩 B.极惯性矩和惯性矩 C.惯性矩和惯性积 D.静矩和惯性积。

3.设矩形对其一对称轴z的惯性矩为I，则当其长宽比保持不变。而面积增加1倍时，该矩形对z的惯性矩将变为（ D ）。

A. 2I B. 4I C. 8I D. 16I

4.若截面图形有对称轴，则该图形对其对称轴的（ A ）。

A.静矩为零，惯性矩不为零 B.静矩不为零，惯性矩为零

C.静矩和惯性矩均为零 D.静矩和惯性矩均不为零

5．若截面有一个对称轴，则下列说法中（ D ）是错误的。

A. 截面对对称轴的静矩为零；

B. 对称轴两侧的两部分截面，对对称轴的惯性矩相等；

C. 截面对包含对称轴的正交坐标系的惯性积一定为零；

第七章

平面图形的几何性质

研究截面几何性质的意义

从上章介绍的应力和变形的计算公式中可以看出，应力

和变形不仅与杆的内力有关，而且与杆件截面的横截面面积

A、极惯性矩IP、抗扭截面系数WP等一些几何量密切相关。

因此要研究构件的的承载能力或应力，就必须掌握截面几何

性质的计算方法。

另一方面，掌握截面的几何性质的变化规律，就能灵活

机动地为各种构件选取合理的截面形状和尺寸，使构件各部

分的材料能够比较充分地发挥作用，尽可能地做到“物尽其

用”，合理地解决好构件的安全与经济这一对矛盾。

截面的几何性质 第一节 静矩

一、静距的概念

AySzddAzSydd





AAyyAAzz

AzSSAySS

dddd

z y dA

y z 静距是面积与它到轴的距离之积。

平面图形的静矩是对一定的坐标而言的，同一平面图形对不同的坐标轴，其静矩显然不同。静矩的数值可能为正，可能为负，也可能等于零。它常用单位是m3或mm3。

截面的几何性质

形心

d

A

z y

y z Cx

Cy



AyAyAzAz

CC







AydAyAzdAz

ACAC





ASyASz

zCyC



CyCzzASyAS

平面图形对z轴（或y轴

）的静矩，等于该图形面积

A与其形心坐标yC（或zC）

的乘积。

截面的几何性质

当坐标轴通过平面图形的形心时，其静矩为零；反

之，若平面图形对某轴的静矩为零，则该轴必通过平面

图形的形心。

如果平面图形具有对称轴，对称轴必然是平面图形

的形心轴，故平面图形对其对称轴的静矩必等于零。



CyCzzASyA

S截面的几何性质

二、组合图形的静矩

根据平面图形静矩的定义，组合图形对z轴（或y轴）的静

矩等于各简单图形对同一轴静矩的代数和，即







n

iCiiCnnCCyn

iCiiCnnCCz

zAzAzAzASyAyAyAyAS

805 材料力学 考试大纲

1、绪论：变形固体的基本假设、内力、截面法、应力、应变、虎克定律。

2、轴向拉伸和压缩：概念和实例、横截面上的内力和应力、材料在拉伸时 的力学性能、许用应力、强度条件、拉伸和压缩时的变形、拉伸和压缩时 的静不定问题。

3、剪切，剪切和挤压的强度计算。

4、扭转，外力偶矩与扭矩的计算、薄壁圆筒的扭转、纯剪切、圆轴扭转时 的应力和变形、强度和刚度计算。

5、平面图形的几何性质：静矩和形心、惯性矩、惯性积、惯性半径、平行 移轴公式、转轴公式、主惯性轴、主惯性矩。

6、弯曲内力：剪力与弯矩、剪力与弯矩方程、剪力图与弯矩图、载荷集度、 剪力和弯矩间的微分关系、叠加法作弯矩图、平面曲杆的弯曲内力。

7、抗弯强度：弯曲正应力、弯曲切应力、抗弯强度计算、提高抗弯强度的措 施、弯曲中心。

8、弯曲变形：挠度和转角、梁的刚度条件、挠曲线的近似微分方程式、积分 法求梁的变形、叠加法求梁的变形。

9、应力状态理论：一点应力状态的概念、平面应力分析的解析法与图解法、

三向应力状态简介、平面应变状态分析、广义虎克定律、变形比能。

10、组合变形和强度理论：组合变形的概念、斜弯曲、拉伸或压缩与弯曲的 组合、偏心压缩与截面核心、强度理论的概念、四种常用的强度理论 扭转和弯曲的组合。

11、交变应力：交变应力与疲劳失效、交变应力的循环特征、应力幅和平均应力、持久极限、影响构件持久极限的因素、对称循环下构件的疲劳强度计算、持久极限曲线。

12、压杆稳定：压杆稳定的概念、两端铰支细长压杆的临界力、不同杆端约束细长压杆的临界力、欧拉公式的适用范围、经验公式、压杆稳定性计算。

参考书：《材料力学》（Ⅰ、Ⅱ册）刘鸿文 高等教育出版社（第四版）

第 1 页 共 17 页

初中数学课件几何画板（精选12篇）

初中数学课件几何画板 1

教学目标：

1、使学生理解切割线定理及其推论；

2、使学生初步学会运用切割线定理及其推论、

3、通过对切割线定理及推论的证明，培养学生从几何图形归纳出几何性质的能力；

4、通过对切割线定理及其推论的初步运用，培养学生的分析问题能力、在上节我们曾经学到相交弦定理及其推论，它反映了圆中两弦的数量关系；我们可以用同样的方法来研究圆的一条切线和一条割线的数量关系、

教学重点：

使学生理解切割线定理及其推论，它是以后学习中经常用到的重要定理、

教学难点：

学生不能准确叙述切割线定理及其推论，针对具体图形学生很容易得到数量关系，但把它用语言表达，学生感到困难、教学过程：

一、新课引入：

我们已经学过相交弦定理及其推论，现在我们用同样的数学思想方法来研究圆的另外的比例线段、

二、新课讲解：

现在请同学们在练习本上画O，在O外一点P引O的切线PT，切点为T，割线PBA，以点P、B、A、T为顶点作三角形，可以作几个三角形呢？它们中是否存在着相似三角形？如果存在，你得到了怎样的比例线段？可转化成怎样的积式？现在请同学们打开练习本，按要求作O的切线PT和割线PBA，后研究讨论一下、

学生动手画图，完成证明，教师巡视，当所有学生都得到数量关系式时，教师打开计算机或幻灯机用动画演示、

最终教师指导学生把数量关系转成语言叙述，完成切割线定理及其推论、

1、切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆

第 2 页 共 17 页

交点的两条线段长的比例中项、

2关系式：PT=PA·PB

2、切割线定理推论：从圆外一点引圆的两条割线、这一点到每条割线与圆的交点的两条线段长的积相等、