八上 线段、角的轴对称性 知识点+例题+练习 (非常好 分类全面)

2.4 线段、角的轴对称性一、选择题1．如图，四边形ABCD中，AC垂直平分BD，垂足为E，下列结论不一定成立的是（）A．AB=AD B．AC平分∠BCD C．AB=BD D．△BEC≌△DEC2．如图，△ABC中，BC＞AB＞AC．甲、乙两人想在BC上取一点P，使得∠APC=2∠ABC，其作法如下：（甲）作AB的中垂线，交BC于P点，则P即为所求（乙）以B为圆心，AB长为半径画弧，交BC于P点，则P即为所求对于两人的作法，下列判断何者正确？（）A．两人皆正确B．两人皆错误C．甲正确，乙错误D．甲错误，乙正确3．如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A=60°，∠ABD=24°，则∠ACF的度数为（）A．48° B．36° C．30° D．24°4．如图，在△ABC中，AB=AC，∠BAC=100°，AB的垂直平分线DE分别交AB、BC于点D、E，则∠BAE=（）A．80° B．60° C．50° D．40°5．如图，△ABC中，AB=5，AC=6，BC=4，边AB的垂直平分线交AC于点D，则△BDC的周长是（）A．8 B．9 C．10 D．116．如图，在Rt△ABC中，∠C=90°，AB的垂直平分线交AC于点D，交AB于点E．若BC=2，AC=4，则BD=（）A．B．2 C．D．37．如图，地面上有三个洞口A、B、C，老鼠可以从任意一个洞口跑出，猫为能同时最省力地顾及到三个洞口（到A、B、C三个点的距离相等），尽快抓到老鼠，应该蹲守在（）A．△ABC三边垂直平分线的交点B．△ABC三条角平分线的交点C．△ABC三条高所在直线的交点D．△ABC三条中线的交点8．如图，在△ABC中AB的垂直平分线交AB于点D，交线段BC于点E．BC=6，AC=5，则△ACE的周长是（）A．14 B．13 C．12 D．119．如图，在△ABC中，∠A=36°，AB=AC，AB的垂直平分线OD交AB于点O，交AC于点D，连接BD，下列结论错误的是（）A．∠C=2∠A B．BD平分∠ABCC ．S △BCD =S △BOD D ．点D 为线段AC 的黄金分割点10．如图，在△ABC 中，AB=AC ，∠A=120°，BC=6cm ，AB 的垂直平分线交BC 于点M ，交AB 于点E ，AC 的垂直平分线交BC 于点N ，交AC 于点F ，则MN 的长为（ ）A ．4cmB ．3cmC ．2cmD ．1cm11．如图，在△ABC 中，AB=AC ，∠A=40°，AB 的垂直平分线交AB 于点D ，交AC 于点E ，连接BE ，则∠CBE 的度数为（ ）A ．70°B ．80°C ．40°D ．30°12．如图，在△ABC 中，AC=4cm ，线段AB 的垂直平分线交AC 于点N ，△BCN 的周长是7cm ，则BC 的长为（ ）A ．1cmB ．2cmC ．3cmD ．4cm13．如图，在Rt△ABC中，∠ACB=60°，DE是斜边AC的中垂线，分别交AB、AC于D、E两点．若BD=2，则AC的长是（）A．4 B．4 C．8 D．814．如图，锐角三角形ABC中，直线L为BC的中垂线，直线M为∠ABC的角平分线，L与M相交于P点．若∠A=60°，∠ACP=24°，则∠ABP的度数为何？（）A．24° B．30° C．32° D．36°二、填空题15．点P在线段AB的垂直平分线上，PA=7，则PB=______．16．等腰△ABC的底角为72°，腰AB的垂直平分线交另一腰AC于点E，垂足为D，连接BE，则∠EBC的度数为______．17．如图，在等腰三角形ABC中，AB=AC，DE垂直平分AB，已知∠ADE=40°，则∠DBC=______°．18．如图，在△ABC中，∠C=31°，∠ABC的平分线BD交AC于点D，如果DE垂直平分BC，那么∠A=______°．19．如图，△ABC中，DE是BC的垂直平分线，DE交AC于点E，连接BE．若BE=9，BC=12，则cosC=______．20．已知点P在线段AB的垂直平分线上，PA=6，则PB=______．21．如图，△ABC中，AB+AC=6cm，BC的垂直平分线l与AC相交于点D，则△ABD的周长为______cm．22．如图，△ABC中，∠A=40°，AB的垂直平分线MN交AC于点D，∠DBC=30°，若AB=m，BC=n，则△DBC的周长为______．23．如图，在▱ABCD中，AB=3，BC=5，对角线AC、BD相交于点O，过点O作OE⊥AC，交AD于点E，连接CE，则△CDE的周长为______．2.4 线段、角的轴对称性参考答案与试题解析一、选择题1．如图，四边形ABCD中，AC垂直平分BD，垂足为E，下列结论不一定成立的是（）A．AB=AD B．AC平分∠BCD C．AB=BD D．△BEC≌△DEC【考点】线段垂直平分线的性质．【分析】根据线段垂直平分线上任意一点，到线段两端点的距离相等可得AB=AD，BC=CD，再根据等腰三角形三线合一的性质可得AC平分∠BCD，EB=DE，进而可证明△BEC≌△DEC．【解答】解：∵AC垂直平分BD，∴AB=AD，BC=CD，∴AC平分∠BCD，EB=DE，∴∠BCE=∠DCE，在Rt△BCE和Rt△DCE中，，∴Rt△BCE≌Rt△DCE（HL），故选：C．【点评】此题主要考查了线段垂直平分线的性质，以及等腰三角形的性质，关键是掌握线段垂直平分线上任意一点，到线段两端点的距离相等．2．如图，△ABC中，BC＞AB＞AC．甲、乙两人想在BC上取一点P，使得∠APC=2∠ABC，其作法如下：（甲）作AB的中垂线，交BC于P点，则P即为所求（乙）以B为圆心，AB长为半径画弧，交BC于P点，则P即为所求对于两人的作法，下列判断何者正确？（）A．两人皆正确B．两人皆错误C．甲正确，乙错误D．甲错误，乙正确【考点】线段垂直平分线的性质；圆的认识；作图—基本作图．【分析】根据甲乙两人作图的作法即可证出结论．【解答】解：甲：如图1，∵MN是AB的垂直平分线，∴AP=BP，∴∠B=∠BAP，∵∠APC=∠B+∠BAP，∴∠APC=2∠ABC，∴甲正确；乙：如图2，∵AB=BP，∴∠BAP=∠APB，∵∠APC=∠BAP+∠B，∴∠APC≠2∠ABC，∴乙错误；故选C．【点评】本题考查了线段的垂直平分线的性质，三角形外角的性质，正确的理解题意是解题的关键．3．如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A=60°，∠ABD=24°，则∠ACF的度数为（）A．48° B．36° C．30° D．24°【考点】线段垂直平分线的性质．【分析】根据角平分线的性质可得∠DBC=∠ABD=24°，然后再计算出∠ACB的度数，再根据线段垂直平分线的性质可得BF=CF，进而可得∠FCB=24°，然后可算出∠ACF的度数．【解答】解：∵BD平分∠ABC，∴∠DBC=∠ABD=24°，∵∠A=60°，∴∠ACB=180°﹣60°﹣24°×2=72°，∵BC的中垂线交BC于点E，∴BF=CF，∴∠FCB=24°，∴∠ACF=72°﹣24°=48°，故选：A．【点评】此题主要考查了线段垂直平分线的性质，以及三角形内角和定理，关键是掌握线段垂直平分线上任意一点，到线段两端点的距离相等．4．如图，在△ABC中，AB=AC，∠BAC=100°，AB的垂直平分线DE分别交AB、BC于点D、E，则∠BAE=（）A．80° B．60° C．50° D．40°【考点】线段垂直平分线的性质；等腰三角形的性质．【分析】首先利用三角形的内角和定理和等腰三角形的性质∠B，利用线段垂直平分线的性质易得AE=BE，∠BAE=∠B．【解答】解：∵AB=AC，∠BAC=100°，∴∠B=∠C=（180°﹣100°）÷2=40°，∵DE是AB的垂直平分线，∴AE=BE，∴∠BAE=∠B=40°，故选D．【点评】本题主要考查了等腰三角形的性质，三角形的内角和定理，线段垂直平分线的性质，掌握垂直平分线上任意一点，到线段两端点的距离相等和等边对等角是解答此题的关键．5．如图，△ABC中，AB=5，AC=6，BC=4，边AB的垂直平分线交AC于点D，则△BDC的周长是（）A．8 B．9 C．10 D．11【考点】线段垂直平分线的性质．【分析】由ED是AB的垂直平分线，可得AD=BD，又由△BDC的周长=DB+BC+CD，即可得△BDC的周长=AD+BC+CD=AC+BC．【解答】解：∵ED是AB的垂直平分线，∴AD=BD，∵△BDC的周长=DB+BC+CD，∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10．故选C．【点评】本题考查了线段垂直平分线的性质，三角形周长的计算，掌握转化思想的应用是解题的关键．6．如图，在Rt△ABC中，∠C=90°，AB的垂直平分线交AC于点D，交AB于点E．若BC=2，AC=4，则BD=（）A．B．2 C．D．3【考点】线段垂直平分线的性质；勾股定理．【分析】设BD=x，先根据线段垂直平分线的性质可得BD=AD=x，则CD=4﹣x，然后在△BCD中根据勾股定理列出关于x的方程，解方程即可求得BD的长．【解答】解：设BD=x，∵AB垂直平分线交AC于D，∴BD=AD=x，∵AC=4，∴CD=AC﹣AD=4﹣x，在△BCD中，根据勾股定理得x2=22+（4﹣x）2，解得x=．故选C．【点评】本题考查了线段垂直平分线的性质：线段垂直平分线上任意一点，到线段两端点的距离相等，同时考查了勾股定理．7．如图，地面上有三个洞口A、B、C，老鼠可以从任意一个洞口跑出，猫为能同时最省力地顾及到三个洞口（到A、B、C三个点的距离相等），尽快抓到老鼠，应该蹲守在（）A．△ABC三边垂直平分线的交点B．△ABC三条角平分线的交点C．△ABC三条高所在直线的交点D．△ABC三条中线的交点【考点】线段垂直平分线的性质．【专题】应用题．【分析】根据题意，知猫应该到三个洞口的距离相等，则此点就是三角形三边垂直平分线的交点．【解答】解：∵三角形三边垂直平分线的交点到三个顶点的距离相等，∴猫应该蹲守在△ABC三边垂直平分线的交点处．故选A．【点评】此题考查了三角形的外心的概念和性质．熟知三角形三边垂直平分线的交点到三个顶点的距离相等，是解题的关键．8．如图，在△ABC中AB的垂直平分线交AB于点D，交线段BC于点E．BC=6，AC=5，则△ACE的周长是（）A．14 B．13 C．12 D．11【考点】线段垂直平分线的性质．【专题】计算题．【分析】根据线段垂直平分线的性质得AE=BE，然后利用等线段代换即可得到△ACE的周长=AC+BC，再把BC=6，AC=5代入计算即可．【解答】解：∵DE垂直平分AB，∴AE=BE，∴△ACE的周长=AC+CE+AE=AC+CE+BE=AC+BC=5+6=11．故选D．【点评】本题考查了线段垂直平分线的性质：垂直平分线垂直且平分其所在线段；垂直平分线上任意一点，到线段两端点的距离相等．9．如图，在△ABC 中，∠A=36°，AB=AC ，AB 的垂直平分线OD 交AB 于点O ，交AC 于点D ，连接BD ，下列结论错误的是（ ）A ．∠C=2∠AB ．BD 平分∠ABCC ．S △BCD =S △BOD D ．点D 为线段AC 的黄金分割点【考点】线段垂直平分线的性质；等腰三角形的性质；黄金分割．【分析】求出∠C 的度数即可判断A ；求出∠ABC 和∠ABD 的度数，求出∠DBC 的度数，即可判断B ；根据三角形面积即可判断C ；求出△DBC ∽△CAB ，得出BC 2=BC •AC ，求出AD=BC ，即可判断D ．【解答】解：A 、∵∠A =36°，AB=AC ，∴∠C=∠ABC=72°，∴∠C=2∠A ，正确，B 、∵DO 是AB 垂直平分线，∴AD=BD ，∴∠A=∠ABD=36°，∴∠DBC=72°﹣36°=36°=∠ABD ，∴BD是∠ABC的角平分线，正确，C，根据已知不能推出△BCD的面积和△BOD面积相等，错误，D、∵∠C=∠C，∠DBC=∠A=36°，∴△DBC∽△CAB，∴=，∴BC2=CD•AC，∵∠C=72°，∠DBC=36°，∴∠BDC=72°=∠C，∴BC=BD，∵AD=BD，∴AD=BC，∴AD2=CD•AC，即点D是AC的黄金分割点，正确，故选C．【点评】本题考查了相似三角形的性质和判定，等腰三角形性质，黄金分割点，线段垂直平分线性质的应用，主要考查学生的推理能力．10．如图，在△ABC中，AB=AC，∠A=120°，BC=6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为（）A．4cm B．3cm C．2cm D．1cm【考点】线段垂直平分线的性质；等边三角形的判定与性质．【专题】压轴题．【分析】连接AM、AN、过A作AD⊥BC于D，求出AB、AC值，求出BE、CF值，求出BM、CN值，代入MN=BC﹣BM﹣CN求出即可．【解答】解：连接AM、AN、过A作AD⊥BC于D，∵在△ABC中，AB=AC，∠A=120°，BC=6cm，∴∠B=∠C=30°，BD=CD=3cm，∴AB==2cm=AC，∵AB的垂直平分线EM，∴BE=AB=cm同理CF=cm，∴BM==2cm，同理CN=2cm，∴MN=BC﹣BM﹣CN=2cm，故选C．【点评】本题考查了线段垂直平分线性质，等腰三角形的性质，含30度角的直角三角形性质，解直角三角形等知识点的应用，主要考查学生综合运用性质进行推理和计算的能力．11．如图，在△ABC中，AB=AC，∠A=40°，AB的垂直平分线交AB于点D，交AC于点E，连接BE，则∠CBE的度数为（）A．70° B．80° C．40° D．30°【考点】线段垂直平分线的性质；等腰三角形的性质．【专题】几何图形问题．【分析】由等腰△ABC中，AB=AC，∠A=40°，即可求得∠ABC的度数，又由线段AB的垂直平分线交AB于D，交AC于E，可得AE=BE，继而求得∠ABE的度数，则可求得答案．【解答】解：∵等腰△ABC中，AB=AC，∠A=40°，∴∠ABC=∠C==70°，∵线段AB的垂直平分线交AB于D，交AC于E，∴AE=BE，∴∠ABE=∠A=40°，∴∠CBE=∠ABC﹣∠ABE=30°．故选：D．【点评】此题考查了线段垂直平分线的性质以及等腰三角形的性质．此题难度不大，注意掌握数形结合思想的应用．12．如图，在△ABC中，AC=4cm，线段AB的垂直平分线交AC于点N，△BCN的周长是7cm，则BC的长为（）A．1cm B．2cm C．3cm D．4cm【考点】线段垂直平分线的性质．【分析】首先根据MN是线段AB的垂直平分线，可得AN=BN，然后根据△BCN的周长是7cm，以及AN+NC=AC，求出BC的长为多少即可．【解答】解：∵MN是线段AB的垂直平分线，∴AN=BN，∵△BCN的周长是7cm，∴BN+NC+BC=7（cm），∴AN+NC+BC=7（cm），∵AN+NC=AC，∴AC+BC=7（cm），又∵AC=4cm，∴BC=7﹣4=3（cm）．故选：C．【点评】此题主要考查了线段垂直平分线的性质和应用，要熟练掌握，解答此题的关键是要明确：①垂直平分线垂直且平分其所在线段．②垂直平分线上任意一点，到线段两端点的距离相等．③三角形三条边的垂直平分线相交于一点，该点叫外心，并且这一点到三个顶点的距离相等．13．如图，在Rt△ABC中，∠ACB=60°，DE是斜边AC的中垂线，分别交AB、AC于D、E两点．若BD=2，则AC的长是（）A．4 B．4 C．8 D．8【考点】线段垂直平分线的性质；含30度角的直角三角形；勾股定理．【分析】求出∠ACB，根据线段垂直平分线求出AD=CD，求出∠ACD、∠DCB，求出CD、AD、AB，由勾股定理求出BC，再求出AC即可．【解答】解：如图，∵在Rt△ABC中，∠ACB=60°，∴∠A=30°．∵DE垂直平分斜边AC，∴AD=CD，∴∠A=∠ACD=30°，∴∠DCB=60°﹣30°=30°，∵BD=2，∴CD=AD=4，∴AB=2+4=6，在△BCD中，由勾股定理得：CB=2，在△ABC中，由勾股定理得：AC==4，故选：B．【点评】本题考查了线段垂直平分线，含30度角的直角三角形，等腰三角形的性质，三角形的内角和定理等知识点的应用，主要考查学生运用这些定理进行推理的能力，题目综合性比较强，难度适中．14．如图，锐角三角形ABC中，直线L为BC的中垂线，直线M为∠ABC的角平分线，L与M相交于P点．若∠A=60°，∠ACP=24°，则∠ABP的度数为何？（）A．24° B．30° C．32° D．36°【考点】线段垂直平分线的性质．【分析】根据角平分线的定义可得∠ABP=∠CBP，根据线段垂直平分线上的点到两端点的距离相等可得BP=CP，再根据等边对等角可得∠CBP=∠BCP，然后利用三角形的内角和等于180°列出方程求解即可．【解答】解：∵直线M为∠ABC的角平分线，∴∠ABP=∠CBP．∵直线L为BC的中垂线，∴BP=CP，∴∠CBP=∠BCP，∴∠ABP=∠CBP=∠BCP，在△ABC中，3∠ABP+∠A+∠ACP=180°，即3∠ABP+60°+24°=180°，解得∠ABP=32°．故选：C．【点评】本题考查了线段垂直平分线上的点到两端点的距离相等的性质，角平分线的定义，三角形的内角和定理，熟记各性质并列出关于∠ABP的方程是解题的关键．二、填空题15．点P在线段AB的垂直平分线上，PA=7，则PB= 7 ．【考点】线段垂直平分线的性质．【分析】根据线段垂直平分线的性质得出PA=PB，代入即可求出答案．【解答】解：∵点P在线段AB的垂直平分线上，PA=7，∴PB=PA=7，故答案为：7．【点评】本题考查了对线段垂直平分线性质的应用，注意：线段垂直平分线上的点到线段两个端点的距离相等．16．等腰△ABC的底角为72°，腰AB的垂直平分线交另一腰AC于点E，垂足为D，连接BE，则∠EBC的度数为36°．【考点】线段垂直平分线的性质；等腰三角形的性质．【分析】首先根据等腰三角形的性质可得∠A的度数，再根据线段垂直平分线的性质可得AE=BE，进而可得∠ABE=∠A=36°，然后可计算出∠EBC的度数．【解答】解：∵等腰△ABC的底角为72°，∴∠A=180°﹣72°×2=36°，∵AB的垂直平分线DE交AC于点E，∴AE=BE，∴∠ABE=∠A=36°，∴∠EBC=∠ABC﹣∠ABE=36°．故答案为：36°．【点评】此题主要考查了线段垂直平分线的性质，以及等腰三角形的性质，关键是掌握等边对等角．17．如图，在等腰三角形ABC中，AB=AC，DE垂直平分AB，已知∠ADE=40°，则∠DBC= 15 °．【考点】线段垂直平分线的性质；等腰三角形的性质．【分析】根据线段垂直平分线求出AD=BD，推出∠A=∠ABD=50°，根据三角形内角和定理和等腰三角形性质求出∠ABC，即可得出答案．【解答】解：∵DE垂直平分AB，∴AD=BD，∠AED=90°，∴∠A=∠ABD，∵∠ADE=40°，∴∠A=90°﹣40°=50°，∴∠ABD=∠A=50°，∵AB=AC，∴∠ABC=∠C=（180°﹣∠A）=65°，∴∠DBC=∠ABC﹣∠ABD=65°﹣50°=15°，故答案为：15．【点评】本题考查了等腰三角形的性质，线段垂直平分线性质，三角形内角和定理的应用，能正确运用定理求出各个角的度数是解此题的关键，难度适中．18．如图，在△ABC中，∠C=31°，∠ABC的平分线BD交AC于点D，如果DE垂直平分BC，那么∠A= 87 °．【考点】线段垂直平分线的性质．【分析】根据DE垂直平分BC，求证∠DBE=∠C，再利用角平分线的性质和三角形内角和定理，即可求得∠A的度数．【解答】解：∵在△ABC中，∠C=31°，∠ABC的平分线BD交AC于点D，∴∠DBE=∠ABC=（180°﹣31°﹣∠A）=（149°﹣∠A），∵DE垂直平分BC，∴BD=DC，∴∠DBE=∠C，∴∠DBE=∠ABC=（149°﹣∠A）=∠C=31°，∴∠A=87°．故答案为：87．【点评】此题本题考查的知识点为线段垂直平分线的性质，关键是根据角平分线的性质，三角形内角和定理等知识点进行分析．19．如图，△ABC中，DE是BC的垂直平分线，DE交AC于点E，连接BE．若BE=9，BC=12，则cosC= ．【考点】线段垂直平分线的性质；解直角三角形．【分析】根据线段垂直平分线的性质，可得出CE=BE，再根据等腰三角形的性质可得出CD=BD，从而得出CD：CE，即为cosC．【解答】解：∵DE是BC的垂直平分线，∴CE=BE，∴CD=BD，∵BE=9，BC=12，∴CD=6，CE=9，∴cosC===，故答案为．【点评】本题考查了线段垂直平分线的性质以及等腰三角形的性质．此题难度不大，注意掌握数形结合思想的应用．20．已知点P在线段AB的垂直平分线上，PA=6，则PB= 6 ．【考点】线段垂直平分线的性质．【分析】直接根据线段垂直平分线的性质进行解答即可．【解答】解：∵点P在线段AB的垂直平分线上，PA=6，∴PB=PA=6．故答案为：6．【点评】本题考查的是线段垂直平分线的性质，熟知垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．21．如图，△ABC中，AB+AC=6cm，BC的垂直平分线l与AC相交于点D，则△ABD的周长为 6 cm．【考点】线段垂直平分线的性质．【专题】数形结合．【分析】根据中垂线的性质，可得DC=DB，继而可确定△ABD的周长．【解答】解：∵l垂直平分BC，∴DB=DC，∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=6cm．故答案为：6．【点评】本题考查了线段垂直平分线的性质，注意掌握线段垂直平分线上任意一点，到线段两端点的距离相等．22．如图，△ABC中，∠A=40°，AB的垂直平分线MN交AC于点D，∠DBC=30°，若AB=m，BC=n，则△DBC的周长为m+n ．【考点】线段垂直平分线的性质；三角形内角和定理；等腰三角形的性质．【分析】根据线段垂直平分线性质得出AD=BD，推出∠A=∠ABD=40°，求出∠ABC=∠C，推出AC=AB=m，求出△DBC的周长是DB+BC+CD=BC+AD+DC=AC+BC，代入求出即可．【解答】解：∵AB的垂直平分线MN交AC于点D，∠A=40°，∴AD=BD，∴∠A=∠ABD=40°，∵∠DBC=30°，∴∠ABC=40°+30°=70°，∠C=180°﹣40°﹣40°﹣30°=70°，∴∠ABC=∠C，∴AC=AB=m，∴△DBC的周长是DB+BC+CD=BC+AD+DC=AC+BC=m+n，故答案为：m+n．【点评】本题考查了三角形内角和定理，线段垂直平分线性质，等腰三角形的性质的应用，注意：线段垂直平分线上的点到线段两个端点的距离相等．23．如图，在▱ABCD中，AB=3，BC=5，对角线AC、BD相交于点O，过点O作OE⊥AC，交AD于点E，连接CE，则△CDE的周长为8 ．【考点】线段垂直平分线的性质；平行四边形的性质．【专题】几何图形问题．【分析】根据平行四边形的性质，得知AO=OC，由于OE⊥AC，根据线段垂直平分线的性质，可知AE=EC，则△CDE的周长为CD与AD之和，即可得解．【解答】解：根据平行四边形的性质，∴AO=OC，∵OE⊥AC，∴OE为AC的垂直平分线，∴AE=EC，∴△CDE的周长为：CD+AD=5+3=8，故答案为：8．【点评】本题考查了平行四边形的性质以及线段垂直平分线的性质，熟记各性质与定理是解题的关键．。

教学目标1.了解轴对称图形、两个图形成轴对称这两个概念之间的联系和区别2.经历丰富材料的学习过程，发展对图形的观察、分析、判断、归纳等能力重难点导航通过具体的轴对称图形实例,让学生经历观察、比较、分析等数学活动,从而让学生认识轴对称图形,知道轴对称与轴对称图形之间的区别,而后通过线段与角等轴对称图形加深对轴对称图形的理解（一）轴对称与轴对称图形一、轴对称与轴对称图形把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么称这两个图形关于这条直线对称，也称这两个图形成轴对称，这条直线叫做对称轴，两个图形中的对应点叫做对称点.把一个图形沿着某一条直线折叠，如果直线两旁的部分能够互相重合，那么称这个图形是轴对称图形，这条直线就是对称轴.二.轴对称与轴对称图形的区别与联系如果把成轴对称的两个图形看成一个整体，那么这个整体就是一个；如果把一个轴对称图形位于轴对称两旁的部分看成两个图形，那么这两部分就成 .例1．如图，由４个全等的正方形组成L形图案，（１）请你在图案中改变1个正方形的位置，使它变成轴对称图案。

（２）请你在图中再添加一个小正方形，使它变成轴对称图案。

（1）（2）例2．（开放型问题）如图①是由三个小正方形组成的体验.请你在图中②～⑤上分别补画一个小正方形，使补画后的图形为轴对称图形.①②③④⑤（二）轴对称的性质一、线段垂直平分线的概念垂直并平分一条线段的直线，叫作这条直线的垂直平分线.二、轴对称的性质成轴对称的两个图形中，对应点的连线被对称轴垂直平分.例1:如图，两片树叶成轴对称，请你画出它们的对称轴.三、利用轴对称的性质作轴对称图形画一个图形关于一条直线对称的图形，关键是确定某些点关于这条直线的对称轴.往往按照下面的步骤.1.画轴对称图形，首先应确定对称轴，然后找出对称点.2.画已知线段关于某条直线的对称线段，或画已知三角形（四边形）关于某条直线对称的三角形（四边形），关键在于画出已知线段的各端点或已知三角形（四边形）的各顶点关于这条直线的对称点.例3：如图，四边形CDEF是一个长方形台球桌面的示意图，白、黑两球分别位于点A、B处，试问怎样撞击白球A，可以使白球A先碰到桌边DE，再反弹击中黑球B？例4：如图a是一张长方形纸带，∠DEF=20°，将纸带沿EF折叠（如图b），再沿BF折叠（如图c）则图中∠CFE的度数是例5：如图①，在3×3的正方形网格中，已有两个小正方形被涂色，再将图中其余的任意一个小正方形涂色，使整个图案构成一个轴对称图形的方法有种．（三）线段、角的轴对称性一、线段垂直平分线的性质1、线段是轴对称图形，线段的垂直平分线是它的对称轴2、线段垂直平分线上的点到线段两端的距离相等3、到线段两端距离相等的点在这条线段AB的垂直平分线上二、角是轴对称图形，它的对称轴是它的角平分线。

教学主题轴对称期中复习教学目标巩固轴对称易考题型重要知识点1.轴对称2.线段、角的轴对称性3.等腰三角形的轴对称性教学过程知识点一、轴对称图形1、下列图案是几种名车的标志，请你从中判断哪些是轴对称图形，并画出其对称轴．2、下列图形中，轴对称图形的个数是( )A．1 B．2 C．3 D．4知识点二、线段轴对称性1.线段垂直平分线的性质定理：线段垂直平分线上的点_____________________.2.线段垂直平分线的性质定理的逆定理：到线段两端距离相等的点 .例题：1．下列图形中，不是轴对称图形的是 ( )A．两条相交直线 B．线段C．有公共端点的两条相等线段 D．有公其端点的两条不相等线段2．到三角形的三个顶点距离相等的点是 ( )A．三条角平分线的交点 B．三条中线的交点C．三条高的交点 D．三条边的垂直平分线的交点3..如图，在△ABC中，AB＝a，AC＝b，BC边上的垂直平分线DE分别交BC、BA于点D、E，则△AEC的周长等于 ( )A．a＋b B．a－b C．2a＋b D．a＋2b4.如图，三角形纸片ABC，AB＝10 cm，BC＝7 cm，AC＝6 cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为_______cm；连接CE，则线段BD、CE的关系是__________________________________．知识点三、角的轴对称性角平分线上的点到角的两边距离___________.到角两边距离相等的点在___________.例题：1.如图，AD∥BC，DC⊥AD，AE平分∠BAD，且E是DC的中点，EF⊥AB于点F．问AD、BC与AB之间有何关系?为什么?2.如图，已知BD为∠ABC的平分线，DE⊥BC于E，且AB+BC=2BE(1) 求证：∠BAD+∠BCD=180°；(2) 若将条件“AB+BC=2BE”与结论“∠BAD+∠BCD=180°”互换，结论还成立吗?请说明理由知识点四、等腰三角形的轴对称性1、定理：等腰三角形的两底角相等（简称“等边对等角”）.2、定理：等腰三角形底边上的高线、中线及角平分线重合.3.等边三角形的判定方法：（1）___________________三角形是等边三角形；（2）定理：_____________________三角形是等边三角形；（3）定理：有一个角是______0的等腰三角形是等边三角形.4、直角三角形斜边上的中线等于斜边的一半。

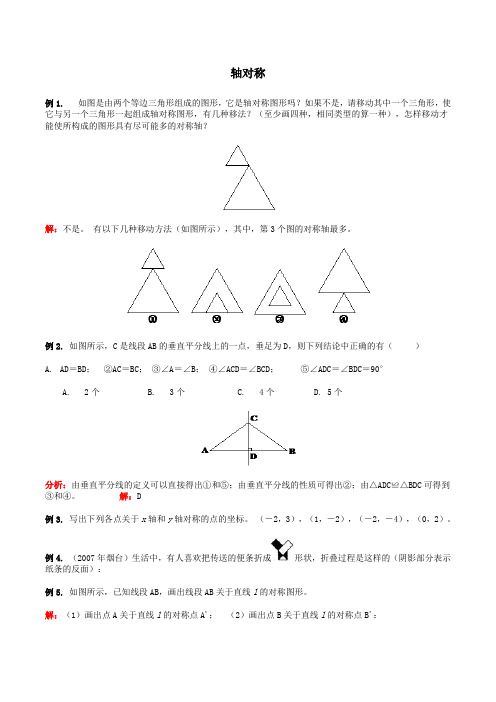
轴对称例1.如图是由两个等边三角形组成的图形，它是轴对称图形吗？如果不是，请移动其中一个三角形，使它与另一个三角形一起组成轴对称图形，有几种移法？（至少画四种，相同类型的算一种），怎样移动才能使所构成的图形具有尽可能多的对称轴？解：不是。

有以下几种移动方法（如图所示），其中，第3个图的对称轴最多。

例2. 如图所示，C是线段AB的垂直平分线上的一点，垂足为D，则下列结论中正确的有（）A.AD＝BD；②AC＝BC；③∠A＝∠B；④∠ACD＝∠BCD；⑤∠ADC＝∠BDC＝90°A. 2个B. 3个C. 4个D. 5个分析：由垂直平分线的定义可以直接得出①和⑤；由垂直平分线的性质可得出②；由△ADC≌△BDC可得到③和④。

解：D例3. 写出下列各点关于x轴和y轴对称的点的坐标。

（－2，3），（1，－2），（－2，－4），（0，2）。

例4.（2007年烟台）生活中，有人喜欢把传送的便条折成形状，折叠过程是这样的（阴影部分表示纸条的反面）：例5. 如图所示，已知线段AB，画出线段AB关于直线l的对称图形。

解：（1）画出点A关于直线l的对称点A'；（2）画出点B关于直线l的对称点B'：（3）连结A'B'，则线段A'B'即为所求。

例6.要在河边修建一个水泵站，分别向张村、李庄送水（如图）。

修在河边什么地方，可使所用水管最短？解：设张村为点A，李庄为点B，张村和李庄这一侧的河岸为直线l。

（1）作点B关于直线l的对称点，（2）连结，交直线l于点C，点C就是所求的水泵站的位置。

（如图所示）1. 下列说法错误的是（）A. 关于某直线对称的两个图形一定能完全重合B. 全等的两个三角形一定关于某直线对称C. 轴对称图形的对称轴至少有一条D. 线段是轴对称图形2. 轴对称图形的对称轴是（）A. 直线B. 线段C. 射线D. 以上都有可能3. 下面各组点关于y轴对称的是（）A. （0，10）与（0，－10）B. （－3，－2）与（3，－2）C. （－3，－2）与（3，2）D. （－3，－2）与（－3，2）*4. 下列图形中，不是轴对称图形的是（）A. 一条线段B. 两条相交直线C. 有公共端点的两条相等的线段D. 有公共端点的两条不相等的线段5. （2007年河南）如图，ΔABC与ΔA'B'C'关于直线l对称，则∠B的度数为（）A. 30°B. 50°C. 90°D. 100°6. （2008年江苏苏州）下列图形中，是轴对称图形的是（）*7. （2008年武汉）如图，六边形ABCDEF是轴对称图形，CF所在的直线是它的对称轴，若∠AFC＋∠BCF ＝150°，则∠AFE＋∠BCD的大小是（）A. 150°B. 300°C. 210°D. 330°**8. （2008年全国数学竞赛浙江预赛）如图，直线l1与直线l2相交，∠α＝60°，点P在∠α内（不在l1，l2上）。

第十三章《轴对称》一、知识点归纳（一）轴对称和轴对称图形1、有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点．两个图形关于直线对称也叫做轴对称．2、轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

（对称轴必须是直线）3、对称点：折叠后重合的点是对应点，叫做对称点。

4、轴对称图形的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

类似的，轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

连接任意一对对应点的线段被对称轴垂直平分．轴对称图形上对应线段相等、对应角相等。

5．画一图形关于某条直线的轴对称图形步骤：找到关键点，画出关键点的对应点，按照原图顺序依次连接各点。

（二）、轴对称与轴对称图形的区别和联系区别：轴对称是指两个图形之间的形状与位置关系，成轴对称的两个图形是全等形；轴对称图形是一个具有特殊形状的图形，把一个轴对称图形沿对称轴分成两个图形，这两个图形是全等形，并且成轴对称．联系：1：都是折叠重合2;如果把成轴对称的两个图形看成一个图形那么他就是轴对称图形，反之亦然。

（三）线段的垂直平分线（1）经过线段的中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线（或线段的中垂线）（2）线段的垂直平分线上的点与这条线段两个端点的距离相等；反过来，与一条线段两个端点距离相等的点在这条线段的垂直平分线上．（证明是必须有两个点）因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合．（四）用坐标表示轴对称1、点（x，y）关于x轴对称的点的坐标为（-x，y）；2、点（x，y）关于y轴对称的点的坐标为（x，-y）；(五）关于坐标轴夹角平分线对称点P（x，y）关于第一、三象限坐标轴夹角平分线y＝x对称的点的坐标是（y，x）点P（x，y）关于第二、四象限坐标轴夹角平分线y＝－x对称的点的坐标是（－y，－x）（六）关于平行于坐标轴的直线对称点P（x，y）关于直线x＝m对称的点的坐标是（2m－x，y）；点P（x，y）关于直线y＝n对称的点的坐标是（x，2n－y）；(七）等腰三角形1、等腰三角形性质：性质1：等腰三角形的两个底角相等（简写成“等边对等角”）性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。

数学八（上）1.4《线段、角的轴对称性》习题
1.在等腰三角形中，顶角的顶点一定在底边的垂直平分线上吗？请说明理由。

答案：1.顶角的顶点一定在底边的垂直平分线上。

因为等腰三角形的两腰相等，根据到线段两端距离相等的点在线段的
垂直平分线上，所以顶点一定在底边的垂直平分线上。

2.（1）利用网格线画出图中四边形ABCD的任意联邦的垂直平分线，设它们相交
于点O；
（2）观察点O是否在另两边的垂直平分线上；
（3）如果将图中的四边形的顶点D向左移动8格，还能观察到与上面相同的结论吗？
答案：（1）略；（2）在；（3）不能
3.如图，在△ABC中，BC=7，AB 的垂直平分线分别交AB、BC于点D、E、AC的
垂直平分线分别交于AC、BC于点F、G，求△AEG的周长。

答案：3.因为点E在AB的垂直平分线上，所以EA=EB.同理 GA=GC。

△AEC的周长=AE+EG+AG=BE+EG+GC=BC=7
4.（1）利用网络线画出图中四边形ABCD的任意两个内角的平分线，设它们相交
于点O；
（2）观察点O是否在另两个内角的平分线上。

答案：（1）略
（2）在
5.如图，已知△ABC。

（1）用直尺和圆规分别作∠A和∠B平分线，设它们相交于点O；
（2）点O在∠C的平分线上吗？试说明理由。

（第5题答案）
答案：5.（1）略
（2）在。

过点O分别作OD⊥AC,OE⊥BC,OF⊥AB,垂足分别为D、E、F。

因为点O在∠CAB的角平分线上，OD⊥AC,OF⊥AB,
所以OD=OF.同理 OE=OF.因此OD=OE。

所以点O在∠C的平分线上。

教学内容轴对称的性质、线段的轴对称性教学目标会做轴对称图形、掌握线段的轴对称性质、会求线段和最小值重点线段的轴对称性质、求线段和最小值课堂精讲【知识梳理】1、轴对称图形相对一个图形的对称而言；轴对称是关于直线对称的两个图形而言。

2、轴对称的性质：①轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线；②如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连的线段的垂直平分线；题型一、判断轴对称图形及对称轴数量1、下面四个手机应用图标中是轴对称图形的是（）A．B．C．D．2、倡导节约，进入绿色，节约型社会，在食品包装、街道、宣传标语上随处可见节能、回收、绿色食品、节水的标志，在这些标志中，是轴对称图形的是（）A．B．C．D．3、如图所示的图形分别有几条对称轴?请分别画出它们的对称轴.4、若下列选项中的图形均为正多边形，则哪一个图形恰有4条对称轴？（）A．B． C．D．题型二、做轴对称图形1、如图，作出ABC关于BC所在直线对称的图形.2、作出△ABC关于直线m的对称图形．3、如图，在平面直角坐标系中，△ABC的顶点A（0，1），B（3，2），C（1，4）均在正方形网格的格点上．画出△ABC关于x轴的对称图形△A1B1C1；4、如图是4×4正方形网格，其中已有3个小正方形涂成了黑色，现在要从其余13个白色小方格中选出一个也涂成黑色的图形称为轴对称图形，这样的白色小方格有（）A．2个B．3个C．4个D．5个5、如图，由4个小正方形组成的田字格中，△ABC的顶点都是小正方形的顶点，则田字格上画与△ABC成轴对称的三角形，且顶点都是小正方形的顶点，则这样的三角形（不包含△ABC本身）共有（）A．1个B．3个C．2个D．4个题型三、线段的轴对称的性质1、线段的垂直平分线：①性质定理：线段的垂直平分线上的点到线段的两个端点的距离相等；②判定定理：到一条线段两个端点的距离相等的点在这条线段的垂直平分线上。

八年级数学线段和角的轴对称性Prepared on 21 November 2021线段、角的轴对称性[知识要点]1.线段的垂直平分线性质定理：线段的垂直平分线上的点到线段两端的距离相等。

判定定理：到线段两端的距离相等的点在这条线段的垂直平分线上。

2.角平分线性质定理：角平分线上任意一点到角的两边的距离相等。

判定定理：到角的两边距离相等的点在这个角的平分线上。

3.尺规作图作线段的垂直平分线和角的平分线[点睛例题]例1.如图，C是∠AOB内一点，C1、C2分别是点C关于OA、OB的对称点，若C1、C2的连线交OA于D，交OB于E，C1C2＝4.5cm，则△CDE的周长为（）A．4.5cm B．6.5cm C．5.5cmD．无法求例2.如图，在△ABC中，点O是∠ABC的平分线与线段BC的垂直平分线的交点，则下列结论不一定成立的是（）A．OB＝OC B．OD＝OF C．OA＝OB＝OC D．BD＝DC例3.如图，A、B、C是新建的三个居民小区，我们已经在到三个小区距离相等的地方修建了一所学校，现规划修建居民小区D，其要求是：（1）到学校的距离与其它小区到学校的距离一样；（2）控制人口密度，有利于生态环境建设，试确定居民小区D的位置．[点睛习题]1、如图，等腰△ABC的周长为21，底边BC=5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为（）A．13 B．14 C．15 D．162、已知，如图，△ABC中，∠ABC与∠ACB的平分线交于点P，那么点P是否在∠BAC的平分线上为什么3、下列说法：（1）若直线PE是线段AB的中垂线，则EA＝EB，PA＝PB；（2）若EA＝EB，PA＝PB，则直线PE垂直平分线段AB；（3）若PA＝PB，则点P必是线段AB的中垂线上的点；（4）若AE＝BE，则经过点E的直线垂直平分线AB，其中正确的个数为（）A．1个B．2个C．3个D．4个4、已知，如图，△ABC的两个外角的平分线交于点P，那么点P是否在∠BAC的平分线上为什么5.如图，△ABC中，DE垂直平分AC交AB于E，∠A＝30°，∠ACB＝80°，则∠BCE＝____°。

第十三章《轴对称》一、知识点归纳（一）轴对称和轴对称图形1、有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点．两个图形关于直线对称也叫做轴对称．2、轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

（对称轴必须是直线）3、对称点：折叠后重合的点是对应点，叫做对称点。

4、轴对称图形的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

类似的，轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

连接任意一对对应点的线段被对称轴垂直平分．轴对称图形上对应线段相等、对应角相等。

5．画一图形关于某条直线的轴对称图形步骤：找到关键点，画出关键点的对应点，按照原图顺序依次连接各点。

（二）、轴对称与轴对称图形的区别和联系区别：轴对称是指两个图形之间的形状与位置关系，成轴对称的两个图形是全等形；轴对称图形是一个具有特殊形状的图形，把一个轴对称图形沿对称轴分成两个图形，这两个图形是全等形，并且成轴对称．联系：1：都是折叠重合2;如果把成轴对称的两个图形看成一个图形那么他就是轴对称图形，反之亦然。

（三）线段的垂直平分线（1）经过线段的中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线（或线段的中垂线）（2）线段的垂直平分线上的点与这条线段两个端点的距离相等；反过来，与一条线段两个端点距离相等的点在这条线段的垂直平分线上．（证明是必须有两个点）因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合．（四）用坐标表示轴对称1、点（x，y）关于x轴对称的点的坐标为（-x，y）；2、点（x，y）关于y轴对称的点的坐标为（x，-y）；(五）关于坐标轴夹角平分线对称点P（x，y）关于第一、三象限坐标轴夹角平分线y＝x对称的点的坐标是（y，x）点P（x，y）关于第二、四象限坐标轴夹角平分线y＝－x对称的点的坐标是（－y，－x）（六）关于平行于坐标轴的直线对称点P（x，y）关于直线x＝m对称的点的坐标是（2m－x，y）；点P（x，y）关于直线y＝n对称的点的坐标是（x，2n－y）；(七）等腰三角形1、等腰三角形性质：性质1：等腰三角形的两个底角相等（简写成“等边对等角”）性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。

第十三章轴对称、知识框架:二、知识概念：1.基本概念：⑴轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合， 这个图形就叫做轴对称图形•⑵两个图形成轴对称：把一个图形沿某一条直线折叠， 如果它能够与另一个图形重合， 那么就说这两个图形关于这条直线对称 •铀对称图形AA\L区別只对f —冲-)ft-fKmr150对裤轴CF 一佥只冇一舉>(“轴对称旳睛(WK 予秤瓚的俭M 工菲.矗麹»JSt :t 鹽个、曲擢： 心)只有1一頭〉对務柄联系却晁把射对材囲宼泊对禅轴 曲卿撷甘"么卿牛曲癣 轶夭于迭条 W 鑽處抽对耕-如杲把.阿十庇抽对秤的国招 拼& — 妊呑虑一* 益林.外 也亡赣足一亍轴对STSJ 搭-(4) 线段的垂直平分线：经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直 平分线• (5) 等腰三角形：有两条边相等的三角形叫做等腰三角形 •相等的两条边叫做腰， 另一条边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫做底角(6) 等边三角形：三条边都相等的三角形叫做等边三角形 2.基本性质：⑴对称的性质：① 不管是轴对称图形还是两个图形关于某条直线对称， 对称轴都是任何一对对应点所连线段的垂直平分线.② 对称的图形都全等•③ 如果两个图形的对应点连线被同条直线垂直平分，那么这两个图形关于这条直线对称。

④ 两个图形关于某条直线成轴对称， 如果它们的对应线段或延长线相交， 那么交点在对称轴上。

⑵线段垂直平分线的性质：① 线段垂直平分线上的点与这条线段两个端点的距离相等 ② 与一条线段两个端点距离相等的点在这条线段的垂直平分线上 ⑶关于坐标轴对称的点的坐标性质①点(x, y )关于x 轴对称的点的坐标为(x, -y ).②点（x, y ）关于y轴对称的点的坐标为（-x, y ）.③点（x, y ）关于原点对称的点的坐标为（-x,- y ）⑷等腰三角形的性质：①等腰三角形两腰相等•②等腰三角形两底角相等（等边对等角）③等腰三角形的顶角角平分线、底边上的中线，底边上的高相互重合•④等腰三角形是轴对称图形，对称轴是三线合一（1条）.⑸等边三角形的性质：①等边三角形三边都相等•②等边三角形三个内角都相等，都等于60 °③等边三角形每条边上都存在三线合一④等边三角形是轴对称图形，对称轴是三线合一（3条）.（6）三角形三条边的垂直平分线相交于一点，这个点到三角形三个顶点的距离相等3.基本判定：⑴等腰三角形的判定：①有两条边相等的三角形是等腰三角形•②如果一个三角形有两个角相等，那么这两个角所对的边也相等（等角对等边）•⑵等边三角形的判定：①三条边都相等的三角形是等边三角形•②三个角都相等的三角形是等边三角形•③有一个角是60°的等腰三角形是等边三角形.4.基本方法：⑴做已知直线的垂线：⑵做已知线段的垂直平分线：⑶作对称轴：连接两个对应点，作所连线段的垂直平分线⑷作已知图形关于某直线的对称图形：⑸在直线上做一点，使它到该直线同侧的两个已知点的距离之和最短•常考例题精选1. （2015 •三明中考）下列图形中，不是轴对称图形的是（）2. （2015 •日照中考）下面所给的交通标志图中是轴对称图形的是（）ABC3. （2015 •杭州中考）下列“表情图”中，属于轴对称图形的是（）4. （2015 •凉山州中考）如图，/ 3=30°,为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时，必须保证/ 1的度数为（）A.30 °B.45 °C.60 °D.755. （2015 •德州中考）如图，动点P从（0，3）出发，沿所示的方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P第2013次碰到矩形的边时，点P的坐标为（）771 ~1 ~2 ~~ ~~6 ~7 d F A.（1，4） B.（5，0） C.（6，4）D.（8，3）6. （2015 •南充中考）如图，△ ABC中, AB=AC Z B=70，则/A的度数是（）A.70 ° B.55C.50 °D.407. （2015 •玉溪中考）若等腰三角形的两边长分别为4和8,贝尼的周长为（）A.12B.16C.20D.16 或208. （2014 •海门模拟）如图，在边长为1的正方形网格中，将△ ABC向右平移两个单位长度得到△ A B' C',则与点B'关于x轴对称的点的坐标是（）A.（0，-1） B.（1，1） C.（2，-1）D.（1，-1）9. （2015 •绵阳中考）如图，AC BD相交于O, AB// DC AB=BC / D=40，/ ACB= 35°，则/ AOD= ______ .10. （2015 •丽水中考）如图，在等腰厶ABC中，AB=AC Z BAC=50，/ BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合，则/ CEF的度数1. （2015遵义）观察下列图形，是轴对称图形的是（）2. 点P（5，—4）关于y轴的对称点是（）A. （5，4）B. （5，—4）C. （4，—5）D. （—5，—4）3. 如图，△ ABC与厶ADC关于AC所在的直线对称，/ BCD= 70° ，/ BA B C D=80°，则/ DAC的度数为（）D. 854. 如图，在Rt A ABC 中，/ C= 90° ，/ B = 15° ，DE 垂直平分AB 交BC于点E，BE = 4，则AC长为（），第4题图）A. 2B. 3C. 4 D .以上都不对6. 如图是一台球桌面示意图，图中小正方形的边长均相等，黑球放在如图 所示的位置，经白球撞击后沿箭头方向运动，经桌边反弹最后进入球洞的序号是8. 如图，D ABC 内一点，CD 平分Z ACB ，BE 丄CD ，垂足为D ，交AC 于点 E ，Z A ABE ，AC = 5，BC = 3，贝U BD 的长为（）9.如图，已知S A ABC = 12, AD 平分Z BAC ，且AD 丄BD 于点D ，则S ^ADC的值是（ ）5. 如图，AB = AC = AD ,若/ BAD = 80则/ BCD =(C. 140 D . 1607. （2015玉林）如图，在厶ABC正确的是（ ）EC C . 中，AB = AC ，DE // BC ，则下列结论中不 Z ADE = Z C D . DE = *BC，第5题图）(A . 10 B. 8 C . 610. 如图，C为线段AE上一动点（不与点A , E重合）,在AE同侧分别作正三角形ABC和正三角形CDE, AD 与BE交于点O, AD与BC交于点P，BE 与CD交于点Q,连接PQ.以下五个结论：①AD = BE;②PQ// AE ;③AP= BQ; ④DE= DP;⑤/ AOB = 60° .其中正确的结论的个数是（）A. 2个B. 3个C. 4个D. 5个12. 如图，D, E ABC两边AB , AC的中点,将厶ABC沿线段DE折叠，使点A落在点F处，若/ B = 55° ,则/BDF等于____________ .A「，第12题图）13. ____________________________________________________________ 如图，在3X 3的正方形网格中，已有两个小正方形被涂黑，再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的方法有________________________ 种.14. 如图，在厶ABC中，AB = AC , AB的垂直平分线交BC于点D ,垂足15. _______ 在厶ABC中，AC = BC,过点A作厶ABC的高AD ,若/ ACD = 30 贝B = __________ .16. ____ 如图，△ ABC中，D, E分别是AC , AB上的点，BD与CE交于点O. 给出下列三个条件：①/ EBO = /DCO;②/ BEO = /CDO:③BE = CD.上述三个条件中，哪两个条件可判定△ ABC是等腰三角形（用序号写出一种情形）：.，第16题图）17. _________________________ 如图是由9个等边三角形拼成的六边形，若已知中间的小等边三角形的边长是2,则六边形的周长是 .' ，第17题图）18. __ 如图，已知/AOB = 30° ，OC平分/ AOB，在OA上有一点M，OM =10 cm,现要在OC, OA上分别找点Q，N，使QM + QN最小，则其最小值为.，第18题图）19. 如图，某校准备在校内一块四边形草坪内栽上一棵银杏树，要求银杏树的位置点P到边AB，BC的距离相等，并且点P到点A，D的距离也相等.请用尺规作图作出银杏树的位置点P.不写作法，保留作图痕迹）23.如图，△ ABC，△ ADE是等边三角形，B，求证：(1)CE=AC + DC; (2)Z ECD = 60° . C，D在同一直线上.20. 如图，在平面直角坐标系中，A( —2, 2), B( —3, —2).(1) 若点D与点A关于y轴对称，则点D的坐标为__________ ;(2) 将点B先向右平移5个单位再向上平移1个单位得到点C，则点C的坐标为________ ;(3) 求A，B，C，D组成的四边形ABCD的面积.■I r厂m ! I I_ ■i == = Ji1 l:-一十一4二* t： 1 ER I r21. 如图，在厶ABC 中，AB = AC, D 为BC 为上一点，/ B = 30° ，/ DAB45(1) 求/ DAC的度数；(2)求证：DC = AB.22. (2015潜江)我们把两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AB = CB，AD = CD，角或者对角线有关的一个结论，并证明你的结论.请你写出与筝形ABCD的24. 如图,在等腰Rt A ABC中,/ ACB = 90° , D为BC的中点,DE丄AB , 垂足为E,过点B作BF // AC交DE的延长线于点F,连接CF.(1) 求证：AD丄CF;(2) 连接AF ,试判断△ ACF的形状，并说明理由.25. 如图，已知AE丄FE,垂足为E,且E是DC的中点.(1) 如图①，如果FC丄DC, AD丄DC,垂足分别为C, D,且AD = DC,判断AE是/ FAD的角平分线吗？(不必说明理由)(2) 如图②，如果(1)中的条件“ AD = DC”去掉，其余条件不变，⑴中的结论仍成立吗？请说明理由；(3) 如图③，如果⑴的条件改为“ AD // FC” , (1)中的结论仍成立吗？请说明理由.。

八年级数学上册第十三章轴对称经典大题例题单选题1、如图，三条笔直的公路两两相交，交点分别在点A、B、C处，有两户村民分别在点D和点E处，现准备建造一个蓄水池，要求水池到两条公路AB、BC的距离相等，且到两户村民D、E的距离相等，则水池修建的位置应该是（）A．在∠B的平分线与DE的交点处B．在线段AB、AC的垂直平分线的交点处C．在∠B的平分线与DE的垂直平分线的交点处D．在∠A的平分线与DE的垂直平分线的交点处答案：C分析：根据角平分线的性质得到水池修建在∠ABC的平分线上，根据线段的垂直平分线的性质得到水池修建在DE的垂直平分线上，从而可对各选项进行判断．解：作∠ABC的平分线和DE的垂直平分线，它们相交于P点，如图，则水池修建的位置应该为P点．故选：C．小提示：本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等．也考查了线段垂直平分线的性质．2、如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=7，BD是△ABC的角平分线，点P，点N分别是BD，AC边上的动点，点M在BC上，且BM=1，则PM+PN的最小值为（）A．3B．2√3C．3.5D．3√3答案：A分析：作点M关于BD的对称点M′，连接PM′，则PM′=PM，BM=BM′=1，当N，P，M′在同一直线上，且M′N⊥AC时，PN+PM′的最小值等于垂线段M′N的长，利用含30°角的直角三角形的性质，即可得到PM+ PN的最小值．解：如图所示，作点M关于BD的对称点M′，连接PM′，则PM′=PM，BM=BM′=1，∴PN+PM=PN+PM′，当N，P，M′在同一直线上，且M′N⊥AC时，PN+PM′的最小值等于垂线段M′N的长，此时，∵Rt△AM′N中，∠A=30°，∴M′N=12AM′=12(7−1)=3，∴PM+PN的最小值为3，故选择A．小提示：本题主要考查了最短路线问题，30°直角三角形性质，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点．3、若点P (a +1,2−2a )关于x 轴的对称点在第四象限，则a 的取值范围为（ ）A ．a >−1B ．a <1C ．−1<a <1D ．a <−1答案：C分析：根据关于x 轴对称的点，横坐标不变，纵坐标互为相反数，求出对称点，再由第四象限内点的坐标符号为（+，-），据此列不等式解答．解：∵点P (a +1,2−2a )关于x 轴的对称点坐标为（a +1，2a -2），且在第四象限，∴a +1>0，且2a -2<0，解得-1<a <1，故选：C ．小提示：此题考查了轴对称的性质，各象限内点的坐标特点，熟记各象限内点的坐标符号特点是解题的关键．4、将三角形纸片（△ABC ）按如图所示的方式折叠，使点C 落在AB 边上的点D ，折痕为EF ．已知AB =AC =3,BC =4，若以点B 、D 、F 为顶点的三角形与△ABC 相似，那么CF 的长度是（ ）A ．2B ．127或2C ．127D ．125或2答案：B分析：分两种情况：若∠BFD=∠C或若∠BFD=∠A，再根据相似三角形的性质解题∵△ABC沿EF折叠后点C和点D重合，∴FD=CF，设CF=x，则FD=CF=x,BF=4−x，以点B、D、F为顶点的三角形与△ABC相似，分两种情况：①若∠BFD=∠C，则BFBC =FDAC，即4−x4=x3，解得x=127；②若∠BFD=∠A，则BFAB =FDAC，即4−x3=x3，解得x=2．综上，CF的长为127或2，故选：B．小提示：本题考查相似三角形的性质，是重要考点，掌握相关知识是解题关键．5、如图，△ABC中，AB=AC,AD⊥BC于点D，DE⊥AB于点E，BF⊥AC于点F，BF=8，则DE的长为（）A．2B．3C．4D．5答案：C分析：根据等腰三角形的性质可得CD=BD，从而得到S△ABC=2S△ABD，从而得到12AC⋅BF=2×12AB⋅DE，即可求解．解：∵AB=AC,AD⊥BC，∴CD=BD，∴S△ABC=2S△ABD，∵DE⊥AB，BF⊥AC，∴S△ABC=12AC⋅BF,S△ABD=12AB⋅DE，∴12AC⋅BF=2×12AB⋅DE，∵BF=8，∴DE=4．故选：C小提示：本题主要考查了等腰三角形的性质，熟练掌握等腰三角形的性质是解题的关键．6、如图，在Rt△ABC中，∠B＝90°，ED是AC的垂直平分线，交AC于点D，交BC于点E．已知∠C＝7∠BAE，则∠C的度数为（）A．41°B．42°C．43°D．44°答案：B分析：设∠BAE＝x°，则∠C＝7x°，根据ED是AC的垂直平分线，有AE＝EC，即有∠EAC＝∠C＝7x°，根据直角三角形中两锐角互余建立方程，解方程即可求解．设∠BAE＝x°，则∠C＝7x°，∵ED是AC的垂直平分线，∴AE＝EC，∴∠EAC＝∠C＝7x°，∵∠B＝90°，∴∠C+∠BAC＝90°，∴7x+7x+x＝90，解得：x＝6，∴∠C＝7×6°＝42°，故选：B．小提示：本题考查了直角三角形的性质，等腰三角形的性质，线段垂直平分线的性质等知识点，能根据线段垂直平分线性质求出AE＝CE是解此题的关键．7、如图，在△ABC中，∠ABC=45°,AD,BE分别为BC,AC边上的高，AD,BE相交于点F，连接CF，则下列结论：①BF=AC；②∠FCD=∠DAC；③CF⊥AB；④若BF=2EC，则△FDC周长等于AB的长．其中正确的有（）A．①②B．①③④C．①③D．②③④答案：B分析：证明△BDF≌△ADC，可判断①；求出∠FCD=45°，∠DAC＜45°，延长CF交AB于H，证明∠AHC=∠ABC+∠FCD=90°，可判断③；根据①可以得到E是AC的中点，然后可以推出EF是AC的垂直平分线，最后由线段垂直平分线的性质可判断④．解：∵△ABC中，AD，BE分别为B C、AC边上的高，∠ABC=45°，∴AD=BD，∠DAC和∠FBD都是∠ACD的余角，而∠ADB=∠ADC=90°，∴△BDF≌△ADC（ASA），∴BF=AC，FD=CD，故①正确，∵∠FDC=90°，∴∠DFC=∠FCD=45°，∵∠DAC=∠DBF＜∠ABC=45°，∴∠FCD≠∠DAC，故②错误；延长CF交AB于H，∵∠ABC=45°，∠FCD=45°，∴∠AHC=∠ABC+∠FCD=90°，∴CH⊥AB，即CF⊥AB，故③正确；∵BF=2EC，BF=AC，∴AC=2EC，∴AE=EC=1AC，2∵BE⊥AC，∴BE垂直平分AC，∴AF=CF，BA=BC，∴△FDC的周长=FD+FC+DC=FD+AF+DC=AD+DC=BD+DC=BC=AB，即△FDC的周长等于AB，故④正确，综上：①③④正确，故选B．小提示：本题考查了全等三角形的性质与判定，也考查了线段的垂直平分线的性质与判定，也利用了三角形的周长公式解题，综合性比较强，对学生的能力要求比较高．＜8、如图，在等边△ABC中，AB＝4cm，BD平分∠ABC，点E在BC的延长线上，且∠E=30∘，则CE的长是（）A．1cmB．2cmC．3cmD．4cm答案：B分析：根据等边三角形的性质得AC=AB=4，由等边三角形三线合一得到CD，由∠ACB=60°，∠E=30°，求出∠CDE，得出CD=CE，即可求解．∵△ABC是等边三角形，∴AC= AB=BC=4cm，∠ACB = 60°，∵BD平分∠ABC，∴AD=CD(三线合一)∴DC=12AC=12×4=2cm，∵∠E = 30°∴∠CDE=∠ACB-∠E=60°-30°=30°∴∠CDE=∠E所以CD=CE=2cm故选：B．小提示：本题考查的是等边三角形的性质、等腰三角形的判定，直角三角形的性质，直角三角形中30°角所对的直角边等于斜边的一半．9、如图，点P为∠AOB内一点，分别作点P关于OB、OA的对称点P1，P2，连接P1P2交OB于M，交OA于N，P1P2=15，则△PMN的周长为（）A．16B．15C．14D．13答案：B分析：根据轴对称的性质可得P1M＝PM，P2N＝PN，然后根据三角形的周长定义，求出△PMN的周长为P1P2，从而得解．解：∵点P关于OB、OA的对称点P1，P2，∴P1M=PM，P2N=PN，∴△PMN的周长=MN+PM+PN=MN+P1M+P2N=P1P2，∵P1P2=15∴△PMN的周长为15．故选：B．小提示：本题考查轴对称的性质，解题时注意：对应点所连的线段被对称轴垂直平分，对称轴上的任何一点到两个对应点之间的距离相等，对应的角、线段都相等．10、△ABC为等边三角形，点E为边AB的中点，点Q为边BC上一动点，以EQ为边作等边△EQF（点F在EQ 的右侧），连接AF、FC，点P在射线CB上，且满足PE=EQ，有以下四个结论①∠FQC＝∠QEB；②FQ＝FC；③PB+QC=AE；④当AF⊥AB时，BC＝4PB，其中正确的结论的个数是（）A．1个B．2个C．3个D．4个答案：C分析：取BC中点H，连接EH、FH，作EG⊥BC于G，根据三角形内角和定理和平角的定义得出∠FQC＋∠EQF＋∠EQB＝∠QEB＋∠EBQ＋∠EQB＝180°，进而可得∠FQC＝∠QEB，故①正确；根据点E为边AB的中点，点H为边BC的中点，可得AE＝EB＝BH＝HC，△EBH是等边三角形，然后求出PB＝HQ即可得出PB＋QC＝HC＝AE，故③正确；通过证明△PEH≌△FEH可得∠EHP＝∠EHF＝60°，求出∠EHF＝∠CHF，再证△EHF≌△CHF，求出FC ＝EF即可得出FQ＝FC，故②正确；当CQ＝HQ时，BC＝4PB，由AF⊥AB无法推出Q为HC中点，故④错误．解：取BC中点H，连接EH、FH，作EG⊥BC于G，∵△ABC为等边三角形，△EQF为等边三角形，∴∠EQF＝∠EBQ＝60°，∵∠FQC＋∠EQF＋∠EQB＝∠QEB＋∠EBQ＋∠EQB＝180°，∴∠FQC＝∠QEB，故①正确；∵EG⊥BC，PE=EQ，∴PG＝GQ，∵点E为边AB的中点，点H为边BC的中点，∠ABC＝60°，∴AE＝EB＝BH＝HC，∴△EBH是等边三角形，∵EG⊥BH，∴BG＝GH，∴PB＝HQ，∴PB＋QC＝HC＝AE，故③正确；∵EG⊥BC，PE=EQ，△EBH是等边三角形，∴∠BEG＝∠HEG，∠PEG＝∠QEG，∠BEH＝∠EHB＝60°，EH＝EB，∴∠PEB＝∠QEH，∵在等边三角形△EQF中，∠FEQ＝60°，EF＝EQ＝FQ，∴∠PEH＝∠FEH，PE＝FE，又∵EH＝EH，∴△PEH≌△FEH（SAS），∴∠EHP＝∠EHF＝60°，∴∠FHC＝60°，即∠EHF＝∠CHF，∵AE＝EB＝BH＝HC，EH＝EB，∴EH＝HC，又∵HF＝HF，∴△EHF≌△CHF（SAS），∴FC＝EF，∴FQ＝FC，故②正确；④∵BH＝CH，BG＝GH，BP＝HQ，∴当CQ＝HQ时，BC＝4PB，由AF⊥AB无法推出Q为HC中点，故④错误；综上，正确的有3个，故选：C．小提示：本题考查了等边三角形的判定和性质，等腰三角形的判定和性质，全等三角形的判定和性质等知识，作出合适的辅助线，构造出等边三角形和全等三角形是解题的关键．填空题11、如图，在Rt△ABC中，∠C=90°，∠A=30°，线段AB的垂直平分线分别交AC、AB于点D、E，连结BD．若CD=1，则AD的长为________．答案：2分析：根据线段垂直平分线的性质得到AD=BD，∠ABD=∠A=30°，求得∠CBD=30°，即可求出答案．解：∵∠C=90°，∴∠A+∠ABC=90°，∵线段AB的垂直平分线分别交AC、AB于点D、E，∴AD=BD，∴∠ABD=∠A=30°，∴∠CBD=30°，∵CD=1，∴AD=BD=2CD=2，所以答案是：2．小提示：此题考查线段垂直平分线的性质，直角三角形30度角的性质，熟记线段垂直平分线的性质是解题的关键．12、在“锐角、五角星、等边三角形、圆、正六边形”这五个图形中，是轴对称图形的有________个，按对称轴条数由多到少排列是_______________．答案： 5 圆、正六边形、五角星、等边三角形、锐角分析：根据轴对称图形的定义：如果一个平面图形沿一条直线折叠，直线两旁的部分能够完全重合，这个图形就叫轴对称图形，这条直线就叫做对称轴，进行求解即可．解：锐角时轴对称图形，对称轴为1条；五角星是轴对称图形，对称轴有5条；等边三角形是轴对称图形，对称轴有3条；圆是轴对称图形，对称轴有无数条；正六边形是轴对称图形，对称轴有6条，所以答案是：5；圆，正六边形，五角星，等边三角形，锐角．小提示：本题主要考查了轴对称图形，解题的关键在于能够熟练掌握相关知识进行求解．13、如图，在ΔABC中，AB=7cm，BC=5cm，AC的垂直平分线分别交AB，AC于点D，E，点F是DE上的任意一点，则ΔBCF周长的最小值是________cm．答案：12分析：当F点于D重合时，ΔBCF的周长最小，根据垂直平分线的性质，即可求出ΔBCF的周长．∵DE垂直平分AC，∴点C与A关于DE对称，∴当F点于D重合时，即A、D、B三点在一条直线上时，BF+CF=AB最小，（如图），∴ΔBCF的周长为：CΔBCF=BD+CD+BC，∵DE是垂直平分线，∴AD=CD，又∵AB=7cm，∴BD+AD=BD+CD=7cm，∴CΔBCF=7+5=12cm，所以答案是：12．小提示：本题考查最短路径问题以及线段垂直平分线的性质：垂直平分线上的点到线段两端的距离相等，熟练掌握最短路径的求解方法以及垂直平分线的性质是解题的关键．14、如图，图1是长方形纸带，将纸带沿EF折叠成图2，再沿BF折叠成图3，若图3中∠CFE=108°，则图1中的∠DEF的度数是______．答案：24°##24度分析：先根据平行线的性质，设∠DEF＝∠EFB＝a，图2中根据图形折叠的性质得出∠AEF的度数，再由平行线的性质得出∠GFC，图3中根据∠CFE＝∠GFC﹣∠EFG即可列方程求得a的值．∵AD∥BC，∴设∠DEF＝∠EFB＝a，图2中，∠GFC＝∠BGD＝∠AEG＝180°﹣2∠DEF＝180°﹣2a，图3中，∠CFE＝∠GFC﹣∠EFG＝180°﹣2a﹣a＝108°．解得a＝24°．即∠DEF＝24°，所以答案是：24°．小提示：本题考查图形的翻折变换以及平行线的性质，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．15、如图，在△ABC中，BC的垂直平分线分别交BC、AB于点E、F．若△AFC是等边三角形，则∠B=_________°．答案：30分析：根据垂直平分线的性质得到∠B=∠BCF，再利用等边三角形的性质得到∠AFC=60°，从而可得∠B.解：∵EF垂直平分BC，∴∠B=∠BCF，∵△ACF为等边三角形，∴∠AFC=60°，∴∠B=∠BCF=30°.所以答案是：30.小提示：本题考查了垂直平分线的性质，等边三角形的性质，外角的性质，解题的关键是利用垂直平分线的性质得到∠B=∠BCF.解答题16、如图：在正方形网格中有一个△ABC，按要求进行下列作图（只能借助于网格）：(1)画出△ABC中BC边上的高AD；(2)画出先将△ABC向左平移5格，再向下平移2格后的△A1B1C1；(3)画一个△BCP（要求各顶点在格点上，P不与A点重合），使其面积等于△ABC的面积．并回答，满足这样条件的点P共______个．答案：(1)见解析；(2)见解析；(3)见解析；2分析：（1）根据三角形高的定义求解可得；（2）根据平移的定义作出变换后的对应点，再顺次连接即可得；（3）过点A作平行于BC的直线，同样结合网格的特点在直线BC的另一侧也可以找出符合条件的格点P，共（1）解：如图：作BF⊥BC，再过A点作BF的平行线，交BC于点D，（2）解：如图：（3）解：如图符合条件的格点共有4个，小提示：本题用到的知识点为：三角形一边上的高为这边所对的顶点向这边所引的垂线段，对称的性质；图形的平移要归结为各顶点的平移，平行线间距离处处相等．17、如图，在△ABC中，AB=AC，∠B=30°，线段AB的垂直平分线MN交BC于D，求证：CD=2BD．答案：见解析分析：连接AD，首先根据垂直平分线的性质得到∠DAB=∠B=30°，然后根据AB=AC，求出∠B=∠C=30°，∠DAC=90°，最后根据30°角所对的直角边是斜边的一半即可证明出CD=2BD．证明：连接AD，∵直线MN是线段AB的垂直平分线，∴AD=BD，∴∠DAB=∠B，又∵∠B=30°，∴∠DAB=30°，又∵AB=AC，∠B=30°，∴∠B=∠C=30°，∠BAC=120°，∴∠DAC=90°，又∵∠C=30°，∴CD=2AD，又∵AD=BD，∴CD=2BD．小提示：此题考查了等腰三角形的性质，30°角直角三角形的性质，解题的关键是连接AD求出∠DAB=∠B=30°．18、如图，在△ABC中，BE是角平分线，AD⊥BE，垂足为D．求证：∠2=∠1+∠C．答案：见解析分析：延长AD交BC于点F，由BE是角平分线、AD⊥BE可知△ABF是等腰三角形且∠2＝∠AFB，根据∠AFB＝∠1＋∠C可得证．证明：如图，延长AD交BC于点F，∵BE是∠ABC的角平分线，AD⊥BE，∴AB=FB，∴∠2=∠AFB，∵∠AFB=∠1+∠C，∴∠2=∠1+∠C．小提示：本题主要考查等腰三角形的判定与性质，解题的关键是掌握等腰三角形三线合一的性质．。

数学八（上）《线段、角的轴对称性》练习1.在一张薄纸上任意化一个三角形ABC,用折纸的方法分别折出边AB和AC的垂直平分线了l1和l2，l2的交点为0.点O在边BC的垂直平分线上吗为什么（第1题答案）答案：点O在边BC的垂直平分线上，因为点O在AB、AC的垂直平分线上，所以OA=OB,OA=OC,理由是：线段垂直平分线上的点到线段两端的距离相等。

由此得到OB=OC，所以点O在BC的垂直平分线上。

理由是：到线段两端距离相等的点，在线段的垂直平分线上。

2.利用网络线画图：（1）在图①中，画线段PQ的垂直平分线；（2）在图②中，找一点O，使OA=OB=OC。

答案：2. （1）（2）○1（第2题答案）○2借助网络和全等三角形的知识，图○1中关键是找出M和点N ;图○2中要找的点O在垂直平分BC的网络线上。

3.任意画一个钝角三角形ABC（∠A＞90°）（1）用直尺和圆规分别作两边AB和AC的垂直平分线l1和l2（2）l1、l2的交点O到点B、C的距离是否相等答案：（1）（第3题答案）（2）OB=OC.4.（1）在一张薄纸上画△ABC及其两个外角（如图），用折纸的方法分别折出∠BAD和∠ABE的平分线，设两条折痕的交点为O;（2）用直尺和圆规∠C的平分线CF，如果你折纸和作图都十分准确，点O 应该在射线CF上，这是为什么(第4题) (第4题答案)答案：（1）略（2）因为点O分别在∠BAD和∠ABE的平分线上，所以点O到AD 的距离等于点O到AB的距离。

点O到BE 的距离等于点O到AB的距离，于是可得点O到AD、BE的距离相等、所以点O 在∠C的平分线上。

5.利用网格想作图：（1）在BC上找一点P，使点P到AB和AC的距离相等;(2) 在射线AP上找一点Q，使QB = QC .（第5题）答案：图略。

（1）只有任意找一个A为顶点的格点正方形，过点A的对角线或其延长线与BC的交点就是点P;(2) 在以A为一个顶点、边长为5的正方形中，与点A 相对的顶点就是Q。

2.4 线段、角的轴对称性一．选择题1．如图，点P 是∠AOB 平分线OC 上一点，PD ⊥OB ，垂足为D ，若PD=2，则点P 到边OA 的距离是（ ）A ．1B ．2C ．D ．4第1题 第2题 第3题2．如图，在Rt △ABC 中，∠C=90°，以顶点A 为圆心，适当长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于MN 的长为半径画弧，两弧交于点P ，作射线AP 交边BC 于点D ，若CD=4，AB=15，则△ABD 的面积是（ ）A ．15B ．30C ．45D ．603．如图，△ABC 的三边AB ，BC ，CA 长分别是20，30，40，其三条角平分线将△ABC 分为三个三角形，则S △ABO ：S △BCO ：S △CAO 等于（ ）A ．1：1：1B ．1：2：3C ．2：3：4D ．3：4：5 4．如图，在CD 上求一点P ，使它到OA ，OB 的距离相等，则P 点是（ ）A ．线段CD 的中点B ．OA 与OB 的中垂线的交点C ．OA 与CD 的中垂线的交点 D ．CD 与∠AOB 的平分线的交点第4题 第5题 第6题5．如图，OP 是∠AOB 的平分线，点P 到OA 的距离为3，点N 是OB 上的任意一点，则线段PN 的取值范围为（ ）A ．PN ＜3B ．PN ＞3C ．PN ≥3D ．PN ≤36．如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC=7，DE=2，AB=4，则AC长是（）A．3 B．4 C．6 D．57．如图，已知点P是∠AOB角平分线上的一点，∠AOB=60°，PD⊥OA，M是OP 的中点，DM=4cm，如果点C是OB上一个动点，则PC的最小值为（）A．2 B．2C．4 D．4第7题第8题第9题8．如图所示，直线l1，l2，l3表示三条相交的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（）A．1处B．2处C．3处D．4处9．如图，∠AOB和一条定长线段a，在∠AOB内找一点P，使P到OA，OB的距离都等于a，作法如下：（1）作OB的垂线段NH，使NH=a，H为垂足．（2）过N作NM∥OB．（3）作∠AOB的平分线OP，与NM交于P．（4）点P即为所求．其中（3）的依据是（）A．平行线之间的距离处处相等B．到角的两边距离相等的点在角的平分线上C．角的平分线上的点到角的两边的距离相等D．到线段的两个端点距离相等的点在线段的垂直平分线上二．填空题10．如图，已知在△ABC中，DE是BC的垂直平分线，垂足为E，交AC于点D，若AB=6，AC=9，则△ABD的周长是．11．如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC=7，DE=2，AB=4，则AC长是．第10题第11题12．如图，已知射线OC上的任意一点到∠AOB的两边的距离都相等，点D、E、F分别为边OC、OA、OB上，如果要想证得OE=OF，只需要添加以下四个条件中的某一个即可，请写出所有可能的条件的序号．①∠ODE=∠ODF；②∠OED=∠OFD；③ED=FD；④EF⊥OC．第12题第13题13．如图，已知：△ABC中，∠C=90°，AC=40，BD平分∠ABC交AC于D，AD：DC=5：3，则D点到AB的距离是．三．解答题14．如图，OM平分∠POQ，MA⊥OP，MB⊥OQ，A、B为垂足，AB交OM于点N．求证：∠OAB=∠OBA．15．如图，在Rt△ABC中，∠ABC=90°，CD平分∠ACB交AB于点D，DE⊥AC于点E，BF∥DE交CD于点F．求证：DE=BF．16．如图，在△ABC中，BC的垂直平分线交BC于点D，交AB延长线于点E，连接CE．求证：∠BCE=∠A+∠ACB．17．如图，在△ABC中，∠A=60°，点D是BC边的中点，DE⊥BC，∠ABC的角平分线BF交DE于△ABC内一点P，连接PC．（1）若∠ACP=24°，求∠ABP的度数；（2）若∠ACP=m°，∠ABP=n°，请直接写出m，n满足的关系式：．18．如图，在△ABC中，AC边的垂直平分线DM交AC于D，BC边的垂直平分线EN交BC于E，DM与EN相交于点F（1）若△CMN的周长为20cm，求AB的长；（2）若∠MFN=70°，求∠MCN的度数．19．如图，在△ABC中，AB边的垂直平分线l1交BC于点D，AC边的垂直平分线l2交BC于点E，l1与l2相交于点O，连结0B，OC，若△ADE的周长为6cm，△OBC的周长为16cm．（1）求线段BC的长；（2）连结OA，求线段OA的长；（3）若∠BAC=120°，求∠DAE的度数．20．如图，AD为△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF 交AD于点G．（1）求证：AD垂直平分EF；（2）若∠BAC=60°，猜测DG与AG间有何数量关系？请说明理由．参考答案与试题解析一．选择题1．（2017•台州）如图，点P是∠AOB平分线OC上一点，PD⊥OB，垂足为D，若PD=2，则点P到边OA的距离是（）A．1 B．2 C．D．4【分析】作PE⊥OA于E，根据角平分线的性质解答．【解答】解：作PE⊥OA于E，∵点P是∠AOB平分线OC上一点，PD⊥OB，PE⊥OA，∴PE=PD=2，故选：B．【点评】本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．2．（2017•枣庄）如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=4，AB=15，则△ABD的面积是（）A．15 B．30 C．45 D．60【分析】判断出AP 是∠BAC 的平分线，过点D 作DE ⊥AB 于E ，根据角平分线上的点到角的两边距离相等可得DE=CD ，然后根据三角形的面积公式列式计算即可得解．【解答】解：由题意得AP 是∠BAC 的平分线，过点D 作DE ⊥AB 于E ， 又∵∠C=90°，∴DE=CD ，∴△ABD 的面积=AB•DE=×15×4=30．故选B ．【点评】本题考查了角平分线上的点到角的两边距离相等的性质以及角平分线的画法，熟记性质是解题的关键．3．如图，△ABC 的三边AB ，BC ，CA 长分别是20，30，40，其三条角平分线将△ABC 分为三个三角形，则S △ABO ：S △BCO ：S △CAO 等于（ ）A ．1：1：1B ．1：2：3C ．2：3：4D ．3：4：5【分析】利用角平分线上的一点到角两边的距离相等的性质，可知三个三角形高相等，底分别是20，30，40，所以面积之比就是2：3：4．【解答】解：利用同高不同底的三角形的面积之比就是底之比可知选C ． 故选C ．【点评】本题主要考查了角平分线上的一点到两边的距离相等的性质及三角形的面积公式．做题时应用了三个三角形的高时相等的，这点式非常重要的．4．如图，在CD 上求一点P ，使它到OA ，OB 的距离相等，则P 点是（ ）A．线段CD的中点B．OA与OB的中垂线的交点C．OA与CD的中垂线的交点D．CD与∠AOB的平分线的交点【分析】利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交点．【解答】解：利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交于点P．故选D．【点评】本题主要考查了角平分线上的一点到两边的距离相等的性质．做题时注意题目要求要满足两个条件①到角两边距离相等，②点在CD上，要同时满足．5．如图，OP是∠AOB的平分线，点P到OA的距离为3，点N是OB上的任意一点，则线段PN的取值范围为（）A．PN＜3 B．PN＞3 C．PN≥3 D．PN≤3【分析】作PM⊥OB于M，根据角平分线的性质得到PM=PE，得到答案．【解答】解：作PM⊥OB于M，∵OP是∠AOB的平分线，PE⊥OA，PM⊥OB，∴PM=PE=3，∴PN≥3，故选：C．【点评】本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．6．如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC=7，DE=2，AB=4，则AC长是（）A．3 B．4 C．6 D．5【分析】作DH⊥AC于H，如图，利用角平分线的性质得DH=DE=2，根据三角形的面积公式得×2×AC+×2×4=7，于是可求出AC的值．【解答】解：作DH⊥AC于H，如图，∵AD是△ABC中∠BAC的角平分线，DE⊥AB，DH⊥AC，∴DH=DE=2，∵S△ABC =S△ADC+S△ABD，∴×2×AC+×2×4=7，∴AC=3．故选A．【点评】本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等．这里的距离是指点到角的两边垂线段的长．7．如图，已知点P是∠AOB角平分线上的一点，∠AOB=60°，PD⊥OA，M是OP 的中点，DM=4cm，如果点C是OB上一个动点，则PC的最小值为（）A．2 B．2 C．4 D．4【分析】根据角平分线的定义可得∠AOP=AOB=30°，再根据直角三角形的性质求得PD=OP=4，然后根据角平分线的性质和垂线段最短得到结果．【解答】解：∵P是∠AOB角平分线上的一点，∠AOB=60°，∴∠AOP=AOB=30°，∵PD⊥OA，M是OP的中点，DM=4cm，∴OP=2DM=8，∴PD=OP=4，∵点C是OB上一个动点，∴PC的最小值为P到OB距离，∴PC的最小值=PD=4．故选C．【点评】本题考查了角平分线上的点到角的两边距离相等的性质，直角三角形的性质，熟记性质并作出辅助线构造成直角三角形是解题的关键．8．如图所示，直线l1，l2，l3表示三条相交的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（）A．1处 B．2处 C．3处 D．4处【分析】根据到三条相互交叉的公路距离相等的地点应是三条角平分线的交点．把三条公路的中心部位看作三角形，那么这个三角形两个内角平分线的交点以及三个外角两两平分线的交点都满足要求．【解答】解：满足条件的有：（1）三角形两个内角平分线的交点，共一处；（2）三个外角平分线两两相交的交点，共三处．故选：D．【点评】本题考查了角平分线的性质；这是一道生活联系实际的问题，解答此类题目时最直接的判断就是三角形的角平分线，很容易漏掉外角平分线，解答时一定要注意，不要漏解．9．如图，∠AOB和一条定长线段a，在∠AOB内找一点P，使P到OA，OB的距离都等于a，作法如下：（1）作OB的垂线段NH，使NH=a，H为垂足．（2）过N作NM∥OB．（3）作∠AOB的平分线OP，与NM交于P．（4）点P即为所求．其中（3）的依据是（）A．平行线之间的距离处处相等B．到角的两边距离相等的点在角的平分线上C．角的平分线上的点到角的两边的距离相等D．到线段的两个端点距离相等的点在线段的垂直平分线上【分析】题目要求满足两个条件，其一是到角OA，OB的距离相等，作角平分线，根据到角的两边距离相等的点在角平分线上，可得答案．【解答】解：根据角平分线的性质，（3）的依据是到角的两边的距离相等的点在角平分线上，故选B．【点评】本题主要考查到角的两边距离相等的点在角的平分线上的知识；注意本题容易出现选C的错误．二．填空题10．（2017•常州）如图，已知在△ABC中，DE是BC的垂直平分线，垂足为E，交AC于点D，若AB=6，AC=9，则△ABD的周长是15．【分析】根据线段的垂直平分线的性质得到DB=DC，根据三角形的周长公式计算即可．【解答】解：∵DE是BC的垂直平分线，∴DB=DC，∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=15，故答案为：15．【点评】本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．11．如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC=7，DE=2，AB=4，则AC长是3．【分析】根据角平分线上的点到角的两边距离相等可得DE=DF，再根据三角形的面积公式列式计算即可得解．【解答】解：∵AD是△ABC中∠BAC的角平分线，DE⊥AB，DF⊥AC，∴DE=DF，=×4×2+AC•2=7，∴S△ABC解得AC=3．故答案为：3．【点评】本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质是解题的关键．12．如图，已知射线OC上的任意一点到∠AOB的两边的距离都相等，点D、E、F分别为边OC、OA、OB上，如果要想证得OE=OF，只需要添加以下四个条件中的某一个即可，请写出所有可能的条件的序号①②④．①∠ODE=∠ODF；②∠OED=∠OFD；③ED=FD；④EF⊥OC．【分析】由射线OC上的任意一点到∠AOB的两边的距离都相等，根据角平分线的判定定理可知OC平分∠AOB．要得到OE=OF，就要让△ODE≌△ODF，①②④都行，只有③ED=FD不行，因为证明三角形全等没有边边角定理．【解答】解：∵射线OC上的任意一点到∠AOB的两边的距离都相等，∴OC平分∠AOB．①若①∠ODE=∠ODF，根据ASA定理可求出△ODE≌△ODF，由三角形全等的性质可知OE=OF．正确；②若∠OED=∠OFD，根据AAS定理可得△ODE≌△ODF，由三角形全等的性质可知OE=OF．正确；③若ED=FD条件不能得出．错误；④若EF⊥OC，根据ASA定理可求出△OGE≌△OGF，由三角形全等的性质可知OE=OF．正确．故答案为①②④．【点评】本题主要考查了角平分线的判定，三角形全等的判定与性质；由求线段相等转化为添加条件使三角形全等是正确解答本题的关键．13．如图，已知：△ABC中，∠C=90°，AC=40，BD平分∠ABC交AC于D，AD：DC=5：3，则D点到AB的距离是15．【分析】先求出CD的长，再根据角平分线的性质即可得出结论．【解答】解：∵AC=40，AD：DC=5：3，∴CD=40×=15．∵BD平分∠BAC交AC于D，∴D点到AB的距离是15．故答案为：15．【点评】本题考查的是角平分线的性质，熟知角的平分线上的点到角的两边的距离相等是解答此题的关键．三．解答题14．如图，OM平分∠POQ，MA⊥OP，MB⊥OQ，A、B为垂足，AB交OM于点N．求证：∠OAB=∠OBA．【分析】根据角平分线上的点到角的两边的距离相等可得AM=BM，然后利用“HL”证明Rt△AOM和Rt△BOM全等，根据全等三角形对应边相等可得OA=OB，再根据等边对等角的性质即可得证．【解答】证明：∵OM平分∠POQ，MA⊥OP，MB⊥OQ，∴AM=BM，在Rt△AOM和Rt△BOM中，，∴Rt△AOM≌Rt△BOM（HL），∴OA=OB，∴∠OAB=∠OBA．【点评】本题考查了角平分线上的点到角的两边的距离相等的性质，全等三角形的判定与性质，等边对等角的性质，熟记性质是解题的关键．15．如图，在Rt△ABC中，∠ABC=90°，CD平分∠ACB交AB于点D，DE⊥AC于点E，BF∥DE交CD于点F．求证：DE=BF．【分析】根据角平分线的定义得到∠1=∠2，根据角平分线的性质得到DE=BD，∠3=∠4，由平行线的性质得到3=∠5，于是得到结论．【解答】证明：∵CD平分∠ACB，∴∠1=∠2，∵DE⊥AC，∠ABC=90°∴DE=BD，∠3=∠4，∵BF∥DE，∴∠4=∠5，∴∠3=∠5，∴BD=BF，∴DE=BF．【点评】本题考查了角平分线的性质，平行线的性质，等腰三角形的判定和性质，熟练掌握角平分线的性质是解题的关键．16．如图，在△ABC中，BC的垂直平分线交BC于点D，交AB延长线于点E，连接CE．求证：∠BCE=∠A+∠ACB．【分析】根据线段垂直平分线的想知道的CE=BE，根据等腰三角形的性质得到∠ECB=∠EBC，根据三角形的外角的性质即可得到结论．【解答】证明：∵BC的垂直平分线交BC于点D，交AB延长线于点E，∴CE=BE，∴∠ECB=∠EBC，∵∠EBC=∠A+∠ACB，∴∠BCE=∠A+∠ACB．【点评】本题考查了线段垂直平分线的性质，等腰三角形的性质，三角形的外角的性质，熟练掌握线段垂直平分线的性质是解题的关键．17．如图，在△ABC中，∠A=60°，点D是BC边的中点，DE⊥BC，∠ABC的角平分线BF交DE于△ABC内一点P，连接PC．（1）若∠ACP=24°，求∠ABP的度数；（2）若∠ACP=m°，∠ABP=n°，请直接写出m，n满足的关系式：m+3n=120．【分析】（1）根据线段垂直平分线的性质，可得∠PBC=∠PCB，根据角平分线的定义，可得∠PBC=∠PCB=∠ABP，最后根据三角形内角和定理，即可得到∠ABP 的度数；（2）运用（1）中的方法，即可得出m，n满足的关系式．【解答】解：（1）∵点D是BC边的中点，DE⊥BC，∴PB=PC，∴∠PBC=∠PCB，∵BP平分∠ABC，∴∠PBC=∠ABP，∴∠PBC=∠PCB=∠ABP，∵∠A=60°，∠ACP=24°，∴∠PBC+∠PCB+∠ABP=120°﹣24°，∴3∠ABP=120°﹣24°，∴∠ABP=32°；（2）∵点D是BC边的中点，DE⊥BC，∴PB=PC，∴∠PBC=∠PCB，∵BP平分∠ABC，∴∠PBC=∠ABP，∴∠PBC=∠PCB=∠ABP=n°，∵∠A=60°，∠ACP=m°，∴∠PBC+∠PCB+∠ABP=120°﹣m°，∴3∠ABP=120°﹣m°，∴3n°+m°=120°，故答案为：m+3n=120．【点评】本题主要考查了三角形内角和定理以及线段垂直平分线的性质的运用，解题时注意：线段垂直平分线上任意一点，到线段两端点的距离相等；三角形内角和等于180°．18．如图，在△ABC中，AC边的垂直平分线DM交AC于D，BC边的垂直平分线EN交BC于E，DM与EN相交于点F（1）若△CMN的周长为20cm，求AB的长；（2）若∠MFN=70°，求∠MCN的度数．【分析】（1）根据线段的垂直平分线的性质得到MA=MC，NB=NC，根据三角形的周长公式计算即可；（2）根据四边形内角和定理和等腰三角形的性质求出∠A+∠B=70°，由∠MCA=∠A，∠NCB=∠B，计算即可．【解答】解：（1）∵DM是AC边的垂直平分线，∴MA=MC，∵EN是BC边的垂直平分线，∴NB=NC，AB=AM+MN+NB=MC+MN+NC=△CMN的周长=20cm；（2）∵MD⊥AC，NE⊥BC，∴∠ACB=180°﹣∠MFN=110°，∴∠A+∠B=70°，∵MA=MC，NB=NC，∴∠MCA=∠A，∠NCB=∠B，∴∠MCN=40°．【点评】本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键，注意三角形内角和定理的应用．19．如图，在△ABC中，AB边的垂直平分线l1交BC于点D，AC边的垂直平分线l2交BC于点E，l1与l2相交于点O，连结0B，OC，若△ADE的周长为6cm，△OBC的周长为16cm．（1）求线段BC的长；（2）连结OA，求线段OA的长；（3）若∠BAC=120°，求∠DAE的度数．【分析】（1）根据线段垂直平分线的性质得到DA=DB，EA=EC，根据三角形的周长公式计算即可；（2）根据线段垂直平分线的性质和三角形的周长公式计算即可；（3）根据线段垂直平分线的性质和等腰三角形的性质进行计算．【解答】解：（1）∵l1是AB边的垂直平分线，∴DA=DB，∵l2是AC边的垂直平分线，∴EA=EC，BC=BD+DE+EC=DA+DE+EA=6cm；（2）∵l1是AB边的垂直平分线，∴OA=OB，∵l2是AC边的垂直平分线，∴OA=OC，∵OB+OC+BC=16cm，∴OA=0B=OC=5cm；（3）∵∠BAC=120°，∴∠ABC+∠ACB=60°，∵DA=DB，EA=EC，∴∠BAD=∠ABC，∠EAC=∠ACB，∴∠DAE=∠BAC﹣∠BAD﹣∠EAC=60°．【点评】本题考查的是线段的垂直平分线的性质等几何知识．线段的垂直平分线上的点到线段的两个端点的距离相等．20．如图，AD为△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF 交AD于点G．（1）求证：AD垂直平分EF；（2）若∠BAC=60°，猜测DG与AG间有何数量关系？请说明理由．【分析】（1）由AD为△ABC的角平分线，得到DE=DF，推出∠AEF和∠AFE相等，得到AE=AF，即可推出结论；（2）由已知推出∠EAD=30°，得到AD=2DE，在△DEG 中，由∠DEG=30°推出DE=2DG，即可推出结论．【解答】（1）证明：∵AD为△ABC的角平分线，DE⊥AB，DF⊥AC，∴DE=DF，∠AED=∠AFD=90°，∴∠DEF=∠DFE，∴∠AEF=∠AFE，∴AE=AF∴点A、D都在EF的垂直平分线上，∴AD垂直平分EF．（2）答：AG=3DG．理由：∵∠BAC=60°，AD平分∠BAC，∴∠EAD=30°，∴AD=2DE，∠EDA=60°，∵AD⊥EF，∴∠EGD=90°，∴∠DEG=30°∴DE=2DG，∴AD=4DG，∴AG=3DG．【点评】本题主要考查了角平分线的性质，线段垂直平分线的性质，含30°角的直角三角形的性质等知识点，解此题的关键是（1）证AE=AF和DE=DF；（2）证AD=2DE和DE=2DG．题目比较典型，综合性强．21。

初中数学试卷马鸣风萧萧2.4线段、角的轴对称性【基础训练】1．线段是轴对称图形，它的对称轴是_______；角是轴对称图形，它的对称轴是_______．2．角平分线上的任意一点到这个角的两边的_______相等；线段垂直平分线上的点到_______的距离相等；线段的垂直平分线可以看作是到_______的所有点的集合；角平分线可以看作是到_______的所有点的集合．3．射线OC平分∠AOB，点P在OC上，且PM⊥OA于点M，PN⊥OB于点N，且PM ＝2 cm，则PN＝________cm．4．如图，在△ABC中，DE是BC的垂直平分线．(1)若BE＝10 cm，则EC＝________cm；(2)若AB＋AC＝8 cm，则△ACE的周长是_______．5．如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D．(1)若BC＝8，BD＝5，则点D到AB的距离是_______；(2)若BD：DC＝3：2，点D到AB的距离为6，则BC的长是_______．6．已知△ABC，在△ABC内求作一点P，使它到△ABC三个顶点的距离相等．7．如图，点P是∠BAC的角平分线AD上的一点，PE⊥AC于点E．已知PE－3，则点．P 到AB的距离是( )．A．3 B．4 C．5 D．68．如图，在Rt△ABC中，∠B＝90°，ED是AC的垂直平分线，交AC于点D，交BC 于点E．已知∠BAE＝10°，则∠C的度数为()．A．30° B 40°C．50°D．60°9．如图，在△ABC中，边BC上的垂直平分线DE交边BC于点D，交边AB于点E．若△EDC的周长为24，△ABC与四边形AEDC的周长之差为12，则线段DE的长为_______．10．如图，在△ABC中，BC＝5 cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD ∥AB，PE∥AC，则△PDE的周长是_______cm．11．已知∠AOB和C、D两点，求作点P，使PC＝PD，且点P到∠AOB的两边OA、OB 的距离相等．【提优拔尖】12．如图，某市有一块由三条马路围成的三角形绿地，现准备在其中建一小亭供人们小憩，要求使小亭中心到三条马路的距离相等，试确定小亭的中心位置．13．如图，斜折一页书的一角，使点A落在同一页书内的点A'处，DE为折痕，作DF平分∠A'DB，试猜想∠FDE的度数，并说明理由．14．如图，在四边形ABCD中，AC垂直平分BD于点O．(1)图中有多少对全等三角形？请把它们都写出来；(2)任选(1)中的一对全等三角形加以证明．15．如图所示，在Rt△ABC中，∠ACB＝90°，∠B＝30°，ED是BC的垂直平分线，请写出图中两条相等的线段是_______．16．在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，若CD＝4，则点D到斜边AB的距离为_______．17．如图，△ABC的三边AB、BC、CA长分别为40，50，60，其三条角平分线交于点O，则S△ABO：S△BCO：S△CAO＝_______．18．如图，在四边形ABCD中，AD∥BC，对角线AC的中点为O，过点O作AC的垂直平分线分别与AD、BC相交于点E、F，连接AF．求证：AE＝AF．19．如图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个钝角为120°的菱形，剪口与第二次折痕所成角的度数应为（）A．15°或30°B．30°或45°C．45°或60°D．30°或60°20．如图，将长方形纸片ABCD 折叠，使边DC 落在对角线AC 上，折痕为CE ，且D 点落在对角线D ′处．若AB =3，AD =4，则ED 的长为（ ）A ．23B ．3C ．1D ．34 参考答案1．线段的垂直平分线或线段本身所在的直线 角的平分线2．距离 线段两端点 线段两端点距离相等 角两边距离相等3．2 4．(1)10 (2)8 cm5．(1)3 (2)156．P 是△ABC 任意两边垂直平分线的交点7．A 8．B9．6 10．511．点P 是CD 的垂直平分线与∠AOB 的角平分线的交点，图略．12．围成的图形正好是三角形，三角形角平分线的交点即为小亭的中心位置． 13．90°．14．(1)3对，△ABO ≌△ADO ，△BOC ≌△DOC ，△ABC ≌△ADC ．(2)略15．BD ＝CD(答案不唯一)16．4 17．4：5：618．略19．D20．A。