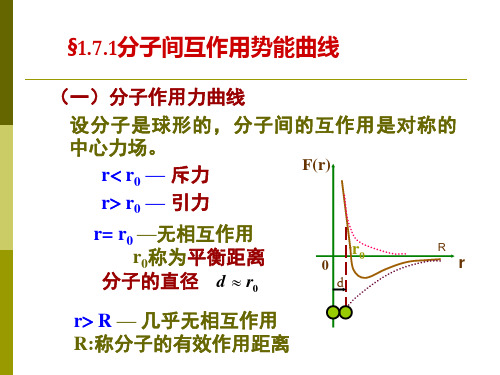
§1.7.1 分子间互作用势能曲线
- 格式:ppt
- 大小:125.50 KB
- 文档页数:6

分子间的相互作用势能与分子力罗兴垅【摘要】引入相对距离R、相对势能U与相对力F,导出了米势的相对势能U(R)及其相应的相对力F(R)与参数n、m的关系,并精确地绘制了伦纳德-琼斯势的相对势能U(R)曲线及其相应的相对力F(R)曲线和平衡位置附近的近似相对势能U(X)曲线、近似相对力F(X)曲线.%The paper introduces the relative distance,relative potential energy and relative power,derives the relative potential energy of Mie potential and its corresponding relative force and the relationships of parameter n and m,and accurately draws the relative potential energy curve of Leonard-Jones potential and its corresponding relative force curve and near the equilibrium position the approximate relative potential energy curve and the approximate relative force curve.【期刊名称】《赣南师范学院学报》【年(卷),期】2012(033)006【总页数】6页(P57-62)【关键词】米势;雷纳德—琼斯势;相对距离;相对势能;相对力【作者】罗兴垅【作者单位】赣南师范学院物理与电子信息学院,江西赣州341000【正文语种】中文【中图分类】O552物质由分子(或原子)组成,分子热运动和分子间的相互作用是决定物质各种热学性质的基本因素.分子间相互作用的关系很复杂,无法由实验直接测定,从理论(即使是量子理论)上也不容易得到一般性的解决,很难用简单的数学公式表示出来,通常采取的办法是在实验基础上采用简化模型来处理问题[1].一种常用的模型是假设分子间的相互作用具有球对称性,1907年米(Mie)指出,分子或原子间相互作用势为其中α>0,β>0,n>m >0,它们是通过实验确定的常数.式中第一项为排斥势,第二项为吸引势,且排斥势作用半径比吸引势作用半径小,式(1)简称为米势[2]. 在多数情况下,取m=6,n为9~12之间的整数,而以n=12为最佳[3].1924年,伦纳德-琼斯(Lennard-Jones)又提出了半经验公式式中u0是在平衡位置(r=r0)时的势能的绝对值.式(2)简称为伦纳德-琼斯势[4]. 由于米势、伦纳德-琼斯势中均有一对参数(两种表式分别为α、β或u0、r0)是待定的,与物质有关,对于米势还需选定n、m的值.因此,热学、热力学与统计物理学和固体物理学教材[1-9]一般仅绘制定性的分子势能曲线与分子力曲线.本文探讨米势的相对势能U及其相应的相对力F与参数n、m的关系,并以雷纳德—琼斯势为例,精确地绘制分子势能曲线与力曲线.1 米势1.1 米势由式(1),可得两分子间的相互作用力在平衡位置r0处,分子所受的力为零.令f(r0)=0,可解得式(4)代入式(1)得在平衡位置r0处,势能为u(r0),由上式有代入式(6)得由上式可知,米势由四个参数(u0、r0、n、m)确定.若给定某种分子的四个参数(u0、r0、n、m)值,则可绘制该种分子的势能曲线.当时,u(σ)=0,排斥势与吸引势的绝对值相等,且等于根据式(9)、式(10),可将式(8)改写成如下形式u(r)对r的一阶、二阶导数分别为由式(12)、(13)可知,在平衡位置r0处,势能有极小值u(r0)=-u0,势能曲线拐点位于由上述讨论可知米势的势能曲线特征为:(Ⅰ)当r→0时,u(r)→ +∞;当r→ +∞ 时,u(r)→0;在平衡位置r0(>σ)处,势能有极小值u(r0)=-u0.(Ⅱ)当0<r≤σ时,u(r)≥0;当σ <r<+∞ 时,u(r)<0.(Ⅲ)当0<r≤r0时,即势能随r的增大而减小;当r0<r<+∞ 时,即势能随r的增大而增大.(Ⅳ)势能曲线拐点位于δ(>r0)处,当0<r<δ时,曲线是凹的;当δ<r<+∞ 时,曲线是凸的.1.2 米势的相对势能令相对距离R=r/r0,相对势能U(R)=u(R)/u0,则式(8)变为上式表示米势的相对势能仅由二个参数(n、m)确定,与参数(r0、u0)无关.只要给定参数n、m的值,就可以绘制一类分子的相对势能曲线.1.3 米势的近似相对势能在讨论固体、液体中分子的热振动以及固体的热膨胀时,需要知道分子在平衡位置附近的势能曲线形状.为此,将米势u(r)在平衡位置r=r0处(即令r=r0+x)展开成泰勒级数式(8)对r的零阶、一阶、二阶与三阶导数在平衡位置r=r0处的值分别为代入米势u(r)的展开式,并保留到第四项,得上式为米势u(r)的近似式,其成立条件为x≪r0.若令相对距离X=x/r0,相对势能U(X)=u(x)/u0,则式(17)可改写为上式为米势u(r)的近似式,其成立条件为X≪1.若保留到第二项,则势能曲线为抛物线,分子应在平衡位置附近作简谐振动;若保留到第三项,则势能曲线不是抛物线,势能曲线在平衡位置附近不再对称,分子将在平衡位置附近作非简谐振动.1.4 米势的分子力式(4)代入式(3)得令 f0斥=mαr-(m+1)0 ,并由式(7)可得它是平衡位置r0处分子受到的斥力.于是,与米势相应的分子间的相互作用力为当r=r0时,f(r0)=0,排斥力与吸引力的大小相等.由(13)式可知,势能曲线拐点对应于力曲线的“极小值”令,可得力曲线拐点由上述讨论可知米势的力曲线特征为:(Ⅰ)当r→0时,f(r)→ +∞;当时r→ +∞,f(r)→0;在r=δ(对应于势能曲线拐点)处,f(r)有极小值.(Ⅱ)当0<r≤r0时,f(r)≥0;当r0<r<+∞ 时,f(r)<0.(Ⅲ)当0 <r≤ δ时,即f(r)随r的增大而减小;当δ<r<+∞ 时,即f(r)随r的增大而增大.(Ⅳ)力曲线拐点位于λ(>δ)处,当0<r<λ时,曲线是凹的;当λ<r<+∞ 时,曲线是凸的.1.5 米势的相对分子力令相对距离R=r/r0,相对力F(R)=f(r)/f0斥,则式(20)变为上式表示米势的相对力仅由二个参数(n、m)确定,与参数(r0、u0)无关.只要给定参数n、m的值,就可以绘制一类分子的相对力曲线.1.6 米势的近似相对分子力由式(17),可得米势的近似分子力为令相对距离X=x/r0,相对分子力F(X)=f(x)/f0斥,则式(24)可改写为(24)式与(25)式的成立条件均为X≪1.2 伦纳德—琼斯势2.1 伦纳德—琼斯势当米势中的m=6、n=12时,米势即为伦纳德-琼斯势令式(8)中的m=6、n=12,上式变为式(2)的形式令式(10)、式(11)中的m=6、n=12,则u斥(σ)=4u0,伦纳德-琼斯势可写成如下形式2.2 伦纳德—琼斯势的相对势能曲线令式(15)中的m=6、n=12,可得伦纳德-琼斯势的相对势能为根据上式,使用数学软件Matlab绘制雷纳德-琼斯势的相对势能曲线以及排斥势、吸引势的相对势能曲线,如图1所示.相对势能曲线是不对称的,平衡位置(R=1)的左边较陡,右边较平坦,势能曲线拐点位于R=1.108 7 处.图1 实线为雷纳德-琼斯势的相对势能曲线(右图中的上、下虚线分别为排斥势、吸引势的相对势能曲线)2.3 伦纳德—琼斯势的相对分子力曲线令式(20)中的m=6、n=12,可得伦纳德-琼斯势的分子力为式中f0斥=12u0/r0是平衡位置r0处分子受到的斥力.令式(23)中的m=6、n=12,可得伦纳德-琼斯势的相对分子力为根据上式,使用数学软件Matlab绘制雷纳德-琼斯势的相对力曲线以及排斥力、吸引力的相对力曲线,如图2所示.相对力曲线也是不对称的,平衡位置(R=1)的左边较陡,右边较平坦,力曲线拐点位于R=1.217 1 处.图2 实线为雷纳德-琼斯势的相对力曲线(右图中的上、下虚线分别为排斥力、吸引力的相对力曲线)表1 部分气体的参数值气体 He H2 Ne Ar Kr N2 O2 CO2 6 0.448 6 r0/nm0.295 2 0.322 2 0.312 1 0.382 2 0.404 1 0.415 1 0.388 4 0.503 6 u0/10 -20J 0.008 321 0.040 30 0.048 16 0.165 3 0.236 0 0.131 2 0.162 8 0.260 8 δ/nm 0.327 3 0.357 2 0.346 0 0.423 8 0.448 0 0.460 2 0.430 6 0.558 3 f(δ σ/nm 0.263 0.287 0.278 0.340 5 0.360 0.369 8 0.34 503 1 0.621 6)/10 -10N 0.007 586 0.033 66 0.041 54 0.116 4 0.157 2 0.085 04 0.112 8 0.139 4 f0斥 /10 -10N 0.033 82 0.150 1 0.185 2 0.519 1 0.700 8 0.379 2 0.根据文献[8]提供的气体参数u0(平衡位置的势能的大小)和σ(排斥势与吸引势的绝对值相等点)的值,利用关系式可计算出平衡位置r0、f(r)的极值点0.224 16),平衡位置处分子受到的斥力f0斥的值,见表1.2.4 伦纳德—琼斯势的近似相对势能曲线令式(18)中的m=6、n=12,可得伦纳德-琼斯势在平衡位置附近的近似相对势能为其成立条件为X≪1.由它所绘制的雷纳德-琼斯势的近似相对势能曲线如图3中的实线所示.从图3可知,近似的相对势能曲线也是不对称的,平衡位置(X=0)的左边较陡,右边较平坦.2.5 伦纳德—琼斯势的近似相对分子力曲线令式(25)中的m=6、n=12,可得伦纳德-琼斯势在平衡位置附近的近似相对力为由它所绘制的绘制雷纳德-琼斯势的近似相对力曲线如图4中的实线所示.若略去式(32)的第二项,则近似相对力为线性恢复力,其相对力曲线如图4中的虚线所示.由图4可看出,恢复力在平衡位置两边也不对称.当X>0时,恢复力比线性关系所预期的值小,则当X<0时,恢复力比线性关系所预期的值大.即两分子间距增大时,吸引力比线性关系所预期的值小,两分子间距减小时,斥力比线性关系所预期的值大.图3 雷纳德-琼斯势的近似相对势能曲线(虚线为抛物线,对应于势能U(X)=-1+36X2)图4 雷纳德-琼斯势的近似相对力曲线(虚线为直线,对应于线性力F(X)=-6X) 本文引入相对距离R、相对势能U与相对力F,导出了米势的相对势能U(R)及其相应的相对力F(R)与参数n、m的关系,并精确地绘制了伦纳德-琼斯势的相对势能U(R)曲线及其相应的相对力F(R)曲线,形象直观准确地显示了它们的变化规律,弥补了热学、热力学与统计物理学和固体物理学教材中仅给出定性的势能曲线与力曲线的不足.结合文献[8]提供的气体参数u0和σ(r0=)的值,可得出一幅直观、清晰、定量的气体分子间势能u或分子力f随分子间距r变化的图像.另外,还导出平衡位置附近的近似相对势能U(X),相对力F(X)表达式,精确地绘制了伦纳德-琼斯势的近似相对势能曲线、相对力曲线.用简谐近似的方法(F≈-6X),可解释固体的比热问题.若计入非简谐效应(F≈-6X+63X2),可定性或定量[10]解释固体的热膨胀现象.【相关文献】[1]黄淑清,聂宜如,申先甲.热学教程[M].第2版.北京:高等教育出版社,1994:180-185.[2]秦允豪.普通物理学教程热学[M].第3版.北京:高等教育出版社,2011:34-44. [3]李洪芳.热学[M].第2版.北京:高等教育出版社,2001:6-10.[4]汪志诚.热力学·统计物理[M].第2版.北京:高等教育出版社,1993:335-336.[5]李椿,章立源,钱尚武.热学[M].北京:高等教育出版社,1978:59-63.[6]常树人.热学[M].天津:天津大学出版社,2001:89-95.[7]张玉民.热学[M].第2版.北京:科学出版社,2006:6-9.[8]梁希俠,班士良.统计热力学[M].第2版.北京:科学出版社.2008.114-115.[9]蒋平,徐至中.固体物理学简明教程[M].上海:复旦大学出版社.2000.93-96.[10]夏清华.含x2项非线性振子运动的研究[J].大学物理2005,24(4)):6-7.。


热学公式1.3.1物态方程:(1.1)1.3.2体积膨胀系数、压缩系数、压强系数:(1.3)(1.4)(1.5)1.3.3理想气体(压强趋于零的极限状态下的气体/能严格满足理想气体物态方程的气体)物态方程:pV=vRT (1.7)1.3.4混合理想去气体物态方程:(1.9)1.4.3温标:T(p)=(其中不变) (1.10)(1.11)=(体积不变) (1.12)(体积不变) (1.13)1.5.1物质由大数分子组成:(1.14)法拉第常量F=分子热运动:(1.15)1.6.1理想气体微观模型:洛喜密脱常量(1.16)1.6.2单位时间内在单位面积器壁上平均分子数(1.18) (1.19)1.6.3理想气体压强公式:(1.20)(1.21)P=P=(1.23)K=(1.24)1.6.4温度的微观意义:(1.25)气体分子的平均根速度:=(1.26) 1.7.1分子间互作用势能曲线:d(1.29)或F=(1.30)令r时=0 则(1.31) 1.7.2分子碰撞有效直径、固体分子热震动、固体热膨胀:d=分子碰撞有效直径(1.31)1.7.3范德瓦尔斯方程:p=(1.33) (1.34)方程为:(1.43)2.2.2等概率性与概率的基本性质:(2.1)2.2.3平均值及其运算法则:(2.2)n(2.3)2.3.2麦克斯韦速率分布:f(v)dv=4(2.13)三种速率:(1)平均速率:==(2.14)(2)平均根速度:(2.15)(3)最概然速率(2.16)三种速率的比:(2.17) 2.4.1速度空间:f((2.20)2.4.2麦克斯韦速度分布:(2.26) 2.6.1等温大气压强公式:p(z)=p(0)) (2.61)2.7.1理想气体热容:C=(2.75)2.7.3能量均分定理:(2.81)3.1.1牛顿粘性定律:f=3.2.1菲克定律(3.10)3.3.1傅力叶定律:(3.14)热流密度:(3.15)3.8.1气体黏性系数导出:=(3.62)3.8.2气体的导热系数:K=(3.67)气体的扩散系数:D=(3.69)4.2.2体积膨胀功:W=(对外界系统所做的总功)(4.3)理想气体在几种可逆过程中功的计算:(1)等温过程:W=(2)等压过程:W=(3)等体过程:W=04.3.2内能定理:(4.12)热力学第一定律一般表达式:无限小过程第一定律表达式:dU=dQ+dW准静态过程第一定律表达式:dU=dQ4.4.1定体热熔:(4,19) (4.20)4.4.2定压热熔与焓:H=U+pV (4.22)4.5.1理想气体内能:(4.33) 4.5.2理想气体的等体、等压、等温过程:(1)等体过程:(4.39)(2)等压过程:Q(4.40)(3)等温过程:(4.42)4.5.3一般绝热过程准静态绝热过程:理想气体绝热过程中功及温度变化:4.5.6多方过程方程:(4.68)多方过程热熔:4.6.1热机效率的定义:=(4.81)(4.82) (4.83) 4.6.2卡诺热机的效率:(4.90)4.7.1制冷系数:(4.99)卡诺制冷剂效率:(4.100)5.3.1克劳休斯等式:=05.3.2熵和熵的计算:TdS=(5.23)熵的微分表达式以熵来表示热熔(5.25)(5.26)理想气体的熵:(5.29)5.3.7热力学第二定律表达式:热力学基本方程:热学习题课(2007.4.18) Ⅰ教学基本要求气体动理论及热力学1.了解气体分子热运动的图象。