RC电路响应和三要素法

§ 5.4 —阶电路的全响应与三要素在上两节中分别研究了一阶电路的零输入响应和零状态响应， 电路要么只有外激励源的作用，要么只存在非零的初始状态，分析过程相对简单。

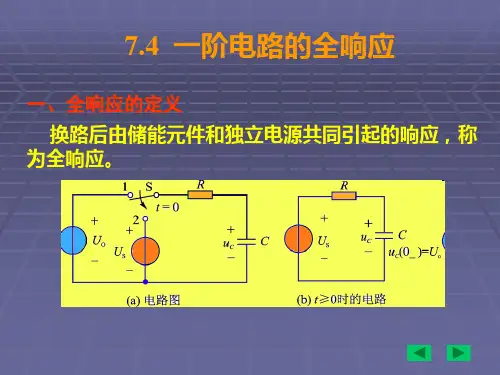
本节将讨论既有非零初始状态，又 有外激励源共同作用的一阶电路的响应，称为一阶电路的全响应。

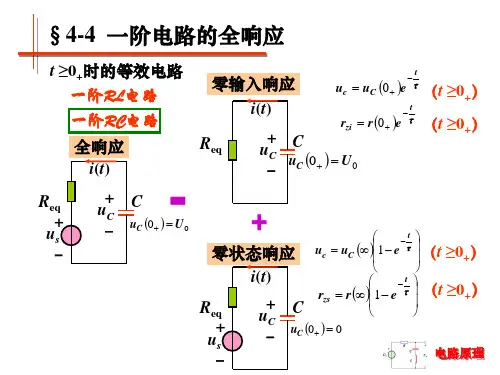
5.4.1 RC 电路的全响应电路如图5-9所示，将开关 S 闭合前，电容已经充电且电容电压u c （0」二U 0，在t=0时将开关S 闭合，直流电压源 U S 作用于一阶RC 电路。

根据KVL 此时电路方程可表示为：U C图5-19 一阶RC 电路的全响应u e(0•) = u e (0 _) = U o 令方程（5-9 ）的通解为U e 二U e U C与一阶RC 电路的零状态响应类似，取换路后的稳定状态为方程的特解，则U e =U St同样令方程（5-9）对应的齐次微分方程的通解为 U C = Ae^。

其中.二RC 为电路的时间常数，所以有tu e =U S Ae":将初始条件与通解代入原方程，得到积分常数为A 二U 。

U S所以电容电压最终可表示为tU c =U S (U 0-U s )e 「(5-20)电容充电电流为due U S _ U 0 -■ i = CdtR e这就是一阶RC 电路的全响应。

图5-20分别描述了 U s ，U 0均大于零时，在U s ・U 0、根据换路原则，可知方程（RCdu e dtU e =U S(5-19)5-19 ）的初始条件为U s = 0、U s :: U 0三种情况下u c 与i 的波形。

（a ） （b ）图5-20 u c ，i 的波形图将式（5-20 ）重新调整后，得ttu c 二U °e 「U s CI-e 「）从上式可以看出，右端第一项正是电路的零输入响应，第二项则是电路的零状态响应。

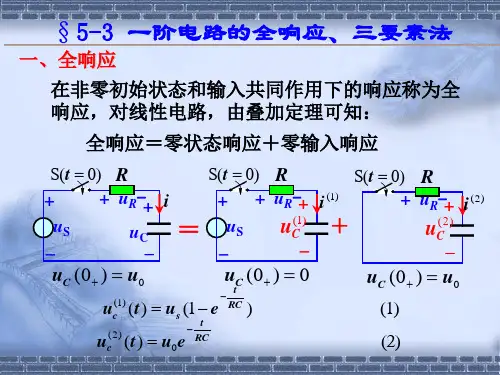
显然，RC 电路的全响应是零输入响应与零状态响应的叠加，即全响应=零输入响应 +零状态响应研究表明，线性电路的叠加定理不仅适用于 RC 电路，在RC 电路的分析过程中同样适用，同时，对于n 阶电路也可应用叠加定理进行分析。

RC与RL电路响应诠析最近在复习电工的时候开始在学的时候因为书上都有RC电路的零输入响应、RC电路的零状态响应、RC电路的全响应这三种情况的分别得公式，我在做题的时候发现这个办法不但记得不是很牢固而且要判断是属于那种情况，费劲。

在看到三要素分析法的时候我就在想是不是这三种情况都是从这个里面衍生出来的。

我就尝试着把每种情况的公式带入到三要素法里面匹配，结果是在意料之中的匹配上了。

RC电路的响应RC零输入响应：其状态图如上图所示：书上直接说其电压值为：Uc=Uoe^(-1/RC) ，电流理所当然的为Uc/ R.这样讲不但抽象而且有点脱节。

三要素法的公式为：f（oo）+（f（0+）-f(oo)）e^(-1/Rc) 注（f（00）代表的是无穷大的时候的f函数，俺不会打）。

用三要素法分析上题为Uc（o+）=U，Uc（oo）=0，（无穷大的时候开关s打到档位1，电容是储电元件，总有放完的时候）带入到三要素公式为：0+(U-0)e^(-1/Rc) 其结果与上面的结果是一致的，我将这个公式带入到例题求解，结果是正确的。

上面的公式为什么不用电流求解呢？电流也是使用于三要素的公式，在RC电路中分析电压要比分析电流要简单的多，我们为什么要避简求繁，用电压的值处以电阻的值不就得到电流的值了。

RC电路的零状态响应；RC零状态响应是在0时刻时电容是处于无电的状态，在t>0的时候的合上开关，用三要素法分析为：在时间0的时候开关没合上，电压U（o+）=0;合上开关后为：U(oo)=E/(R1+R2),即Uc=U（oo）+（U（o+）—U(oo)）=U(oo)(1-e^(-1/RC))与书上得出的公式是一样的，而且分析起来很简单RC电路全响应：全响应就是在0时刻的时候电容就已经充了电了，然后在电路上引起变化，而后还是有电源的存在的情况，其实就是上面两种情况的合成：但是用三要素发求出0时刻的电压和稳定后的电压就不用分别求两种情况的电压了，这使得解题的过程变得简单化了。

一阶RC电路的暂态过程 - 电子技术分析一阶RC电路的暂态过程的方法有很多种，这里只介绍经典法和三要素法，下面以图3-6所示的电路为例，对这两种方法分别进行介绍。

1、经典法图3-6所示电路，t=0时开关S闭合，电源对电容充电，从而产生过渡过程。

根据KVL，得回路电压方程为而：从而得微分方程：此微分方程的通解为两个部分：一个是特解，一个是齐次方程式的解，即:特解可以是满足方程式的任何一个解，假定换路后，t→时电路已达稳定，电容C的电压为稳态分量，那么它是满足方程式的一个解。

对于图3－6所示的RC串联电路：=＝US。

微分方程的齐次方程式为：令其通解为，代入齐次微分方程式可得特征方程式是：所以，特征方程式的根为：式中，其量纲为（秒），称为电路暂态过程的时间常数。

因此微分方程的通解=+积分常数A需用初始条件来确定。

在t=0时=+=+A由此可得：A=-因此+上述利用微分方程进行求解分析一阶RC电路的暂态过程的方法称为经典法，经典分析法步骤较多，为便于掌握，现归纳如下：（1）用基尔霍夫定律列出换路后电路的微分方程式。

（2）解微分方程。

解微分方程通常比较麻烦，对于一阶RC电路有一种更方便、更常用的分析方法——三要素法。

2、三要素法通过经典分析法我们得到图3-6所示电路暂态过程中电容电压为： +上述结果可归纳为一种简单的解题方法，称为“三要素法”，式中只要知道稳态值，初始值和时间常数，这“三要素”，则便被唯一确定。

这种利用“三要素”来实现电路暂态分析的方法，称“三要素法”。

虽然上述式子由图3-6所示的电路提出，但它适合于任何含一个储能元件的一阶电路在阶跃（或直流）信号激励下的过程分析。

而经典法则适用于任何线性电路的暂态分析。

在“三要素”中，特别要注意时间常数，前面已定义，一阶RC电路仅有一个电容元件，C即为电容器的电容量，而R为换路后的电路中除去电容后所得无源二端口网络等值电阻。

下面以直流(激励源为常数)一阶电路为例应用“三要素法”分析电路的响应。

三要素法求一阶电路全响应证明好嘞，今天咱们聊聊一阶电路的全响应，听起来有点高大上，但其实就像喝水一样简单。

先说说什么是一阶电路，简单来说，就是那些只包含一个电感或一个电容的电路。

就好比你家里的水管，要么是直的，要么有个弯头，没啥复杂的。

电路响应嘛，顾名思义，就是电路对输入信号的反应。

咱们要用三要素法来求它，听起来神秘，但其实就是记住三样东西，轻松愉快。

电路里总有个电压源，就像家里有电灯，没电源的电路就像没电的灯，啥也干不了。

我们要知道电路的初始状态，想象一下你刚起床，头发乱七八糟，睁不开眼，那时候你就像一个电路的初态。

我们得搞清楚，这时候电压和电流是什么样的。

电路的状态方程就像你做饭的配方，得先量好材料。

咱们用基尔霍夫定律，这就像你家人争抢遥控器时的规则，谁先抢到，谁就能看电视。

要把这些公式整理一下。

这里的计算过程就像是做一道数学题，心里有个谱，按部就班。

算出来的结果就是电路在某一时刻的状态。

这里面有个关键的地方，时间常数，它就像你的闹钟，一响就能把你叫醒。

时间常数越大，电路的反应越慢，仿佛你还在梦中打转，不愿意醒过来。

反之，时间常数越小，反应速度就快，像个喝了咖啡的年轻人，瞬间就清醒了。

然后，我们得用到强迫响应和自然响应。

强迫响应就像你被老板叫去加班，没得选，只能硬着头皮上班；自然响应就像放假了，终于可以自在地享受生活。

这两者结合起来，就是电路的全响应。

也就是说，我们的电路既要应对外部的电压源，又要考虑到内部的电流状态。

咱们把这两部分结合起来，得到的就是电路的全响应，这就像一盘美味的拼盘，各种口味交融在一起，才叫个美。

大家可能会想，为什么要用三要素法？这就像咱们做菜的时候，要有食材、火候和调味，缺一不可。

三要素法让我们从不同的角度看待问题，找到解决方案。

就算你是个新手，只要有这三样东西，也能做出一桌好菜。

用这个方法求电路全响应，简直是小菜一碟，谁都能搞定。

咱们回顾一下，电路的初始状态、状态方程和时间常数这三样东西，不仅能帮助你求解全响应，还能让你在电路的海洋里遨游自如。

Chapter 7 一阶电路主要内容1.动态电路的方程及其初始条件；2.一阶电路（RC 电路、RL 电路）的时间常数；3.零输入响应、零状态响应、全响应、瞬态分量、稳态分量；4.三要素法；5.阶跃响应、冲激响应。

§7-1 动态电路的方程及其初始条件一、动态电路的方程1.动态电路：含有动态元件（电容或电感）的电路。

2.动态电路的方程： 电路中有储能元件（电容或电感）时，因这些元件的电压和电流的约束关系是通过导数（或积分）表达的。

根据KCL 、KVL 和支路方程式（VAR ）所建立的电路方程是以电流、电压为变量的微分方程或微分-积分方程。

一阶动态电路：仅含一个动态元件的电路（RC 电路、RL 电路）。

3.动态电路的特征：当电路的结构或元件的参数发生改变时（如电源或无源元件的断开或接入，信号的突然注入等），可能使电路改变原来的工作状态，而转变到另一个工作状态。

换路：电路或参数的改变引起的电路变化。

0=t ：换路时刻，换路经历的时间为 0_ 到 +0；-=0t ：换路前的最终时刻； +=0t ：换路后的最初时刻；4.经典法（时域分析法）：根据KCL ，KVL 和VAR 建立描述电路的以时间为自变量的线性常微分方程，然后求解常微分方程，从而得到所求变量（电流或电压）的方法。

用经典法求解常微分方程时，必须根据电路的初始条件确定解答中的积分常数。

电路独立初始条件：)0(+C u 和 L i )0(+。

二、电路的初始条件1.电容的电荷和电压⎪⎪⎩⎪⎪⎨⎧+=+=⎰⎰ξξξξd tt i C t u t u d tti t q t q C C C C C C 0000)(1)()()()()(取 +-==0 ,00t t , 则⎪⎩⎪⎨⎧+=+=⎰⎰+-+--+-+ξξξξd i c u u d i q q C C C C C C 0000)(1)0()0()()0()0(若有限）( M i C ≤， 则 0)(00=⎰+-ξξd i C ，且⎩⎨⎧==-+-+)0()0()0()0(C C C C u u q q 电容上电荷和电压不发生跃变！① 若 -=0t 时，0)0(q q C =-, 0)0(U u C =-, 则有 0)0(q q C =+,)0(U u C =+, 故换路瞬间，电容相当于电压值为 0U 的电压源；② 若 -=0t 时，0)0( ,0)0(==--C C u q , 则应有)0( ,0)0(==++C C u q , 则换路瞬间，电容相当于短路。

一阶电路的三要素法公式
其中：
- f(t)为电路中所求的响应（电压或电流）。

- f(0_+)为响应的初始值，即换路后瞬间t = 0_+时的值。

- f(∞)为响应的稳态值，即t→∞时的值。

- τ为一阶电路的时间常数，对于RC电路τ = RC，对于RL电路τ=(L)/(R)（这里R为从储能元件（电容C或电感L）两端看进去的戴维南等效电阻）。

在使用三要素法求解一阶电路时，一般按照以下步骤：
1. 求初始值f(0_+)：
- 首先根据换路前的电路（t = 0_-时的电路）求出储能元件（电容电压
u_C(0_-)或电感电流i_L(0_-)）的初始值。

- 然后根据换路定律（u_C(0_+) = u_C(0_-)，i_L(0_+)=i_L(0_-)）确定换路后瞬间电容电压和电感电流的值。

- 再根据换路后瞬间的电路（t = 0_+时的电路），利用电路的基本定律（如欧姆定律、基尔霍夫定律等）求出所求响应的初始值f(0_+)。

2. 求稳态值f(∞)：
- 画出换路后t→∞时的电路，此时电容相当于开路（i_C(∞)=0），电感相当于短路（u_L(∞)=0）。

- 利用电路的基本分析方法（如电阻的串并联化简、欧姆定律、基尔霍夫定律等）求出所求响应的稳态值f(∞)。

3. 求时间常数τ：
- 对于RC电路，τ = RC，其中R为从电容两端看进去的戴维南等效电阻。

- 对于RL电路，τ=(L)/(R)，其中R为从电感两端看进去的戴维南等效电阻。

最后将f(0_+)、f(∞)和τ代入三要素法公式f(t)=f(∞)+[f(0_+) - f(∞)]e^-(t)/(τ)中，即可求出一阶电路的响应f(t)。