第六章 纯晶体的凝固

第6章单组元相图及纯晶体的凝固6.1 复习笔记一、单元系相变的热力学及相平衡1．相平衡条件和相律组元：组成一个体系的基本单元，如单质（元素）和稳定化合物，称为组元。

相：体系中具有相同物理与化学性质的且与其他部分以界面分开的均匀部分，称为相。

相律：F=C－P+2；式中，F为体系的自由度数，它是指不影响体系平衡状态的独立可变参数（如温度、压力、浓度等）的数目；C为体系的组元数；P为相数。

常压下，F=C－P＋1。

2．单元系相图单元系相图是通过几何图像描述由单一组元构成的体系在不同温度和压条件下可能存在的相及多相的平衡。

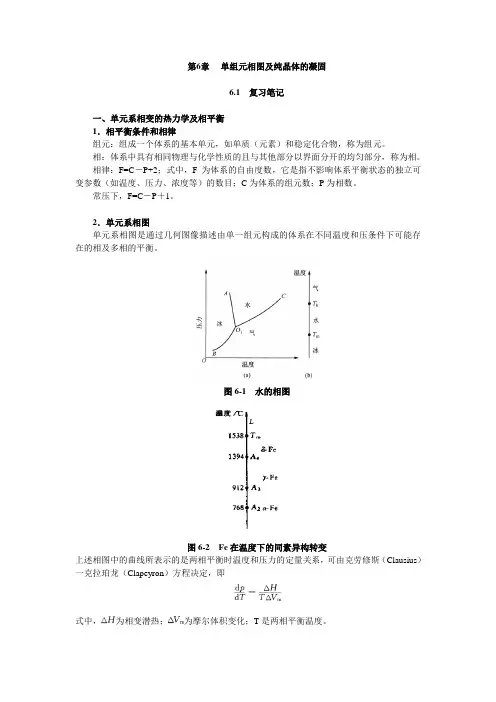
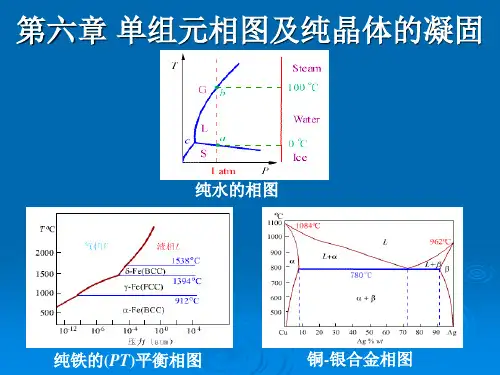
图6-1 水的相图图6-2 Fe在温度下的同素异构转变上述相图中的曲线所表示的是两相平衡时温度和压力的定量关系，可由克劳修斯（Clausius）一克拉珀龙（Clapeyron）方程决定，即式中，为相变潜热；为摩尔体积变化；T是两相平衡温度。

有些物质在稳定相形成前，先行成自由能较稳定相高地亚稳定相。

二、纯晶体的凝固1．液态结构（1）液体中原子间的平均距离比固体中略大；（2）液体中原子的配位数比密排结构晶体的配位数减小；（3）液态结构的最重要特征是原子排列为长程无序，短程有序，存在结构起伏。

2．晶体凝固的热力学条件（6.1）式中，，是熔点T m与实际凝固温度T之差；L m是熔化热。

晶体凝固的热力学条件表明，实际凝固温度应低于熔点T m，即需要有过冷度△T。

3．形核晶体的凝固是通过形核与长大两个过程进行的，形核方式可以分为两类：均匀形核和非均匀形核。

（1）均匀形核①晶核形成时的能量变化和临界晶核新相晶核是在母相中均匀地生成的，即晶核由液相中的一些原子团直接形成，不受杂质粒子或外表面的影响假定晶胚为球形，半径为r，当过冷液中出现一个晶胚时，总的自由能变化：（6.2）由，可得晶核临界半径：（6.3）代入公式（1），可得：（6.4）由式可知，过冷度△T越大，临界半径则越小，则形核的几率越大，晶核数目增多。

082064《材料科学基础》课程考试大纲一、考试方法和考试时间《材料科学基础》课程考试为闭卷笔试、考试时间为120分钟。

二、考试的基本要求使学生掌握材料基础理论知识，诸如材料的结合键、晶体结构、相结构、晶体结构缺陷、材料的相图、凝固、材料中的扩散，材料的塑性变形与强化等。

重点掌握晶体学基础知识，晶面指数与晶向指数，纯金属的晶体结构及特征，材料的相结构，离子晶体的结构规则，共价晶体的结构，高分子材料的结构；晶体结构缺陷（包括点缺陷、线缺陷和面缺陷）的特征，位错的柏氏矢量、类型、判断、运动、能量及交互作用，各类面缺陷；扩散现象和条件，扩散方程、扩散方程的解及其应用，扩散的微观机制，扩散驱动力，扩散的分类和影响扩散的因素；滑移与孪晶变形，纯金属及合金的变形强化，冷变形金属的回复与再结晶，金属的热变形、动态回复再结晶；相律及应用，纯金属的结晶理论、晶核的形成、晶核的成长；匀晶相图、共晶相图、包晶二元相图的分析；铁碳相图；固溶体的凝固理论、共晶合金的凝固理论；三元相图。

三、考试内容和要求第一章原子的结构与键合原子间的结合键的类型和特点，原子间的结合键对材料性能的影响。

第二章固体结构（以金属材料为主）一些概念和术语，晶体学基础知识，晶面指数、晶向指数的标注，晶面间距和晶带定理，三种典型晶体结构（bcc、fcc、hcp）的特征；固溶体的分类、特点和性质，影响固溶体固溶度的因素，中间相的类型和特点；离子（硅酸盐晶体）晶体、共价晶体的特点。

第三章晶体缺陷一些概念和术语，晶体结构缺陷（包括点缺陷、线缺陷和面缺陷）的特征，点缺陷的类型、特征和平衡浓度公式；位错类型（刃型、螺型、混合型位错）的判断及其特征，柏氏矢量的意义及特征，位错的运动、交割和增殖(F-R源、双交滑移机制等)，位错分解与合成，位错的能量及交互作用；各类面缺陷的类型和特征。

第四章固体中原子和分子的运动一些概念和术语，扩散条件，扩散方程、扩散方程的解及其应用，扩散的原子理论（微观机制），扩散驱动力，扩散的分类和影响扩散的因素；离子晶体中的扩散的特点。

《材料结构》习题：纯晶体的凝固1. 设均匀形核时其晶核为球形，试证明临界形核功ΔG c 与临界晶核体积V c 的关系为：12c c V G V G ∆=-∆ 2. 设非均匀形核时其晶核为球冠形，试证明临界形核功*c G ∆与临界晶核体积*c V 也存在上列关系式。

3. 当临界晶核为球形和小立方体形时，试分别求出各临界晶核中的原子数n 的表达式：n =f (ΔG V , σ,V)式中V 为每个原子的体积。

4. 试说明金属结晶时粗糙型液－固界面的微观结构特点，指出该界面在结晶过程中的作用。

5. 综述金属结晶的热力学条件、动力学条件、能量条件和结构条件。

6. 已知金的熔点Tm 为1063℃，熔化潜热Lm 为12.8kJ/mol ，密度为19.3g/cm3，摩尔质量为197g/mol 。

若液态金在1000℃均匀形核时的临界晶核半径r ＝43.3×10-10m ，试计算金的液固界面能σ和临界形核功。

7. 根据克拉珀龙方程可以推导出液－固或固－固相变温度与压力的关系式： T V T H P mm m ∆∆∆=∆ 式中，ΔH m 为相变潜热；T m 为相变温度；ΔV m 为摩尔体积变化。

试分别计算：(1) 已知α-F e →γ-Fe 在1大气压下T m ＝912℃，若外加压力增加到1000大气压时，转变温度应是多少（已知ΔH m ＝920.5J/mol ，α-F e 的密度为7.57g/cm 3，γ-Fe 的密度为7.63g/cm 3，Fe 的摩尔质量为55.85g/mol ）。

(2) 已知纯铁熔化时体积变化为膨胀3％，求10个大气压下的熔点（已知L m ＝15.2kJ/mol ，T m =1803K ，密度为7.6g/cm 3，摩尔质量为55.85g/mol ）。

习题答案1. 证明：设均匀形核时其球形晶核半径为r ，则32232344304802242143232V V V c Vc V c V c c V c c V c V G V G A r G r G r G rr G r G r G G r G r r G V G σππσππσσσπππ∆=∆+=∆+∂∆=⇒∆+∂∆∴=-=-∆∆∴∆=∆-=-∆=-∆令 ＝ 即2．证明：设非均匀形核时其球冠状晶核的曲率半径为r ，高为h ，则系统总表面自由能的增量ΔG S 为S L L W W LW LW G A A A A αααασσσσ∆==+-∑因为晶核周边表面张力应彼此平衡，则cos LW W L αασσσθ=+ 即cos W LW L αασσσθ-=-222(1cos )L A rh r αππθ==-222(sin )(1cos )W A r r απθπθ==-222S 232(1cos )(1cos )cos (23cos cos )L L L G r r r αααπθσπθσθπσθθ∆=---=-+ 球冠的体积 23311(3)(23cos cos )33V r h h r ππθθ=-=-+ 令31()(23cos cos )4f θθθ=-+ **3*24()4()3V S V L G V G G r G f r f απθπσθ∆=∆+∆=∆+则 **2**04()8()0c V c L G r G f r f rαπθπσθ∂∆=⇒∆+∂令 ＝ ****22L c c cL V r G r G αασσ∆∴=-=-∆ 即 ****3**2*3*424()()323c V cc V c c V r G G r G r f r G f ππθπθ⎛⎫∆∴∆=∆-=-∆ ⎪⎝⎭ **3***41()32c c c c V V r f G V G πθ=∴∆=-∆3．解: (1)当临界晶核为球形时，设其半径为r c ，则33333243233323c c c V Vc V r V r G G V n V G V σπσππσ=-∴==-∆∆∴==-∆(2)当晶核为正方形时，设其边长为a ，则326V V G V G A a G a σσ∆=∆+=∆+2403120c V c c VG a G a a r G σσ∂∆=⇒∆+=-∂∆令 ＝，即 333336464c c c V V V V a n V G V G σσ=∴==-=-∆∆4．答：金属结晶时粗糙型液－固界面的微观结构为粗糙界面。

内容提要由一种元素或化合物构成的晶体称为单组元晶体或纯晶体，该体系称为单元系。

某组元由液相至固相的转变称为凝固。

如果凝固后的固体是晶体，则凝固又称为结晶。

研究纯晶体的凝固，首先必须了解晶体凝固的热力学条件。

在恒压条件下，晶体凝固的热力学条件是需要过冷度，即实际凝固温度应低于熔点T m。

晶体的凝固经历了形核与长大两个过程。

形核又分为均匀形核与非均匀（异质）形核。

对于均匀形核，当过冷液体中出现晶胚时，一方面，体系的体积自由能下降，这是结晶的驱动力；另一方面，由于晶胚构成新的表面而增强了表面自由能，这成为结晶的阻力。

综合驱动力和阻力的作用，可导出晶核的临界半径r*，其物理意义是，当半径小于r*的晶胚是不稳定的，不能自发长大，最终熔化而消失，而半径等于或大于r*的晶胚可以自发长大成为晶核。

临界半径对应的自由能称为形核功。

理论推导表明，是大于零的，其值等于表面能的三分之一，因此，这部分的能量必须依靠液相中存在的能量起伏来提供。

综合所述可知，结晶条件需要过冷度、结构起伏（出现半径大于r*的晶胚）和能量起伏。

在研究结晶问题时，形核率是一个重要的参数，它涉及到凝固后的晶粒的大小，而晶粒尺寸对材料的性能有重要影响。

形核率受两个因素控制，即形核功因子核和扩散几率因子。

对纯金属均匀形核研究发现，有效形核温度约在0.2T m，表明均匀形核所需的过冷度很大。

而纯金属在实际凝固中，所需过冷度却很小，其原因是实际凝固是非均匀（异质）形核。

异质基底通常可有效地降低单位体积的表面能，从而降低形核功，这种异质基底的催化作用使非均匀（异质）形核的过冷度仅为0.02T m。

形核后地长大涉及到长大的形态、长大的方式和长大的速率。

影响晶体长大特征的重要因素是液——固界面的构造。

液——固界面的结构可分为光滑界面和粗糙界面。

晶体的长大速率与其长大方式有关。

连续长大方式对应的是粗糙界面，其长大速率最大，与动态过冷度（液——固界面向液体推移时所需的过冷度）成正比；而二维形核+z长大（螺形位错形核对应）是光滑界面，它们的生长速率均小于连续长大方式的生长速率。

晶体凝固过程晶体凝固是物质从液态到固态的转变过程，也是自然界中常见的现象之一。

从我们日常生活中可以观察到的冰冻水变成冰块，到金属加工中铸造出的铁锭，都是晶体凝固的例子。

本文将从晶体凝固的基本原理、凝固方式和凝固过程中的影响因素等方面进行探讨。

晶体凝固的基本原理是物质分子在冷却过程中逐渐失去热能并排列有序，形成具有周期性结构的晶体。

在液态的物质中，分子之间的相互作用较弱，可以自由运动。

而当温度下降时，分子的热运动减弱，分子之间的相互作用逐渐增强，最终达到一种平衡状态，形成有序的晶体结构。

晶体凝固的方式有两种：均匀凝固和非均匀凝固。

均匀凝固是指整个液体体系同时凝固，在凝固过程中晶体的生长速度相对均匀。

而非均匀凝固则是指液体体系在局部区域先行凝固，形成初生晶核，然后晶体的生长从这些初生晶核开始扩展。

非均匀凝固常见于铸造、合金制备等工艺中。

晶体凝固过程中的影响因素有很多，其中温度是最重要的因素之一。

温度的升高可以加快晶体凝固过程，而温度的降低则会使晶体凝固速度变慢。

此外，溶液中的浓度和成分也会对晶体凝固过程产生影响。

浓度的增加会使晶体生长速度加快，而溶液中的杂质则会抑制晶体的生长。

晶体凝固过程的速度还受到晶体生长界面的形态和形态变化的影响。

晶体生长界面的形态决定了晶体的外形和晶体的生长速度。

例如，面心立方结构的晶体生长界面是六角形的，而体心立方结构的晶体生长界面则呈现出立方形。

晶体生长界面的形态变化会导致晶体生长速度的改变。

晶体凝固过程除了在材料科学中有着广泛应用外，还在生物学、地质学等领域中有重要作用。

例如，在生物学中，晶体凝固是生物体中骨骼和牙齿等硬组织形成的基础。

在地质学中，晶体凝固是岩石形成的过程之一，不同的岩石类型由不同的晶体凝固方式形成。

晶体凝固是物质从液态到固态的转变过程，涉及到物质分子的有序排列和晶体生长等过程。

它是自然界中常见的现象，对于材料科学、生物学和地质学等领域都具有重要意义。

通过研究晶体凝固过程的原理、方式和影响因素，可以更好地理解物质的结构和性质，为相关领域的发展提供科学依据。

晶体凝固过程晶体凝固是一种物质由液态到固态的转变过程，它是自然界中晶体形成的基础过程。

晶体凝固过程发生在许多不同的领域，如冶金、材料科学、地质学、化学等。

本文将从晶体凝固的原理、过程和应用三个方面来详细介绍晶体凝固的相关内容。

一、晶体凝固的原理晶体凝固的原理可以归结为两个主要因素：热力学驱动力和动力学过程。

热力学驱动力指的是凝固过程中的能量差异，即液态相与固态相之间的自由能差。

当液态相的自由能高于固态相时，晶体凝固就会发生。

动力学过程则是指晶体凝固中的原子或分子在空间上有序排列的过程。

晶体在凝固过程中，原子或分子按照一定的规律有序排列，形成晶体结构。

二、晶体凝固的过程晶体凝固过程可以分为三个阶段：核化、生长和成熟。

1. 核化阶段：在液体中，当达到一定的过饱和度时，原子或分子会聚集形成小的晶核。

晶核的形成是一个热力学过程，需要克服液体的表面张力。

晶核的形成是凝固过程的起点，也是晶体生长的基础。

2. 生长阶段：晶核形成后，它们会在液体中生长。

晶体生长是一个动力学过程，晶体中的原子或分子按照一定的方向和速度有序排列。

晶体生长的速度取决于温度、过饱和度、物质的浓度等因素。

3. 成熟阶段：当晶体生长到一定大小时，晶体就会达到成熟状态。

成熟的晶体具有完整的晶体结构和形态，它们可以继续生长也可以停止生长。

三、晶体凝固的应用晶体凝固在许多领域都有广泛的应用。

1. 冶金领域：晶体凝固技术在冶金中可以用于合金的制备。

通过控制凝固过程中的温度、过饱和度和凝固速度等参数，可以得到具有特定性能的合金材料。

2. 材料科学领域：晶体凝固技术可以用于制备单晶材料，如硅单晶、镁铝合金等。

单晶材料具有优异的物理性能和化学性能，在电子器件、光学器件等领域有重要应用。

3. 地质学领域：晶体凝固是地壳中岩石形成的重要过程。

岩浆在地壳中凝固形成岩石，不同的凝固速度和条件会导致不同的岩石类型。

4. 化学领域：晶体凝固技术可以用于制备纯净的化学物质。