第6章 单组元相图及纯晶体的凝固 笔记及课后习题详解 (已整理 袁圆 2014.8.6)
- 格式:doc
- 大小:4.83 MB
- 文档页数:14



材料科学基础第六章总结与思考题第6、7章总结、思考题与作业题一、本章总结1、凝固与结晶、相变、固态相变、组元、系、相图、单元相图、相平衡、相律(及表达式)及应用2、纯金属凝固的过程和现象;过冷度对结晶过程和结晶组织的影响;3、结晶的热力学条件、动力学条件、能量条件和结构条件;包括:一些更要的公式,以其应用4、过冷现象、过冷度、理论凝固温度、实际凝固温度、临界过冷度、有效过冷度、动态过冷度;5、均匀形核与非均匀形核,二者有何异同点。
结构起伏(相起伏)、能量起伏、浓度起伏、晶胚、晶核、临界晶核、临界晶核半径、临界形核功,临界晶核半径、临界形核功的计算。
形核率及影响因素、变质处理。
非均匀形核时影响接触角θ的因素有哪些?选择什么样的异相质点可以大大促进结晶过程。
6、光滑界面、粗糙界面;正温度梯度、负温度梯度;平面长大、树枝长大。
晶体长大的条件和长大的机制。
界面的生长形态与L/S前沿的温度梯度有何关系?7、能用结晶理论说明实际生产问题。
如:变质处理和其它细化晶粒的工艺;单晶的制取和定向凝固技术。
(1).凝固理论的主要应用;(2).控制结晶组织的措施。
二、本章重要知识点1. 金属结晶的过程;结晶的热力学条件、动力学条件、能量条件和结构条件;2. 界面的生长形态与L/S前沿的温度梯度的关系。
三、思考题1. 简述金属结晶过程的热力学条件、动力学条件、能量条件和结构条件。
为什么需要这些条件?冷却速度与过冷度的关系是什么?能否说过冷度越大,形核率越高,为什么?2. 何谓正温度梯度和负温度梯度。
何谓粗糙界面和光滑界面。
分析纯金属生长形态与温度梯度的关系。
(简述纯金属枝晶的形成条件和长大过程。
)3. 在同样的负温度梯度下,为什么Pb结晶出树状晶,而Si结晶平面却是平整的?4. 何谓均匀形核?何谓非均匀形核(异质形核)?试比较二者有何异同?叙述异质形核的必要条件。
选择什么样的异相质点可以大大促进结晶过程?5. 指出形核过程的驱动力和阻力分别是什么?比较均匀形核和非均匀形核的临界形核功大小和形核率的大小,说明造成两者差异的原因。






第6章单组元相图及纯晶体的凝固物质由液态转变为固态的过程称为凝固。
物质由液态转变为晶态的过程称为结晶材料的性能组织结构相种类数量尺寸形状分布C ONTENTS6.1 单元系相变的热力学及相平衡6.2纯晶体的凝固6.1单元系相变的热力学及相平衡1. 相(Phase)在一个系统中,成分、结构相同,性能一致的均匀的组成部分叫做相,不同相之间有明显的界面分开,该界面称为相界面。
注意:相在物理性能和化学性能上是均匀的。
相界面和晶界的区别。
6.1单元系相变的热力学及相平衡2. 组元(Component)组元通常是指系统中每一个可以单独分离出来,并能独立存在的化学纯物质,在一个给定的系统中,组元就是构成系统的各种化学元素或化合物。
按组元数目,将系统分为:一元系二元系三元系……化学元素:Cu, Ni, Fe 等化合物:Al 2O 3, MgO, Na 2O, SiO 2等6.1单元系相变的热力学及相平衡3. 相平衡在某一温度下,系统中各个相经过很长时间也不互相转变,处于平衡状态,这种平衡称为相平衡。
各组元在各相中的温度、压力和化学势相同。
A B热力学动态平衡6.1单元系相变的热力学及相平衡4.吉布斯相律(Gibbs Phase Rule)处于热力学平衡状态的系统中自由度与组元数和相数之间的关系定律,通常简称为相律。
f = C-P+N只考虑温度和压力对系统平衡状态的影响:f = C-P+2凝聚系统:f = C-P+1式中:f(freedom)是自由度数;C(component)是组成材料系统的独立组元数;P(phase)是平衡相的数目。
吉布斯相律的应用和局限性相律是检验、分析和使用相图的重要工具,利用它可以分析和确定系统中可能存在的相数,检验和研究相图。
注意使用相律有一些限制:(1)只适用于热力学平衡状态,各相温度相等、压力相等、化学势相等(化学平衡)。
(2)只表示体系中组元和相的数目,不能指明组元和相的类型和含量。

凝固4.1.2相律4.1 相图的基本知识相律:在平衡条件下,一个系统的组成物的组元数、相数、和自由度数之间的关系可以由相律来确定。
相律的数学表达式如下:F ——系统的自由度数C ——组成物的组元数P ——系统中能够同时存在的相数2 ——表示温度和压力两个变量,对于不含气相的凝聚体系,压力的影响极小,可以不把压力当作变量而看作常量:1个大气压(atm),因此自由度数减少一个,相律的表达式为:4.1.2 相律☐在压力不变(1atm )的条件下,F = C –P +1 = 2–P。
F = 0的含义是:在保持系统平衡状态不变的条件下,没有可以独立变化的变量。
即,任何变量的变化都会造成系统平衡状态的变化。
◼自由度数F 的最小值为0,当F = 0时,P = 2。
◼这说明,在压力不变(1atm)条件下,单元系统最多只能有二相同时存在。
(表现为??图形)☐如果压力可变,◼F = 0时,由公式F = C -P + 2 可知P = 3,◼单元系统最多可以有三相共存。
(表现为??图形)4.1.2 相律☐在压力不变(1atm)的条件下,F = C–P+1 = 3–P。
◼自由度数F的最小值为0,当F= 0时,P= 3。
◼这说明,当二元合金系统同时出现三个相时,就没有可以变化的因素了☐也就是说,只有在一定的温度、成分所确定的某一点才会出现三相同时存在的状态。
☐表现为??图形4.1.2 相律☐在压力不变(1atm)的条件下,F = C–P+1 = 3–P。
◼可以推断出,二元合金系统存在“三相共存状态”的平衡反应,仅有二大类型:A→B+C,A+B→C。
☐由于自由度数为0,这些平衡反应都是恒温反应,并且反应中的三个相(无论是反应相,还是生成相)的化学成分都是固定的。
☐只有当反应结束后(相数小于3时),随着温度的变化,相的化学成分才可能发生变化。
❶液体中原子间的平均距离比固体中略大;液态结构的特征❷液体中原子的配位数•对于密排结构晶体,液态时配位数减小——导致熔化时体积略为增加,•但对非密排结构的晶体,则液态时配位数反而增大,故熔化时体积略为收缩。
第6章单组元相图及纯晶体的凝固由一种元素或化合物构成的晶体称为单组元晶体或纯晶体,该体系称为单元系。
对于纯晶体材料而言,随着温度和压力的变化,材料的组成相随之而变化。
从一种相到另一种相的转变称为相变,由液相至固相的转变称为凝固,如果凝固后的固体是晶体,则又可称之为结晶。
而由不同固相之间的转变称为固态相变,这些相变的规律可借助相图直观简明地表示出来。
单元系相图表示了在热力学平衡条件下所存在的相与温度和压力之间的对应关系,理解这些关系有助于预测材料的性能。
本章将从相平衡的热力学条件出发来理解相图中相平衡的变化规律。
在这基础上,进一步讨论纯晶体的凝固热力学和动力学问题,以及内外因素对晶体生长形态的影响,鉴于单组元高分子(均聚物)的某些特殊性,本章专列一节"高分子的结晶特征"。
6.1单元系相变的热力学及相平衡6.1.1 相平衡条件和相律组成一个体系的基本单元,例如单质(元素)和化合物,称为组元。
体系中具有相同物理与化学性质的,且与其他部分以界面分开的均匀部分称为相。
通常把具有n个组元都是独立的体系称为n元系,组元数为一的体系称为单元系。
处于平衡状态下的多相(P个相)体系,每个组元(共有C个组元)在各相中的化学势都必须彼此相等。
处于平衡状态的多元系中可能存在的相数将有一定的限制。
这种限制可用吉布斯相律表示之:f=C-P+2式中,f为体系的自由度数.它是指不影响体系平衡状态的独立可变参数(如温度、压力、浓度等)的数目;C为体系的组元数;P为相数。
对于不含气相的凝聚体系,压力在通常范围的变化对平衡的影响极小,一般可认为是常量。
因此相律可写成下列形式:f=C-P+1相律给出了平衡状态下体系中存在的相数与组元数及温度、压力之间的关系,对分析和研究相图有重要的指导作用。
6.1.2 单元系相图单元系相图是通过几何图形描述由单一组元构成的体系在不同温度和压力条件下所可能存在的相及多相的平衡。
现以水为例说明单元系相图的表示和测定方法。
第6章单组元相图及纯晶体的凝固6.1 复习笔记一、单元系相变的热力学及相平衡1.相平衡条件和相律组元:组成一个体系的基本单元,如单质(元素)和稳定化合物,称为组元。
相:体系中具有相同物理与化学性质的且与其他部分以界面分开的均匀部分,称为相。
相律:F=C-P+2;式中,F为体系的自由度数,它是指不影响体系平衡状态的独立可变参数(如温度、压力、浓度等)的数目;C为体系的组元数;P为相数。
常压下,F=C-P+1。
2.单元系相图单元系相图是通过几何图像描述由单一组元构成的体系在不同温度和压条件下可能存在的相及多相的平衡。
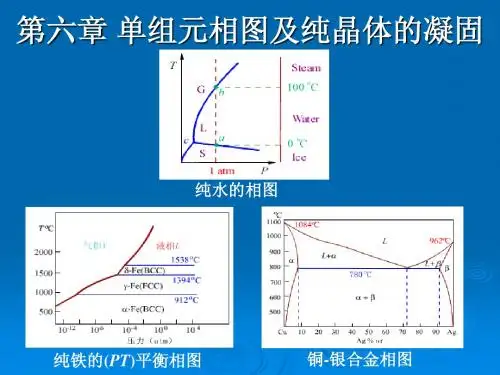
图6-1 水的相图图6-2 Fe在温度下的同素异构转变上述相图中的曲线所表示的是两相平衡时温度和压力的定量关系,可由克劳修斯(Clausius)一克拉珀龙(Clapeyron)方程决定,即式中,为相变潜热;为摩尔体积变化;T是两相平衡温度。
有些物质在稳定相形成前,先行成自由能较稳定相高地亚稳定相。
二、纯晶体的凝固1.液态结构(1)液体中原子间的平均距离比固体中略大;(2)液体中原子的配位数比密排结构晶体的配位数减小;(3)液态结构的最重要特征是原子排列为长程无序,短程有序,存在结构起伏。
2.晶体凝固的热力学条件(6.1)式中,,是熔点T m与实际凝固温度T之差;L m是熔化热。
晶体凝固的热力学条件表明,实际凝固温度应低于熔点T m,即需要有过冷度△T。
3.形核晶体的凝固是通过形核与长大两个过程进行的,形核方式可以分为两类:均匀形核和非均匀形核。
(1)均匀形核①晶核形成时的能量变化和临界晶核新相晶核是在母相中均匀地生成的,即晶核由液相中的一些原子团直接形成,不受杂质粒子或外表面的影响假定晶胚为球形,半径为r,当过冷液中出现一个晶胚时,总的自由能变化:(6.2)由,可得晶核临界半径:(6.3)代入公式(1),可得:(6.4)由式可知,过冷度△T越大,临界半径则越小,则形核的几率越大,晶核数目增多。
将(3)式代入(2)式,得临界形核功:(6.5)将(1)式代入(5)式,可得:(6.6)临界晶核表面积为:(6.7)将(7)式代入(6)式,可得:(6.8)因此,形成临界晶核时体积自由能的减少只能补偿表面能的2/3,而不足的1/3则需依靠液相中存在的能量起伏来补充。
结构起伏和能量起伏是促进均匀形核的必要因素。
②形核率形核率受两个因素的控制,即形核功因子和原子扩散的几率因子,因此形核率为:(6.9)对于易流动液体来说,形核率随温度下降至某值T*时突然显著增大,此温度T*可视为均匀形核的有效形核温度,有效过冷度。
但对于高粘滞性的液体,均匀形核率很小,以致常常不存在有效形核温度。
结论:均匀形核的难度较大。
(2)非均匀形核新相优先在母相中存在的异质处形核,即依附于液相中的杂质或外来表面形核。
在实际溶液中不可避免地存在杂质和外表面(例如,容器表面),因而其凝固方式主要是非均匀形核。
且由于均匀形核难度较大,所以液态金属多为非均匀行核。
非均匀行核时的临界半径为:形核功为:(6.10)由此可见,非均匀形核所需的形核功小于均匀形核功,故非均匀形核所需的过冷度较均匀形核时小,非均匀形核在约为0.02Tm的过冷度时,形核率已达到最大值。
4.晶体长大(1)液-固界面的构造晶体凝固后呈现不同的形状,可分为小平面形状和非小平面形状。
图6-3 小平面状和非平面状按原子尺度,把相界面结构分为粗糙界面和光滑界面两类。
①光滑界面:在界面以上为液相,以下为固相,固相的表面为基本完整的原子密排面,液、固两相截然分开,所以从微观上看是光滑的,但在宏观上它往往由不同位向的小平面所组成,故呈折线状,这类界面也称小平面界面。
②粗糙界面:在固、液两相之间的界面从微观来看是高低不平的,存在几个原子层厚度的过渡层,在过渡层中约有半数的位置为固相原子所占据。
但由于过渡层很薄,因此从宏观来看,界面显得平直,不出现曲折的小平面。
图6-4 (a)光滑界面(b)粗糙界面(2)晶体长大方式和长大速率晶体的长大方式可有连续长大、二维晶核、螺型位错长大等方式:①连续长大:粗糙界面垂直长大;②二维形核,二维形核的生长方式由于其形核较大,因此实际上甚少见到;③螺型位错生长。
图6-5 二维晶核长大机制示意图螺型位错台阶长大机制示意图5.结晶动力学及凝固组织(1)结晶动力学(6.11)上式称为约翰逊一梅尔(Johnson-Mehl )结晶动力学方程,并可应用于在四个条件(均 匀形核,N 和v g 为常数,以及小的τ值)下的任何形核与长大的转变,如再结晶。
1exp()n r φkt =-- (6.12)阿弗拉密方程是描述结晶和固态相变中转变动力学的唯象方程。
(2)纯晶体凝固时的生长形态纯晶体凝固时的生长形态不仅与液—固界面的微观结构有关,而且取决于界面前沿液相中的温度分布情况,温度分布可有两种情况:正的温度梯度和负的温度梯度,分别如图6-6(a ),(b )所示。
图6-6 两种温度分布方式(a)正梯度(b)负梯度①在正的温度梯度下的情况:a.若是光滑界面结构的晶体,其生长形态呈台阶状;b.若是粗糙界面结构的晶体,其生长形态呈平面状。
图6-7 在正的温度梯度下观察到的两种界面形态(a)台阶状(光滑界面结构的晶体)(b)平面状(粗糙界面结构的晶体)②在负的温度梯度下的情况:晶体的生长方式为树枝状生长或树枝状结晶:图6-8 树枝状晶体生长示意图6.凝固理论的应用举例(1)细化晶粒的方法①增加过冷度②加入行核剂③振动促进形核(2)单晶的制备①垂直提拉法:加入籽晶②尖端形核法:自发形核(3)非晶态金属的制备三、气-固相变与薄膜生长1.蒸气压蒸气压:固相与气相形成平衡时的压强称为饱和蒸气压,简称蒸气压。
由热力学克拉珀龙方程可推导出材料蒸气压与温度的关系,即蒸气压方程:(6.13)又可写成:(6.14)2.蒸发和凝聚的热力学条件(6.15)由(6.15)式,当P<P e,ΔG<0,蒸发过程可以进行;当P>P e,则凝聚过程可进行。
3.气体分子的平均自由程气体分子的平均自由程L和气体压强p成反比,在室温时并可近似认为:式中,L单位为mm;P单位为Pa。
通常要求气体分子的平均自由程大于蒸发源到基片距离的10倍。
4.形核材料在镀膜时,高温的蒸发原子飞向未加热的基片,由于原子接触基片后温度急剧降低,此时气体原子的蒸气压也随之快速下降,气体原子将凝聚。
当晶核为球形时,其临界尺寸r c为:,(6.16)气相沉积的形核率受形核功因子和原子扩散几率因子共同影响。
由于气相沉积过冷度很大,因此,形核率主要受形核功因子的影响。
5.薄膜的生长方式①三维生长模型;②二维生长模型;③层核生长模型。
图6-9 薄膜生长的三种类型(a)三维生长(b)二维生长(c)层核生长6.应用举例(1)巨磁电阻多层膜(2)颗粒膜四、高分子的结晶特征1.相似性(1)形核需要过冷度,冷速越快,过冷度越大,球晶的尺寸越小,密度也越大;(2)高分子的结晶过程包括形核和长大两个过程;(3)非均匀形核所需的过冷度较均匀形核小,形核剂能有效地提高形核率;(4)高分子的等温结晶转变量也可用阿弗拉密方程来描述。
2.差异性高分子结晶具有不完全性,高分子结晶的不完全性及其结晶能力的大小起因于大分子链结构的特征。
影响高分子结晶能力的结构因素有:(1)链的对称性:对成型越高,越易结晶;(2)链的规整性:规整构型易结晶(全同、间同、无规立构)(3)共聚效应(无规、交替、嵌段、接枝共聚)(4)链的柔顺性(苯环、支化、交联)由热力学方法可导出熔点和晶片厚度之间的关系:(6.17)晶片越厚,熔点越高。
6.3课后习题详解6-1 计算当压力增加到500×105Pa时锡的熔点变化,已知在105Pa下,锡的熔点为505K,熔化热为7196J/mol,摩尔质量为118.8×10-3kg/mol,固体锡的密度为7.30×103kg/m3,熔化时的体积变化为+2.7%。
答:锡的摩尔体积:假定△V m和△H m在所考虑温度范围内不变,且△T≤T,则:6-2 根据下列条件建立单元系相图:①组元A在固态有两种结构A1和A2,且密度A2>A1>液体;②A1转变到A2的温度随压力增加而降低;③A1相在低温是稳定相;④固体在其本身的蒸气压1333Pa(10mmHg)下的熔点是8.2℃;⑤在1.013×105Pa(1个大气压)下沸点是90℃;⑥A1,A2和液体在1.013×106Pa(10个大气压)下及40℃时三相共存(假设升温相变△H<0)。
答:见下图。
(1)首先根据已知条件作出各交点:a点:固体A1、液体和气体的三相平衡,T=8.2℃,p=1.013×104Pa。
b点:固体A1,A2和液体的三相平衡,T=40℃,p=l.013×106Pa。
c点:液体和气体二相平衡,T=90℃,P=1.013×105Pa。
(2)根据相变时的体积变化,由dp HdT T V∆∆=确定各线斜率及正负。
经过b点的A1和A2相界线:A1→A2,故△H>0,△V<0,故pT∆∆<0,斜率为负;A1和液相L的相界线:A1→L,故△H>0,△V>0,故pT∆∆>0,斜率为正;L和气相g的相界线:L→g,故△H>0,△V>0,故pT∆>∆,斜率为正。
各线的延长线也与以上相同。
所作相图如图27所示。
6-3 考虑在1个大气压下液态铝的凝固,对于不同程度的过冷度,即△T=1,10,100和200℃,计算:①临界晶核尺寸;②半径为r*的晶核个数;③从液态转变到固态时,单位体积的自由能变化△G v;④从液态转变到固态时,临界尺寸r*处的自由能的变化△G r*(形核功)。
铝的熔点T m=993K,单位体积熔化热L m=l.836×109J/m3,固液界面比表面能δ=93×10-3J/m2,原子体积V0=1.66×10-29m3。
答:①临界晶核尺寸,因为△T=T m-T是正值,所以r*为正,将过冷度△T=1K代入,得:②半径为r*的球状晶核数:③④处于临界尺寸r*的晶核的自由能同理,可得△T=10,100和200℃的结果,见下表:6-4 ①已知液态纯镍在1.013×105Pa(1个大气压),过冷度为319℃时发生均匀形核。
设临界晶核半径为1nm,纯镍的熔点为1726K,熔化热L m=l8075J/mol,摩尔体积V=6.6cm3/mol,计算纯镍的液--固界面能和临界形核功。
②若要在2045K发生均匀形核,须将大气压增加到多少?已知凝固时体积变化△V=-。