15材料科学基础第六章__单组元相图及纯晶体的凝固01
- 格式:ppt
- 大小:5.42 MB
- 文档页数:41
第6章单组元相图及纯晶体的凝固6.1 复习笔记一、单元系相变的热力学及相平衡1.相平衡条件和相律组元:组成一个体系的基本单元,如单质(元素)和稳定化合物,称为组元。
相:体系中具有相同物理与化学性质的且与其他部分以界面分开的均匀部分,称为相。
相律:F=C-P+2;式中,F为体系的自由度数,它是指不影响体系平衡状态的独立可变参数(如温度、压力、浓度等)的数目;C为体系的组元数;P为相数。
常压下,F=C-P+1。
2.单元系相图单元系相图是通过几何图像描述由单一组元构成的体系在不同温度和压条件下可能存在的相及多相的平衡。
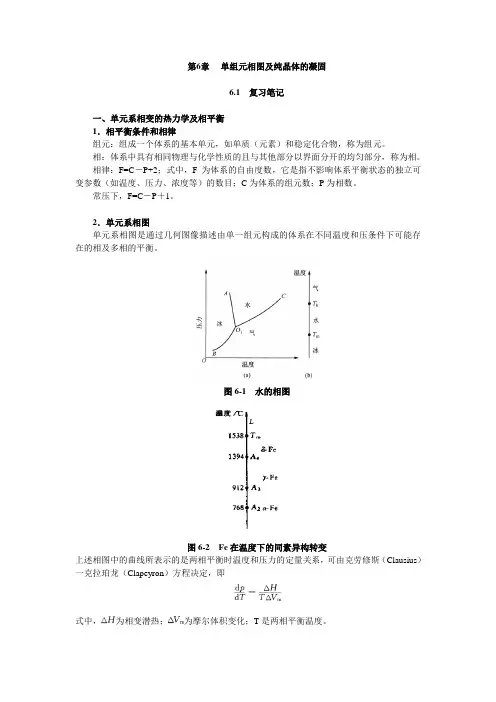
图6-1 水的相图图6-2 Fe在温度下的同素异构转变上述相图中的曲线所表示的是两相平衡时温度和压力的定量关系,可由克劳修斯(Clausius)一克拉珀龙(Clapeyron)方程决定,即式中,为相变潜热;为摩尔体积变化;T是两相平衡温度。
有些物质在稳定相形成前,先行成自由能较稳定相高地亚稳定相。
二、纯晶体的凝固1.液态结构(1)液体中原子间的平均距离比固体中略大;(2)液体中原子的配位数比密排结构晶体的配位数减小;(3)液态结构的最重要特征是原子排列为长程无序,短程有序,存在结构起伏。
2.晶体凝固的热力学条件(6.1)式中,,是熔点T m与实际凝固温度T之差;L m是熔化热。
晶体凝固的热力学条件表明,实际凝固温度应低于熔点T m,即需要有过冷度△T。
3.形核晶体的凝固是通过形核与长大两个过程进行的,形核方式可以分为两类:均匀形核和非均匀形核。
(1)均匀形核①晶核形成时的能量变化和临界晶核新相晶核是在母相中均匀地生成的,即晶核由液相中的一些原子团直接形成,不受杂质粒子或外表面的影响假定晶胚为球形,半径为r,当过冷液中出现一个晶胚时,总的自由能变化:(6.2)由,可得晶核临界半径:(6.3)代入公式(1),可得:(6.4)由式可知,过冷度△T越大,临界半径则越小,则形核的几率越大,晶核数目增多。








凝固4.1.2相律4.1 相图的基本知识相律:在平衡条件下,一个系统的组成物的组元数、相数、和自由度数之间的关系可以由相律来确定。
相律的数学表达式如下:F ——系统的自由度数C ——组成物的组元数P ——系统中能够同时存在的相数2 ——表示温度和压力两个变量,对于不含气相的凝聚体系,压力的影响极小,可以不把压力当作变量而看作常量:1个大气压(atm),因此自由度数减少一个,相律的表达式为:4.1.2 相律☐在压力不变(1atm )的条件下,F = C –P +1 = 2–P。
F = 0的含义是:在保持系统平衡状态不变的条件下,没有可以独立变化的变量。
即,任何变量的变化都会造成系统平衡状态的变化。
◼自由度数F 的最小值为0,当F = 0时,P = 2。
◼这说明,在压力不变(1atm)条件下,单元系统最多只能有二相同时存在。
(表现为??图形)☐如果压力可变,◼F = 0时,由公式F = C -P + 2 可知P = 3,◼单元系统最多可以有三相共存。
(表现为??图形)4.1.2 相律☐在压力不变(1atm)的条件下,F = C–P+1 = 3–P。
◼自由度数F的最小值为0,当F= 0时,P= 3。
◼这说明,当二元合金系统同时出现三个相时,就没有可以变化的因素了☐也就是说,只有在一定的温度、成分所确定的某一点才会出现三相同时存在的状态。
☐表现为??图形4.1.2 相律☐在压力不变(1atm)的条件下,F = C–P+1 = 3–P。
◼可以推断出,二元合金系统存在“三相共存状态”的平衡反应,仅有二大类型:A→B+C,A+B→C。
☐由于自由度数为0,这些平衡反应都是恒温反应,并且反应中的三个相(无论是反应相,还是生成相)的化学成分都是固定的。
☐只有当反应结束后(相数小于3时),随着温度的变化,相的化学成分才可能发生变化。
❶液体中原子间的平均距离比固体中略大;液态结构的特征❷液体中原子的配位数•对于密排结构晶体,液态时配位数减小——导致熔化时体积略为增加,•但对非密排结构的晶体,则液态时配位数反而增大,故熔化时体积略为收缩。

材料科学基础-单组元相图及纯晶体的凝固(总分:110.00,做题时间:90分钟)一、论述题(总题数:11,分数:110.00)1.计算当压力增加到500×105Pa时锡的熔点变化,已知在105Pa下,锡的熔点为505K,熔化热为7196J/mol,摩尔质量为118.8×10-3kg/mol,固体锡的密度为7.30×103kg/m3,熔化时的体积变化为+2.7%。
(分数:10.00)__________________________________________________________________________________________2.根据下列条件建立单元系相图:①组元A在固态有两种结构A1和A2,且密度A2>A1>液体;②A1转变到A2的温度随压力增加而降低;③A1相在低温是稳定相;④固体在其本身的蒸气压1333Pa(10mmHg)下的熔点是8.2℃;⑤在1.013×105Pa(1个大气压)下沸点是90℃;⑥A1,A2和液体在1.013×106Pa(10个大气压)下及40℃时三相共存(假设升温相变△H<0)。
(分数:10.00)__________________________________________________________________________________________3.考虑在1个大气压下液态铝的凝固,对于不同程度的过冷度,即△T=1,10,100和200℃,计算:①临界晶核尺寸;②半径为r*的晶核个数;③从液态转变到固态时,单位体积的自由能变化△G V;④从液态转变到固态时,临界尺寸r*处的自由能的变化△G r*(形核功)。
铝的熔点T m=993K,单位体积熔化热L m=1.836×109J/m3,固液界面比表面能δ=93×10-3J/m2,原子体积V0=1.66×10-29m3。