第6讲 平行线分线段成比例

3、如图梯形ABCD中点E、F分别在 AB、CD上EF∥AD假设EF作上下平 行移动
一、平行线分线段成比例定理： 三条平行线截两条直线所得的线段对应成比例. 关键要能熟练地找出对应线段
小结
二、要熟悉该定理的几种基本图形
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
a
（平行线分线段成 比例定理）。
三 练习
！
证明：因为
（平行线分线段成 比例定理）。
因为
已知：如图， ， 求证： 。
E
B
A
D
C
F
（平行线分线段 成比例定理）。
设AB=X则BC=8—X
即：
（平行线分线段成 比例定理）。
Excellent handout training template
平行线分线段成比例定理
l1
l2
l3
平行线分线段成比例定理： 三条平行线截两条直线所得的线段对应成比例 如图
已知l1∥l2∥l3 求证
或
或
定理的证明过A点作AN ∥ DF交l2于M交l3于N 点连接 BN 、CM如图1-2
∵l1∥l2∥l3 ∴AM =DE MN=EF 在△ACN中有
.
∵BM∥CN ∴S△BCN= S△BMN ∴
亦即
平行线分线段成比例定理： 三条平行线截两条直线所得的线段对应成比例
“对应”是数学的基本概念 图1-1中 在l1∥l2∥l3的条件下可分别推出如下结论之一： 1简称“上比下”等于“上比下” 2简称“上比全”等于“上比全” 3 简称“下比下”等于“下比下” 把这个定理运用于三角形中就得到它的重要推论

平行线分线段成比例教案
教案：平行线分线段成比例
教学目标：
1. 了解平行线的定义；
2. 掌握利用平行线分线段成比例的方法。

教学准备：
1. 板书：平行线的定义；
2. 构建平行线的示意图；
3. 一些练习题。

教学过程：
一、导入（5分钟）
1. 打开学生的思维，提问：你们知道什么是平行线吗？请举例说明。

2. 引导学生回答，然后板书平行线的定义。

二、讲解（10分钟）
1. 准备一个平行线的示意图，让学生观察图中的平行线，并请他们描
述平行线的性质。

2. 引导学生总结，平行线之间的性质是什么？
3. 说明平行线分线段成比例的方法：如果一条直线与两条平行线相交，那么这条直线所分割的平行线段与这两条平行线的相应线段成比例。

三、练习（25分钟）
1. 学生独立完成练习题。

2. 收作业并进行讲解。

四、拓展（5分钟）
1. 引导学生思考：如何应用平行线分线段成比例的方法解决生活中的
实际问题？
2. 引导学生举例说明，并进行讨论。

五、总结归纳（5分钟）
1. 总结平行线的定义和性质。

2. 总结平行线分线段成比例的方法。

六、作业布置（5分钟）
1. 布置练习题作业，要求学生运用平行线分线段成比例的方法解答问题。

教学反思：
通过上述教学过程，学生可以积极参与讨论，理解了平行线的定义和性质，并掌握了平行线分线段成比例的方法。

希望学生能够通过课后的练习巩固所学内容，并能运用到实际问题中。

《平行线分线段成比例》教案一、教学目标：知识与技能：1. 理解平行线分线段成比例的概念。

2. 学会使用直尺和圆规作图，证明平行线分线段成比例。

3. 能够运用平行线分线段成比例的性质解决实际问题。

过程与方法：1. 通过观察、操作、猜想、验证等活动，培养学生的空间想象能力和推理能力。

2. 学会与他人合作交流，发展学生的表达能力和概括能力。

情感态度价值观：1. 培养学生对数学的兴趣和自信心。

2. 培养学生勇于探究、积极思考的科学精神。

二、教学重点与难点：重点：1. 平行线分线段成比例的概念。

2. 平行线分线段成比例的证明方法。

难点：1. 理解平行线分线段成比例的内在联系。

2. 运用平行线分线段成比例解决实际问题。

三、教学方法：采用问题驱动法、案例分析法、合作交流法、实践操作法等。

四、教学准备：直尺、圆规、多媒体设备等。

五、教学过程：1. 导入新课：创设生活情境，展示两组直线平行时线段的比例关系，引发学生思考。

2. 自主探究：学生分组讨论，观察、操作、猜想、验证平行线分线段成比例的性质。

3. 合作交流：各小组汇报探究成果，师生共同总结平行线分线段成比例的证明方法。

4. 实践操作：学生运用所学知识，利用直尺和圆规作图，证明平行线分线段成比例。

5. 巩固提高：出示练习题，学生独立完成，检验对平行线分线段成比例的理解和掌握程度。

6. 总结反思：学生总结本节课所学内容，分享自己的收获和感悟。

7. 课后作业：布置相关作业，巩固所学知识，提高运用能力。

8. 教学反思：教师在课后对教学过程进行反思，总结成功经验和不足之处，为下一步教学做好准备。

六、教学评价：本节课结束后，将通过课堂表现、练习完成情况、课后作业和小组合作交流等方面对学生的学习情况进行评价。

重点关注学生对平行线分线段成比例概念的理解、证明方法的掌握以及实际应用能力的提升。

七、教学拓展：1. 让学生尝试证明其他图形中线段的比例关系。

2. 组织学生参观现实生活中的平行线分线段成比例的实例，如建筑物的布局、道路的设计等。

[证明] 作 EH∥AB 交 AC 于点 H， 则AAHC＝BBCE，∴ABCC＝ABHE. 同理：AAHF＝DDFE，∴DAFF＝ADHE. ∵△BDC 为直角三角形， 且 E 为 BC 边中点， ∴BE＝CE＝DE. ∴ABHE＝ADHE.∴ABCC＝DAFF.
证明比例式成立，往往会将比例式中各线段放到一组 平行线中进行研究．有时图形中没有平行线，要添加辅助 线，构造相关图形，创造可以形成比例式的条件，达到证 明的目的．
Hale Waihona Puke 5．如图，梯形 ABCD 中，AD∥BC，点 E，F 分别在 AB，CD 上，且 EF∥ BC，若AEEB＝23，AD＝8 cm，BC＝18 cm，求 EF 长．
解：作 AG∥DC 分别交 BC，EF 于 G，H， ∴AD＝HF＝GC＝8 cm. BG＝18－8＝10(cm)． ∵AEEB＝23，∴AAEB＝25. ∴EBHG＝AAEB＝25. ∴EH＝25×BG＝25×10＝4(cm)． ∴EF＝EH＋HF＝4＋8＝12(cm)．
平行线分线段成比例定理
1．平行线分线段成比例定理 (1)文字语言：三条平行线截两条直线，所得的对应线段成 比例．
(2)图形语言：
如图 l1∥l2∥l3， 则有：ABBC＝__DE_F_E__， AABC＝__DD_EF___，
EF BACC＝__D__F___.
变式有：DABE＝BECF，DABE＝DACF，BECF＝DACF.
则有：AADB＝__AA__EC__，ADDB＝___AE_EC__，DABB＝__CA__EC__.
3．平行线分线段成比例定理的作用 平行线分线段成比例定理及推论是研究下一节相似三角 形的理论基础，它可以判定线段成比例．另外，当不能直接 证明要证的比例成立时，常用该定理借助“中间比”转化成 另两条线段的比，来得出正确结论．合理添加平行线，运用 定理及推论列比例式，再经过线段间的转换可以求线段的比 值或证明线段间倍数关系．

l1 l2 l3
平行线分线段成比例定理： 三条平行线截两条直线所得的 线段对应成比例 如图
A
D
l1
已知l1∥l2∥l3 AB DE 求证 BC EF
或
或
AB DE AC DF
BC EF AC DF
B
E
l2
C
F
l3
定理的证明过A点作AN ∥ DF，交l2于M，交l3
于N 点，连接 BN 、CM（如图(1-2） ∵l1∥l2∥l3 ∴AM =DE MN=EF AB S ABM 在△ACN中，有
三
练习

l1 l2 l3


AB BC AC DE EF DF
！
上

下

全
已知：如图， l1 // l2 // l3 求AB。 A B C D E F
，AC=8，DE=2，EF=3， 方法一 解：因为 l1 // l2 // l3
l1
l2

AB DE （平行线分线段 BC EF 成比例定理）。
பைடு நூலகம்
例1 已知：如图 EF=4。求BC。
B C A D E F
l1 // l2 // l3 ，AB=3 ，DE=2 ，
l1 l2
l3
练习：已知：如图， l // l 1 2 EF=c. 求DE。
A B C D E F
// l3
，AB= a, BC= b,
l1 l2 l3
例 2 如图,△ABC中,DF//AC,DE//BC,AE=4,EC=2, BC=8.求BF和CF的长. 分析:运用平行线分线段成比例定理的推论分 A 别列出比例式求解. 解 ∵DE//BC
其实，世上最温暖的语言，“ 不是我爱你，而是在一起。” 所以懂得才是最美的相遇！只有彼此以诚相待，彼此尊重 ，相互包容，相互懂得，才能走的更远。 相遇是缘，相守是爱。缘是多么的妙不可言，而懂得又是多么的难能可贵。否则就会错过一时，错过一世！ 择一人深爱，陪一人到老。一路相扶相持，一路心手相牵，一路笑对风雨。在平凡的世界，不求爱的轰轰烈烈；不求誓 言多么美丽；唯愿简单的相处，真心地付出，平淡地相守，才不负最美的人生；不负善良的自己。 人海茫茫，不求人人都能刻骨铭心，但求对人对己问心无愧，无怨无悔足矣。大千世界，与万千人中遇见，只是相识的 开始，只有彼此真心付出，以心交心，以情换情，相知相惜，才能相伴美好的一生，一路同行。 然而，生活不仅是诗和远方，更要面对现实。如果曾经的拥有，不能天长地久，那么就要学会华丽地转身，学会忘记。 忘记该忘记的人，忘记该忘记的事儿，忘记苦乐年华的悲喜交集。 人有悲欢离合，月有阴晴圆缺。对于离开的人，不必折磨自己脆弱的生命，虚度了美好的朝夕；不必让心灵痛苦不堪， 弄丢了快乐的自己。擦汗眼泪，告诉自己，日子还得继续，谁都不是谁的唯一，相信最美的风景一直在路上。 人生，就是一场修行。你路过我，我忘记你；你有情，他无意。谁都希望在正确的时间遇见对的人，然而事与愿违时， 你越渴望的东西，也许越是无情无义地弃你而去。所以美好的愿望，就会像肥皂泡一样破灭，只能在错误的时间遇到错的人 。 岁月匆匆像一阵风，有多少故事留下感动。愿曾经的相遇，无论是锦上添花，还是追悔莫及；无论是青涩年华的懵懂赏 识，还是成长岁月无法躲避的经历……愿曾经的过往，依然如花芬芳四溢，永远无悔岁月赐予的美好相遇。 其实，人生之路的每一段相遇，都是一笔财富，尤其亲情、友情和爱情。在漫长的旅途上，他们都会丰富你的生命，使 你的生命更充实，更真实；丰盈你的内心，使你的内心更慈悲，更善良。所以生活的美好，缘于一颗善良的心，愿我们都能 善待自己和他人。 一路走来，愿相亲相爱的人，相濡以沫，同甘共苦，百年好合。愿有情有意的人，不离不弃，相惜相守，共度人生的每 一个朝夕……直到老得哪也去不了，依然是彼此手心里的宝，感恩一路有你！

平行线分线段成比例结论
平行线分线段成比例的结论可以用以下两个定理来描述：
1. 三角形法则：如果在两条平行线上有两个相交线段，那么这两条线段被平行线切分的部分成比例。

具体表述为：如果AB和CD是两条平行线，并且有两个交叉
线段EF和GH，那么EF/GH = AB/CD。

2. 价恩斯定理：两条平行线被一组相交线段切割所形成的任意两条线段之间的比值，等于这两条线段所在平行线之间的比值。

具体表述为：如果AB和CD是两条平行线，其中EF和GH
是这两条平行线上的两个交叉线段，那么EF/GH = AB/CD。

这些定理指出，在平行线上切割的线段之间存在比例关系，这使得我们可以通过已知线段的比例来推导未知线段的长度。

掌握情况
学生能够熟练掌握平行线分线段 成比例定理及其推论，能够运用 定理证明三角形相似，并了解相
似三角形的性质。
学习难点
部分学生在运用平行线分线段成 比例定理证明三角形相似时存在 困难，需要加强对定理的理解和
应用。
学习收获
通过学习，学生掌握了平行线分 线段成比例定理及其推论，提高 了证明三角形相似的能力，对相 似三角形的性质有了更深入的了
方法二
利用相似三角形的性质，通过计算得 到对应边之间的比例关系，从而判定 是否存在平行线。
实际问题中运用平行线分线
04
段成比例
实际问题背景介绍
01 建筑设计
在设计建筑时，需要利用平行线分线段成比例的 原理来确保建筑物的稳定性和美观性。
02 地理测绘
在地理测绘中，可以通过平行线分线段成比例的 方法来计算地图上的距离和面积。
利用面积证明
通过计算平行四边形的面积，利用面积法证明平行线分线段成比例定理。
定理应用举例
01 解决线段比例问题
利用平行线分线段成比例定理，可以解决一些涉 及线段比例的问题，如计算两条线段的比例、证 明两条线段成比例等。
02 解决角度问题
平行线分线段成比例定理也可以用于解决一些角 度问题，如证明两个角相等或互补等。
平行线分线段成比例 教学课件
目录
• 平行线与线段基本概念 • 平行线分线段成比例定理 • 相似三角形与平行线关系探讨 • 实际问题中运用平行线分线段成比
例 • 课堂互动环节 • 总结回顾与作业布置
01
平行线与线段基本概念
平行线定义及性质
01
平行线定义
在同一平面内，不相交的两条直线叫做平行线。
02

平行线段分线段成比例证明平行线段分线段成比例，这个听起来挺复杂的吧？咱们可以把它想象成一场友谊赛，参与者是两条平行线，还有一条小线段在中间起着分割的作用。

想象一下，两个好朋友在操场上玩耍，两个平行的线段就像这两个朋友，永远保持着同样的距离，绝不会走得太近，也不会远离彼此。

而那个小线段，就是他们之间的小桥梁，连接着这段友情。

这个道理特别简单。

就好比你跟朋友一起分享零食，你们每人分到的数量是一样的。

这时候，假设你们有两种零食，巧克力和薯片。

你把巧克力分给自己和朋友，结果每个人都有一份，而薯片也是如此。

这不就形成了一种比例吗？对了，平行线段之间的比例关系就像你们分享零食一样，永远保持着一致，谁都不会吃亏。

再想象一下，咱们画一条横线，把它放在两条平行线之间。

就像把一个巧克力棒横着放在两块巧克力之间，哈哈，想想就让人馋了。

这个横线就把两条平行线分成了几个小部分。

每个部分就像小朋友们分到的零食，分得公平，分得合理。

我们可以用简单的数学公式来表示这几个部分的关系，像是把一根长棍子折成几段，折得越整齐，比例就越好。

所以，当我们把这个概念再深入一点，可以发现，平行线段的比例关系不仅仅是数学题，它其实和我们生活中的很多事情都息息相关。

就像在一个团队里，大家分工合作，每个人的贡献都很重要。

如果某个人的工作量比另一个人多，那可能就不太公平了。

就像你吃巧克力的时候，朋友却只得到了几片薯片，这样的情况谁都不想看到，对吧？我们可以用一个简单的例子来说明这个原理。

假设我们有一条长长的公路，两旁都是平行的绿树。

你在公路中间跑步，想象一下，左边的树和右边的树永远保持着相同的距离。

然后，你在中间画一条线，标记一下你跑过的距离，结果你发现，无论你怎么跑，这两侧的树之间的距离始终都是一致的。

这就是平行线段分线段成比例的最佳体现，真的是让人感到神奇呢。

想想生活中那些有趣的事情吧！每当你看到平行线，就像看到朋友们齐心协力，分享快乐一样。

这种简单而又美好的关系，正是让我们的生活充满乐趣的源泉。

BE AE BF AF AB 1. BC AD BA AB AB
即 AE BE 1. AD BC
8.如图，在△ABC中，∠ACB＝90°，∠B＞∠A，点D为边AB的中 点，DE∥BC交AC于点E，CF∥BA交DE的延长线于点F.
求证：DE＝EF.
证明：∵DE∥BC，∴ AD AE .
DB EC ∵点D为AB 的中点，∴AD＝DB，即
归纳
平行于三角形一边的直线截其他两边(或两边的延长线)， 所得的对应线段成比例.
1.数学表达式：如图，
∵DE∥BC，
∴
AD AE ，AD AE ，BD＝ CE . DB EC AB AC AB AC
2.要点精析：
(1)本推论实质是平行线分线段成比例的基本事实中一组平行线中
的一条过三角形一顶点，一条在三角形一边上的一种特殊情况．
知识点 3 平行线分线段成比例的基本事实推论2
平行于三角形的一边，并且和其他两边相交的直线，所 截得的三角形与原三角形的对应边成比例．
例3 如图，在△ABC中，EF∥BC，
则
AF AC
和EF 分别是( A )
A. 1 ，3 3
B. 1 ，6 3
C. 1 ，9 2
D．无法确定
AE 1 ，BC＝9，
D. 2cm、3cm、4cm、6cm
2.两地实际距离是500 m，画在图上的距离是25 cm，若在此图上量得A、
B两地相距为40 cm，则A，B两地的实际距离是( A )
A. 800m
B. 8000m C. 32250cm
D. 3225m
3.如图，AD//BE//CF，直线l1、l2与这三条平行线分别交于点A、B、C和 点D、E、F.若AB=4.5，BC=3，EF=2，则DE的长度是( B )

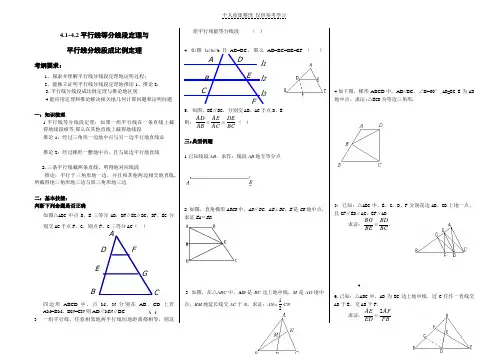
D BE F4.1-4.2平行线等分线段定理与 平行线分线段成比例定理考纲要求：1．探索并理解平行线分线段定理地证明过程；2．能独立证明平行线分线段定理地推论1、推论2； 3.平行线分线段成比例定理与推论地区别4.能应用定理和推论解决相关地几何计算问题和证明问题一：知识梳理1.平行线等分线段定理：如果一组平行线在一条直线上截得地线段相等,那么在其他直线上截得地线段推论1：经过三角形一边地中点与另一边平行地直线必推论2：经过梯形一腰地中点，且与底边平行地直线2.三条平行线截两条直线，所得地对应线段推论：平行于三角形地一边，并且和其他两边相交地直线.所截得地三角形地三边与原三角形地三边二：基本技能：判断下列命题是否正确如图△ABC 中点D 、E 三等分AB ，DF ∥EG ∥BC ，DF 、EG 分别交AC 于点F 、G ，则点F 、G 三等分AC （ ）四边形ABCD 中，点M 、N 分别在AB 、CD 上若AM=BM 、DN=CN 则AD ∥MN ∥BC ( )3. 一组平行线，任意相邻地两平行线间地距离都相等，则这组平行线能等分线段. （ ）4. 如图l 1//l 2//l 3且AB=BC ，那么AB=BC=DE=EF （ ）5．如图，DE ∥BC ，分别交AB 、AC 于点D 、E 则：BCDEAC AE AB AD ==（ ）三:典型例题1 已知线段AB ，求作：线段AB 地五等分点.2 如图，直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，E 是CD 地中点.求证EA ＝EB .4 3. 如图，在△ABC 中，AD 是BC 边上地中线，M 是AD 地中点，BM 地延长线交AC 于N ，求证：AN=21CN .4.如下图，梯形ABCD 中，AD//BC ，∠B=60°,AB=BC,E 为AB 地中点，求证:△ECD 为等边三角形.5：已知：△ABC 中，E 、G 、D 、F 分别是边AB 、CB 上地一点，且GF ∥ED ∥AC ，EF ∥AD求证：.BC BDBE BG =6.已知：△ABC 中，AD 为BC 边上地中线，过C 任作一直线交AD 于E ，交AB 于F.求证：FB AFED AE 2=A CGCB E D Fl 3l 2 l 1 A7：如图，已知：D 为BC 地中点，AG ∥BC ，求证：FCAFED EG =DCAG8．已知：△ABC 中，AD 平分∠BAC ， 求证：DCBDAC AB =（提示：过C 作CE ∥AD 交BA 地延长线于E ）9：△ABC 中，AD 平分∠BAC ，CM ⊥AD 交AD 于E ，交AB 于M ，求证：AMABDC BD =四：能力提升1.如图1所示，F 为AB 地中点，FG ∥BC ，EG ∥CD ，则AG ＝，AE ＝.2.如图2，直线l 过梯形ABCD 一腰AB 地中点E ，且平行于BC ，l 与BD ，AC 、CD 分别交于F 、G 、H ，那么，BF ＝，CG ＝，DH ＝.3.如图3，已知CE 是△ABC 地中线，CD=21AD,EF ∥BD ，EG ∥AC ，若EF=10cm ，则BG =cm ，若CD=5cm ，则AF=cm.4.已知：如图，B 在AC 上，D 在BE 上，且AB:BC=2:1，ED:DB=2:1求AD:DF5.△ABC 中，DE ∥BC ，F 是BC 上一点.AF 交DE 于点G ，AD:BD=2:1,BC=8.4cm 求(1)DE 地长(2)AFAG(3)ADE ABC S S ∆∆。

▪ . 已知：如图△ABC中，D、E分别是AB、AC上两 点，DE、BC旳延长线相交于F. AD=CF.
求证：BC = DE .
AB EF
措施一. 证明：作DM∥AC交BC于M.
在△ABC中， DM∥AC.
BC MC . AB AD
在△DMF中，
DE MC . EF CF
∵AD=CF，
BC DE . AB EF
A
D
E
B
C
问题处理4 P85
4如图，在△ABC中，D,E,F分别AB,AC,BC上 旳点，且DE∥BC,EF∥AB,AD:DB=2:3,
BC=20 cm
A
求BF旳长
E D
B F
C
课堂练习：
A 64 DE
9
B
C
EC＝（ ）
12
D
15
F 9 B
A
E
10
G C
AE＝（ ） GC＝（ ）
课堂练习：
已知：EG∥BC，GF∥CD
A
mE B
F C
例1：填空
A D
（1）∵ AB∥DE
B
E
C
∴
CD ＝（ CE） AC AD （ BE ） CD
＝（ BC ） BE （ CE ） BC
＝（ AD） （ AC）
（2）∵ AD∥EF ∥BC
A
D
∴
AG GC
＝（
（
AE） （ DF ） BE）＝ （ FC ）
E B
F G
C
（2）已知平行四边形ABCD
l4
l1
l2
l3
l5
l4
l1
l2
l3

一、教学目标1. 知识与技能：（1）理解平行线分线段成比例的概念。

（2）学会运用平行线分线段成比例定理解决实际问题。

2. 过程与方法：（1）通过观察、分析、归纳，培养学生直观想象能力。

（2）运用合作交流、探究发现的方法，提高学生解决问题能力。

3. 情感态度与价值观：培养学生对数学的兴趣，感受数学在生活中的应用，增强学生自信心。

二、教学重点与难点1. 教学重点：（1）平行线分线段成比例的概念。

（2）平行线分线段成比例定理的应用。

2. 教学难点：（1）平行线分线段成比例定理的推导过程。

（2）在实际问题中灵活运用平行线分线段成比例定理。

三、教学方法与手段1. 教学方法：（1）启发式教学：引导学生观察、分析、归纳平行线分线段成比例的规律。

（2）合作交流：分组讨论，培养学生团队协作能力。

（3）探究发现：引导学生自主探究，提高学生发现问题、解决问题的能力。

2. 教学手段：（1）多媒体课件：展示平行线分线段成比例的图形、实例。

（2）教具：使用模型、图纸等教具，增强学生直观感受。

四、教学过程1. 导入新课：（1）复习相关知识：回顾直线的性质、平行线的定义。

（2）提出问题：如何判断两条平行线是否分线段成比例？2. 自主探究：（1）学生分组讨论，观察、分析平行线分线段成比例的规律。

（2）汇报讨论成果，教师点评、指导。

3. 讲解与示范：（1）讲解平行线分线段成比例的概念。

（2）演示平行线分线段成比例定理的推导过程。

4. 练习与巩固：（1）发放练习题，让学生独立完成。

（2）讲解练习题，纠正错误，巩固知识点。

5. 应用拓展：（1）提出实际问题，让学生运用平行线分线段成比例定理解决。

五、课后作业（1）已知一组平行线分两个线段，其中一个线段长度为8cm，另一个线段长度为12cm，求这两条平行线之间的距离。

（2）一个长方形被一组平行线分成两个小长方形，长方形的长为10cm，宽为6cm，求这两个小长方形的面积。

六、教学评价1. 课堂表现评价：观察学生在课堂上的参与程度、提问回答、小组讨论等方面的表现，了解学生的学习状态。

平行线分线段成比例【把握要点，领会概念】㈠平行线分线段成比例定理：⑴定理: 两条直线被一组平行线所截，所得的对应线段___________.说明：①对应线段是指两条平行线所截的线段.②对应线段的比相等是指同一直线上的两条线段的比，等于另一条直线上与它们对应的线段的比.⑵推论: 平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段________.⑶平行于三角形一边并且和其他两边相交的________，所截得的三角形的三边与原三角形三边的对应线段成比例.⑷如果一条直线截三角形的两边(或两边的延长线),所得的对应线段_________,那么这条直线平行于三角形的第三边.注意：这四个定理主要提出由平行线可得到比例式；反之,有比例可得到平行线。

首先要弄清三个基本图形：★这三个基本图形的用途是:①由平行线产生比例式基本图形(1): 若l1//l2//l3，则或或或基本图形(2): 若DE//BC，则或或或基本图形(3): 若AC//BD，则或或或注意：在这里必须注意正确找出对应线段，不要弄错位置.②由比例式产生平行线段基本图形(2): 若, , , , , 之一成立，则DE//BC.基本图形(3): 若,,,,, 之一成立，则AC//DB. ③ 基本图形（1）有：两条直线被第三条平行线所截，如果在一条直线上截得的线段相等，那么在另一条 __________ 截得的线段也 _________. ㈡ 本讲内容所需要的计算与证明方法计算方法: 1.利用引入参数求解相关命题的方法. 2.会利用比例式建立方程求线段的长.证明方法: 会证比例式及等积式,会添加必要的辅助线求解相关命题. 【典型例题剖析】▲题型一：平行线分线段成比例概念及性质的应用例1.如右图，已知L 1//L 2//L 3，下列比例式中成立的是：（ ）A ．BC CE DF AD = B.AF BCBE AD = C. BC AD DF CE = D.CEBEDF AF = ★方法归纳：应用平行线分线段成比例定理得到的比例式中，四条线段与两条直线的交点位置无关，关键是线段的对应，可简记为：例2.（河北省）已知：如图，l 1∥l 2∥l 3，AB=3，BC=5，DF=12.求DE 和EF 的长.例3．如图，DE ∥AC ，EF ∥AB ，AC=14，AD ：DB=3：4，则AF 的长是（ ）A 6B 10C 8D 9A B L 1C D L 2E F L 3例4．如图，在梯形ABCD 中，AD ∥BC ，对角线AC ，BD 交于O ，过O 作底的平行线，分别与两腰交于E 、F ，则 （ ）A OE= OFB OE=OFC OE=2OF DOE+OF=BD例5.如图，DE BC ∥，且DB AE =,若510AB AC ==，，求AE 的长.例6.（2011•牡丹江）在△ABC 中，AB=6，AC=9，点D 在边AB 所在的直线上，且AD=2，过点D 作DE ∥BC 交边AC 所在直线于点E ，则CE 的长为__________ 例7．（2013•乌鲁木齐）如图，AB ∥GH ∥CD ，点H 在BC 上，AC 与BD 交于点G ，AB=2，CD=3，则GH 的长为 ___ ．例8．（2013•贵州）在平行四边形ABCD 中，E 在DC 上，若DE ：EC=1：2，则BF ：BE= _________ ．▲题型二：构造平行线证明成比例的线段 例1．在△ABC 中，AD 平分BAC ∠，求证：ACABDC BD =.ED CBA例2. 如图,在□ABCD 中，E 为AB 中点,，，EF 、AC 相交于G ，求 .例3 如图，D 是△ABC 的AB 边的中点，F 是BC 延长线上一点，连结DF 交AC 于E 点.求证: EA:EC=BF:CF例4 如图,菱形ABCD 内接于△AEF,AE=3,AF=5,求菱形ABCD 的边长.分析: 有平行线就能得到比例线段，求线段的长有时需要使用方程的思想方法来解决，本题给出了用比例式建立方程求线段长的一种常见方法，注意掌握解题的思路.例5. 如图，AB ∥GH ∥CD ，若AB=a ，CD=b ，GH=c ，求证：ba c 111+=.。

1 1
D B
E C
l2
A B C
l2
l3
l3
a A B
b D E L1 L2 F
C 平行线等分线段定理： 两条直线被三条平行线所 截，如果在一直线上所截 得的线段相等，那么在另 一直线上所截得的线段也 相等。
L3
AB BE = BC EF
平行线分线段成比例定理与平行线等分线段 定理有何联系？
A B D E
已知： 例1 已知：如图 EF=4。求BC。 。 。
A B C D E F
l1 // l2 // l3 ，AB=3 ，DE=2 ，
l1 l2
l3
练习：已知：如图， 练习：已知：如图， l // l // l ，AB= a, BC= b, 1 2 3 EF=c. 求DE。 。
A B C
D E F
l1 l2 l3
F
AD AE D AD AC 在∆ADC中∴EF//CD, , = AF AE B AB AD = AD AF
A
E C
∴AD2=AB•AF,即AD是AB和AF的比例中项
AB BC AC = = 已知：如图， 求证： 。 已知：如图，1 // l2 // l3 ， 求证： l DE EF DF 证明： 证明：因为 l1 // l2 // l3 AB DE （平行线分线段成 A D = 比例定理）。 BC EF 比例定理）。 AB BC B E = DE EF F C BC EF （平行线分线段成 因为 = 比例定理）。 AC DF 比例定理）。 BC AC = EF DF 上 下 全
三 练习
∴ ∴
l1 l2 l3
∴
∴
AB BC AC = = DE EF DF

教学目标：
（一）知识目标
1、理解并掌握平行线分线段成比例的基本事实及其推论。
2、能够利用平行线分线段成比例的基本事实及其推论解决相关问题。
（二）能力目标
通过应用，培养识图能力和推理论证能力，体会由特殊到一般的归纳推理的思想和方法。。
（三）情感与价值观目标
（1）、培养学生积极的思考、动手、观察的能力，使学生感悟几何知识在生活中的价值。
平行线分线段成比例说课稿
扫xx中学xx
一、学生知识状况分析
学生在本章前两课时的学习中，通过对相似图形的直观感知，体会到可以用对应线段长度的比来描述两个形状相同的平面图形的大小关系。从而认识了线段的比，成比例线段及其性质，并在探究活动中积累了一定的合作交流的经验，培养了提出问题与解决问题的能力。同时学生通过对合比性质与等比性质的演绎证明，也进一步发展了逻辑推理能力。
第二环节：
领学目标，明确学习任务；
让学生初步了解本节课要学什么知识，重难点分别是什么，做到心中有数。
第三环节：
小组合作，探究新知；
这一环节是本节课的重点和难的方式，让每位学生都能参与到平行线分线段成比例基本事实的归纳猜想中来，再通过符号语言和将对应线段形象的表示，加深理解便于学生掌握新知，同时突出重点突破难点。探究二是平行线分线段成比例基本事实的推论，学生在掌握了定理之后，对这一推论的掌握和符号表示显得轻而易举，在此归纳常见的基本图型，即“A”字型和“8”字型，对这一推论进行拓展延伸，提高学生的应用能力。探究三是对新知的应用和巩固。
第四环节：
课堂小结；
先留时间让学生归纳梳理本节课的知识点，在进行小组展示，提高学生的课堂参与意识和积极性。
第五环节：
课堂检测；要求学生独立完成，及时反馈学习效果。

A D B E F
l1 l2
l3
C
平行于三角形一边的直线截其他两边
平行线分线段成比例定理推论:
A D B E F
l1 l2
l3
C
平行于三角形一边的直线截其他两边
平行线分线段成比例定理推论:
AD B E F
l1 l2
l3
C
平行于三角形一边的直线截其他两边
平行线分线段成比例定理推论:
AD B E F
QR PQ 则 . KN HK
？
H
. .
K N P Q
.
R
l1 l2
. . .
练习2
已知：如图，l1∥l2∥l3， AB=3，DE=2， EF=4， 求BC.
A
D
l1
l2
B
3
2E 4 F
6 ?
C
l3
练习2
已知：如图，l1∥l2∥l3， AB=6，BC=2， EF=1， 求DE.
A 6 B 2 C
A
D
集中地分析这些比例式：
AB AC 上 全 是 ; DE DF 上 全 B
C
A
D E
l1 l2
F
l3
集中地分析这些比例式：
AB AC 上 全 是 ; DE DF 上 全 B BC AC 下 全 是 ;C EF DF 下 全
A
D E
l1 l2
F
l3
集中地分析这些比例式：
A B D E F
l1 l2
l3
C
平行线分线段成比例定理推论:
A B D E F
l1 l2
l3
C
平行线分线段成比例定理推论:

一、教学目标1. 知识与技能：（1）理解平行线分线段成比例的概念。

（2）学会运用平行线分线段成比例定理证明两条线段成比例。

（3）能够运用平行线分线段成比例定理解决实际问题。

2. 过程与方法：（1）通过观察、实验、猜想、验证等过程，发现平行线分线段成比例的规律。

（2）培养学生的逻辑思维能力和证明能力。

3. 情感、态度与价值观：（1）培养学生对数学的兴趣和好奇心。

（2）培养学生的团队合作精神。

二、教学重点与难点1. 教学重点：（1）平行线分线段成比例的概念。

（2）平行线分线段成比例定理的证明。

（3）平行线分线段成比例定理的应用。

2. 教学难点：（1）平行线分线段成比例定理的证明。

（2）解决实际问题时，如何运用平行线分线段成比例定理。

三、教学方法1. 情境创设：通过生活实例引入平行线分线段成比例的概念。

2. 自主探究：引导学生观察、实验、猜想、验证平行线分线段成比例的规律。

3. 小组合作：分组讨论，共同完成平行线分线段成比例定理的证明。

4. 案例分析：分析实际问题，引导学生运用平行线分线段成比例定理解决问题。

四、教学准备1. 教具：黑板、粉笔、多媒体设备。

2. 学具：直尺、三角板、笔记本。

五、教学过程1. 导入新课：（1）复习相关知识：回顾线段、射线、直线的基本概念。

（2）生活实例：展示两幅画面，一幅是铁路交叉处，另一幅是桥梁结构，引导学生观察并思考其中的平行线分线段成比例现象。

2. 自主探究：（1）引导学生观察教室内的直线、射线、线段，鼓励学生发现平行线分线段成比例的实例。

（2）学生分组实验，用量角器和直尺测量不同角度的平行线分线段，记录数据，分析规律。

3. 小组合作：（1）分组讨论，引导学生总结平行线分线段成比例的规律。

（2）每组派代表进行汇报，全班交流、总结。

4. 知识讲解：（1）讲解平行线分线段成比例的概念。

（2）引导学生理解平行线分线段成比例定理的证明过程。

5. 案例分析：（1）出示实际问题，引导学生运用平行线分线段成比例定理解决问题。