平行线分线段成比例及证明78079

平行线分线段成比例证明方法平行线分线段成比例是几何学中的重要概念之一，它在解决实际问题中有着广泛的应用。

本文将介绍一种基于平行线分线段成比例的证明方法。

一、问题描述假设有一条直线上的线段AB，平行于这条直线的另外两条直线分别与线段AB相交于点C和D。

我们需要证明线段AC与线段CB的比例等于线段AD与线段DB的比例，即AC/CB = AD/DB。

二、证明思路我们可以通过构造相似三角形来证明平行线分线段成比例的性质。

具体的证明方法如下：1. 过点C和D分别作线段AB的平行线，与直线上的另一条线段分别相交于点E和F。

2. 连接线段AE、AF、CF和CE，得到四边形AECF。

3. 由于平行线的性质，可以得知∠ACF = ∠CED，∠ACB = ∠CED。

4. 根据四边形内角和定理，四边形AECF的内角和为360度，因此∠ACF + ∠AFC + ∠CAF + ∠ACB = 360度。

5. 由于∠ACF = ∠ACB，可得∠AFC + ∠CAF = 180度。

6. 根据内角和为180度的三角形性质，可知三角形AFC和三角形CAF之间存在相似关系。

7. 由于相似三角形的对应边成比例，可以得知线段AC与线段CF 的比例等于线段AF与线段CA的比例，即AC/CF = AF/CA。

8. 同理，可以得知线段CB与线段CF的比例等于线段CE与线段CA的比例，即CB/CF = CE/CA。

9. 将上述两个等式相除，可得(AC/CF)/(CB/CF) = (AF/CA)/(CE/CA)，化简后得 AC/CB = AF/CE。

10. 由于线段AF与线段CE分别与线段AD和线段DB相等，可得AF/CE = AD/DB。

11. 综上所述，我们证明了线段AC与线段CB的比例等于线段AD 与线段DB的比例，即AC/CB = AD/DB。

三、实际应用平行线分线段成比例的性质在实际问题中有着广泛的应用。

例如，在建筑设计中，如果我们需要在一条直线上平分一段线段，可以通过构造平行线来实现这个目标。

平行线分线段成比例定理简介平行线分线段成比例定理（Parallelogram Proportion Theorem）是几何学中关于平行线与线段相交的一个重要定理。

该定理表明，如果在两条平行线上，有一条直线与这两条平行线相交，那么它所截取的线段与平行线的对应线段成比例。

定理描述设有两条平行线l和m，直线n与这两条平行线相交。

如果直线n依次截取了线段AB和CD，那么这两条线段的比例等于与AB和CD平行的线段的比例，即：AB/CD = AE/CF其中，A、B分别是直线n与l的交点，C、D分别是直线n与m的交点，E、F分别是直线n与l和m的另外两个交点。

证明过程为了证明平行线分线段成比例定理，我们可以使用类似于相似三角形的方法来进行证明。

步骤1：构造辅助线段首先，我们在直线n上任意取一点G，然后通过G分别作l和m的垂线GH和GK。

此时，我们得到了一个平行四边形AGHK。

通过平行线的性质，我们可以知道AG和HK是平行的，并且两条平行线之间的距离是相等的。

步骤2：证明三角形AFB与三角形CGD相似由于AGHK是一个平行四边形，所以我们可以得到以下结论：∠KGD = ∠HAG （对顶角）∠KDG = ∠GAH （对顶角）因此，根据AA相似性质，我们可以得出三角形AFB与三角形CGD相似。

步骤3：证明AE/CF = AB/CD在步骤2中，我们已经得到了三角形AFB与三角形CGD相似的结论。

根据相似三角形的基本性质，我们知道相似的三角形中，对应边的比例是相等的。

由于三角形AFB与三角形CGD相似，根据相似三角形的性质，我们可以得到以下比例等式：AB/CD = AF/CG而AF和CG分别是线段AE和线段CF在相似三角形中对应的边。

因此，我们可以得出以下结论：AB/CD = AE/CF步骤4：证明结论由于步骤3中得出的结论，我们证明了平行线分线段成比例定理。

应用举例平行线分线段成比例定理在解决几何问题中起着重要的作用。

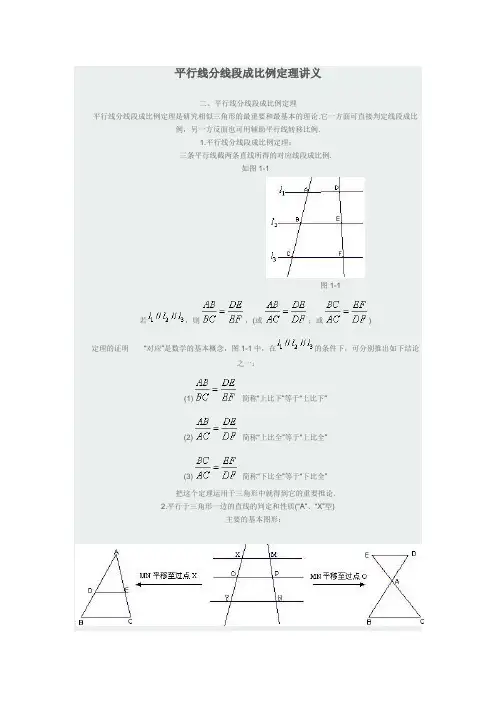
平行线分线段成比例定理讲义
二、平行线分线段成比例定理
平行线分线段成比例定理是研究相似三角形的最重要和最基本的理论.它一方面可直接判定线段成比
例，另一方反面也可用辅助平行线转移比例.
1.平行线分线段成比例定理：
三条平行线截两条直线所得的对应线段成比例.
如图1-1
图1-1
若，则，(或；或)
定理的证明“对应”是数学的基本概念，图1-1中，在的条件下，可分别推出如下结论
之一：
(1)简称“上比下”等于“上比下”
(2)简称“上比全”等于“上比全”
(3)简称“下比全”等于“下比全”
把这个定理运用于三角形中就得到它的重要推论.
2.平行于三角形一边的直线的判定和性质(“A”、“X”型)
主要的基本图形：
1．如图2-1 已知△ABC中AB=AC，AD⊥BC，M是AD的中点，CM交AB于P，DN∥CP
交AB于N，若AB=6cm，求AP的值.
点评：此题利用平行线分线段成比例定理，结合中点定义找出线段的比值，进而求出线段的长.
2．(如图2-2)已知直线截△ABC三边所在的直线分别于E、F、D三点且AD=BE.
求证：EF：FD=CA：CB.
图2-2又AD=BE
∴.
证法(二) 过E作EP∥BA交CA的延长线于P是解决此问题的第二种辅助线作法.
证法(三) 过D作DN∥BC交AB于N也可解决此问题.。

平行线分线段成比例定理引言在平面几何中，平行线分线段成比例定理是指当两条平行线与一条横截线相交时，它们所截取的线段之间的比例保持不变。

这个定理在很多几何证明和应用中都有重要的地位。

本文将介绍平行线分线段成比例定理的定义、证明以及应用，以及一些相关的例题。

定理描述设有两条平行线l1和l2，横截线AB与l1和l2相交于点C和D，若线段AC与线段DB所截取的部分成比例，即：AC/DB = AE/EB其中，E为AB的任意一点。

示意图示意图证明为了证明平行线分线段成比例定理，我们可以利用相似三角形的性质。

由于线段AC与线段DB所截取的部分成比例，可设AC = k • AE，DB = k • EB。

考虑△ACD和△EBD，根据平行线的定义，我们知道∠ACD = ∠EBD（对顶角）。

又因为∠CDA = ∠EDB（平行线与横截线交角），所以△ACD与△EBD相似。

根据相似三角形的性质，我们知道线段AC与线段DB的比例等于其余对应边的比例，即：AC/DB = AD/DE。

而根据比例的传递性，AD/DE = AE/EB。

综上所述，我们可以得到AC/DB = AE/EB，即平行线分线段成比例定理成立。

应用平行线分线段成比例定理在实际问题中有很多应用，以下是其中一些常见的应用场景：1. 三角形分线段在三角形中，如果有一条平行线与两边相交，根据平行线分线段成比例定理，我们可以利用已知的线段长度，求解未知的线段长度。

这在解题中经常用到。

2. 相似三角形在相似三角形中，如果有两条平行线各自与两个相似三角形的对应边相交，并且已知其中一个对应边的长度，根据平行线分线段成比例定理，我们可以求解另一个对应边的长度。

这对于解决相似三角形问题非常有用。

3. 求解比例问题平行线分线段成比例定理可以作为解决比例问题的一种工具。

当我们遇到线段的比例问题时，可以利用此定理来寻找线段之间的比例关系，从而求解未知线段的长度。

例题现给出一个例题来进一步理解平行线分线段成比例定理的应用：例题：在△ABC中，AD是BC的平分线，E是AB上的一点，DE与AC延长线交于F，若AB = 12cm，BC = 8cm，AD = 6cm，求EF的长度。

平行线分线段成比例定理的定理定义
在几何学中，平行线分线段成比例定理是关于平行线和线段的一个重要定理。

根据这个定理，当一条线段被两条平行线分割时，所得到的线段长度之比与其对应的平行线长度之比相等。

具体来说，我们假设有两条平行线l₁和l₂，它们分别与一条线段AB相交于点C和D。

根据平行线分线段成比例定理，我们可以得出以下结论：
如果AC:CB = AD:DB，那么线段AB被平行线l₁和l₂分割成的两个线段AC和CD的长度之比等于线段AB与平行线l₁和l₂的长度之比。

这个定理可以用于解决一些几何问题，例如计算线段的长度、证明一些图形的相似性等。

它在实际应用中也具有一定的重要性。

比如在工程测量中，我们可以利用平行线分线段成比例定理来计算难以直接测量的距离，从而提高测量的准确性。

总结一下，平行线分线段成比例定理是几何学中关于平行线和线段的重要定理。

它指出，当一条线段被两条平行线分割时，所得到的线段长度之比与其对应的平行线长度之比相等。

这个定理在几何问题的解决以及实际应用中有着重要的作用。

了解和掌握这个定理对于学习几何学和解决相关问题都是非常有帮助的。