当前位置：文档之家 › 第六章自相关案例分析

第六章自相关案例分析

  • 格式：doc
  • 大小：78.00 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

第六章 自相关(序列相关)

第六章 自相关(序列相关)

2 横截面数据中的自相关：一般来说截面数据不容
易出现自相关，但相邻的观测单位之间也可能存在 “溢出效应”（neighborhood effect）。例如，相邻 省份、国家之间的经济活动相互影响（通过贸易、 投资、劳动力流动等）；相邻地区的农业产量受到 类似的天气影响而相关；同一社区内的房屋价格存 在相关性；相邻地区的消费倾向有相关性
图 中 实 线 表 示 真 实 的 总 体 回 归 线 。 假 设 扰 动 项 存 在
正 自 相 关 ， 即 E ij X >0 ， 若 1>0 （ 图 中 左 边 小 椭 圆 形 ） 由 于 存 在 正 自 相 关 ， 则 2 >0 的 可 能 性 也 就 很 大 ； 而 若


n-1<0 （ 图 中 右 边 小 椭 圆 形 ） 则 n <0 的 可 能 性 也 就 很 大
此 检 验 被 称 为 B GB 检 验 （ r e u s c h － G o d f r e y ）
3B 、 o x P i e r c e Q 检 验
定义残差的各阶样本自相关系数为
t=j+1 ˆ j n
e e
t=1
n
t t－j
2 e t
（j＝1，2， ，p）
d ˆ 且 n 正 态 分 布 ， j ＝ 1 ， 2 ， ， p j
3 设 定 误 差 m i s s p e c i f i c a t i o n ： 如 果 模 型 设 定 中 遗 漏 会 引 起 扰 动 项 的 自 相 关 。
了 某 个 自 相 关 的 解 释 变 量 ， 并 被 纳 入 到 扰 动 项 中 ， 则
三 、 自 相 关 的 检 验
X X X X n 1 j ˆ ˆ Q ＝ S＋ 1 － etet-j xt x ＋ xt-jx t-j t n j＝ p+1 1i=j+1 p

计量经济学 第六章 自相关

计量经济学 第六章 自相关
5
计量经济学
第六章
自相关
6
一阶自相关系数
自相关系数 的定义与普通相关系的公式形式相同
n
utut-1
t=2
n
n
ut2
u2 t 1
t2
t2
的取值范围为 -1 1
(6.1)
式（6.1）中 ut-1是 ut 滞后一期的随机误差项。 因此，将式（6.1）计算的自相关系数 称为一阶 自相关系数。
模型中
ut
是
-1
ut
滞后一期的值，因此称为一阶。
此式中的 也称为一阶自相关系数。
18
如果式中的随机误差项 vt 不是经典误差项，即
其中包含有 ut 的成份，如包含有 ut2 则需将 vt
显含在回归模型中，其为
ut = 1ut-1 + 2ut-2 + vt
其中，1 为一阶自相关系数，2为二阶自相关系
另外回归模型中的解释变量在不同时期通常是
正相关的，对于
Xt和
X
t
来说
j
Xt Xt+j 是大于0的。
33
因此，普通最小二乘法的方差 Var(ˆ2) = 2 Σxt2
通常会低估 ˆ2 的真实方差。当 较大和 Xt 有
较强的正自相关时，普通最小二乘估计量的方 差会有很大偏差，这会夸大估计量的估计精度， 即得到较小的标准误。 因此在有自相关时，普通最小二乘估计 ˆ2 的标 准误就不可靠了。
许多农产品的供给呈现为 蛛网现象，供给对价格的 反应要滞后一段时间，因 为供给需要经过一定的时
间才能实现。如果时期 t
的价格 Pt 低于上一期的 价格 Pt-1 ，农民就会减少 时期 t 1 的生产量。如

第6章 自相关

第6章 自相关

2、序列相关性的后果 、
计量经济学模型一旦出现序列相关性，如果仍 采用OLS法估计模型参数，会产生下列不良后果：
(1)参数估计量非有效 (1)参数估计量非有效
因为，在有效性证明中利用了 E(UU’)=σ2I 即同方差性和互相独立性条件 同方差性和互相独立性条件。 同方差性和互相独立性条件 而且，在大样本情况下，参数估计量虽然具有 参数估计量虽然具有 一致性，但仍然不具有渐近有效性。 一致性，但仍然不具有渐近有效性。
例如，绝对收入假设 居民总消费函数模型 居民总消费函数模型： 例如，绝对收入假设下居民总消费函数模型 Ct=β0+β1Yt+µt t=1,2,…,n
由于消费习惯 消费习惯的影响被包含在随机误差项中， 消费习惯 则可能出现序列相关性（往往是正相关 ）。
• (3) 回归模型中略去了带有自相关的重要解释变量。 回归模型中略去了带有自相关的重要解释变量。 • 若丢掉了应该列入模型的带有自相关的重要解 释变量，那么它的影响必然归并到误差项ut中 释变量，那么它的影响必然归并到误差项 中，从 而使误差项呈现自相关。 而使误差项呈现自相关。当然略去多个带有自相关 的解释变量， 的解释变量，也许因互相抵消并不使误差项呈现自 相关。 相关。
6.2 自相关的来源和后果
1、自相关的来源 、 1)模型设定的偏误 (1)模型设定的偏误 所谓模型设定偏误 设定偏误（Specification error）是指 设定偏误 所设定的模型“不正确”。主要表现在模型中丢掉 了重要的解释变量或模型函数形式有偏误。 例如，本来应该估计的模型为 例如 Yt=β0+β1X1t+ β2X2t + β3X3t + µt
Yi=β0+β1X1i+…βkXki+γYi-1+µi β β …β γ µ

计量经济学第六章自相关

计量经济学第六章自相关

计量经济学第六章自相关自相关是计量经济学中一种重要的现象，它指的是一个变量与其自己在过去时间点上的相关性。

自相关在实证研究中十分常见，对经济学家来说，了解和掌握自相关性质是至关重要的。

1. 引言自相关作为计量经济学的一项基础概念，是经济学研究中不可或缺的一个重要方法。

自相关性的存在通常会引起回归结果的偏误，而忽略自相关性可能导致估计不准确的结果。

因此，探讨自相关性的性质和应对方法是计量经济学的重点之一。

2. 自相关的定义和表示自相关是指一个变量与其自身在过去时间点上的相关性。

假设我们有一个时间序列数据集，其中变量yt表示一个时间点上的观测值，t表示时间索引。

自相关系数可以通过计算观测值yt与其在过去某一时间点上的观测值yt-k（k为时间滞后期数）的相关性来得到。

数学上，自相关系数可以用公式表示为：ρ(k) = Cov(yt, yt-k) / (σ(yt) * σ(yt-k))其中，ρ(k)表示第k期的自相关系数，Cov表示协方差，σ表示标准差。

3. 自相关性的性质自相关性具有以下几个性质：3.1 一阶自相关性一阶自相关性是指变量值yt与前一期的观测值yt-1之间的相关性。

一阶自相关系数ρ(1)通常用来检验时间序列数据是否存在自相关性。

若ρ(1)大于零且显著，则表明存在正的一阶自相关性；若ρ(1)小于零且显著，则表明存在负的一阶自相关性。

3.2 高阶自相关性除了一阶自相关性，时间序列数据还可能存在高阶自相关性。

高阶自相关性是指变量值yt与过去第k期的观测值yt-k之间的相关性。

通过计算不同滞后期的自相关系数ρ(k)，可以了解数据在不同时间跨度上的自相关性情况。

3.3 异方差自相关性异方差自相关性是指时间序列数据中的方差不仅与自身相关，还与过去观测值的相关性有关。

异方差自相关性可能导致在回归分析中的标准误差失效，从而产生无效的回归结果。

因此，在处理存在异方差自相关性的数据时要采取合适的修正方法。

4. 自相关性的检验方法在实证研究中，经济学家通常使用多种方法来检验数据中的自相关性，常用的方法包括：4.1 Durbin-Watson检验Durbin-Watson检验是一种常用的检验自相关性的方法，其基本思想是通过检验误差项的相关性来判断自相关是否存在。

第六章自相关案例分析

第六章自相关案例分析

第六章 案例分析一、研究目的2003年中国农村人口占59.47％，而消费总量却只占41.4%，农村居民的收入和消费是一个值得研究的问题。

消费模型是研究居民消费行为的常用工具。

通过中国农村居民消费模型的分析可判断农村居民的边际消费倾向，这是宏观经济分析的重要参数。

同时，农村居民消费模型也能用于农村居民消费水平的预测。

二、模型设定正如第二章所讲述的，影响居民消费的因素很多，但由于受各种条件的限制，通常只引入居民收入一个变量做解释变量，即消费模型设定为t t t u X Y ++=21ββ（6.43）式中，Y t 为农村居民人均消费支出，X t 为农村人均居民纯收入，u t 为随机误差项。

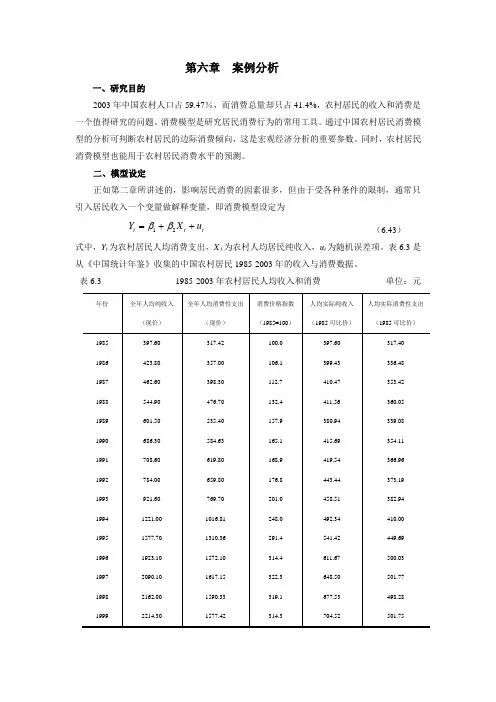
表6.3是从《中国统计年鉴》收集的中国农村居民1985-2003年的收入与消费数据。

表6.3 1985-2003年农村居民人均收入和消费 单位： 元2000 2001 2002 20032253.40 2366.40 2475.60 2622.241670.00 1741.00 1834.00 1943.30314.0 316.5 315.2 320.2717.64 747.68 785.41 818.86531.85 550.08 581.85 606.81注：资料来源于《中国统计年鉴》1986-2004。

为了消除价格变动因素对农村居民收入和消费支出的影响，不宜直接采用现价人均纯收入和现价人均消费支出的数据，而需要用经消费价格指数进行调整后的1985年可比价格计的人均纯收入和人均消费支出的数据作回归分析。

根据表6.3中调整后的1985年可比价格计的人均纯收入和人均消费支出的数据，使用普通最小二乘法估计消费模型得t t X Y 0.59987528.106ˆ+=（6.44）Se = (12.2238) (0.0214)t = (8.7332)(28.3067)R 2 = 0.9788，F = 786.0548，d f = 17，DW = 0.7706该回归方程可决系数较高，回归系数均显著。

南开大学计量经济学第6章自相关

南开大学计量经济学第6章自相关

经济模型中最常见的是一阶自回归形式。
T
ut ut1
依据 OLS 公式，模型 ut = 1 ut -1 + vt 中1 的估计公式是
aˆ1
=
t=2 T
。
ut12
t=2
若把 ut, u t-1 看作两个变量，则它们的相关系数是 ˆ =
T
ut ut1
t=2
。
T
T
ut 2
u t 1 2
（2）样本容量T
21 1.22 1.42 1.13 1.54 1.03 1.67 0.93 1.81 0.83 1.96
22 1.24 1.43 1.15 1.54 1.05 1.66 0.96 1.80 0.86 1.94 （3）原回归模型中解 23 1.26 1.44 1.17 1.54 1.08 1.66 0.99 1.79 0.90 1.92 释变量个数k（不包括
《Econometrics》 《计量经济学》
攸频
nkeconometrics126 南开大学经济学院数量经济研究所
第六章 自相关
Autocorrelation
§6.1 基本概念、类型及来源 §6.2 自相关的后果 §6.3 自相关的检验（DW检验、LM检验） §6.4 自相关的修正（GLS） §6.5 案例
同理，Cov(ut, ut - s) = s Var(ut)
自相关的表现形式
§6.1.3 自相关的来源
（1）惯性 大多数经济时间数据都有一个明显的特点，即
具有惯性。 如：经济周期
棘轮效应
（2）设定偏误：模型中遗漏了显著的变量
例如：如果对羊肉需求的正确模型应为
Yt=b0+b1X1t+b2X2t+b3X3t+ut

6.1自相关的概念及产生原因

6.1自相关的概念及产生原因

0时，称ut 不存在自相关。
ut为一阶自回归形式时的特点：
(1) E (ut ) 0
v2 2 (2)Var(ut ) u 常数 2 1
2 (3)Cov(ut , ut s ) s u (s 0)
可见，当随机误差项满足一阶自回归形式的自 相关时，随机误差项满足零均值和同方差的假定， 但不满足无自相关的假定。
则称模型存在自相关性。
二、自相关的分类
自相关按形式可分为两类：
（1）一阶自回归形式
当随机误差项ut 只与其滞后一期值ut 1有关时，即
ut f (ut 1 ) vt
称ut 具有一阶自回归形式。
（2）高阶自回归形式
当随机误差项ut 不仅与其前一期值有关，而且与其 前若干期的值都有关时，即
注意：时间序列数据比横截面数据更容易产生自相关。
3.模型设定不当的影响 例如，平均成本函数应该是二次多项式模型， 如果设成了线性模型，则随机误差项是自相关的。 因为这时随机误差项包括了产量的平方项，产量的 各期相关性将会导致随机误差项的自相关性。 4.一些随机干扰因素的影响 例如，自然灾害、金融危机等随机因素的影响， 往往要持续多个时期。从而使得随机误差项呈现出 自相关性。
ut f (ut 1，ut 2， ) vt
称ut 具有高阶自回归形式。
计量经济模型中自相关的最常见的形式是一 阶线性自回归形式
ut ut 1 vt
其中， 是ut 与ut 1的相关系数，vt 是满足基本假定的 随机误差项。的取值范围是[-1， 1]。当 0时，称 ut 存在正自相关，当 01.模型中遗漏了重要的解释变量
例如，以年度资料建立居民消费函数时，居民 消费除了受收入水平影响之外，还受消费习惯、 家庭财产等因素的影响，这些因素的各期值一般 是相关的，如果模型中未包含这些因素，它们对 消费的影响就表现在随机误差项中，从而使随机 误差项的各期值之间呈现出相关关系。

自相关

自相关
(3) 原回归模型中解释变量个数k（不包括常数项）。
6.3 自相关检验
（3）LM检验（亦称BG检验）法
（第2版169页） （第3版145页）
LM 统计量既可检验一阶自相关，也可检验高阶自相关。
LM 检验是通过一个辅助回归式完成的，具体步骤如下。
Yt = 0 + 1 X1 t + 2 X2 t + … + k Xk t + ut 考虑误差项为 n 阶自回归形式 ut = 1 ut-1 + … + n ut - n + vt H0: 1 = 2 = …= n = 0
T
T
ut 2
u
t
2 1
t2
t2
t2
t2
把这种关系代入上式得
T
ut ut1
ˆ t2
T
aˆ1
u
t
2 1
t2
对于总体参数有 = a1，回归模型中误差项 ut 的
一阶自回归形式可表示为， ut = ut-1 版教材第136页）
ˆ = 1 -（DW / 2）
2. 直接拟合估计。
6.6 案例分析
（第2版177页） （第3版152页）
例6.1 天津市城镇居民人均消费与人均可支配收入的关系。
改革开放以来，天津市城镇居民人均消费性支出（CONSUM），人 均可支配收入（INCOME）以及消费价格定基指数（PRICE）数据 （1978~2000年）见表6.2。现在研究人均消费与人均可支配收入的关系。
怎样查明自相关是由于略去重要解释变量引起的？一种方法 是用残差et对那些可能影响被解释变量，但又未单列入模型的 解释变量回归，并作显著性检验。
只有当以上两种引起自相关的原因都排除后，才能认为误差 项ut 真正存在自相关。

第06章 自相关(讲稿)

第06章 自相关(讲稿)

第6章自相关1. 自相关定义1）非自相关由第2节知回归模型的假定条件之一是，Cov(u i,u j )=E(u i u j) =0, (i, j∈T, i ≠ j),(1.1)即误差项u t的取值在时间上是相互无关的。

称误差项u t非自相关。

2）自相关如果Cov (u i ,u j ) ≠ 0, (i ≠ j)则称误差项u t存在自相关。

自相关又称序列相关。

原指一随机变量在时间上与其滞后项之间的相关。

这里主要是指回归模型中随机误差项u t 与其滞后项的相关关系。

自相关也是相关关系的一种。

2．自相关类型1）自相关按滞后阶数可分为两类。

(1)一阶自回归形式当误差项u t只与其滞后一期值有关时，即u t = f (u t - 1),称u t具有一阶自回归形式。

(2) 高阶自回归形式当误差项u t的本期值不仅与其前一期值有关，而且与其前若干期的值都有关系时，即u t = f (u t – 1, u t – 2 , … ), 则称u t 具有高阶自回归形式。

2）按函数形式分为线性自相关和非线性自相关 （1）线性自相关 f 为线性函数形式 （2）非线性自相关 f 为非线性函数形式 3．一阶线性自相关通常假定误差项的自相关是线性的。

因计量经济模型中自相关的最常见形式是一阶自回归形式，所以下面重点讨论误差项的线性一阶自回归形式，即 u t =1a u t -1 + v t (1.2)其中1a 是自回归系数，v t 是随机误差项。

v t 满足通常假设E(v t ) = 0, t = 1, 2 …, T, Var(v t ) = σv 2, t = 1, 2 …, T,Cov(v i , v j ) = 0, i ≠ j, i, j = 1, 2 …, T, Cov(u t-1, v t ) = 0, t = 1, 2 …, T,依据普通最小二乘法公式，模型（1.2）中 1 的估计公式是，1ˆa= ∑∑=-=-Tt t Tt t tuuu 22121 (1ˆβ=∑∑---2)())((x x x x y y t t t ) (1.3)其中T 是样本容量。

计量经济学 第六章 自相关

计量经济学 第六章 自相关

5
3、模型设定不当
(1)数学模型设定不当 比如我们在非线性回归模型中介绍的产品总成本Y和产量X 的回归模型为:
Yt b0 b1 X t b2 X b3 X t
2 t 3 t
但如果用线性模型来替代
Yt b0 b1 X t t
2 3
那么随机误差项
vt b2 X t b3 X t t
若d 0.562, 则0 d d L , 存在一阶正自相关
若d 3.521, 则4 d L d 4, 存在一阶负自相关
若d 2, 则dU d 4 dU , 不存在一阶自相关 若d 1.267, 则d L d dU , 无法确定模型中是否存在一阶自相关 若d 2.980, 则4 dU d 4 d L , 无法确定模型中是否存在一阶自相关
无自相关 区域
负自相关区域 正自相 关区域
0
dL
dU
2
4 dU
4 dL 4
17
例题6.1
在给定的显著性水平＝0.05条件下，n 10, k 1
查表得下限值d L 0.879, 上限值dU 1.320 又可以计算得4 dU 2.68, 上限值4 d L 3.121
2 2
若nR ( p ), 拒绝原假设，原模型存在自相关
2 2
若nR ( p), 接受原假设，原模型不存在自相关
2 2
拒绝域
接受域
( p )
2
nR
2
( p )
2
nR
2
22
6.4 自相关的修正
• 自相关修正的基本原理：通过差分变换，对原始数据进行 修正。自相关修正主要有三种方法。 • 1、广义差分法

计量经济学案例分析报告

计量经济学案例分析报告

《计量经济学》实验报告实验课题：各章节案列分析姓名：茆汉成班级：会计学12-2班学号：指导老师：蒋翠侠报告日期：目录第二章简单线性回归模型案例 (1)1 问题引入 (2)2 模型设定 (2)3 估计参数 (2)4 模型检验 (2)第三章多元线性回归模型案例 (3)1 问题引入 (3)2 模型设定 (3)3 估计参数 (4)4 模型检验 (4)第四章多重线性案例 (4)1 问题引入 (4)2 模型设定 (5)3 参数估计 (5)4 对多重共线性的处理 (5)第五章异方差性案例 (6)1 问题引入 (6)2 模型设定 (6)3 参数估计 (6)4 异方差检验 (7)5 异方差性的修正 (7)第六章自相关案例 (8)1 问题引入 (8)2 模型设定 (8)3 用OLS估计 (8)4 自相关其他检验 (8)5 消除自相关 (9)第七章分布滞后模型与自回归模型案例 (9)案例1 (9)1 问题引入 (9)2 模型设定 (10)3 参数估计 (10)案例2 (10)1 问题引入 (10)2 模型设定 (10)3、回归分析 (10)4 模型检验 (11)第八章虚拟变量回归案例 (11)1 问题引入 (11)2 模型设定 (11)3 参数估计 (12)4 模型检验 (12)第二章简单线性回归模型案例1、问题引入居民消费在社会经济的持续发展中有着重要的作用。

适度的居民消费规模和合理的消费模型是人民生活水平的具体体现，有利于经济持续健康的增长。

随着社会信息化程度和居民的收入水平的提高，计算机的运用越来越普及，作为居民耐用消费品重要代表的计算机已经为众多的城镇居民家庭所拥有。

研究中国各地区城镇居民计算机拥有量与居民收入水平的数量关系。

影响居民计算机拥有量的因素有多种，但从理论和经验分析，最主要的影响因素应是居民收入水平。

从理论上说居民收入水平越高，居民计算机拥有量越多。

所以我们设定“城镇居民家庭平均每百户计算机拥有量（台）”为被解释变量，“城镇居民平均每人全年家庭总收入（元）”为解释变量。

计量经济学第六章自相关

计量经济学第六章自相关

计量经济学第六章自相关在计量经济学的学习中，自相关是一个重要且颇具挑战性的概念。

自相关，简单来说，就是指在时间序列或横截面数据中，观测值之间存在的某种相关性。

想象一下，我们在研究某个经济变量随时间的变化情况，比如一家公司的销售额。

如果在不同的时间段，销售额的变化不是相互独立的，而是存在一定的关联，这就可能出现了自相关现象。

自相关产生的原因多种多样。

其中一个常见的原因是经济变量的惯性。

例如，消费者的消费习惯往往具有一定的延续性，不会突然发生巨大的改变。

这就导致消费数据在不同时期可能存在相关性。

另一个可能的原因是模型设定的不准确。

如果我们在构建计量经济模型时，遗漏了某些重要的解释变量，那么残差项就可能包含这些被遗漏变量的影响，从而导致自相关。

自相关的存在会给我们的计量经济分析带来一系列问题。

首先，它会影响参数估计的有效性。

在存在自相关的情况下，传统的最小二乘法（OLS）估计得到的参数估计值不再是最优的，估计的方差也会被低估，这可能导致我们对参数的显著性做出错误的判断。

其次，自相关会使我们对模型的假设检验失效。

假设检验是基于一定的统计分布进行的，如果存在自相关，这些分布就不再适用，从而导致检验结果的不可靠。

那么，如何检测自相关呢？常用的方法有图形法、杜宾瓦特森（DurbinWatson）检验等。

图形法是通过绘制残差的序列图来直观地观察是否存在自相关。

如果残差呈现出某种周期性或趋势性，那么就可能存在自相关。

杜宾瓦特森检验则是一种基于统计量的检验方法。

它通过计算一个特定的统计量，并与临界值进行比较来判断是否存在自相关。

如果经过检测发现存在自相关，我们就需要采取相应的方法来处理。

一种常见的方法是广义最小二乘法（GLS）。

GLS通过对原模型进行变换，使得变换后的模型不存在自相关，从而得到更有效的参数估计。

另外，还可以使用一阶差分法。

这种方法将原变量的一阶差分作为新的变量进行回归分析，从而消除可能存在的自相关。

第六章 自相关(序列相关)

第六章 自相关(序列相关)

2 横截面数据中的自相关：一般来说截面数据不容
易出现自相关，但相邻的观测单位之间也可能存在 “溢出效应”（neighborhood effect）。例如，相邻 省份、国家之间的经济活动相互影响（通过贸易、 投资、劳动力流动等）；相邻地区的农业产量受到 类似的天气影响而相关；同一社区内的房屋价格存 在相关性；相邻地区的消费倾向有相关性
第六章 自相关（序列相关）
一 、 自 相 关 的 后 果 违 反 球 型 扰 动 项 假 定 的 另 一 情 形 是 自 相 关 。 若 存 在 i j使 得 E ， 即 扰 动 项 的 协 方 差 阵 V a r X i j X 0 的 非 主 对 角 线 元 素 不 全 为， 0 则 称 存 在 “ 自 相 关 ” （ a u to c o rre la tio n ） 或 “ 序 列 相 关 ” （ se ria lc o rre la tio n ）
3 设 定 误 差 m i s s p e c i f i c a t i o n ： 如 果 模 型 设 定 中 遗 漏 会 引 起 扰 动 项 的 自 相 关 。
了 某 个 自 相 关 的 解 释 变 量 ， 并 被 纳 入 到 扰 动 项 中 ， 则
三 、 自 相 关 的 检 验
大 样 本 下 是 等 价 的 ， 但 L ju n g － B o x Q统 计 量 的 小 样 本 性 质 更 好 。
自 相 关 阶 数 p 如 何 给 出 ？ 可 由 统 计 软 件 默 认 给 定 。 助 回 归 的 参 数 的 显 著 性 检 验 来 判 断 自 相 关 的 阶 数
也 可 以 从 1 阶 、 2 阶 逐 次 向 更 高 阶 检 验 ， 借 助 辅
为 何 要 引 入 解 释 变 量， x ，呢 x t 1 t k ？

计量经济学课件：第六章-自相关性

计量经济学课件：第六章-自相关性

第六章 自相关性本章教学要求：本章是违背古典假定情况下线性回归描写的参数估计的又一问题。

通过本章的学习应达到：掌握自相关的基本概念，产生自相关的背景；自相关出现对模型影响的后果；诊断自相关存在的方法和修正自相关的方法。

能够运用本章的知识独立解决模型中的自相关问题。

经过第四、五、六章的学习，要求自行选择一个实际经济问题，建立模型，并判断和解决上述可能存在的问题。

第一节 自相关性的概念一、一个例子研究中国城镇居民消费函数，其中选取了两个变量，城镇家庭商品性支出（现价）和城镇家庭可支配收入（现价），分别记为CSJTZC 和CSJTSR ，时间从1978年到1997年，n=20。

但为了剔除物价的影响，分别对CSJTZC 和CSJTSR 除以物价（用CPI 表示），这里CPI 为城镇居民消费物价指数（以1990年为100%），经过扣除价格因素以后，记CPICSJTSRX CPICSJTZCY ==即如下表回归以后得到的残差为Dependent Variable: YMethod: Least SquaresDate: 10/27/04 Time: 09:39Sample: 1978 1997Included observations: 20Std. Error t-Statistic Prob.Variable CoefficientC-103.369278.80739-1.3116690.2061X0.9235510.01603357.603880.00003939.341 R-squared0.994605Mean dependentvarAdjusted R-squared0.994305S.D. dependent var2124.467S.E. of regression160.3247Akaike info criterion13.08692Sum squared resid462671.9Schwarz criterion13.18649Log likelihood -128.8692 F-statistic 3318.207 Durbin-Watson stat1.208037 Prob(F-statistic)0.000000二、什么是自相关性在引出自相关性的概念之前，根据建立中国城镇居民储蓄函数，经用最小二乘法估计出参数后，得到残差序列，由此画出残差图（残差序列自身的关系），从图形上看存在t e 对1 t e 的线性关系，残差的这种现象说明了什么？下面给出序列自相关的定义。

计量经济学(第六章自相关)

计量经济学(第六章自相关)
即得到较小旳原则误。
所以在有自有关时，一般最小二乘估计 ˆ2 旳原 则误就不可靠了。
Econometrics 2003
20
一种被低估了旳原则误意味着一种较大旳t统计
量。所以，当 0时，一般t统计量都很大。
这种有偏旳t统计量不能用来判断回归系数旳明 显性。 综上所述，在自有关情形下，不论考虑自有关， 还是忽视自有关，一般旳回归系统明显性旳t检 验都将是无效旳。 类似地,因为自有关旳存在,参数旳最小二乘估 计量是无效旳，使得F检验和t检验不再可靠。
cov(i , j ) E(i j ) 0存在i j
常见于时间序列数据。
Econometrics 2003
3
自有关类型：一阶自有关
一阶自相关：Cov(ut , ut1) 0;
若进一步，有ut＝ut1＋t ,
则称ut一阶线性自相关
（其中 |
|
1，
为白噪声序列，
t
即E(t ) 0, Cov(t , s ) 0(t s),
作为散布点绘图，假如大部分点落在第Ⅰ、Ⅲ象限，表白
随机误差项 ut 存在着正自有关。
Econometrics 2003
25
et
et
et-1et 1
图 6.2 et与et-1旳关系
假如大部分点落在第Ⅱ、Ⅳ象限，那么随机误
差项 ut 存在着负自有关。
Econometrics 2003
26
et
t
二、对模型检验旳影响
Econometrics 2003
30
n
n
n
et2 +
e2 t -1
-
2
et et -1
DW = t=2
t=2 n

自相关案例分析

自相关案例分析
计算自相关函数
自相关案例分析
自相关案例分析
接下来，我们需要计算自相关函数。自相关 函数的计算方法是，对于不同的时间延迟( 或滞后)值，计算当前回报率与未来回报率 之间的相关性。具体来说，对于每个时间延 迟值，我们可以将数据分成两部分，一部分 是前一部分的数据，一部分是后一部分的数 据。然后我们计算前一部分数据的回报率与 后一部分数据的回报率之间的相关性
NEXT
自相关案例分析
最后，我们可以通过比较不同时 间范围内的自相关函数图像来分 析回报率的自相关性。例如，我 们可以分别计算短期、中期和长 期时间范围内的自相关函数，并 比较它们的结果。这有助于我们 了解股票市场在不同时间范围内 的自相关性特征
总结
自相关案例分析
通过这个案例分析，我们了 解了自相关的概念和如何使 用自相关函数来衡量时间序 列数据的自相关性。我们发 现股票市场的回报率存在自 相关性，这种自相关性随着 时间延迟值的增加而逐渐减 弱。通过进一步分析自相关 函数的结果，我们可以了解 股票市场回报率的时域特征， 为投资决策提供有价值的参
自相关案例分析
自相关案例分析
目录
自相关案例分析
自相关是统计学中一个重要的概念，它描述 的是时间序列数据自身的依赖性。自相关函 数(ACF)是衡量时间序列数据自相关性的工 具。下面我们将通过一个具体的案例来分析 自相关
案例背景：假设我们有一个关于某股票市 场的日交易数据，我们想要研究这个股票 市场的自相关性。具体来说，我们想要通 过自相关函数来分析这个股票市场今天的 回报率与明天的回报率之间的关系
分析自相关函数的结果
自相关案例分析
通过观察自相关函数的图形，我 们可以看到当前回报率与未来回 报率之间的相关性随着时间延迟 值的增加而逐渐减弱。这表明这 个股票市场的回报率具有一定的 自相关性，即今天的回报率在一 定程度上可以影响到明天的回报 率

95第六章 自相关性课件

95第六章 自相关性课件

2
X
2 t
t，vt随着X
2系统变化，
t
导致了自相关。
5、蛛网现象
表示：某种商品的供给量因受前一期价格影响而表现出来的某
种规律性（如呈蛛网状收敛或发散于供需的品平衡点）如下例（
呈蛛网状收敛）。
10
P
需求曲线
供给曲线
S
P2 Q3
P
0
P3
Q2
Q4
P1
D
Q
Q0
Q1
蛛网现象模型
S P u
t
1
2 t 1
t
即将（3）式：Yt Yt1 1(1 ) 2 ( X t X t1) (ut ut1)
Yt Yt1 2 ( X t X t1 ) (ut ut1 )
Y X
t
2
t
t
由于
t
满足基本假定，即可用OLS对上式进行估计。 23
二、自相关系数未知
1、利用DW统计量求ˆ 因为d 2(1 ˆ )， 所以估算出 ˆ 1 d
15
第三节 自相关性的检验
16
一、图示法
模型的残差et可作为随机干扰项ut估计，如果随机干扰项ut 存在 自相关性的话，必然会由残差序列et反映出来。
绘制et
和et
的相关图
1
（scat
resid
resid(-1)）
15
10
e
5
0
0
5
10
15
17 e(-1)
二、D-W检验
(一) 假定条件 1、假定变量X是非随机的； 2、随机误差项为一阶自回归形式，即
一阶线性自相关： ut ut 1 t
其中： 为随机误差项的自相关系数 ( 1)

第六章 自相关

第六章 自相关

DW检验临界值与三个参数 有关。 （1）检验水平， （2）样本容量T ,
（3）原回归模型中解释变 量个数k（不包括常数项）。
注：1. 表示检验水平，T 表示样本容量， k 表示回归模型中解释变量个数 （不包括常数项） 。 2. dU 和 dL 分别表示 DW 检验上临界值和下临界值。 3. 摘自 Dubrin-Watson (1951)。
Байду номын сангаас
(et et 1 ) 2
DW =
t 2
T
et 2 et 12 2 et et 1
=
t 2 t 2 t 2
T
T
T
et 2
t 1
T
T
et 2
t 1
T T
T
因为在样本容量充分大条件下有 et 2 ≈ e t 1 2 ≈ et 2
t 2 t 2 t 1
2
所以 DW 可以近似表示为， DW≈
e
t 2
T
t 1
2
2
e e
t 2 2
T
t t 1
e e
= 2 (1 t 2 T
T
t t 1
e
t 2
T
t 1
e
t 2
ˆ) ) = 2 (1 -
2
t 1
6.3 自相关检验
与 DW 值的对应关系及意义 =0 =1 = -1
当DW值落在“不确定”区域时，有两种处理方法。（1）加大样本容量或 重新选取样本，重作DW检验。有时DW值会离开不确定区。（2）选用其 它检验方法。 DW检验临界值与三个参数有关。
附表 4
T dL 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 1.08 1.10 1.13 1.16 1.18 1.20 1.22 1.24 1.26 1.27 1.29 1.30 1.32 1.33 1.34 k =1 dU 1.36 1.37 1.38 1.39 1.40 1.41 1.42 1.43 1.44 1.45 1.45 1.46 1.47 1.48 1.48

最新庞浩计量经济学课件第六章-自相关性(组合后)学习资料精品课件

最新庞浩计量经济学课件第六章-自相关性(组合后)学习资料精品课件

)2
故，当原模型随机误差项存在自相关性时，参数OLS估计仍
然存在，且无偏。
19
第十九页，共48页。
自相关(xiāngguān)对OLS估计量方 差的影响
由 ˆ2 2
xtut xt2
Var(ˆ2 ) E(ˆ2 2 )2 E(
xt ut xt 2
)2
(
1 xt 2 )2 E(
xt ut )2
2. u t的自协方差
u t u t 1 v t Co(uvt,ut1)E(utut1)E[(ut1vt)ut1]
u t1 u t2 v t1 u t2 u t3 v t2
E(u2 t1)E(vtut1)1 v22
u t3
u t4
v t3
Cov(ut , ut2 ) E(utut2 ) E[(ut1 vt )ut2]
1.检验步骤
①进对行原O模LS型回归Y t， 求1 出 残2 差X 序2 t 列 ；k X k tu t
②杜宾和沃特森提出假设，并构造出了统计量DW；
n
H0 :（0
即不存在自）相关 DW
t2
(et
n
et1 )2
H1 :（0 即存在自）相关 第二十九页，共48页。
e
2 t
29
t 1
在样本容量足够的情况下（一般要求n大于15）：
其中(qíuzthōng)， 具有一阶线性自回归形式的自相关，
即：
ut ut1vt
v t 满足随机误差项的古典假定，即：
E (vt)0, V(a vt)rv 2,
C(o vt,vts)0(s0),C(o utv 1,vt)0
那么， u t的期望、方差、自协方差分别是什么？
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第六章 案例分析
一、研究目的
2003年中国农村人口占59.47％，而消费总量却只占41.4%，农村居民的收入和消费是一个值得研究的问题。

消费模型是研究居民消费行为的常用工具。

通过中国农村居民消费模型的分析可判断农村居民的边际消费倾向，这是宏观经济分析的重要参数。

同时，农村居民消费模型也能用于农村居民消费水平的预测。

二、模型设定
正如第二章所讲述的，影响居民消费的因素很多，但由于受各种条件的限制，通常只引入居民收入一个变量做解释变量，即消费模型设定为
t t t u X Y ++=21ββ
（6.43）
式中，Y t 为农村居民人均消费支出，X t 为农村人均居民纯收入，u t 为随机误差项。

表6.3是从《中国统计年鉴》收集的中国农村居民1985-2003年的收入与消费数据。

表6.3 1985-2003年农村居民人均收入和消费 单位： 元
2000 2001 2002 2003
2253.40 2366.40 2475.60 2622.24
1670.00 1741.00 1834.00 1943.30
314.0 316.5 315.2 320.2
717.64 747.68 785.41 818.86
531.85 550.08 581.85 606.81
注：资料来源于《中国统计年鉴》1986-2004。

为了消除价格变动因素对农村居民收入和消费支出的影响，不宜直接采用现价人均纯收入和现价人均消费支出的数据，而需要用经消费价格指数进行调整后的1985年可比价格计的人均纯收入和人均消费支出的数据作回归分析。

根据表6.3中调整后的1985年可比价格计的人均纯收入和人均消费支出的数据，使用普通最小二乘法估计消费模型得
t t X Y 0.59987528.106ˆ+=
（6.44）
Se = (12.2238) (0.0214)
t = (8.7332)
(28.3067)
R 2 = 0.9788，F = 786.0548，d f = 17，DW = 0.7706
该回归方程可决系数较高，回归系数均显著。

对样本量为19、一个解释变量的模型、5%显著水平，查DW 统计表可知，d L =1.18，d U = 1.40，模型中DW<d L ，显然消费模型中有自相关。

这一点残差图中也可从看出，点击EViews 方程输出窗口的按钮Resids 可得到残差图，如图6.6所示。

图6.6
残差图
图6.6残差图中，残差的变动有系统模式，连续为正和连续为负，表明残差项存在一阶正自相关，模型中t 统计量和F 统计量的结论不可信，需采取补救措施。

三、自相关问题的处理
为解决自相关问题，选用科克伦—奥克特迭代法。

由模型（6.44）可得残差序列e t ，在EViews 中，每次回归的残差存放在resid 序列中，为了对残差进行回归分析，需生成命名为
e 的残差序列。

在主菜单选择Quick/Generate Series 或点击工作文件窗口工具栏中的Procs/ Generate Series ，在弹出的对话框中输入e = resid ，点击OK 得到残差序列e t 。

使用e t 进行滞后一期的自回归，在EViews 命今栏中输入ls e e (-1)可得回归方程
e t = 0.4960 e t-1
（6.45）
由式（6.45）可知ρ
ˆ=0.4960，对原模型进行广义差分，得到广义差分方程 t t t t t u X X Y Y +-+-=---)4960.0()4960.01(4960.01211ββ
（6.46）
对式（6.46）的广义差分方程进行回归，在EViews 命令栏中输入ls Y -0.4960*Y (-1) c
X -0.4960*X (-1)，回车后可得方程输出结果如表6.4。

表6.4 广义差分方程输出结果 Dependent Variable: Y-0.496014*Y(-1) Method: Least Squares Date: 03/26/05 Time: 12:32 Sample(adjusted): 1986 2003
Included observations: 18 after adjusting endpoints
Variable Coefficient Std. Error t-Statistic Prob. C
60.44431 8.964957 6.742287 0.0000 X-0.496014*X(-1) 0.583287
0.029410
19.83325
0.0000
R-squared
0.960914 Mean dependent var 231.9218 Adjusted R-squared 0.958472 S.D. dependent var 49.34525 S.E. of regression 10.05584 Akaike info criterion 7.558623 Sum squared resid 1617.919 Schwarz criterion 7.657554 Log likelihood -66.02761 F-statistic 393.3577 Durbin-Watson stat
1.397928 Prob(F-statistic)
0.000000
**5833.04443.60ˆt t X Y +=
（6.47）
)9650.8(=Se （0.0294）
t = （6.7423）
（19.8333）
R 2 = 0.9609 F = 393.3577 d f = 16 DW = 1.3979
式中，1*4960.0ˆ--=t t t Y Y Y ，
1*4960.0--=t t t X X X 。

由于使用了广义差分数据，样本容量减少了1个，为18个。

查5%显著水平的DW 统
计表可知d L = 1.16，d U = 1.39，模型中DW = 1.3979> d U ，说明广义差分模型中已无自相关，不必再进行迭代。

同时可见，可决系数R 2
、t 、F 统计量也均达到理想水平。

对比模型（6.44）和（6.47），很明显普通最小二乘法低估了回归系数2ˆ
β的标准误差。

[原模型中Se （2ˆβ）= 0.0214，广义差分模型中为Se （2ˆ
β）= 0.0294。

经广义差分后样本容量会减少1个，为了保证样本数不减少，可以使用普莱斯—温斯
腾变换补充第一个观测值，方法是21*11ρ-=X X 和21*11ρ-=Y Y 。

在本例中即为
210.49601-X 和210.49601-Y 。

由于要补充因差分而损失的第一个观测值，所以在
EViews 中就不能采用前述方法直接在命令栏输入Y 和X 的广义差分函数表达式，而是要生成X 和Y 的差分序列X *和Y *。

在主菜单选择Quick/Generate Series 或点击工作文件窗口工具栏中的Procs/Generate Series ，在弹出的对话框中输入Y *= Y -0.4960*Y (-1)，点击OK 得到广义差分序列Y *，同样的方法得到广义差分序列X *。

此时的X *和Y *都缺少第一个观测值，
需计算后补充进去，计算得*1X =345.236，*
1Y =275.598，双击工作文件窗口的X * 打开序列
显示窗口，点击Edit +/-按钮，将*
1X =345.236补充到1985年对应的栏目中，得到X *的19个观测值的序列。

同样的方法可得到Y *的19个观测值序列。

在命令栏中输入Ls Y * c X*得到普莱斯—温斯腾变换的广义差分模型为
**5833.04443.60t t X Y +=
（6.48）
)1298.9(=Se （0.0297）
t = （6.5178）
（19.8079）
R 2 = 0.9585 F = 392.3519 d f = 19 DW = 1.3459
对比模型（6.47）和（6.48）可发现，两者的参数估计值和各检验统计量的差别很微小，说明在本例中使用普莱斯—温斯腾变换与直接使用科克伦—奥克特两步法的估计结果无显著差异，这是因为本例中的样本还不算太小。

如果实际应用中样本较小，则两者的差异会较大。

通常对于小样本，应采用普莱斯—温斯腾变换补充第一个观测值。

由差分方程（6.46）有
9292
.1194960.014443
.60ˆ1
=-=β
（6.49）
由此，我们得到最终的中国农村居民消费模型为 Y t = 119.9292+0.5833 X t
（6.50）
由（6.50）的中国农村居民消费模型可知，中国农村居民的边际消费倾向为0.5833，即中国农民每增加收入1元，将增加消费支出0.5833元。