ARMA模型案例分析

ARMAARIMA模型介绍及案例分析AR、MA和ARIMA是时间序列分析中常见的模型，用于分析和预测时间序列数据的特征和趋势。

下面将对这三种模型进行介绍，并提供一个案例分析来展示它们的应用。

自回归模型（AR）是一种基于过去的观测值来预测未来观测值的模型。

它基于一个假设：未来的观测值可以由过去的观测值的线性组合来表示。

AR模型的一般形式可以表示为：y_t=c+ϕ_1*y_(t-1)+ϕ_2*y_(t-2)+...+ϕ_p*y_(t-p)+ε_t其中，y_t表示时间t的观测值，c是常数项，ϕ_1至ϕ_p是自回归系数，p是自回归阶数，ε_t是误差项。

AR模型的关键是确定自回归阶数p和自回归系数ϕ。

移动平均模型（MA）是一种基于过去的误差项来预测未来观测值的模型。

它基于一个假设：未来的观测值的误差项可以由过去的误差项的线性组合来表示。

MA模型的一般形式可以表示为：y_t=c+ε_t+θ_1*ε_(t-1)+θ_2*ε_(t-2)+...+θ_q*ε_(t-q)其中，y_t表示时间t的观测值，c是常数项，ε_t是误差项，θ_1至θ_q是移动平均系数，q是移动平均阶数。

MA模型的关键是确定移动平均阶数q和移动平均系数θ。

自回归移动平均模型（ARIMA）结合了AR和MA模型的特点，同时考虑了时间序列数据的趋势性。

ARIMA模型一般形式可以表示为：y_t=c+ϕ_1*y_(t-1)+ϕ_2*y_(t-2)+...+ϕ_p*y_(t-p)+ε_t+θ_1*ε_(t-1)+θ_2*ε_(t-2)+...+θ_q*ε_(t-q)其中，y_t表示时间t的观测值，c是常数项，ϕ_1至ϕ_p是自回归系数，p是自回归阶数，ε_t是误差项，θ_1至θ_q是移动平均系数，q是移动平均阶数。

ARIMA模型的关键是确定自回归阶数p、移动平均阶数q和相关系数ϕ和θ。

下面举一个电力消耗预测的案例来展示AR、MA和ARIMA模型的应用：假设有一段时间内的电力消耗数据，我们想要用AR、MA和ARIMA模型来预测未来一段时间内的电力消耗。

基于ARMA模型的公路货运量预测及分析【摘要】本研究基于ARMA模型对公路货运量进行预测和分析。

首先介绍了ARMA模型的基本原理和应用，然后详细讨论了公路货运量数据的收集和预处理方法。

接着利用ARMA模型对货运量进行预测，并对模型进行了分析和结果讨论。

通过对模型优缺点进行分析，揭示了ARMA模型在货运量预测中的优势和局限性。

最后总结了研究成果并展望了未来的研究方向。

通过本研究，可以为货物运输管理提供决策支持和参考，提高运输效率和减少成本。

ARMA模型在货运量预测中具有一定的应用前景，同时也需要进一步完善和改进，以提高预测准确性和实用性。

【关键词】ARMA模型, 公路货运量, 预测, 分析, 数据收集, 结果讨论, 优缺点分析, 研究总结, 未来研究方向, 研究背景, 研究意义1. 引言1.1 研究背景公路货运是国民经济发展中重要的组成部分，其运输效率直接影响着商品流通和经济发展。

对公路货运量的准确预测可以帮助政府和企业合理调配资源，提高运输效率，降低成本，推动经济的持续发展。

公路货运量受到多种因素的影响，如经济状况、货物需求、交通状况等，预测其变化较为复杂。

传统的预测方法往往依赖于统计分析或经验模型，但这些方法往往对复杂的时间序列数据预测效果不佳。

基于ARMA模型的公路货运量预测成为一种较为有效的方法。

ARMA模型结合了自回归（AR）和移动平均（MA）两种方法，能够较好地捕捉时间序列数据的特征，具有较强的预测能力。

本研究旨在基于ARMA模型对公路货运量进行预测，并对模型进行分析和优缺点评价。

通过对公路货运量数据的收集、预处理和建模，我们希望能够为公路货运行业提供准确的预测结果和决策支持，推动行业的发展和提升运输效率。

1.2 研究意义公路货运量在现代社会经济发展中扮演着重要角色，对国家经济发展和社会稳定起着至关重要的作用。

对公路货运量进行准确的预测和分析具有重要的实践意义和理论价值。

基于ARMA模型的公路货运量预测可以为政府相关部门提供决策支持和参考，帮助其更好地制定交通运输政策和规划，优化道路资源配置，提高运输效率，降低物流成本，推动经济的健康发展。

ARMA模型建模与预测案例分析实验二 ARMA模型建模与预测指导一、实验目的学会通过各种手段检验序列的平稳性;学会根据自相关系数和偏自相关系数来初步判断ARMA模型的阶数p和q，学会利用最小二乘法等方法对ARMA模型进行估计，学会利用信息准则对估计的ARMA模型进行诊断，以及掌握利用ARMA模型进行预测。

掌握在实证研究中如何运用Eviews软件进行ARMA模型的识别、诊断、估计和预测和相关具体操作。

二、基本概念宽平稳:序列的统计性质不随时间发生改变，只与时间间隔有关。

AR模型:AR模型也称为自回归模型。

它的预测方式是通过过去的观测值和现在的干扰值的线性组合预测，自回归模型的数学公式为:yyyy,，，，，,,,, tttptpt1122,,,,,y式中: 为自回归模型的阶数(i=1，2，，p)为模型的待定系数，为误差，为？pitt一个平稳时间序列。

MA模型:MA模型也称为滑动平均模型。

它的预测方式是通过过去的干扰值和现在的干扰值的线性组合预测。

滑动平均模型的数学公式为:y,,,,,,,,,,,, ttttqtq1122,,,,,y式中: 为模型的阶数; (j=1，2，，q)为模型的待定系数;为误差; 为平稳？qjtt时间序列。

ARMA模型:自回归模型和滑动平均模型的组合，便构成了用于描述平稳随机过程的自回归滑动平均模型ARMA，数学公式为:yyyy,，，，，,,,,,,,,,,,,,, tttptptttqtq11221122,,,,,,三、实验内容及要求1、实验内容:(1)根据时序图判断序列的平稳性;(2)观察相关图，初步确定移动平均阶数q和自回归阶数p;(3)运用经典B-J方法对某企业201个连续生产数据建立合适的ARMA()模型，并pq,能够利用此模型进行短期预测。

2、实验要求:(1)深刻理解平稳性的要求以及ARMA模型的建模思想;(2)如何通过观察自相关，偏自相关系数及其图形，利用最小二乘法，以及信息准则建立合适的ARMA模型;如何利用ARMA模型进行预测;(3)熟练掌握相关Eviews操作，读懂模型参数估计结果。

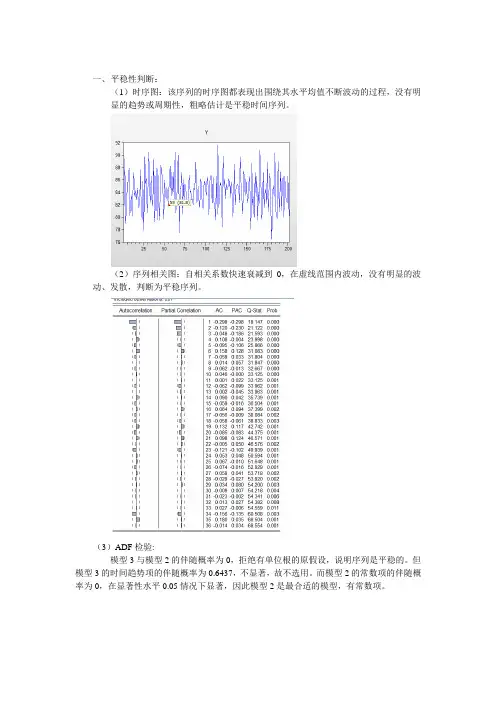
一、平稳性判断：（1）时序图：该序列的时序图都表现出围绕其水平均值不断波动的过程，没有明显的趋势或周期性，粗略估计是平稳时间序列。

（2）序列相关图：自相关系数快速衰减到0，在虚线范围内波动，没有明显的波动、发散，判断为平稳序列。

（3）ADF检验:模型3与模型2的伴随概率为0，拒绝有单位根的原假设，说明序列是平稳的。

但模型3的时间趋势项的伴随概率为0.6437，不显著，故不选用。

而模型2的常数项的伴随概率为0，在显著性水平0.05情况下显著，因此模型2是最合适的模型，有常数项。

模型1的t检验的伴随概率为0.6128，不能拒绝有单位根的原假设，不选用。

综上所述，该序列是平稳的。

二、随机性检验观察自相关图最后两列可以看到，Q检验的伴随概率均小于0.05，拒绝没有自相关性的原假设，因此该序列不是白噪声序列，没有把信息都提取出来。

观察其AC，虽落入虚线内后没有再到虚线外，但不是由非0骤降到0，判断为拖尾。

观察PAC，结果与AC类似，因此AC、PAC都是拖尾，初步判断使用ARMA模型。

接下来将尝试使用AR（１）、AR（２）、MA（１）、MA（２）、ARMA（1，3）、ARMA（1，2）模型进行拟合。

三、模型估计与白噪声检验（１）AR（１）：该模型各项显著，故对其进行残差项白噪声检验，观察Q检验及其伴随概率，在显著性水平为0.05时，拒绝没有自相关性的原假设，不是白噪声序列。

（２）AR（2）：该模型各项显著，故对其进行残差项白噪声检验，观察Q检验及其伴随概率，在显著性水平为0.05时，阶数较小时拒绝没有自相关性的原假设，不是白噪声序列。

（３）MA（１）：该模型各项显著，故对其进行残差项白噪声检验，观察Q检验及其伴随概率，在显著性水平为0.05时，接受没有自相关性的原假设，是白噪声序列。

（４）MA（2）：该模型MA（２）项不显著，不选用。

（５）ARMA（1，3）：该模型各项显著，故对其进行残差项白噪声检验，观察Q检验及其伴随概率，在显著性水平为0.05时，接受没有自相关性的原假设，是白噪声序列。

ARMAARIMA模型介绍及案例分析ARMAARIMA模型是一种时间序列分析方法，用于对具有自回归和移动平均特性的数据进行建模和预测。

这个模型是由自回归（AR）和移动平均（MA）两个组成部分构成的，对于非平稳的数据还需要加入差分（I）的过程，所以称为ARMAARIMA模型。

ARMA模型是根据时间序列的自相关和滑动平均性质来进行建模的。

自回归是指当前数据与历史数据之间的相关关系，移动平均则关注当前数据与滞后差分误差之间的关系。

ARMA模型的一般形式可以表示为：Y(t)=c+φ₁Y(t-1)+...+φₚY(t-p)+ε(t)-θ₁ε(t-1)-...-θₚε(t-q)其中，Y(t)表示当前的观测值，c是常数，φ₁...φₚ是自回归系数，ε(t)是白噪声误差项，θ₁...θₚ是滑动平均系数，p和q分别表示AR和MA的阶数。

对于非平稳的时间序列数据，需要进行差分操作，即I（积分）的过程，来将数据变为平稳的。

差分阶数常用d表示。

而ARIMA（自回归移动平均积分模型）则是对ARMA模型进行补充，主要针对非平稳时间序列数据。

ARIMA模型的一般形式可以表示为：ΔY(t)=c+φ₁ΔY(t-1)+...+φₚΔY(t-p)+ε(t)-θ₁ε(t-1)-...-θₚε(t-q)其中ΔY(t)表示差分后的序列，其他参数与ARMA模型类似。

下面以一个股票价格的时间序列数据为例进行ARMAARIMA模型的案例分析。

假设我们有一段时间内的股票价格数据，要通过ARMAARIMA模型对未来的股票价格进行预测。

首先，我们需要对数据进行平稳性检验，可以使用单位根检验（如ADF检验）来确定是否需要进行差分。

接下来，需要确定ARMA模型的阶数，可以通过观察自相关图（ACF）和偏自相关图（PACF）来确定。

根据图形的截尾和拖尾情况，可以估计出AR和MA的阶数。

然后，可以利用最大似然估计方法来估计模型参数，这可以通过软件来实现。

在估计参数之后，需要对模型进行检验，主要包括检查残差序列是否为白噪声，可以通过自相关图和偏自相关图进行检查。

Arma模型步骤及案例分析ar:自回归auto-regression Arma modelma:移动平均moving average （Ɛ随机干扰random disturbing）步骤一．平稳性检验（单位根检验unit root test）原理：y=ay+Ɛ当回归系数a等于1时，y为单位根过程即y=-y+Ɛ单位根过程=不平稳过程（non-station）=随机漫步（醉步，random walk）注：与平稳过程对应的是平稳过程（猫步，station）案例采取1978年到2005年的居民消费数据在EViews中建立文件，录入数据，取名为XF注；通过file成功建立一个workfile后，点击proc,下拉菜单里面有个import,点击后选择read text-lotus-excel,然后就可以选择你要导入的excel文件了。

不过注意：该文件一定要用英文命名，而且存储路径最好也是英文的。

检验过程：1View→graph→line(视图→图表→曲线图)2view→unit root test→3（注：level为水平序列1st different为一阶差分2nd different为二阶差分；intercept为截距基数trend and intercet为趋势和基数，比较常用；Lag length为后置长度，一般选用自动选择）4出结果根据P值若prob*>a则换用1st差分，以此类推。

本案例中是取二阶差分(注：null hypothesis（原假设）H0：“arimo1”has a unit root H1:“arimo1”has not a unit root)步骤二.建模Quick→Estimate Equation（注：填写d（xf,2）ar(p)ma(q)p属于[0,3]）q[0,3]，此步骤中确定p，q取值是要点）1注：Schwarz criterion施瓦茨准则（最关键，越小越好）Akaike info criterion赤池信息准则（平均预测误差，越小越好）2在p，q的几个取值结果中，寻找SC最小的作为最优选择3View→representations结果为抽样模型步骤三.白噪声检验（W.N.Test纯粹随机性检验）View→Residual Tests→serial correlation LM test(序列相关的拉格朗日乘数检验)→lags to2OK1)注：H0：序列（残差序列，剩余数列，扰动序列）无关H1：序列相关2)“希望接受H0”本案例中，pro>a=0.05,接受H03)对于时间序列用W.N test对于截面数据用D.W test步骤四.预测（forecast）单击Forecast结果如下单击OK，结果是打开xff(本案例的预测变量)为。

ARMA模型案例假设我们有一组历史销售数据，我们希望使用ARMA模型来预测未来销售量。

首先，我们需要进行数据的预处理，包括数据清洗和转化。

这包括去除异常值、填充缺失值以及将数据转化为平稳序列。

接下来，我们可以通过观察时序图和自相关图来确定ARMA模型的阶数。

时序图是展示时间序列的变化趋势和规律的图表，自相关图则展示了时间序列与其滞后版本之间的关联性。

通过分析这些图表，我们可以确定ARMA模型的阶数，即p和q值。

假设我们发现销售数据呈现出一定的周期性和趋势性，且自相关图呈现出指数递减的模式。

这提示我们可以使用ARMA(p,q)模型来建模。

在此案例中，我们选择p=3，q=2然后，我们需要估计ARMA模型的参数。

可以使用似然函数或最小二乘法进行参数估计。

估计出参数后，我们可以使用模型对未来销售量进行预测。

接下来，我们可以使用拟合优度检验来评估模型的拟合程度。

常用的拟合优度检验方法包括均方根误差（RMSE）和残差自相关函数。

如果拟合优度检验结果不理想，我们可以尝试使用不同的ARMA模型阶数来改进模型的拟合。

最后，我们可以使用建立的ARMA模型进行未来销售量的预测。

通过输入新的自变量数据，我们可以得到相应的因变量（销售量）的预测值。

需要注意的是，ARMA模型仅适用于平稳时间序列。

如果数据包含明显的趋势或季节性，我们需要先对数据进行差分或季节性调整，然后再应用ARMA模型。

综上所述，ARMA模型是一个常用的时间序列建模方法，在许多领域都有广泛的应用。

通过选择适当的ARMA模型阶数、估计参数以及拟合优度检验，我们可以使用ARMA模型对未来的销售量进行准确的预测。

同时，我们也可以根据预测结果进行相应的决策，以优化业务运营和管理。

基于ARMA模型的股价短期预测——以古井贡酒股票为例基于ARMA模型的股价短期预测——以古井贡酒股票为例概述：股票市场一直以来都备受关注。

投资者们希望通过分析历史股票数据，预测股价的未来走势，从而做出更理性的投资决策。

传统的统计模型中，ARMA模型作为时间序列分析中的一种经典方法，被广泛用于股票价格的预测。

本文以古井贡酒股票为例，探讨了基于ARMA模型的股价短期预测方法及其应用。

第一部分：古井贡酒及其股票背景介绍古井贡酒是中国知名的白酒品牌之一，成立于1955年，总部位于河南省。

作为中国国内外都有广泛知名度的酒企，其股票一直备受市场关注。

随着中国白酒市场的逐渐增长和消费升级的趋势，投资古井贡酒股票成为一项备受关注的投资活动。

第二部分：ARMA模型基本原理和公式推导ARMA模型是一种时间序列分析模型，由自回归（AR）模型和滑动平均（MA）模型组成。

AR模型是根据自身过去的观测值来预测未来的观测值，而MA模型是根据过去的误差值来预测未来的观测值。

因此，ARMA模型综合了过去观测值和误差值的信息，用于预测未来的时间序列。

第三部分：古井贡酒股价数据的收集和预处理为了建立ARMA模型，我们需要收集一段时间内的古井贡酒股价数据。

首先，我们可以从公开的金融数据网站获得每日的股价数据。

然后，对数据进行预处理，包括去除异常值、填充缺失值、平滑数据等，以确保数据的准确性和合理性。

第四部分：ARMA模型的参数估计及模型诊断在建立ARMA模型之前，我们需要确定模型的阶数。

阶数的确定可以通过自相关函数（ACF）和偏自相关函数（PACF）的分析来实现。

通过观察ACF和PACF的图形，获得AR和MA 的阶数，并用这些阶数拟合ARMA模型。

然后，我们使用最小二乘法（OLS）对ARMA模型的参数进行估计。

通过极大似然方法，我们可以找到最有可能产生实际观测值的ARMA模型参数。

最后，我们使用残差分析、自相关图和偏自相关图来诊断ARMA模型的拟合效果。

基于ARMA模型的我国商品房屋价格的分析我国自1998年实行货币化分房政策以来，房地产业的快速发展极大地改善了我国居民的居住条件。

但是，与此相伴的日益高涨的房价却让中国广大居民望房兴叹，无力买房。

同时也促使政府对房价调控措施频出，2007年底，国家出台了《经济适用住房管理办法》来增加经济适用房的供给，抑制炒房行为。

在这种房价一路看涨和政府宏观调控措施频出的特殊博弈中，未来中国商品房屋的走势会如何是国内学者普遍关注的问题，本文运用ARMA模型，通过对房屋销售价格的历史数据的内部挖潜和分析，希望能找到一个未来我国商品房屋价格走势的方向，为政府进一步宏观调控提供一定得依据。

一、数据收集及处理本文的数据采用全国范围时间序列数据，时间跨度为1991年到2008年。

具体数据如下：表一我国历年房屋销售价格只有平稳的时间序列才能够直接建立ARMA模型，所以要对序列的平稳性做检验。

检验是否平稳的客观方法主要是单位根检验。

单位根检验的方法有很多种，本文主要利用了ADF检验，其检验的方程模型如下：这三个模型分别是没有常数项和时间趋势的；仅有常数项，没有时间趋势的；以及含有常数项和时间趋势的。

其原假设与备择假设分别为：；。

根据对商品房屋价格（）的初步分析，认为选用第二个模型进行检验较为合适，并且选择滞后阶数P为3阶。

利用Eviews计算，得出不拒绝原假设的概率为0.9978，说明没有充分的理由拒绝原假设，显然参数显著的为0，则商品房屋价格序列存在单位根，故该序列不是平稳的。

由于不平稳的数据不能建立ARMA模型，所以建模之前首先要对数据进行预处理，将其变为平稳的时间序列。

本文从商品房屋价格的增长率的变化进行分析，首先利用同样的方法对房屋价格增长率序列进行平稳性检验，得到在95%的置信水平下该序列为不平稳序列。

在对商品房屋价格增长率的一次差分进行平稳性检验， ADF检验表明在95%的置信水平下拒绝原假设，认为该序列不存在单位根。

针对乳制品月产量数据的时间序列分析摘要：随着经济的发展，乳制品产业对国民健康水平的影响逐渐加大。

该文从乳制品行业月产量的角度出发，采用时间序列数据分析方法，对我国自1990年至2010年以来的乳制品行业月产量进行了建模分析，并在得到模型后对其进行了预测。

从分析结果来看，我国的乳制品产量在2004年发生突变，特定的月份也会对其产生影响，并且在不同的时间，影响会发生变化。

关键词：乳制品；月份特征；产量突变；产量预测；背景：纵观自1949年发展至今，整个行业可以分为四个发展阶段：1、缓慢发展阶段（1949~1977）：这段时期，我国乳产业受国家经济状况制约发展缓慢。

2、迅速扩张阶段（1978~1992）：由于开始实行多种所有制进行奶牛饲养与奶制品加工，原奶与乳品的产量、种类、质量都有明显的提高3、结构调整阶段（1993~1998）：1993年开始，乳品供给增长明显快于消费增长速度，产能出现比较严重的过剩，乳粉出现滞积，部分乳品企业发展艰难。

4、高速增长阶段（1999~至今）：1998年起，乳制品产业经过产品结构大力调整，经济效益明显提高，随着消费需求的迅速增长，乳制品产量也连年增长，乳产业已经从一个传统产业摇身一变成为一个朝阳产业。

从市场格局上看，乳制品企业可以分为4类：1、以伊利、蒙牛为代表的全国性企业；2、以光明、三鹿、维维等为代表的区域性企业；3、以北京三元、济南佳宝为代表的本省省会企业；4、以雀巢为代表的外资企业。

在行业中，企业之间的竞争非常激烈，特别地，在近十年中市场竞争引起了市场格局的极大改变。

本文将选取1993年1月起到2010年6月的月产量数据进行时间序列分析，尝试建立该时序的时间序列模型及其详细的建立过程，并对模型结果给出必要的经济意义解释。

建立模型过程：1、建模过程使用eviews软件，将1990年1月到2010年6月总计246个月度数据输入eviews中，Yt即是产量月度序列，现作出散点图如下：通过观察上图，认为不同时间下的Yt的数值差异过大，并且波动程度也差别过大，故先将序列作取对数处理，作出散点图如下：通过观察上图，认为该序列是一个典型的结构突变的过程，突变位置始于2003年12月。

AND ———以中信银行为例谢海宁，尚园（武汉纺织大学，武汉430200）摘要：通过EVIEWS 软件，根据中信银行（股票代码：601998）2018年1月1日至2019年12月31日的股票日开盘价建立ARMA 模型，由于影响股票价格的因素很多，股票价格的走势往往是不稳定的，故采取差分法对股票价格序列进行差分，使其平稳化，以差分后的序列为基础进行建模分析，然后预测中信银行未来22日的股票价格，将预测得出的股票价格与实际观测值进行比较分析，绘制趋势图可以看出，前15日的估测值与实际值误差偏离程度较小，后5日的估测值与实际值误差偏离程度较大。

因此，得出结论，ARMA 模型能够对短期内的股票价格进行很好的预测，但是长期来看，股票价格受到多重因素影响，ARMA 模型进行长期预测时会存在较大的误差。

最后，针对预测结果为投资者提供合理的投资建议。

关键词：中信银行；ARMA 模型；EVIEWS ；股票价格中图分类号：F290文献标识码：Ａ文章编号：1005-913X （2020）12-0122-03收稿日期：2020-07-07作者简介：谢海宁(1994-)，女，安徽安庆人，硕士研究生，研究方向：公司金融与税收筹划；尚园(1994-)，女，山东菏泽人，硕士研究生，研究方向：风险投资与资本市场。

1984年，我国第一支股票公开发行预示着我国金融市场迎来了改革开放，进入21世纪以后，股票投资已经成为国民理财不可缺少的一部分。

对于投资者来说，能够预测股票未来发展趋势对于其投资理财规划具有非常深刻的意义。

伴随着股票市场的繁荣，股民们不断寻求各种办法判断选择最优的投资组合，追求最大化自身收益。

近年来，国内外都由此兴起了数家围绕着股票价格进行预测的社交平台，网友们自由发表自己预测股票价格走势的经验，学者们也在积极研究更加精准有效的股票价格预测算法。

本文将主要对ARMA 模型进行介绍，以中信银行历史数据建模，建立股票价格预测模型预测其未来一个月中信银行（股票代码：601988）的股票价格走势。