双模圆锥喇叭天线的设计课件

微波技术与天线课程设计——角锥喇叭天线姓名：***学号：**********目录一．角锥喇叭天线基础知识 (3)1. 口径场 (3)2. 辐射场 (4)3.最佳角锥喇叭 (7)4. 最佳角锥喇叭远场E 面和H面的主瓣宽度 (7)二．角锥喇叭设计实例 (7)1. 工作频率 (8)2.选用作为激励喇叭的波导 (8)3.确定喇叭的最佳尺寸 (8)4.喇叭与波导的尺寸配合 (9)5.天线的增益 (10)6.方向图 (10)一．角锥喇叭天线基础知识角锥喇叭是对馈电的矩形波导在宽边和窄边均按一定张角张开而形成的，如下图所示。

矩形波导尺寸为a×b，喇叭口径尺寸为D H×D E，其E面(yz 面)虚顶点到口径中点的距离为R ，H 面(xz 面)内虚顶点到口径中点的距离为R E,H 面(xz 面)内虚顶点到口径中点的距离为R H。

1. 口径场角锥喇叭内的电磁场，目前还未有严格的解析解结果，原因在于，角锥喇叭在x和y两个方向随喇叭的长度方向均是渐变而逐渐扩展的，因而要在一个正交坐标系下求得角锥喇叭内的场的严格解析解是困难的。

通常近似地认为，矩形角锥喇叭中的电磁场具有球面波特性，而且假设角锥喇叭口径面上的相位分布沿x和y两个方向均为平方律变化。

按此假设，可写出角锥喇叭的口径场为：ηπβyX R y R x j H y E H eD xE E EH -==+-)2(022)cos( （1.1）如果是尖顶角锥喇叭，则 R H ＝ R E ，可用作标准增益喇叭。

若是楔形喇叭，则R H ≠R E 。

由此口径面场分布计算的远场与实测的结果吻合的很好，说明了假设的口径场分析模型的正确性。

2. 辐射场由角锥喇叭的口径场分布，仿照前面求 E 面和 H 面扇形喇叭远区辐射场的步骤，就可以求出角锥喇叭的远区辐射场表达式。

由于计算过程较繁，这里直接给出结果。

])cos 1([cos 2])cos 1([sin 200H E r j H E r j I I re E j E I I r e E j E θϕλθϕλβϕβθ+=+=-- （2.1）其中：)]})()([)()({)]}()([)()({(213434)2/(1212)2/(2221u S u S j u C u C eu S u S j u C u C e R I H x H x R j R j H H +-+++-+=--βββββπ（2.3）)]}()([)()({211212)2/(2w S w S j w C w C e R I E Y R j E E +-+=-βββπ（2.4）H x Hx D D /cos sin /cos sin 21πϕθββπϕθββ-=+= (2.5)HH x H H H x H HH x H H H x H R R D u R R D u R R D u R R D u πβββπβββπβββπβββ/)2/(/)2/(/)2/(/)2/(21211111-=+=-=+= (2.6))sin sin 2()sin sin 2(21ϕθπβϕθπβE EE E EE R D R w R D R w -=+= （2.7） 角锥喇叭的 E 面和 H 面场为：2/||====ϕϕπϕθE E E E H E (2.8)在角锥喇叭的 D E 、R E 、D H 、R H 与扇形喇叭的相同时，可以证明:■角锥喇叭在 E 面的方向图与 E 面扇形喇叭的 E 面方向图相同；■角锥喇叭在 H 面内的方向图与 H 面扇形喇叭在 H 面内的方向图相同。

微波技能与天线课程安排——之阳早格格创做角锥喇叭天线姓名：吴爽教号：1206030201目录一．角锥喇叭天线前提知识34. 最好角锥喇叭近场 E里战 H里的主瓣宽度7二．角锥喇叭安排真例7一．角锥喇叭天线前提知识角锥喇叭是对付馈电的矩形波导正在宽边战窄边均按一定弛角弛启而产生的，如下图所示.矩形波导尺寸为a×b，喇叭心径尺寸为D H×D E，其E里(yz 里)真顶面到心径中面的距离为R ，H 里(xz 里)内真顶面到心径中面的距离为R E,H 里(xz 里)内真顶面到心径中面的距离为R H.1. 心径场角锥喇叭内的电磁场，暂时还已有庄重的剖析解截止，本果正在于，角锥喇叭正在 x战 y二个目标随喇叭的少度目标均是渐变而渐渐扩展的，果而要正在一个正接坐标系下供得角锥喇叭内的场的庄重剖析解是艰易的.常常近似天认为，矩形角锥喇叭中的电磁场具备球里波个性，而且假设角锥喇叭心径里上的相位分散沿x 战 y 二个目标均为仄圆律变更.按此假设，可写出角锥喇叭的心径场为：ηπβy X R y R x j H y E H e D x E E EH -==+-)2(022)cos(（1.1）如果是尖顶角锥喇叭，则 R H ＝ R E ，可用做尺度删益喇叭.假如楔形喇叭，则R H ≠R E .由此心径里场分散估计的近场与真测的截止符合的很好，道明白假设的心径场分解模型的精确性.2. 辐射场由角锥喇叭的心径场分散，仿照前里供 E 里战 H 里扇形喇叭近区辐射场的步调，便不妨供出角锥喇叭的近区辐射场表白式.由于估计历程较繁，那里间接给出截止.])cos 1([cos 2])cos 1([sin 200H E rj H E rj I I r e E j E I I re E j E θϕλθϕλβϕβθ+=+=-- （2.1） 其中：)]})()([)()({)]}()([)()({(213434)2/(1212)2/(2221u S u S j u C u C e u S u S j u C u C e R I H x H x R j R j H H+-+++-+=--βββββπ （2.3）)]}()([)()({211212)2/(2w S w S j w C w C e R I E Y R j E E +-+=-βββπ（2.4） H x Hx D D /cos sin /cos sin 21πϕθββπϕθββ-=+= (2.5)H H x H HH x H HH x H HH x H R R D u R R D u R R D u R R D u πβββπβββπβββπβββ/)2/(/)2/(/)2/(/)2/(21211111-=+=-=+= (2.6))sin sin 2()sin sin 2(21ϕθπβϕθπβE E E E E E R D R w R D R w -=+= （2.7）角锥喇叭的 E 里战 H 里场为： 02/||====ϕϕπϕθE E E E H E (2.8)正在角锥喇叭的 D E 、R E 、D H 、R H与扇形喇叭的相共时，不妨道明:■角锥喇叭正在 E 里的目标图与 E 里扇形喇叭的 E 里目标图相共；■角锥喇叭正在 H 里内的目标图与 H 里扇形喇叭正在 H 里内的目标图相共.决定(与γ/β =1 ).画出的幅度三维图及 E 里战 H 里目标图如下图所示：是指角锥喇叭的尺寸正在 H 里战 E 里分别与最好，即 λλ2322E Eop H HopD R D R ==43ϕπϕ= (3.1)那样，便可使角锥喇叭的删益为最大.4. 最好角锥喇叭近场 E 里战 H 里的主瓣宽度Z 由于正在相共的 R E 战 D E 条件下， 角锥喇叭的E 里目标图与 E 里扇形喇叭的E 里目标图相共，正在相共的 RH 战 DH 条件下，角锥喇叭的 H 里目标图与 H 里扇形喇叭的目标图相共，则最好角锥喇叭 E 里战 H 里目标图的主瓣宽度分别由式(4.1)战(4.2)表示，即：2θλ/D 1 rad=80λ/D 1(°) (4.1)2θλ/D 1 rad=54λ/D 1(°) (4.2)角锥喇叭做天线时，可按此央供安排.二．角锥喇叭安排真例1.处事频次教号：12060302011000+50+1500=2500MHZ波少λ波导的尺寸a,b应包管波导内只传输TE10波.果此采用λ=λ笔曲极化，电场目标笔曲于大天已给定波束宽度火仄里：2θλ/D1 rad=80λ/D1(°)供得 D1=0.9408m （2θ=10）笔曲里：2θλ/D1 rad=54λ/D1(°)供得 D2=0.42336m （2θ=15）决定尺寸D1，D2喇叭尺寸决定后，由喇叭最好尺寸公式：R H=D12/3λR E=D22/2λ供出喇叭的少度：R HR E对付于角锥喇叭天线，末尾决定其尺寸时，还要思量喇叭有波导正在颈部的尺寸协共问题，如下图所示：代进得到闭系式：考证：而将R E 建改为cm R H 51.2995116.0=9.182451.0212==D D G λπ=45.5 Db表里估计公式：角锥喇叭E 里目标图战H 里目标图分别为对付应的E 里扇形喇叭的E 里目标图战H 里扇形喇叭的H 里目标图.E 里目标图：其中：⎪⎭⎫ ⎝⎛--=θπsin 2222'1R D R k tH 里目标图：其中：⎪⎭⎫ ⎝⎛--=1'11'121R k kD kR t x π dt t x C x ⎰=02)2cos()(π <余弦Fresnel 积分>dt t x S x ⎰=02)2sin()(π<正弦Fresnel 积分> Matlab 源步调：E 里目标图clcclear%a=input('请输进角锥输进端宽度（H 里）单位mm a=') a=8.5;a=a*10.^(-3);%b=input('请输进角锥输进端宽度（E 里）单位mm b=') b=4;b=b*10.^(-3);%D1=input('请输进角锥心径宽度（H 里）单位mm A=') D1=94;D1=D1*10.^(-3);%D2=input('请输进角锥心径宽度（E 里）单位mm B=')D2=42.3;D2=D2*10.^(-3);%h=input('请输进喇叭心少度单位mm H=')h=227;h=h*10.^(-3);%f=input('请输进处事频次单位0.1MHZ f=')f=25500;f=f*10.^6;lamd=3*10.^8/f;R2=h/(1-b/D2);theta=-60:0.2:60;k=2*pi/lamd;theta1=theta.*pi/180;t1_1=sqrt(k/(pi*R2)).*(-(D2/2)-R2.*sin(theta1));t2_1=sqrt(k/(pi*R2)).*((D2/2)-R2.*sin(theta1)); EE=exp(j.*(k.*R2.*(sin(theta1))./2)).*F(t1_1,t2_1); FE=-j.*(a*sqrt(pi*k*R2)/8).*(-(1+cos(theta1))*(2/pi)*(2/pi).*EE);FE1=abs(FE);FE1=FE1./max(FE1);FEdB=20*log10(FE1);figure(1)plot(theta,FEdB);grid ontitle('角锥喇叭E里目标图')xlabel('Angle(\theta)/\ circ')ylabel('Gain(\theta)')H里目标图R1=h/(1-a/D1);theta=-60:0.2:60;k=2*pi/lamd;theta1=theta.*pi/180;kx_1=k.*sin(theta1)+pi/D1;kx_11=k.*sin(theta1)-pi/D1;f1=kx_1.*kx_1*R1/(2*k);f2=kx_11.*kx_11*R1/(2*k);t1_1=sqrt(1/(pi*k*R1)).*(-(k*D1/2)-kx_1*R1);t2_1=sqrt(1/(pi*k*R1)).*((k*D1/2)-kx_1*R1);t1_11=sqrt(1/(pi*k*R1)).*(-(k*D1/2)-kx_11*R1);t2_11=sqrt(1/(pi*k*R1)).*((k*D1/2)-kx_11*R1);FF=exp(j.*f1).*F(t1_1,t2_1)+exp(j.*f2).*F(t1_11,t2_11); FH=j.*(b/8).*sqrt((k*R1/pi)).*((1+cos(theta1)).*FF); FH1=abs(FH);FH1=FH1./max(FH1);FHdB=20*log10(FH1);figure(1)plot(theta,FHdB);grid ontitle('角锥喇叭H里目标图')xlabel('Angle(\theta)/\ circ')ylabel('Gain(\theta)')所用子函数F：%%F(t1,t2)=[C(t2)-C(t1)]-j[S(t2)-S(t1)] function y=F(t1,t2)C2=mfun('FresnelC',t2);C1=mfun('FresnelC',t1);S2=mfun('FresnelS',t2);S1=mfun('FresnelS',t1);y=(C2-C1)-j.*(S2-S1);end。

0.8~2.5 GHz 双极化四脊圆锥喇叭天线设计
0 引言
喇叭天线由于其多功能性、简单性和好的辐射性能，在微波测量、雷达和探测系统中有广泛的应用。

展宽喇叭天线工作频带，最直接的方法就是在喇叭的波导和喇叭张开部分加入脊结构。

脊喇叭天线增益高，阻抗低，体积小，易于和传输线连接，适合用在雷达、电子对抗设备以及微波电子器件中。

喇叭天线作为馈源组阵时，圆锥喇叭可以节省空间，便于控制阵元间距而抑制栅瓣。

近来对加脊喇叭天线分析的文章很多，但是在具体的设计方面分析的很少。

本文对设计四脊圆锥喇叭天线的关键参数进行了分析以及仿真优化。

加脊的喇叭天线极大地满足了在宽频带天线领域的应用。

1 天线设计及优化
1.1 天线的设计
脊喇叭天线是在喇叭天线的基础上，通过改变天线的结构来提升辐射性能。

该喇叭天线作为馈源组阵，所以在天线设计过程中应综合考虑喇叭的口径与阵元间距的关系，既要避免溢出损耗，又要保证单元尺寸不要超过最大阵元间距而无法排布。

四脊喇叭可以看成两个对称的双脊喇叭，通过对脊波导理论的分析，根据设计参数指标的要求，设计出满足要求的四脊波导的结构和喇叭内脊曲线的形式，最终完成天线结构的设计。

脊喇叭结构如图1 所示。

喇叭馈电采用同轴线馈电，同轴线的内外径设计保证和50 &Omega;匹配。

根据同轴线特性阻抗公式：
$1.。

式中：a 为同轴线内导体的直径;b 为外导体的直径;&epsilon;r 为导体间填充。

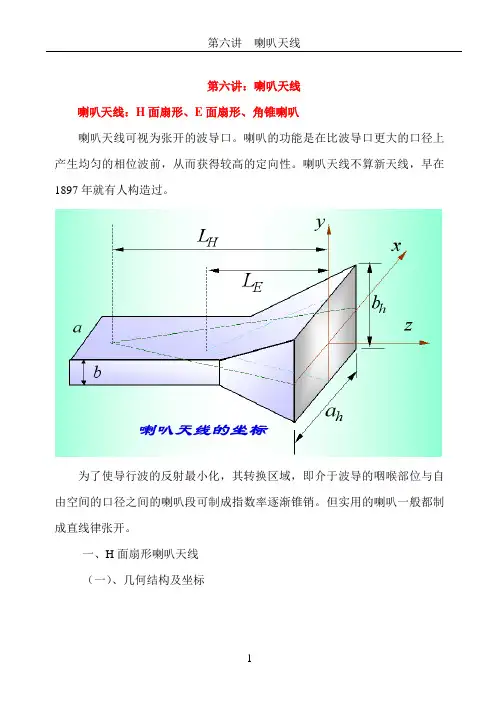
第六讲：喇叭天线喇叭天线：H面扇形、E面扇形、角锥喇叭喇叭天线可视为张开的波导口。

喇叭的功能是在比波导口更大的口径上产生均匀的相位波前，从而获得较高的定向性。

喇叭天线不算新天线，早在1897年就有人构造过。

为了使导行波的反射最小化，其转换区域，即介于波导的咽喉部位与自由空间的口径之间的喇叭段可制成指数率逐渐锥销。

但实用的喇叭一般都制成直线律张开。

一、H面扇形喇叭天线（一）、几何结构及坐标1D2D b=O一段尺寸为a b⨯的矩形波导口径沿H面渐变，张开形成口经为1D b⨯的喇叭—H面扇形喇叭。

矩形波导的宽边为a，窄边为b，传输10TE 模，假定波导开口面上的场分布和波导内横截面上的场分布相同。

两个渐变壁的交线为Y轴，口径法向为Z轴，Y与Z轴交O点，口径中心为O’点，1OO R H'=-称为面扇形喇叭的长度HHα-面扇形喇叭的半张角(二)、内场1、内场表达式假设喇叭无限长，采用圆柱坐标系(ρα，，y )，喇叭内为空气介质。

设波导传输横电模（TE 模），则内场为：$µµ(,,)(,,)(,,)(,,)(,,)y E y yE y H y H y H y αρραραρααραρρα⎧=⎪⎨=+⎪⎩u v u u v 由于H 面沿Y 向无变化，故场与Y 坐标无关，或说Y 向均匀分布。

(,,)(,)(,,)(,)y y E y E H y H ααρρραραραρα=⎧⎪⎨=⎪⎩ 在圆柱坐标系中，由Maxwell 方程可得关于内场的微分方程222222211()()0zk ρϕρρρρρϕ∂A ∂A ∂A ∂∇A =++∂∂∂∂∇+A =2柱坐标系中z 波动方程 222211()1y y y o yo E E k E Eyj H E j H ραρρρρραωμραωμρ∂∂∂=--∂∂∂∂-=∂∂-=∂ 其中，2200,k k ωεμ=为波数 可见，只需求解出y E 即可，,H H ρα由y E 求得。

桂林电子科技大学实验报告 2015 -2016 学年第一学期
开课单位海洋信息工程学院
适用年级 13级电子信息工程
课程名称无线传感器网络
主讲教师
课程序号 1510380
课程代码 BT1605010X0
实验名称圆形口径双模喇叭天线设计
实验学时 6
学号 13160304
姓名
圆形口径双模喇叭天线设计
一、实验目的
利用电磁软件Ansoft HFSS设计一款圆形口径双模喇叭天线。

在仿真实验的帮助下对各种微波元件有个具体形象的了解。

二、实验原理
圆形口径喇叭天线通常称为圆锥喇叭天线，双模圆锥喇叭通过TE11模和TM11模的适当综合
获取轴对称的等化波束方向图和低的交叉极化电平.由于双模圆锥喇叭具有结构简单的突出优点,对于窄频带的反射面天线系统。

原理图：
仿真图：
实验总结
经过这次实验，让我明白了分析的重要性，还有专业知识的掌握性，我们应该大量学习。