当前位置：文档之家 › 方波信号的傅里叶变换

方波信号的傅里叶变换

  • 格式：ppt
  • 大小：1.50 MB
  • 文档页数：82

下载文档原格式

  / 82

合集下载

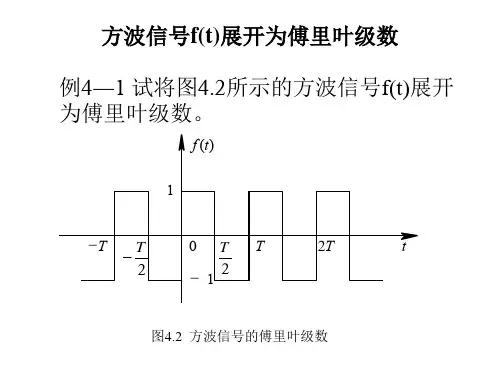
方波信号的傅里叶变换

方波信号的傅里叶变换
例4―3 求矩形脉冲信号gτ(t)的频谱。
g (t) F()
1
－ 2/
2/
－/ 2 0 / 2
(a)
t
0 (b )

图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6（a）所 示的门函数。其定义为
1 g r (t ) 0 gτ(t)的傅里叶变换为 t t
f (t ) 1

t
F ( j ) 1 e jt dt
单位直流信号的频谱
例4―6 求单位直流信号的频谱。 解 幅度为1的单位直流信号可表示为 f(t)=1,-∞<t<∞ (4―44) 它可以看作是双边指数信号在α取极限趋近0时的一个 特例,即
1 lim e
0
t
u (t ), 0 u( t )] lim[ e
0
t
(4―45)
[1] [lim e
0
t
2a u( t )] lim 2 0 a 2
(4―46)
0 0 0
lim

0
2 2 d lim d( ) 2 2 0 1 ( )2
(4―50)
f (t)
F()
1
0 －1 (a )
t
0

(b )
图4.10 符号函数及其频谱
符号函数sgn(t)也可看作是下述函数在α取极限趋近0时的一 个特例: t e t0 (其中α>0) f ( t ) t t0 e
F [ f (t )]
F(j ) 1
f (t )

方波信号的傅里叶变换_图文

方波信号的傅里叶变换_图文

(4―45)
(4―46)
(4―47)
(4―48) (4―49)
图4.9 单位直流信号及其频谱
符号函数Sgn(t)的频谱函数
例 3.4-7 求符号函数Sgn(t)的频谱函数。
考察例 3.4-4 所示信号f(t)
当α→0时，其极限为符号函数Sgn(t)。因而可以用求f(t)的频 谱函数F(jω)当α→0的极限的方法来求得Sgn(t)的频谱函数。
图 3.8-2 例 3.8-2 (a) 系统组成； (b) s(t)的波形
先求f(t)的傅里叶变换F(jω)，由于
再求s(t)的傅里叶变换S(jω)。由于s(t)为周期信号，T=1ms，则 , 因而有
图 3.8-3 y(t)的求解
图 3.4-4 例 3.4-4 (a) 信号f(t); (b) 频谱
解 图示信号f(t)可表示为
(a>0)
门函数的频谱函数
例 3.4-1 图 3.4-1(a)所示矩形脉冲一般称为门函数。其宽度 为τ， 高度为1，通常用符号gτ(t)来表示。试求其频谱函数。
解 门函数gτ(t)可表示为
Байду номын сангаас
图 3.4-1 (a) 门函数； (b) 门函数的频谱； (c) 幅度谱； (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6（a）所 示的门函数。其定义为
gτ(t)的傅里叶变换为
(4―36)
(4―37) (4―38) (4―39)
δ(t)的频谱函数
例 3.4-5 求单位冲激函数δ(t)的频谱函数。
图 3.4-5 信号δ(t) (a) 单位冲激信号δ(t); (b) δ(t)的频谱

三角波和方波的傅里叶变换公式

三角波和方波的傅里叶变换公式

三角波和方波的傅里叶变换公式
傅里叶变换是一种重要的数学工具，用于将一个函数从时域转
换为频域。

在信号处理和电子工程领域广泛应用。

本文将讨论三
角波和方波的傅里叶变换公式，以便更好地理解它们在频域中的
性质。

首先让我们来看一下三角波的傅里叶变换公式。

三角波是一种
周期函数，其形状类似于直角三角形。

在周期为T的情况下，三
角波可以由一系列正弦函数的叠加来表示。

其傅里叶变换公式为：F(ω) = (2/T) * [sin(ωT/2) / (ω/2)]
其中F(ω)表示频率为ω的频谱成分。

让我们转向方波的傅里叶变换公式。

方波是一种周期为T的函数，其形状为连续的正负矩形脉冲。

同样地，方波也可以由一系
列正弦函数的叠加来表示。

其傅里叶变换公式为：
F(ω) = (4/T) * [sin(ωT/2) / (ω/2)]
根据这个公式，我们可以看到方波相比于三角波有更多的频谱
成分，这是因为方波的形状更接近于理想的方形。

总结一下，三角波和方波的傅里叶变换公式分别为：
三角波：F(ω) = (2/T) * [sin(ωT/2) / (ω/2)]
方波：F(ω) = (4/T) * [sin(ωT/2) /(ω/2)]
这些公式描述了频域中的三角波和方波的性质，为信号处理和
电子工程中的应用提供了重要的数学工具。

通过理解和应用傅里
叶变换，我们可以更好地分析和处理这些周期信号。

方波信号傅里叶变换

方波信号傅里叶变换

例 3.4-4
所示信号的频谱函数为
j
2 2 2
，从而有
Sgn(t) 1
X()
o
t
o
－1
(a) (b)
图 3.4-7 符号函数Sgn(t) (a)Sgn(t)的波形； (b) 频谱
符号函数的频谱
例4―7求符号函数的频谱。 解 符号函数简记为sgn(t),它的定义为
1 t 0 sgn(t) 0 t 0 1 t 0
(b)
图 3.4-2 单边指数函数e-αt
(a) 单边指数函数e-αt; (b) e-αt的幅度谱
解
F(j) f(t)ejtdt etejtdt
e(j)t
(j)
01j
1
jarctan
ea
a22
其振幅频谱及相位频谱分别为
F ( ) 1 2 2
( ) arctan
单边指数信号的频谱
－ 30°
－ 20°
－ 30°
－ 45°
－ 45° (b )
图 3.3-2 例 3.3-1 信号的 (a) 振幅谱； (b) 相位谱
单边指数函数f(t)的频谱函数
例 3.4-2 求指数函数f(t)的频谱函数。
f
(t)
e at
t 0
0
t 0
f (t)
1 e－t (＞0)
(0)
F()
1
o
t
o
(a)
fo (t)
e a t
e
a
t
t0 t0
Fe()
et
ejt
0
e(j)tdt
0
e(j)tdt 222
Fo()
0

方波的傅里叶级数关系方程

方波的傅里叶级数关系方程

方波的傅里叶级数关系方程
方波的傅里叶级数是一种周期为T的函数，在周期内可表示为无穷级数的形式。

根据傅里叶级数的定义，方波的傅里叶级数可以表示为以下公式：
f(x) = (4/π) * [sin(πx/T) + (1/3)sin(3πx/T) + (1/5)sin(5πx/T) + ...]
其中，f(x)为方波函数，x为自变量，T为周期。

可以看出，方波的傅里叶级数是由一系列正弦函数组成的，每个正弦函数的振幅和频率都不同。

这些正弦函数的频率是方波函数基频的整数倍，即基频的1倍、3倍、5倍等。

振幅则是基频振幅的1/1、1/3、1/5等。

如果将上述公式中每一项的系数表示出来，就可以得到方波的傅里叶级数关系方程：
a0 = 0
an = (4/T) * [(-1)^n - 1]/πn , n为奇数
bn = 0 , n为偶数
其中，a0表示傅里叶级数中的直流分量，an和bn分别表示傅里叶级数中的正弦项和余弦项的系数。

这些系数是根据傅里叶级数的公式和基频为1/T的正弦函数的特点计算得出的。

方波的傅里叶级数关系方程可以帮助我们更好地理解方波的傅
里叶级数的特点和性质，也可以用于计算方波函数的傅里叶级数分解。

- 1 -。

方波信号的傅里叶变换

方波信号的傅里叶变换

信号的滤波
滤波器设计
通过傅里叶变换，可以将信号分解为 不同频率的分量，从而根据需要设计 滤波器，滤除特定频率范围的分量。
噪声抑制
在信号中混入噪声时，傅里叶变换可 以帮助识别和分离噪声分量，从而降 低噪声对信号的影响。
信号的压缩与扩展
压缩编码
通过对方波信号进行傅里叶变换，可 以将信号压缩为较小的数据量，便于 存储和传输。
方波信号的性质
01
方波信号具有明确的频率成分，其傅里叶变换可以 解析为简单的正弦和余弦函数。
02
方波信号的频率成分与其周期T有关，可以通过傅里 叶变换得到。
03
方波信号的波形因子a决定了其频谱的宽度和峰值。
方波信号的应用
1
方波信号在通信、控制、测量等领域有广泛应用 。
2
方波信号可以用于产生电磁波、调制载波等。
方波的频谱幅度随着谐波次数增 加而减小，呈现快速衰减的趋势 。
方波信号的频域特性周期性来自方波信号在频域内表现为一系列离散的谐波分量，这 些分量具有周期性重复的特点。
带宽有限
方波信号的频域特性表明其带宽是有限的，即其最高 频率分量是有限的。
能量集中
方波信号的能量主要集中在基频和较低次谐波上，高 次谐波携带的能量逐渐减少。
3
方波信号在数字电路中常被用作时钟信号。
02
CATALOGUE
傅里叶变换基础
傅里叶变换的定义
01
傅里叶变换是一种将时域信号转换为频域信号的方法。
02
对于给定的时域信号，通过傅里叶变换，可以得到该信号的频
谱。
傅里叶变换的基本公式为：(X(f) = int_{-infty}^{infty} x(t)
方波信号的傅里叶变换

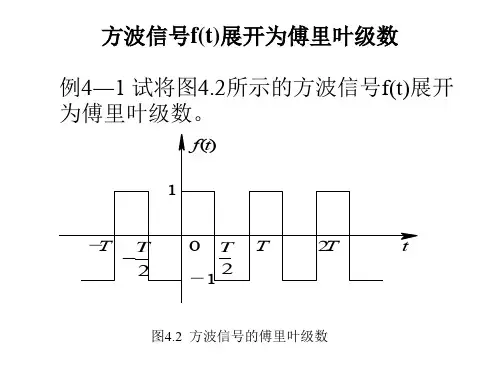
方波信号f(t)展开为傅里叶级数


0.4 0.2
－ 6－ 5 － 4－ 3－ 2 － o
2 3 4 5 6
(a )
n 45 °
45 °
30 ° 30 °
20 °
15° 10°
－ 6－ 5 － 4－ 3 － 2 － o
2 3 4 5 6
－ 10° － 15°
－ 30°
－ 20°
－ 30°
－ 45°
－ 45° (b )
图 3.3-2 例 3.3-1 信号的 (a) 振幅谱； (b) 相位谱
例4―11 已知
gr(t)Sa(2)
求gτ(2t)的频谱函数 解 根据傅里叶变换的尺度变换性
质,gτ(2t)的频谱函数为
[gr(2t)]1 2Sa( 4 )
f (t) 1
0
t
22
f (2t)
1
0
t
44
F()
2π
2π
0
1 F()
22
4π
4π
0
图4.13 尺度变换
利用奇偶虚实性求频谱
例4―9利用奇偶虚实性求图4.11单边指数信 号f(t)=2e-αt u(t)的频谱。
F() (t)ejtdt1
(t)1
(4―34) (4―35)
(t)
(1)
0 (a)
F()
1
t
0
(b)
图4.5 冲激信号及其频谱
移位冲激函数δ(t-t0)的频谱函数
例4―12求移位冲激函数δ(t-t0)的频谱函数。
解 由于已知冲激函数δ(t)的频谱函数为1, 求移位冲激函数δ(t-t0)的频谱函数，此时可利 用傅里叶变换的时移特性式(4―74)。
(4―45) (4―46)

方波信号的傅里叶变换课件

通过计算信号与三角函数系中各个函数的内积，得到傅里叶系数，从而确定各 个分量的幅值和相位。
奇偶函数展开特点
奇函数展开
奇函数展开后只包含正弦项，不包含余弦项和直流分量。
偶函数展开
偶函数展开后只包含余弦项和直流分量，不包含正弦项。
04
方波信号的傅里叶级数展开
奇偶方波信号展开过程
奇偶性判断
首先要判断方波信号是奇函数还是偶函数，或者是非奇非偶函数。奇函数和偶函数具有不 同的傅里叶级数展开形式。
周期
方波信号的周期是指信号重复出现的最小时间间隔，用T 表示，单位为秒（s）。
频率
方波信号的频率是指单位时间内信号重复出现的次数，用 f表示，单位为赫兹（Hz），与周期互为倒数关系，即 f=1/T。
占空比
方波信号的占空比是指在一个周期内高电平持续时间与周 期之比，通常用百分比表示。占空比越大，高电平持续时 间越长，反之则越短。
方波信号分类
单极性方波
单极性方波信号的高电平为正值，低 电平为零。这种信号通常用于数字电 路中，表示二进制数的“0”和 “1”。
双极性方波
双极性方波信号的高电平和低电平分 别为正负两个值，且绝对值相等。这 种信号通常用于模拟电路中，可以表 示交流信号的正负变化。
03
傅里叶级数展开原理
三角函数系正交性
号在各个频率上的分量。
线性性质
若信号在时域中满足线性叠加 原理，则其傅里叶变换在频域
中也满足线性叠加原理。
时移性质
信号在时域中的时移对应于其 傅里叶变换在频域中的相移。
频移性质
信号在时域中的频率变化对应 于其傅里叶变换在频域中的位
置变化。
常见函数傅里叶变换对
正弦函数与余弦函数

方波信号傅里叶变换

从频谱函数的定义式出发
F()0 eat
ejtdt0 eat
ejtdt1j1j
22 2
(4―43)
f (t) 1
0
t
(a)
F()
2
1
－ 0
(b)
图4.8 双边指数信号及其频谱
奇对称双边指数函数的频谱函数
例 3.4-4 求图 3.4-4(a)所示信号f(t)的频谱函数。
f(t) 1
e－t ＞0)
例4―3 求矩形脉冲信号gτ(t)的频谱。
g(t)
F()
1
－ 2/
2/
－/ 2 0 / 2
t
(a)
0
(b)
图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6（a）所 示的门函数。其定义为
g r (t)
1
0
t 2
t 2
gτ(t)的傅里叶变换为
[ g r (t)]
2
A2 2
1 0 1 10 2 20
A3 0.4
3 45
A6 0.8
6 30
其余 An 0
An 3 3
2 2
1
0.8
0.4
o
2 3 4 5 6
(a )
n
45 °
45 °
30 ° 30 °
20 °
15 °
10 °
o
2
3
4
5
6
(b )
图 3.3-1 例 3.3-1
例 3.4-3 求图 3.4-3(a)所示双边指数函数的频谱函数。
f (t)
1
et
e－t ＞0)
o

matlab方波傅里叶变换

Matlab方波傅里叶变换1. 引言傅里叶变换是一种重要的数学工具，用于将一个信号从时域转换到频域。

在Matlab中，我们可以使用内置的函数来执行傅里叶变换和逆傅里叶变换。

本文将介绍如何使用Matlab进行方波的傅里叶变换，并分析其频谱特性。

2. 方波信号的定义方波是一种特殊的周期信号，其波形为由两个不同幅值的水平线段组成的周期函数。

方波的周期为T，幅值为A和-B。

在Matlab中，我们可以使用以下代码定义一个方波信号：T = 1; % 周期A = 1; % 正半幅值B = -1; % 负半幅值t = linspace(0, 4*T, 1000); % 时间向量x = A*square(2*pi/T*t, 50) - B; % 方波信号上述代码中，我们使用了Matlab的linspace函数生成一个包含1000个元素的时间向量t，范围从0到4倍周期T。

然后，我们使用square函数生成一个周期为2*pi的方波信号，其中50表示方波的占空比为50%。

最后，我们通过乘以幅值A和B的差来将方波信号归一化。

3. 傅里叶变换在Matlab中，我们可以使用fft函数对方波信号进行傅里叶变换。

傅里叶变换将信号从时域转换到频域，得到信号的频谱信息。

N = length(x); % 信号长度Fs = N / (4*T); % 采样频率f = (-Fs/2 : Fs/N : Fs/2 - Fs/N); % 频率向量X = fftshift(fft(x)); % 傅里叶变换上述代码中，N表示信号的长度，Fs表示采样频率，f表示频率向量，X表示傅里叶变换后的信号。

我们使用fftshift函数将频谱移动到中心位置，以便更好地观察频谱特性。

4. 频谱分析通过对方波信号进行傅里叶变换，我们可以得到其频谱信息。

频谱图显示了信号在不同频率上的幅度。

figure;plot(f, abs(X)/N);xlabel('Frequency (Hz)');ylabel('Amplitude');title('Frequency Spectrum');上述代码中，我们使用plot函数绘制频谱图，其中横轴表示频率，纵轴表示幅度。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

偶对称双边指数信号的频谱
例4―5 求双边指数信号的频谱。 解 双边指数信号是指
f (t) e t u(t), 0
从频谱函数的定义式出发
(4―42)
F ( ) 0 eat ge jtdt 0 eat ge jtdt 1 1
j j
2 2
2
(4―43)
f (t) 1
0
t
(a)
n )
可知，其基波频率Ω=π(rad/s)，基本周期T=2 s，ω=2π、3π、 6 π分别为二、 三、六次谐波频率。且有
A0 1 2 A1 3
A2 2
1 0 1 10 2 20
A3 0.4
3 45
A6 0.8
6 30
其余 An 0
An 3 3
2 2
1
0.8
0.4
o 2 3 4 5 6
例 3.3-1 f (t) 1 3cos(t 10) 2 cos(2t 20)
0.4 cos(3t 45) 0.8cos(6t 30),
试画出f(t)的振幅谱和相位谱。
解 f(t)为周期信号，题中所给的f(t)表达式可视为f(t)的傅里
叶级数展开式。据
f
(t)
A0 2
n1
An cos(nt
[
g
r
(t
)]
Sa
(
2
)
(4―36)
(4―37) (4―38) (4―39)
δ(t)的频谱函数
例 3.4-5 求单位冲激函数δ(t)的频谱函数。
f(t)
F(j )
1
(t)
o
t
(a)
o
(b)
图 3.4-5 信号δ(t) (a) 单位冲激信号δ(t); (b) δ(t)的频谱
解
方波信号的傅里叶变换
解 我们将信号按式(4―6)分解成傅里叶级数,
并按式(4 及c。
―
7)、(4―8)、(4―9)分别计算an,
bn
an
2 T
T
2 T
2
f (t) cos(2 nft)dt
2
T
0 T
2
(1) cos(2 nft)dt 2
T
T 2 0
1gcos(2 nft)dt2 T12 nf
f
(t)
eat
t0
0
t0
f (t)
1 e－t ( ＞ 0)
( 0)
F( )
1
o
t
o
(a)
(b)
图 3.4-2 单边指数函数e-αt
(a) 单边指数函数e-αt; (b) e-αt的幅度谱
解
F ( j ) f (t)e jtdt ete jtdt
e( j )t
( j)
0
1
j
g(t)
F()
1
－ 2/
2/
－/ 2 0 / 2
t
(a)
0
(b)
图4.6 矩形脉冲信号及其频谱
解 矩形脉冲信号gτ(t)是一个如图4.6（a）所 示的门函数。其定义为
gr
(t)
1
0
t
2
t
2
gτ(t)的傅里叶变换为
[gr (t)]
2 2
e jtdt sin( / 2) / 2
Sa(x) sin(x) x
F ( )
2
1
－ 0
(b)
图4.8 双边指数信号及其频谱
奇对称双边指数函数的频谱函数
例 3.4-4 求图 3.4-4(a)所示信号f(t)的频谱函数。
f(t) 1
e－t ＞0)
X( )
1
o
t
－ et
o
－1 (a)
图 3.4-4 例 3.4-4 (a) 信号f(t); (b) 频谱
－
1
(b)
解 图示信号f(t)可表示为
1
j arctan
e
a
a2 2
其振幅频谱及相位频谱分别为
F ( ) 1 2 2
( ) arctan
单边指数信号的频谱
例4―4 求单边指数信号的频谱。 解 单边指数信号是指
f (t) eatu(t), a 0
F ( ) f (t)e jtdt eat ge jtdt
1
j
[ cos(2 nft)]
T
2 0
2 (1 n ) n
0,
4
n
n 2, 4,6, n 1,3,5,
c 2 T
T
2 T
2
f (t)dt 0
f (t) 4 [sin 2 ft 1 sin 6 ft 1 sin10 f 1 sin 2 ft ]
3
5
n
n 1,3,5,
振幅谱和相位谱例题
g(t) 1
－τ2o
τ 2
t
(a)
F(j )
2
－4 －2 o
4
(b)
F( )
( )
－ 4
－
2
o
2 4
－4
－
2
o 2 4
－
(c)
(d)
图 3.4-1 (a) 门函数； (b) 门函数的频谱； (c) 幅度谱； (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
f
(t)
eat
eat
t0
(a>0)
t0
F ( j ) 0 eate jtdt ete jtdt
0
1
j
1
j
j
a2
2
2
门函数的频谱函数
例 3.4-1 图 3.4-1(a)所示矩形脉冲一般称为门函数。其宽度 为τ， 高度为1，通常用符号gτ(t)来表示。试求其频谱函数。
解 门函数gτ(t)可表示为
[ sin(2 nft)]
0 T
2
2 T
1
2 nf
[sin(2 nft)]
T
2 0
0
bn
2 T
T
2 T
2
f (t)sin(2 nft)dt
2 T
0 T
2
(1)sin(2 nft)dt 2
T
T 2 0
1gsin(2 nft)dt
2 T
1
2 nft
[ cos(2 nft)]
0 T
2
2 T
1
2 nf
0
(4―40) (4―41)
F ( )
1
12
－ 0
(a)
argF()
2
4
－ 0
－
4
－
2
(b)
图4.7 单边指数信号及其频谱
偶对称双边指数函数的频谱函数
例 3.4-3 求图 3.4-3(a)所示双边指数函数的频谱函数。
f (t)
1
et
e－t ＞0)
o
t
(a)
F(j )
2
o
(b)
图 3.4-3 (a) 双边指数函数； (b) 频谱
(a)
n 45 °
45 °
30 ° 30 °
20 °
15° 10°
o
2
3
4
5
6
(b)
图 3.3-1 例 3.3-1
(a) 振幅谱； (b) 相位谱
|F n |
2
1.5
1.5
1
1
1
0.4 0.2
0.4 0.2
－ 6－ 5 － 4－ 3－ 2 － o 2 3 4 5 6
(a)
n 45 °
45 °
30 ° 30 °
20 °
15° 10°
－ 6－ 5 － 4－ 3－ 2 － o
2 3 4 5 6
－ 10° － 15°
－ 30°
－ 20°
－ 30°
－ 45°
－ 45° (b)
图 3.3-2 例 3.3-1 信号的 (a) 振幅谱； (b) 相位谱
单边指数函数f(t)的频谱函数
例 3.4-2 求指数函数f(t)的频谱函数。