傅里叶变换的基本概念及基本定理
- 格式:ppt
- 大小:727.00 KB
- 文档页数:37
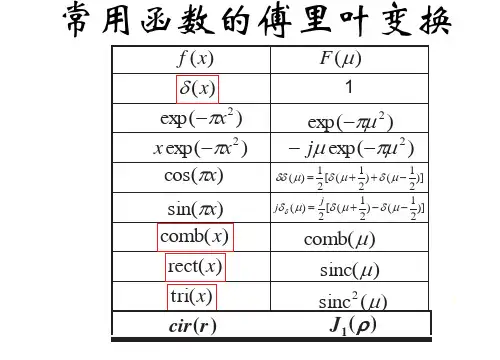


傅里叶变换的基本原理傅里叶变换是一种将一个函数(在时间或空间域)转变为频域表达的数学工具。
它常用于信号处理、图像处理以及物理学中。
傅里叶变换可以将一个连续时间域的函数转换为一个连续频率域的函数,或者将一个离散时间域的序列转换为一个离散频率域的序列。
傅里叶变换的基本原理是基于一个重要的数学定理,即任何连续函数都可以表示为无穷多个正弦和余弦函数的和。
这个数学定理称为傅里叶级数展开。
根据傅里叶级数展开定理,我们可以利用一组基函数来表示一个函数,这组基函数由正弦和余弦函数构成,具有不同的频率和振幅。
在实际应用中,傅里叶变换通过将一个函数分解成各种频率的正弦和余弦函数的和来分析该函数的频谱。
傅里叶变换将原始函数转换为一个频谱图,其中横轴表示不同的频率,纵轴表示每个频率分量的强度。
通过分析频谱图,我们可以获得原始函数的频率成分信息,例如哪些频率分量更强或更弱,进而帮助我们理解信号或图像的特征。
傅里叶变换的数学表达式是通过将原始函数与一组复指数函数进行内积的方式定义的。
具体来说,傅里叶变换将原始函数f(x)变换为F(k),其中k表示频率。
傅里叶变换可以表示为以下公式:F(k) = ∫[e^(-2πikx)] * f(x) dx这里的e表示自然对数的底(欧拉数),i表示虚数单位。
该公式中的积分描述了原始函数f(x)与每个频率分量e^(-2πikx)之间的相互作用。
傅里叶变换的逆变换即将频率域的函数转换为时间或空间域的函数。
逆变换可以表示为以下公式:f(x) = ∫[e^(2πikx)] * F(k) dk这个公式与傅里叶变换公式非常相似,只是其中的积分方向相反。
傅里叶变换在信号处理中有着广泛的应用。
它可以用于滤波、图像压缩、频谱分析等方面。
通过傅里叶变换,我们可以提取信号或图像中的特定频率成分,并对其进行处理或分析。
傅里叶变换的基本原理为信号处理和频谱分析提供了强大的数学工具,对于数字信号处理和数字图像处理有着重要的作用。


傅里叶变换的基本性质和应用傅里叶变换,是20世纪初法国数学家傅里叶的发明,是将一个时间函数或空间函数的复杂波形分解成一系列简单的正弦波的工具。
它是信号处理和图像处理领域非常重要的一种数学变换,广泛应用于通信、图像、音频等领域。
一、傅里叶变换的基本概念傅里叶变换是一种将时域信号(即关于时间的函数)转换为频域信号(即关于频率的函数)的数学工具。
在时域中,信号可以表示为一个随着时间变化而变化的函数;在频域中,信号可以表示为它的频谱分布,即各个频率成分的大小。
傅里叶变换是互逆的,也就是说,将一样以频率表示的信号进过傅里叶逆变换,可以得到原始的时域信号。
傅里叶变换和傅里叶逆变换的基本公式分别如下:$$ F(\omega) = \int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt $$$$ f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty}F(\omega)e^{i\omega t}d\omega $$其中,$f(t)$ 是时域信号,$F(\omega)$ 是频域信号,$\omega$ 是角频率。
傅里叶变换可以看作一种基变换,将时域信号换到频域进行分析,从而可以更好地理解信号的性质。
二、傅里叶变换的基本性质1. 线性性质傅里叶变换是线性的,即对于一个常数乘以一个时域信号进行傅里叶变换,等价于将该常数乘以该信号的傅里叶变换。
即:$$ F(cf(t)) = cF(f(t)) $$其中,$c$ 是常数。
此外,傅里叶变换具有加权叠加的特性,也就是说,将两个时域信号求和再进行傅里叶变换,等价于分别对这两个信号进行傅里叶变换后再相加。
即:$$ F(f(t) + g(t)) = F(f(t)) + F(g(t)) $$2. 时移性质傅里叶变换具有时移性质,也就是说,在时域中将一个信号向右或向左平移 $\tau$ 个单位,它的傅里叶变换相位也会相应发生$\tau$ 的变化。

傅里叶变换常用公式大全傅里叶变换是一种重要的数学工具,用于将信号从时域转换到频域。
在信号处理、图像处理和通信领域广泛应用。
本文将介绍一些傅里叶变换中常用的公式,以帮助读者更好地理解和应用傅里叶变换。
1. 傅里叶变换的定义公式傅里叶变换的定义公式如下:F(ω) = ∫[f(t) * e^(-jωt)]dt其中F(ω)表示信号f(t)在频率ω处的傅里叶变换。
2. 傅里叶变换的逆变换公式傅里叶变换的逆变换公式如下:f(t) = ∫[F(ω) * e^(jωt)]dω其中f(t)表示频域信号F(ω)的逆变换。
3. 傅里叶级数展开公式傅里叶级数展开公式将一个周期信号表示为一系列正弦和余弦函数的和。
公式如下:f(t) = a₀ + Σ[aₙ * cos(nω₀t) + bₙ * sin(nω₀t)]其中a₀, aₙ, bₙ为系数,n为正整数,ω₀为基本角频率。
4. 傅里叶级数系数计算公式傅里叶级数系数的计算公式如下:a₀ = 1/T₀ * ∫[f(t)]dtaₙ = 2/T₀ * ∫[f(t) * cos(nω₀t)]dtbₙ = 2/T₀ * ∫[f(t) * sin(nω₀t)]dt其中T₀为周期。
5. 傅里叶变换的线性性质公式傅里叶变换具有线性性质,公式如下:F(a * f(t) + b * g(t)) = a * F(f(t)) + b * F(g(t))其中a和b为常数。
6. 傅里叶变换的频移性质公式傅里叶变换具有频移性质,公式如下:F(f(t - t₀)) = e^(-jωt₀) * F(f(t))其中t₀为时间偏移量。
7. 傅里叶变换的频率缩放公式傅里叶变换具有频率缩放性质,公式如下:F(f(a * t)) = (1/|a|) * F(f(t/a))其中a为常数。
8. 傅里叶变换的频域微分公式傅里叶变换的频域微分公式如下:F(d/dt[f(t)]) = jωF(f(t))其中d/dt表示对时间t的导数。




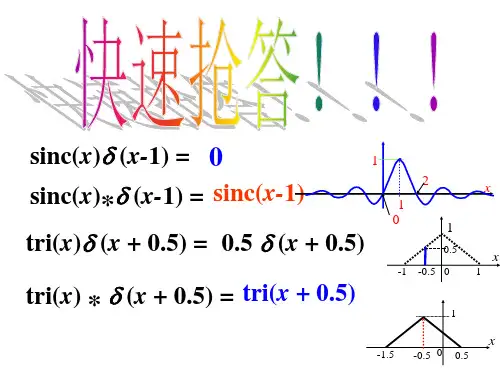
傅里叶变换及其在信号处理中的应用傅里叶变换是一种非常常见的数学变换,也是信号处理中非常重要的技术。
它在很多领域都有广泛的应用,如音频和视频压缩、图像处理、信号滤波、模拟信号的数字化和数字信号的合成等等。
本文将介绍傅里叶变换的基本概念、性质和应用,旨在为读者提供一个较全面的了解。
一、傅里叶变换的基本概念傅里叶变换是一种将时间域信号或空间域信号转换为频域信号的数学工具。
它是一种线性可逆变换,假设f(t)是一个时间域信号,则它的复数形式的傅里叶变换F(ω)可以表示为:F(ω) = ∫ f(t) e^(-jωt) dt其中,ω是频率,e^(-jωt)是一个复指数,表示随时间推移,相位角度为-ωt的旋转矢量。
这里需要说明,ω通常被定义为角频率,因此在正交坐标系中,实际传输的是该信号的实部和虚部的两组信号,常用AFWT算法。
二、傅里叶变换的性质傅里叶变换有许多非常重要的性质,这里简单介绍其中一些:1. 线性性:傅里叶变换是线性可逆变换,能够满足线性叠加的性质,即:F (af(t) + bg(t)) = aF(f(t)) + bF(g(t))其中,a和b是任意常数,f(t)和g(t)是任意两个时间域信号。
2. 分解定理:对于一个周期性信号,它可以用一系列正弦和余弦函数的和表示。
这个定理反过来也成立,即,任何一个信号都可以用一系列正弦和余弦函数的和表示。
3. 能量守恒:傅里叶变换维持了信号的能量守恒,并且将信号对应到不同的频率成分上,进行频谱分析。
三、傅里叶变换的应用傅里叶变换在信号处理中有着广泛的应用,下面简要介绍一些应用:1. 音频和视频压缩:在将音频和视频信号压缩成较小的文件时,傅里叶变换是非常重要的。
通过傅里叶变换,信号可以从时间域转换到频率域,并且可以通过滤波和降低频率分辨率等方式来压缩信号。
这样,在保证一定的信号质量的前提下,就可以将信号文件大小降低到较小程度。
2. 图像处理:在图像处理中,傅里叶变换的主要作用是在频率域对图像进行滤波和增强。
关于傅立叶变换,无论是书本还是在网上可以很容易找到关于傅立叶变换的描述,但是大都是些故弄玄虚的文章,太过抽象,尽是一些让人看了就望而生畏的公式的罗列,让人很难能够从感性上得到理解,最近,我偶尔从网上看到一个关于数字信号处理的电子书籍,是一个叫Steven W. Smith, Ph.D.外国人写的,写得非常浅显,里面有七章由浅入深地专门讲述关于离散信号的傅立叶变换,虽然是英文文档,我还是硬着头皮看完了有关傅立叶变换的有关内容,看了有茅塞顿开的感觉,在此把我从中得到的理解拿出来跟大家分享,希望很多被傅立叶变换迷惑的朋友能够得到一点启发,这电子书籍是免费的,有兴趣的朋友也可以从网上下载下来看一下,URL地址是:/pdfbook.htm要理解傅立叶变换,确实需要一定的耐心,别一下子想着傅立叶变换是怎么变换的,当然,也需要一定的高等数学基础,最基本的是级数变换,其中傅立叶级数变换是傅立叶变换的基础公式。
二、傅立叶变换的提出让我们先看看为什么会有傅立叶变换?傅立叶是一位法国数学家和物理学家的名字,英语原名是Jean Baptiste Joseph Fourier(1768-1830), Fourier对热传递很感兴趣,于1807年在法国科学学会上发表了一篇论文,运用正弦曲线来描述温度分布,论文里有个在当时具有争议性的决断:任何连续周期信号可以由一组适当的正弦曲线组合而成。
当时审查这个论文的人,其中有两位是历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827),当拉普拉斯和其它审查者投票通过并要发表这个论文时,拉格朗日坚决反对,在近50年的时间里,拉格朗日坚持认为傅立叶的方法无法表示带有棱角的信号,如在方波中出现非连续变化斜率。
法国科学学会屈服于拉格朗日的威望,拒绝了傅立叶的工作,幸运的是,傅立叶还有其它事情可忙,他参加了政治运动,随拿破仑远征埃及,法国大革命后因会被推上断头台而一直在逃避。
一、傅里叶变换1、傅里叶积分存在定理:设()f t 定义在(),-∞+∞内满足条件:1)()f t 在任一有限区间上满足狄氏条件; 2)()f t 在(),-∞+∞上绝对可积(即()f t dt +∞-∞⎰收敛;则傅氏积分公式存在,且有()()()()()(),1[]11002,2iw iwt f t t f t f e d e dw f t f t t f t τττπ+∞+∞--∞-∞⎧⎪=-⎨++-⎪⎩⎰⎰是的连续点是的第一类间断点2、傅里叶变换定义式:()[]()()iwt F f t F w f t e dt +∞--∞==⎰ 1-2 傅里叶逆变换定义式:()11[]()()2iwt F F w f t F w e dw π+∞--∞==⎰1-33、常用函数的傅里叶变换公式()1()FFf t F ω-−−→←−− 矩形脉冲函数1,22()sin 20,2F F E t E f t t ττωτω-⎧≤⎪⎪−−→=⎨←−−⎪>⎪⎩1-4 单边指数衰减函数()()1,0110,0tFFe t e t F e t iw j t βββω--⎧≥−−→=⇒=⎡⎤⎨←−−⎣⎦++<⎩ 1-5 单位脉冲函数 ()11FF t δ-−−→←−− 1-6 单位阶跃函数 ()()11FFu t w iwπδ-−−→+←−− 1-7 ()112F Fw πδ-−−→←−− 1-8 ()12F Ft j πδω-−−→'←−− 1-9 ()0102F j t Fe ωπδωω-−−→-←−− 1-10 ()()1000cos F Ft ωπδωωδωω-−−→++-⎡⎤←−−⎣⎦1-11 ()()1000sin F Ft j ωπδωωδωω-−−→+--⎡⎤←−−⎣⎦1-12 4、傅里叶变换的性质设()()[]F f t F w =, ()()[]i i F f t F w =(1)线性性:()()1121()()FFf t f t F F αβαωβω-−−→++←−− 1-13 (2)位移性:()()010Fj t Ff t t e F ωω--−−→-←−− 1-14 ()010()F j t Fe f t F ωωω-−−→-←−− 1-15 (3)微分性:()1()FFf t j F ωω-−−→'←−− 1-16 ()()()1()Fnn Ff t j F ωω-−−→←−− 1-17 ()()1()FFjt f t F ω-−−→'-←−− 1-18 ()()()()1()Fn n Fjt f t F ω-−−→-←−− 1-19 (4)积分性:()11()tFFf t dt F j ωω--∞−−→←−−⎰ 1-20 (5)相似性:11()FFf at F a a ω-⎛⎫−−→←−− ⎪⎝⎭1-21 (6)对称性:()1()2FFF t f πω-−−→-←−− 1-22 上面性质写成变换式如下面:(1)线性性:[]1212()()()()F f t f t F w F w αβαβ⋅+⋅=⋅+⋅ 1-13-1[]11212()()()()F F w F w f t f t αβαβ-⋅+⋅=⋅+⋅(,αβ是常数)1-13-2(2)位移性:[]0()F f t t -=()0iwt e F w - 1-14()000()()iw tw w w F e f t F w F w w =-⎡⎤==-⎣⎦ 1-15(3)微分性:设+∞→t 时,0→)t (f , 则有[]()()()()[]()F f t iw F f t iw F w '== 1-16()()()()()[]()nn n F f t iw F f t iw F w ⎡⎤==⎣⎦1-17 []()()dF tf t jF w dw= 1-18 ()()nnnn d F t f t j F w dw ⎡⎤=⎣⎦ 1-19(4)积分性:()()t F w F f t dt iw-∞⎡⎤=⎢⎥⎣⎦⎰ 1-20(5)相似性:[]1()()wF f at F a a=1-21-1 翻转性:1=a 时()()w F t f F -=-][ 1-21-2 (6)对称性:设 ()()w F t f −→←,则()()w f t F π2−→←- 或 ()()2F t f w π←−→- 1-225、卷积公式 :)()(21t f t f *=τττd t f f )()(21-⎰+∞∞-。
傅里叶变换的定义及基本概念
傅里叶变换是一种能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合的方法。
它可以在不同的研究领域中,如数字信号处理、热过程的解析分析等中,有不同的变体形式,如连续傅里叶变换和离散傅里叶变换。
傅里叶变换的定义和基本概念如下:
傅里叶变换的基本性质:包括对称性质、奇偶性质、线性性质、时移性质、频移性质、尺度变换性质、卷积定理、时域微积分等。
傅里叶变换的收敛性:在一个周期内具有有限个极值点,绝对可积。
傅里叶变换的充要条件:函数在xoy全平面上绝对可积,即函数在xoy全平面上每一个有限区域内局部连续,仅存在有限个间断点;函数没有无限大间断点。
广义傅里叶变换:对于某些无法满足存在条件的函数,如sgn(x)、step(x)、三角函数、脉冲函数等,需要推广傅里叶变换的定义,即广义傅里叶变换。
第三章 傅里叶变换一.周期信号的傅里叶级数知 识 要 点1、 周期信号的傅里叶级数任一满足狄利克雷条件的周期信号()f t (1T 为其周期)可展开为傅里叶级数。
(1)三角函数形式的傅里叶级数 0111()[cos()sin()]nn n f t a an t b n t ωω∞==++∑式中112T πω=,n 为正整数。
直流分量010011()t T t a f t dt T +=⎰ 余弦分量的幅度010112()cos()t T t a f t n t dt T ω+=⎰正弦分量的幅度01112()sin()t T n t b f t n t dt T ω+=⎰ 三角函数形式的傅里叶级数的另一种形式为011()cos()nn n f t c cn t ωϕ∞==++∑频谱:离散性、谐波性、收敛性或011()sin()nn n f t d dn t ωϑ∞==++∑以上几种表示形式中各个量之间的关系为000a c d ==n n c d ==cos sin n n n n n a c d ϕϑ== sin cos n n n n n b c d ϕϑ=-=tan nn n a b ϑ=tan nn na b ϕ=-(1,2,)n =,,n n n a c d 为1n ω的偶函数,,,n n n b ϕϑ为1n ω的奇函数。
(2)指数形式的傅里叶级数11()()jn tn f t F n eωω∞=-∞=∑式中,n 为从-∞到+∞的整数。
复数频谱0110111()()t T jn tn t F F n f t e dt T ωω+-==⎰n F 与其他系数之间的关系为 0000F c d a ===1()2n j n n n n F F c a jb ϕ==-1()2n j n n n n F F c a jb ϕ---==+1122n n n n F F c d -====n n n F F a -+=n n n F F c -+=()n n n b j F F -=-n F 是1n ω的偶函数。