方波信号的傅里叶变换_图文
- 格式:pptx
- 大小:5.01 MB
- 文档页数:80


方波傅里叶变换在信号处理中,傅里叶变换是一种重要的数学工具,用于将一个信号分解为其频谱成分。
而方波傅里叶变换则是傅里叶变换的一种特殊形式,用于分析方波信号的频谱特性。
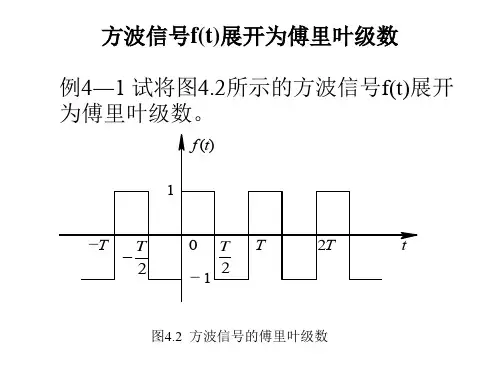
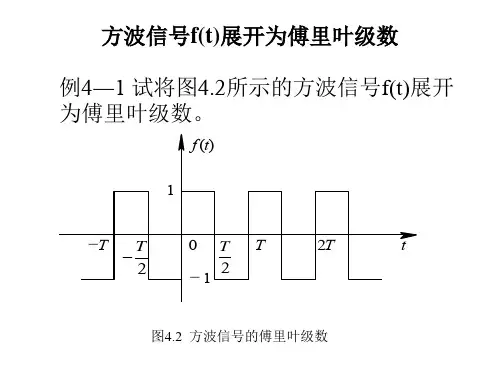
方波是一种典型的周期信号,其波形呈现出由高电平和低电平交替组成的矩形形状。
方波信号在数字电路和通信系统中广泛应用,因其简单明了的特点,能够有效地携带和传输信息。
傅里叶变换通过将一个信号分解为一系列正弦和余弦函数的叠加,将信号从时域转换到频域。
对于方波信号而言,傅里叶变换能够揭示其频谱特性,即方波信号中包含的各个频率成分。
方波信号的频谱图呈现出一系列垂直的频谱线,这些频谱线对应着方波信号中不同的频率成分。
方波信号的频率谱是离散的,且只包含奇次谐波。
由于方波信号是一个周期为T的信号,其频谱中的频率成分由基波频率和其奇次谐波频率构成。
在方波信号的频谱中,基波频率对应着方波信号的周期,即1/T。
而奇次谐波频率则是基波频率的整数倍。
这意味着方波信号的频谱中只包含了奇次谐波成分,如3倍频、5倍频等。
方波傅里叶变换的结果可以用于分析方波信号的频谱特性,从而了解信号中包含的各个频率成分。
通过傅里叶变换,我们可以得到方波信号的频率谱图,进而分析信号的频谱分布和能量分布。
方波傅里叶变换在实际应用中有着广泛的应用。
例如,在通信系统中,方波信号被广泛应用于数字调制和解调、编码和解码等方面。
通过对方波信号的频谱分析,可以了解信号的频率特性,从而设计合适的调制和解调方式,实现高效的数据传输。
方波傅里叶变换还在数字电路设计中起着重要的作用。
在数字电路中,方波信号被用作时钟信号,用于同步和控制电路的工作。
通过对方波信号的频谱分析,可以确定时钟信号的频率范围,从而确保电路的正常工作。
方波傅里叶变换是一种用于分析方波信号频谱特性的重要工具。
通过傅里叶变换,我们可以了解方波信号中包含的各个频率成分,从而在信号处理、通信系统和数字电路设计等领域中应用。
方波傅里叶变换的研究和应用将进一步推动信号处理技术的发展,并为实际应用带来更多的创新和改进。

傅里叶变换正弦波分解方波傅里叶变换是一种非常重要的数学工具,可以将一个信号分解成不同频率的正弦波的叠加。
而其中一种特殊的信号,方波,可以通过傅里叶变换来进行分解和理解。
正弦波是一个周期性的波形,具有不同的频率和振幅。
傅里叶变换可以将任意一个周期性的信号分解成多个正弦波。
这是因为正弦波具有唯一的频率,可以表示任意周期性信号的一个重要组成部分。
通过傅里叶变换,我们可以知道一个信号包含哪些频率的正弦波,以及每个正弦波的振幅。
方波是一种非常特殊的波形,它在每个周期内都有两个不同的振幅值。
在傅里叶变换中,方波可以看作是多个正弦波的叠加。
具体地说,一个方波信号可以拆解成一个基频为f的正弦波和其奇数倍频的正弦波的叠加。
这是因为方波信号的周期性导致其可以用不同频率的正弦波分解。
通过傅里叶变换分解方波信号,我们可以得到其包含的不同频率的正弦波,并且可以知道每个正弦波的振幅。
这种分解和分析的方法非常有意义。
首先,我们可以了解方波信号的频率组成成分,进一步理解信号的特性和波动规律。
其次,我们可以根据每个正弦波的振幅来合成原始的方波信号。
这种合成是通过将不同频率的正弦波按照其振幅进行叠加而实现的。
通过合成,我们可以得到与原始方波信号非常相似的近似信号。
这种信号合成的方法在通信、音频处理和图像处理等领域中非常实用。
在实际应用中,傅里叶变换和方波信号的分解是非常有指导意义的。
首先,当我们需要分析一个信号的频率特性时,可以通过傅里叶变换将其分解成不同频率的正弦波,从而获得有关信号频率特性的重要信息。
其次,当我们需要合成一个复杂的周期性信号时,可以根据傅里叶变换的结果,通过合成不同频率和振幅的正弦波来重建原始信号。
这种技术在信号处理、音频合成和图像合成等领域中得到了广泛应用。
综上所述,傅里叶变换是一个非常有用的工具,可以将一个信号拆解成不同频率的正弦波。
方波信号作为一种特殊的周期性信号,可以通过傅里叶变换来进行分解和合成。
通过这种分解和合成的方法,我们可以了解信号的频率特性,并且可以进行信号的重建和合成。
