方波信号f展开为傅里叶级数
- 格式:ppt
- 大小:1.42 MB
- 文档页数:83
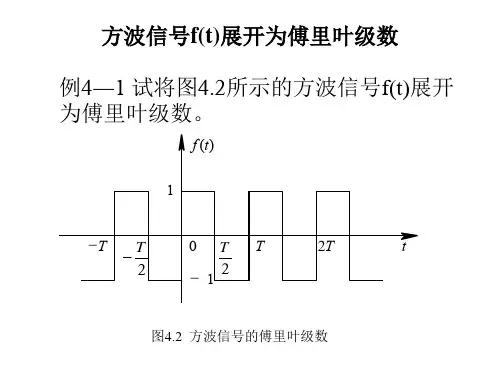


常见波形的傅里叶级数展开一、正弦波的傅里叶级数展开正弦波是一种最简单的周期性波形,可以通过傅里叶级数展开来表示。
傅里叶级数展开是将一个周期性函数表示为一组正弦函数的和的形式。
二、方波的傅里叶级数展开方波是一种周期为T的波形,它在一个周期内由两个不同幅值的水平线段组成。
方波可以通过傅里叶级数展开来表示,展开系数中包含各个谐波分量的幅值和相位。
三、三角波的傅里叶级数展开三角波是一种周期为T的波形,它在一个周期内由连续的线性上升和下降线段组成。
三角波可以通过傅里叶级数展开来表示,展开系数中包含各个谐波分量的幅值和相位。
四、锯齿波的傅里叶级数展开锯齿波是一种周期为T的波形,它在一个周期内由连续的线性上升和突然下降的线段组成。
锯齿波可以通过傅里叶级数展开来表示,展开系数中包含各个谐波分量的幅值和相位。
五、矩形波的傅里叶级数展开矩形波是一种周期为T的波形,它在一个周期内由连续的水平线段组成。
矩形波可以通过傅里叶级数展开来表示,展开系数中包含各个谐波分量的幅值和相位。
六、脉冲波的傅里叶级数展开脉冲波是一种非周期性的波形,它在一个有限时间内只有一个脉冲信号。
脉冲波可以通过傅里叶级数展开来表示,展开系数中包含各个谐波分量的幅值和相位。
七、高斯波包的傅里叶级数展开高斯波包是一种非周期性的波形,它的振幅随时间按高斯分布变化。
高斯波包可以通过傅里叶级数展开来表示,展开系数中包含各个谐波分量的幅值和相位。
八、噪声信号的傅里叶级数展开噪声信号是一种随机的信号,它包含了各种频率的谐波分量。
噪声信号可以通过傅里叶级数展开来表示,展开系数中包含各个谐波分量的幅值和相位。
以上是常见波形的傅里叶级数展开的简要介绍。
傅里叶级数展开是一种将周期性信号表示为谐波分量的和的方法,可以用来分析和合成各种复杂的波形。
通过傅里叶级数展开,我们可以更好地理解和描述各种波形的性质和特征。
傅里叶级数展开在信号处理、通信系统、音乐合成等领域具有广泛的应用。
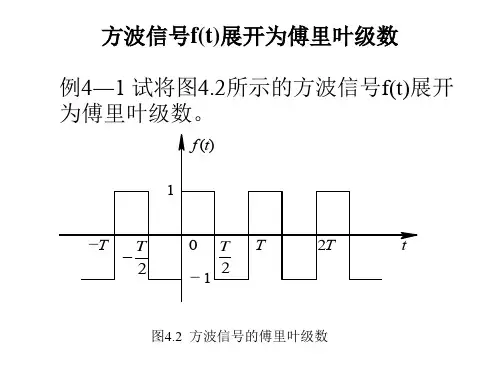





方波信号,作为一种常见的非正弦周期信号,在电子工程、信号处理以及控制系统中都有着广泛的应用。
方波信号具有简单的波形特征和易于生成的优势,因此在实际应用中经常用作测试信号或参考信号。
拉普拉斯变换,则是信号与系统分析中的一种重要数学工具,它能够将时域信号转换为复平面上的频域表示,从而方便我们分析和设计各种信号处理系统。
首先,我们来简要回顾一下拉普拉斯变换的基本概念。
拉普拉斯变换是一种积分变换,它通过引入复频率变量s,将时域函数f(t)转换为复平面上的函数F(s)。
这个转换过程可以表示为:F(s) = ∫[0, ∞) f(t) e^(-st) dt,其中s = σ + jω,σ和ω分别为复频率的实部和虚部。
拉普拉斯变换具有线性性、时移性、频移性、微分性和积分性等重要性质,这些性质使得它在信号与系统分析中发挥着重要作用。
然而,对于方波信号这样的非连续周期信号,其拉普拉斯变换并不是直接可得的。
因为方波信号在跳变点处存在不连续性,这导致拉普拉斯变换的积分过程在这些点上无法直接进行。
为了解决这个问题,我们可以采用一种间接的方法来计算方波信号的拉普拉斯变换。
具体来说,我们可以将方波信号分解为无穷多个正弦波的叠加,这是基于傅里叶级数展开的思想。
方波信号的傅里叶级数展开式为:f(t) = ∑[n=1, ∞] (4/(nπ)) sin((nπ/T)t),其中T为方波的周期。
然后,我们可以对每一个正弦波分量分别进行拉普拉斯变换,最后将变换结果相加得到方波信号的拉普拉斯变换。
对于正弦波分量sin((nπ/T)t),其拉普拉斯变换可以通过查找拉普拉斯变换表或直接计算得到。
正弦波的拉普拉斯变换结果为:F_n(s) = (nπ)/(T(s^2 + (nπ/T)^2))。
因此,方波信号的拉普拉斯变换可以表示为:F(s) = ∑[n=1, ∞] (4/(nπ)) F_n(s)。
需要注意的是,由于方波信号是非周期信号,其傅里叶级数展开是无穷级数,因此在实际计算中需要对级数进行截断处理。

mathematica 方波傅里叶级数方波是一种特殊的周期函数,其在一个周期内的取值只有两种可能:正值和负值。
在数学中,我们可以使用傅里叶级数来表示方波函数。
傅里叶级数是一种将周期函数表示为一系列正弦和余弦函数的方法。
方波函数可以用如下的傅里叶级数来表示:f(x) = (4/π) * (sin(πx) + (1/3)sin(3πx) + (1/5)sin(5πx) + ...)其中,x是自变量,f(x)是方波函数在x处的取值。
傅里叶级数的基本思想是将一个周期函数分解为多个正弦和余弦函数的和。
这些正弦和余弦函数称为频谱成分,它们的频率是周期函数的频率的整数倍。
在方波函数的傅里叶级数中,每个正弦函数的频率都是奇数倍的π。
傅里叶级数的系数可以通过积分来计算。
对于方波函数来说,每个正弦函数的系数都可以通过以下公式计算:An = (2/π) * ∫[0,1] f(x) * sin(nπx) dx其中,An是第n个正弦函数的系数,f(x)是方波函数在x处的取值。
利用这个公式,我们可以计算出方波函数的傅里叶级数的系数。
然后,将这些系数与对应的正弦函数相乘,并将它们相加,就可以得到方波函数的近似值。
通过调整傅里叶级数的阶数,我们可以控制近似的精度。
当阶数越高时,近似的精度越高,但计算量也会增加。
通常情况下,我们可以通过增加阶数来提高近似的精度,直到满足我们的要求为止。
傅里叶级数在信号处理、图像处理等领域有着广泛的应用。
通过将信号或图像分解为多个频谱成分,我们可以对其进行分析和处理。
傅里叶级数的理论基础也可以帮助我们理解信号和图像的特性,从而更好地应用于实际问题中。
总结一下,方波函数可以通过傅里叶级数来表示。
傅里叶级数将方波函数分解为多个正弦和余弦函数的和,通过调整阶数可以控制近似的精度。
傅里叶级数在信号处理、图像处理等领域有着广泛的应用,可以帮助我们理解和处理各种周期函数。

matlab方波信号傅里叶展开本文将介绍如何用MATLAB对方波信号进行傅里叶展开,并求出展开系数。
首先,我们需要了解什么是傅里叶展开和方波信号。
傅里叶展开是一种将周期函数表示为正弦和余弦函数的级数的方法。
而方波信号是一种由0和1交替组成的周期信号。
对于一个周期为T的方波信号,其数学表示为:f(t) = 1, 0 ≤ t < T/2f(t) = -1, T/2 ≤ t < Tf(t + T) = f(t)我们可以将这个信号用MATLAB画出来,代码如下:T = 2*pi; % 周期t = linspace(0, 4*T, 1000); % 时间范围f = sign(sin(t)); % 方波函数plot(t, f);接下来,我们将使用MATLAB的fft函数计算傅里叶变换,并用ifft函数计算傅里叶逆变换。
代码如下:N = length(f); % 信号长度F = fft(f)/N; % 傅里叶变换F(N/2+1:end) = []; % 取一半F(1) = F(1)/2; % 调整直流分量F = [F conj(fliplr(F))]; % 取共轭对称f_recon = ifft(F)*N; % 傅里叶逆变换f_recon(N/2+1:end) = []; % 取一半t_recon = linspace(0, T, N/2); % 时间范围plot(t, f);hold on;plot(t_recon, real(f_recon), 'r--');legend('原始信号', '重建信号');这段代码首先计算了傅里叶变换,并将其截取了一半,然后将其复制并取共轭对称,得到完整的傅里叶系数。
接着,使用ifft函数计算傅里叶逆变换,得到重建信号。
最后,我们可以将原始信号和重建信号画在同一张图上,比较它们的差异。
最后,我们可以用MATLAB的coeffs函数求出傅里叶展开的系数,代码如下:a0 = coeffs(f_recon(1), 'All');an = coeffs(f_recon*cos(n*t_recon), 'All');bn = coeffs(f_recon*sin(n*t_recon), 'All');其中,a0表示直流分量,an和bn分别表示余弦和正弦项的系数。