方波信号f(t)展开为傅里叶级数
- 格式:ppt
- 大小:1.46 MB
- 文档页数:83


几种常见函数的傅里叶变换及推导傅里叶变换是数学中一种非常重要的变换方法,它可以将一个函数在时域(或空域)中的表达转换为频域中的表达。
在信号处理、图像处理、通信等领域中被广泛应用。
本文将介绍几种常见函数的傅里叶变换及推导过程。
1. 方波函数的傅里叶变换方波函数是一种周期函数,它在每个周期内以不同的幅度交替出现。
方波函数的傅里叶变换可以通过将方波函数表示为一系列正弦函数的和来推导得到。
假设方波函数为f(t),其周期为T,傅里叶变换为F(ω)。
根据傅里叶级数展开的性质,方波函数可以表示为:f(t) = (1/2) + (2/π)sin(ωt) + (2/π)sin(2ωt) + (2/π)sin(3ωt) + ...其中,ω = 2π/T是方波函数的角频率。
根据傅里叶变换的定义,可以得到方波函数的傅里叶变换为:F(ω) = (1/2)δ(ω) + (1/2π)[δ(ω-ω0) - δ(ω+ω0)] + (1/2π)[δ(ω-2ω0) - δ(ω+2ω0)] + (1/2π)[δ(ω-3ω0) - δ(ω+3ω0)] + ...其中,δ(ω)是狄拉克函数,表示单位冲激函数。
傅里叶变换的结果是一系列的冲激函数,每个冲激函数对应一个正弦函数的频谱分量。
2. 高斯函数的傅里叶变换高斯函数是一种常用的连续函数,其在数学和物理学中有广泛的应用。
高斯函数的傅里叶变换可以通过将高斯函数表示为指数函数的平方和来推导得到。
假设高斯函数为f(t),傅里叶变换为F(ω)。
根据高斯函数的定义,可以得到:f(t) = e^(-αt^2)其中,α是常数。
根据傅里叶变换的定义,可以得到高斯函数的傅里叶变换为:F(ω) = √(π/α)e^(-ω^2/(4α))高斯函数的傅里叶变换仍然是一个高斯函数,只是幅度和频率发生了变化。
3. 矩形函数的傅里叶变换矩形函数是一种常见的函数,它在一个有限区间内的值为常数,而在其他区间内的值为零。
矩形函数的傅里叶变换可以通过将矩形函数表示为两个单位阶跃函数的差来推导得到。

傅里叶级数复指数展开公式傅里叶级数复指数展开公式是一种将任意周期函数展开为一系列正弦和余弦函数的方法。
它被广泛应用于信号处理、电子工程和物理学等领域。
在这篇文章中,我们将详细介绍傅里叶级数复指数展开公式,包括其基本原理、数学推导和应用示例。
首先,我们需要了解什么是傅里叶级数。
傅里叶级数是一种将任意周期函数表示为正弦和余弦波的和的方法。
考虑一个周期为T的函数f(t),它可以表示为如下形式的级数:f(t) = a0 + a1*cos(ωt) + a2*cos(2ωt) + a3*cos(3ωt) + ...其中,ω是频率,a0、a1、a2等是系数。
这个级数称为傅里叶级数展开。
现在,我们介绍傅里叶级数复指数展开公式。
傅里叶级数复指数展开公式将傅里叶级数中的余弦函数用复指数函数表示。
它的形式如下:f(t) = ∑(c_n*exp(inωt))其中,c_n是系数,n是一个整数,ω是角频率。
这个公式的好处是简化了计算,因为复指数函数具有较简单的性质。
为了推导傅里叶级数复指数展开公式,我们需要介绍欧拉公式。
欧拉公式是一个重要的数学公式,它将复指数函数表示为正弦和余弦函数的和:exp(iθ) = cos(θ) + i*sin(θ)将欧拉公式应用于傅里叶级数中的复指数项,可以得到:f(t) = ∑(c_n*cos(nωt) + i*c_n*sin(nωt))再将正弦函数用e^ix和e^-ix的形式表示,可以得到:f(t) = ∑(c_n/2*(e^(inωt) + e^(-inωt))) +∑(i*c_n/2*(e^(inωt) - e^(-inωt)))将上述两个级数合并,可以得到傅里叶级数复指数展开公式。
在展开公式中,每一项都是一个复指数函数的和,其中包含傅里叶级数的系数c_n和相应的频率nω。
傅里叶级数复指数展开公式具有广泛的应用。
例如,在信号处理中,它可以用于将信号分解为不同频率的正弦和余弦波的和,以便分析和处理。

傅里叶计算方波频率傅里叶分析是一种将一个信号进行频谱分解的数学方法。
它通过将信号分解为一系列正弦和余弦函数的和来描述其频谱内容。
方波信号是一种周期性信号,由一系列矩形脉冲组成,因此可以通过傅里叶分析来计算其频率。
要计算方波信号的频率,首先需要了解方波信号的数学定义。
方波信号可以定义为一个周期函数,其周期为T,占空比为d(d为0到1之间的值),即方波的脉冲宽度为dT。
方波信号可以用以下公式表示:f(t) = A * sign(sin(2πt/T))其中,sign是符号函数,其取值为1或-1,取决于sin(2πt/T)的正负号。
A是方波信号的幅值,t是时间。
接下来,我们需要将方波信号展开为一系列正弦和余弦函数的和,以便进行傅里叶变换。
根据傅里叶级数的定义,我们知道方波信号可以展开为如下形式的级数:f(t) = (4A/π) * [sin(2πt/T) + (1/3) * sin(6πt/T) + (1/5) * sin(10πt/T) + ...]这个级数包含了基频sin(2πt/T),以及一系列的谐波,其频率是基频的整数倍。
因此,我们可以通过计算这些谐波频率的整数倍来得到方波信号的频率。
首先,我们计算基频的频率。
基频对应于sin(2πt/T)的频率,即2π/T。
我们可以通过基频的周期来计算频率,即f = 1/周期。
对于方波信号,其周期为T,所以基频的频率为f0 = 1/T。
接下来,我们计算谐波的频率。
谐波对应于sin(nωt),其中n为整数,ω为基频的角频率,即2πf0。
我们可以通过将基频频率乘以谐波的整数倍来得到谐波的频率,即fn = n*f0。
例如,如果方波信号的周期为T=1秒,即频率为f0=1/T=1Hz。
那么基频的频率为f0=1Hz。
而第一个谐波的频率为f1=2f0=2Hz,第二个谐波的频率为f2=3f0=3Hz,以此类推。
通过计算基频和谐波的频率,我们可以得到方波信号的频率。
方波信号的频率是基频和所有谐波频率的集合。

方波信号合成与分解在信号处理领域中,方波信号是一种非常常见的信号类型。
它的特点是在一个周期内,信号的幅值会在两个固定的值之间来回变化。
方波信号的合成和分解是信号处理中的基本操作之一,本文将对这两个操作进行详细介绍。
一、方波信号的合成方波信号的合成是指将多个不同频率的正弦波信号叠加在一起,得到一个具有方波形状的信号。
这个过程可以用傅里叶级数展开来描述。
傅里叶级数是一种将周期信号分解成一系列正弦波的方法,它可以将一个周期为T的信号f(t)表示为以下形式的级数:f(t) = a0 + Σ(an*cos(nωt) + bn*sin(nωt))其中,a0是信号的直流分量,an和bn是信号的交流分量,ω是角频率,n是正整数。
对于方波信号,它的傅里叶级数可以表示为:f(t) = (4/π) * Σ(sin((2n-1)ωt)/(2n-1))其中,ω是角频率,n是正整数。
这个式子的意思是,将一系列正弦波信号按照一定的权重相加,就可以得到一个方波信号。
这个权重是由sin((2n-1)ωt)/(2n-1)这个函数决定的,它的图像如下所示:图1:sin((2n-1)ωt)/(2n-1)的图像可以看到,当n越大时,这个函数的周期越短,振幅越小。
因此,只需要取前几项的和,就可以得到一个近似的方波信号。
二、方波信号的分解方波信号的分解是指将一个方波信号分解成多个不同频率的正弦波信号的和。
这个过程可以用傅里叶变换来描述。
傅里叶变换是一种将时域信号转换成频域信号的方法,它可以将一个信号f(t)表示为以下形式的积分:F(ω) = ∫f(t)*e^(-jωt)dt其中,F(ω)是信号在频域上的表示,e^(-jωt)是复指数函数,j是虚数单位。
对于方波信号,它的傅里叶变换可以表示为:F(ω) = (2/π) * Σ(1/n * sin(nω/2))这个式子的意思是,将一个方波信号在频域上表示为一系列正弦波信号的和,其中每个正弦波信号的频率是nω/2,振幅是1/n。

方波信号的傅里叶级数展开方波信号是一种特殊的周期信号,在每个周期内信号值交替地取正弦波的最大值和最小值。
它可以用傅里叶级数展开来表示,下面我将详细介绍关于方波信号的傅里叶级数展开的相关内容。
傅里叶级数是一种将一个周期性函数分解为一系列正弦和余弦函数的无穷级数的表示方法。
对于一个周期为T的函数f(t),其傅里叶级数表示为:f(t) = a0/2 + Σ(an*cos(nωt) + bn*sin(nωt))其中,a0/2表示直流分量,an和bn分别表示正弦和余弦分量的系数,ω为角频率,等于2π/T。
对于方波信号,其周期为T,即一个周期内正弦波的最大值和最小值的持续时间。
方波信号可以表示为一个由无限多个正弦波组成的傅里叶级数。
在方波信号的傅里叶级数展开中,直流分量a0/2表示方波的平均值,等于正弦波最大值和最小值的平均值。
对于幅值为A,周期为T的方波信号,其直流分量a0/2等于A/2。
正弦和余弦分量的系数an和bn可以通过积分计算得到。
由于方波信号在一个周期内的正弦和余弦分量只有在0到T/2的时间段内有贡献,所以对an和bn的计算可以将积分区间限制在0到T/2。
根据傅里叶级数的定义,an和bn的计算公式为:an = (2/T) * ∫[0,T/2] (f(t)*cos(nωt) dt)bn = (2/T) * ∫[0,T/2] (f(t)*sin(nωt) dt)其中,f(t)为方波信号。
对于方波信号,可以将其正弦和余弦分量表示为:an = (2/T) * ∫[0,T/2] (A*cos(nωt) dt)= (2/T) * (A/nω) * [sin(nωt)] from 0 to T/2= (2/T) * (A/nω) * sin(nωT/2)bn = (2/T) * ∫[0,T/2] (A*sin(nωt) dt)= (2/T) * (-A/nω) * [cos(nωt)] from 0 to T/2= (2/T) * (-A/nω) * [cos(nωT/2) - 1]根据傅里叶级数展开的定义,方波信号可以表示为:f(t) = A/2 + Σ[(2A/(nπ)) * sin(nωt)] from n = 1 to ∞其中,A为方波信号的幅值,T为方波信号的周期。

方波信号的傅里叶级数
方波信号是一种典型的周期信号,其波形为一段时间内等幅的正弦波,然后突然反向等幅的负正弦波,如此往复。
方波信号的傅里叶级数是
将其分解为一系列正弦波的和,是信号处理中重要的基础理论之一。
傅里叶级数的基本思想是将一个周期信号分解为一系列正弦波的和,
这些正弦波的频率是原始信号频率的整数倍。
对于方波信号,其周期
为T,可以表示为:
f(t) = A/2 + Σ(A/nπ)sin(nπt/T)
其中A为方波信号的幅值,n为正整数,表示正弦波的次数。
这个式
子可以理解为,方波信号可以分解为一系列正弦波的和,每个正弦波
的振幅和频率都不同,但都是原始信号频率的整数倍。
傅里叶级数的计算可以通过复杂的积分公式来完成,但是在实际应用中,通常使用离散傅里叶变换(DFT)来计算。
DFT是一种将时域信
号转换为频域信号的算法,可以将一个N点的离散信号转换为N个频率分量的复数值。
对于方波信号,可以通过DFT算法计算出其傅里叶
级数的系数,从而得到每个正弦波的振幅和频率。
傅里叶级数的应用非常广泛,例如在音频和图像处理中,可以使用傅
里叶级数将信号转换为频域信号,从而实现滤波、降噪、压缩等处理。
此外,在通信系统中,傅里叶级数也被广泛应用于信号调制和解调中。
总之,方波信号的傅里叶级数是将其分解为一系列正弦波的和,是信
号处理中重要的基础理论之一。
通过傅里叶级数的计算,可以得到每
个正弦波的振幅和频率,从而实现各种信号处理和调制解调等应用。
占空比方波傅里叶级数占空比是指周期信号中,高电平所占的时间与一个周期时间的比值。
在电子电路中,占空比是一个非常重要的参数,它可以用来控制电路的输出信号的特性。
在数字电路中,占空比可以用来控制脉冲的宽度,从而实现数字信号的编码和解码。
在模拟电路中,占空比可以用来控制信号的幅度和频率,从而实现信号的调制和解调。
方波是一种周期信号,它的周期是固定的,而且在一个周期内,信号的幅度会从高电平快速切换到低电平,然后再从低电平快速切换到高电平。
方波信号的占空比可以通过控制高电平和低电平的时间比例来实现。
当高电平时间占整个周期的一半时,方波信号的占空比为50%。
当高电平时间占整个周期的三分之一时,方波信号的占空比为33.3%。
当高电平时间占整个周期的四分之一时,方波信号的占空比为25%。
傅里叶级数是一种将周期信号分解成一系列正弦波的方法。
它可以将任何周期信号表示为一组正弦波的叠加。
傅里叶级数的基本思想是,任何周期信号都可以看作是一系列正弦波的叠加。
这些正弦波的频率是原始信号的基频率的整数倍。
傅里叶级数可以用来分析周期信号的频谱特性,从而帮助我们理解信号的性质和行为。
在傅里叶级数中,每个正弦波的振幅和相位都可以通过计算原始信号的积分来确定。
这个积分的计算可以使用傅里叶级数的公式来完成。
傅里叶级数的公式是一个无限级数,它包含了所有可能的正弦波。
在实际应用中,我们通常只需要计算前几个正弦波的振幅和相位即可。
对于方波信号,它可以表示为一组奇次谐波的叠加。
奇次谐波是指频率为基频的奇数倍的正弦波。
例如,对于一个基频为f的方波信号,它的第一个奇次谐波的频率为3f,第二个奇次谐波的频率为5f,以此类推。
因此,方波信号的傅里叶级数可以表示为以下形式:f(t) = (4/pi) * sin(wt) + (4/3pi) * sin(3wt) + (4/5pi) * sin(5wt) + ...其中,w是基频的角频率,t是时间,pi是圆周率。
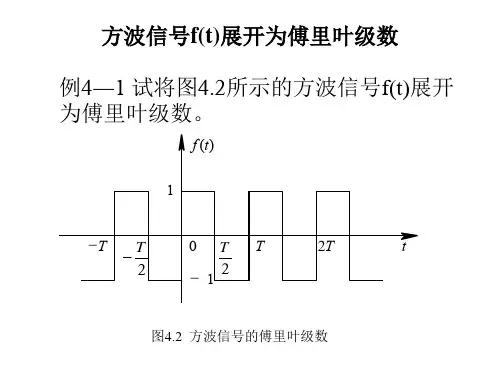
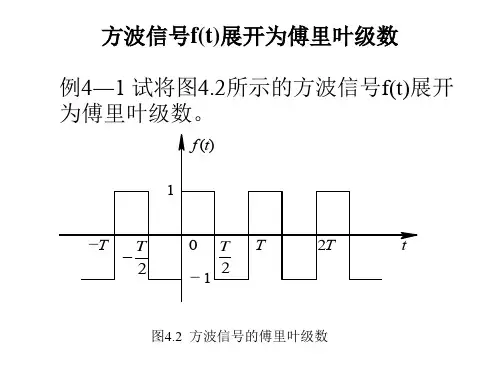
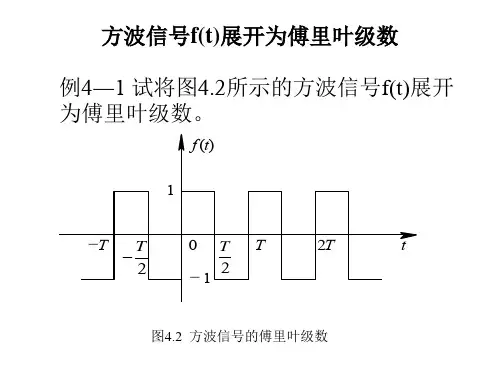
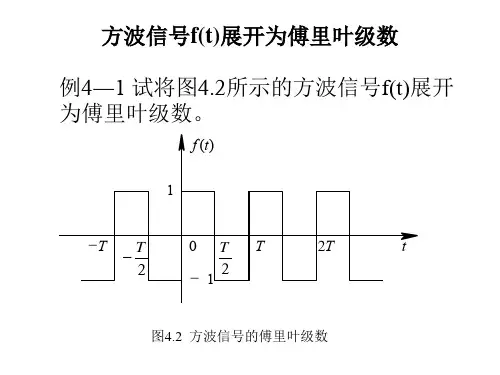
【例4.2-1】将下图所示方波信号展开为傅里叶级数。
…… 0 ……
2T - 2T t
解:按题意方波信号在一个周期内的解析式为 分别求得傅里叶系数: cos 22cos 22200020⎰⎪⎭
⎫ ⎝⎛+⎰⎪⎭⎫ ⎝⎛-=-T T n tdt n E T tdt n E T a ωω 即: ⎪⎩⎪⎨⎧=为偶数为奇数n n n E b n 02π
故得信号的傅里叶级数展开式为
它只含有一、三、五、……等奇次谐波分量。
【例4.2-2】将下图所示信号展开为傅里叶级数。
2
…… 0 ……
0T - 20T - 20T 0T t
-2
解:
首先将图示信号分解为奇、偶函数,如下图(a)、(b)所示。
…… 1 ……
0T - 20T - 20T 0T t
-1
(a)
…… 1 ……
0T - 20T - 0 20T 0T t
-1
(b)
从图(a)可见为一个半波反对称偶函数。
在这种情况下,其傅里级数展开式中将只含有余弦项,且只含奇次谐波分量而不含偶次谐波分量,即有:从图(b) 可见为一个半波反对称奇函数。
在这种情况下,其傅里级数展开式中将只含有正弦项,且只含奇次谐波分量而不含偶次谐波分量,即有:
田七,三七的区别YNQInyMDOe0W。
方波信号的傅里叶级数展开引言方波信号是一种特殊的周期信号,具有周期性、对称性和离散性的特点。
为了研究方波信号的频谱特性,我们需要进行傅里叶级数展开。
傅里叶级数的定义傅里叶级数是一种将周期信号表示为一系列正弦波的和的方法。
它的定义如下:f (t )=a 02+∑(a n cos (nω0t )+b n sin (nω0t ))∞n=1 其中,f (t )是周期为T 的周期信号,ω0=2πT 是基本角频率,a 0、a n 、b n 是系数。
方波信号的定义方波信号是一种以一定周期T 切割的周期信号,其定义如下:f (t )={1,0<t <T/2−1,T/2<t <T这个定义意味着方波信号在一个周期内,前一半时间的幅值为1,后一半时间的幅值为-1。
方波信号的傅里叶级数展开现在我们来对方波信号进行傅里叶级数展开。
首先计算a 0,根据公式:a 0=2T ∫f T(t )dt 由于方波信号在一个周期内等于1和-1,可以得到:a 0=2T ∫f T 0(t )dt =2T (∫1T/20dt +∫−T T/21dt)=0 可见,方波信号的直流分量为0。
接下来我们计算a n和b n。
根据公式:a n=2T∫fT(t)cos(nω0t)dtb n=2T∫fT(t)sin(nω0t)dt根据方波信号的定义,在一个周期内,只有在0<t<T/2范围内,f(t)的值为1,因此上述积分变为:a n=2T∫cosT/2(nω0t)dtb n=2T∫sinT/2(nω0t)dt对上述积分进行计算,可以得到:a n=2T⋅sin(nω0t)nω0|0T/2=2nπsin(nπ/2)b n=2T⋅−cos(nω0t)nω0|0T/2=2nπ(−1)n+1由上式可以看出,当n为奇数时,b n为4nπ;当n为偶数时,b n为0。
因此,方波信号的傅里叶级数展开为:f(t)=∑4 (2n−1)π∞n=1sin((2n−1)ω0t)方波信号的频谱特性方波信号的傅里叶级数展开给出了其频谱特性。