大冈中学2010届高三数学小题训练16(2010

2010数学高考模拟试题（文理合卷）【命题报告】本套试卷在命题前，详细地剖析了最新的2010年《考试大纲》，对高考的热点、难点和重点进行了全面的研究。

命题时，注重对基础知识的全面考查，同时又强调考查学生的思维能力。

在试题的设计上，进行了一些创新尝试。

比如第8、12、16 （理）题是对能力要求较高的题，第11题是导数、反函数与不等式的综合小问题，题型比较新。

命题时还在知识点的交汇点处设计试题，强调知识的整合，比如第2 题是向量与数列，第9题是向量与三角函数，第15题球内接几何体，第22题是向量与解几的结合，第12题是函数与数列的结合，第14题是函数性质与双曲线的结合，第16题是数列与概率的结合。

总之本套试卷很好地代表了高考的命题趋势和方向。

考生注意：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟。

2．答卷前将密封线内的项目填写清楚。

第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题；每小题5分，共60分，在每小题给出的四个选项中，只有一项是最符合题目要求的。

1、（理）已知实数b 是关于x 的方程2(6)90x i x ai -+++=()a R ∈的解，则a b +的值为 ( )A. 0B. 3C. 6D. 9（文）不等式组(3)()004x y x y x -++≥⎧⎨≤≤⎩表示的平面区域是 ( )A. 矩形B. 三角形C. 直角梯形D. 等腰梯形 2、（理）已知等差数列}{n a 的前n 项和为n S ，若1200920a OA a OB OC ++=，且A 、B 、C 三点共线（该直线不过原点），则2009S = （ ） A. 2009 B. 2010 C. -2009 D. -2010 （文）设P 为ABC ∆内一点，且3145AP AB AC =+，则ABP ∆的面积与ABC ∆面积之比为 （ ）A.14 B. 34 C. 15 D. 453、若P 为双曲线221445x y -=的右支上一点，且P 到左焦点1F 与到右焦点2F 的距离之比为4:3，则P 点的横坐标x 等于 （ ）A. 2B. 4C. 4.5D. 54、已知1()10x f x x <≤=-≤<⎪⎩，且0||1,0||1,0m n mn <<<<<，则使不等式()()f m f n >-成立的m 和n 还应满足的条件为（ ）A m>nB m <nC m+n>0D m+n<0 5、曲线sin(2)(0,0,0)y M x N M N ωφω=++>>>在区间],0[ωπ上截直线y=4，与y=－2所得的弦长相等且不为0，则下列描述中正确的是（ ）A ．3,1>=M NB ．3,1≤=M NC ．23,2>=M N D ．23,2≤=M N6、函数322()2103f x x x ax =-++在区间[1,4]-上有反函数，则a 的X 围为是 ( )A. (,)-∞+∞B.[)2,+∞C.(16,2)-D. (][),162,-∞-⋃+∞7、（理）用1到9这9 个数字组成没有重复数字的三位数，则这个三位数是3的倍数的概率为（ ）A.128 B.928 C. 514 D.12（文）用1到5这5 个数字组成没有重复数字的三位数，则这个三位数是的倍数的概率为（ ） A. 110 B.310 C. 25 D.458、ABC ∆的BC 边在平面α内，A 在α上的射影为A '，若BAC BA C '∠>∠，则ABC ∆一定为 （ ）A 、 锐角三角形B 、直角三角形C 、 钝角三角形D 、 以上都不是9、已知A ，B ，C 三点的坐标分别是(3,0)A ，(0,3)B ，(cos ,sin )C αα，3,22ππα⎛⎫∈ ⎪⎝⎭，若1AC BC ⋅=-，则21tan 2sin sin 2ααα++的值为（ ） A, 59-B, 95-C, 2 D, 3 10、函数13x y a+=-(0,1)a a >≠的图象恒过定点A ，若点A 在直线10mx ny ++=上，其中0mn >，则21m n+的最小值为 （ ） A. 6 B. 8 C. 10 D. 1211、（理） 已知函数2||(0)y ax b x c a =++≠在其定义域内有四个单调区间，且,,a b c ∈{2,1,0,1,--2,3,4}，在这些函数中，设随机变量ξ=“||a b -的取值 ”，则ξ的数学期望E ξ为 ( )A. 4B.295 C. 25 D. 89（文）若21091001910(1)(1)(1)x x a a x a x a x +=+++++++……，则9a 等于（ ）A. 9B. 10C. -9D. -10 12、（理）对数列{}n x ，满足143x =，1331n n n x x x +=+；对函数()f x 在(2,2)-上有意义，122f ⎛⎫-= ⎪⎝⎭，且满足,,(2,2)x y z ∈-时，有()()()1x y z f x f y f z f xyz ⎛⎫++++= ⎪+⎝⎭成立，则 ()n f x 的表示式为 （ ）A. 2n -B. 3nC. 23n-⨯ D.23n ⨯（文）对数列{}n x ，满足145x =，1221n n n x x x +=+；对函数()f x 在(2,2)-上有意义，122f ⎛⎫=- ⎪⎝⎭，且满足,(2,2)x y ∈-时，有()()1x y f x f y f xy ⎛⎫++= ⎪+⎝⎭成立，则数列 {}()n f x 是 （ ）A. 以4-为首项以2为公差的等差数列B. 以4-为首项以2为公比的等比数列C. 既是等差数列又是等比数列D. 既不是等差数列又不是等比数列第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题5分，共20分．把答案填在题中横线上．13、（理）点P 在焦点为12(0,1),(0,1)F F -，一条准线为4y =的椭圆上，且1215||||4PF PF ⋅=，12tan F PF ∠____________。

2010届高三数学上册期中考试试卷高三 文科数学（时间：120分钟，满分：150分）第Ⅰ卷（选择题 ： 共60分）一、选择题：本大题共１２题，每小题５分，共６０分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设集合{}{}22|21,|25M y y x x N x y x x ==++==-+ ，则 等于 （ ）A ．∅B ．(){}4,1C ．[)+∞,4D ．[)+∞,02．下列说法正确的是 （ ） A. 函数在闭区间上的极大值一定比极小值大; B. 函数在闭区间上的最大值一定是极大值; C. 对于12)(23+++=x px x x f ,若6||<p ,则)(x f 无极值;D.函数)(x f 在区间),(b a 上一定存在最值.3．在等差数列1077,21,5,,}{S S a S n a n n 那么若项和为前中==等于 （ ）A ．55B ．40C ．35D ．704．已知等差数列{}n a 中，4,84111073=-=-+a a a a a ，记...=+++n 12n S a a a ，则S 13= （ ）A ．78B ．152C ．156D ．1685．若正项数列}{n a 满足043,221211=--=++n n n n a a a a a ，则}{n a 的通项n a = ( ) A.122-=n n a B.2n n a = C.212n n a += D.232n n a -=6．函数)01(312<≤-=-x y x的反函数是 （ ）A ．)31(log 13≥+=x x y B ．)31(log 13≥+-=x x yC ．)131(log 13≤<+=x x yD ．)131(log 13≤<+-=x x y7．已知条件p ：2|1|>+x ，条件q ：a x >，且p ⌝是q ⌝的充分不必要条件，则a 的取值范围可以是 （ ）A ．1≥a ；B ．1≤a ；C ．1-≥a ；D ．3-≤a ；8．若函数()()1(01)x x f x k a a aa -=-->≠且在R 上既是奇函数，又是减函数，则()()log x k a g x +=的图象是 （ ）9．若)(x f是R 上的减函数，且)(x f 的图象经过点(0,4)A 和点(3,2)B -，则当不等式3|1)(|<-+t x f 的解集为（－1，2）时，t 的值为（ ）A ． 0B ．－1C ．1D ．210．函数223)(a bx ax x x f +--=在1=x 处有极值10, 则点),(b a 为 （ ） A.)3,3(- B.)11,4(- C. )3,3(-或)11,4(- D.不存在 11．若函数2(2)()m x f x x m-=+的图象如图所示，则m 的范围为( A ．（－∞，－1） B ．（－1，2）C ．（1，2）D ．（0，2）12．已知函数)(x f 是定义在实数集R 上的不恒为零的偶函数，且对任意实数x 都有 )()1()1(x f x x xf +=+，则)25(f 的值是( )A 1A. 0B.21 C. 1 D. 25 第Ⅱ卷（非选择题 共90分）二、填空题：（本大题共４小题，每小题5分，共20分.） 13．若cos(2)πα-=且(,0),sin()2παπα∈--=则_________ 14．.已知()1323+-+=x x ax x f 在R 上是减函数，求a 的取值范围。

福州三中2010—2011学年度高三上学期期中考试数学（理）试题本试卷分第I卷（选择题）和第II卷（非选择题）两部分共150分，考试时间120分钟。

注意事项：1•答第I卷前，考生务必将自己的姓名、考生号码（31103XXXX XXXX为班级+ 座号）、考试科目用铅笔涂写在答题卡上。

2•每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上。

3•考试结束，监考人将答题卡收回。

第I卷（选择题共50分）选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的•1(211 .设集合A= Q X -一£ X £2、B=(X X <1 ,I 2 JA . ：x1< x<2；C .「XX:::2 /64cos71的2 .已sin ，值为2577A B.-25253 .等比数列a』中，4 =4 ,则a日6等于A.4B. 8A. x R,lg x =0B. x R,tanx =1则A U B=( )1 1B—<x G\I 2 JD.l x-1Exc2}( ) 44C— D. ——55( ) C.16D.32( ) C.Vx ER, X3A0D.時R,2X>04 .下列命题中的假命题.是：•_：,：•_ ，: = m,贝 U m _ ?&某种商品一年内每件出厂价在7千元的基础上，按月呈f(X )二"A >0>0|申|£上i 的模型波动(x 为月份)，已知3月份达到最高价 9千元, \ 2)份价格最低为5千元，根据以上条件可确定 f (X)的解析式为9•如图，圆o 的内接 五角星”与圆o 交与A (i =1,234,5,)点，记弧AA41在圆0中所对的圆心角为a/i =1,2,3,4,),弧愿A 所对.啲圆心角为a 5 ,则c o3as c oas t a 5) —s i 3a 2 s i 2a 4 =― 3 5 .已知 ot € (—，兀),sin ot =—，贝V tan ( G + )等于254 11A .B . 7C.——7 7B . 7 D .— 76. m 、n 表示直线，:-J ：-,表示平面，给出下列四个命题，其中真命题为(1) 匚 -m, n 二 x , n _ m,贝卜 l : (2) :-二 m,： 二 n,贝Un _ m (3) (4)m _ : , n 」i ,m _ n,贝U:--:A . (1 )、(2)B . ( 3)、(4)C. (2)、 (3)D . (2)、 (4)7.将函数y=3sin(x-v)的图象F 按向量(—,3)平移得到图象3F'若F 的一条对称轴是直线TtX ，则B 的一个可能取值是45 A. ■:12 5 B .12 11 C. 11D.-■:Asin(「) BA . nn*f (x) = 2sin( x )7 (1 乞 x 乞 12,x N )44JIJIB . C.f (x) =9sin( [X -[) (1 _ x _12,x N ) f(x)=2、-2s in — x 7(仁 x^12,x N )43171D . f(x)=2sin(;x — ;) 7(仁x ^12,x N )-20 A .B .C .D .10•已知函数y = f(x)和y =g(x)在[-2,2]的图象如下所示 y=f(x)四个命题：(1 )方程f[g(x)]=0有且仅有6个根；ee dLkx = -2 x12.已知向量 a = (3,1),b =(1,3),c =(k,2)，若(a_c)丄 b ，则实数 k =13.已知极坐标系的极点在直角坐标系的原点 O 处，极轴与x 轴的正半轴重合.直线l 的极2x = 2cos -坐标方程为「si n (八)二 ，圆C 的参数方程为(参数y =g(x)给出下列(2 )方程g[ f (x)] 二0有且仅有3个根；(3)方程f[ f (x)H 0有且仅有5个根； (4)方程g[g(x)] 二0有且仅有4个根•其中正确的命题个数A . 1B . 2第II 卷 (非选择题共100 分)填空题：本大题共 5小题，每小题4分，共20分，把答案填在答题卡的相应位置.11 .C.-2 04 2 ly = 2si n 日+2日乏b,2让))，则圆心C到直线l的距离等于_________________2 214. 过双曲线 冷-爲=1的左焦点F 且垂直于x 轴的直线与双曲线相交于 M , N 两点，且a b双曲线的右顶点 A 满足MA _ NA ，则双曲线的离心率等于 _________________ .15. 符号X 1表示不超过x 的最大整数，如口！二丨-3丄1.081 - -2 ，定义函数｛x ｝ = X - IXI .那么下列命题中正确的序号是 _____________ .①函数｛x ｝的定义域为R ,值域为0,1】. ② 方程 有无数多个解.③函数｛x ｝是周期函数. ④函数｛x ｝是增2函数.三、解答题：本大题共 6小题，共80分，解答应写出文字说明、证明过程或演算步骤.16. 本题（1 ）、（2）两个必答题，每小题 7分，满分14分.（1）（本小题满分7分）已知x,y, z 为正实数，且1 1，求x 4y 9z 的最小值及取得最小值时 x, y, z 的x y z值.（2）（本小题满分7分）已知矩阵A = "333 ，若矩阵A 属于特征值6的一个特征 ^cd d17.（本小题满分 13分）已知f （x ）二3sin2x ' 2 ■ 2cos 2 x . （1 ）求f （x ）的最小正周期与单调递减区间； （2 ）在 ABC 中，a 、b 、c 分别是角 A 、B 、C 的对边，若向量为玄="，属于特征值1的一个特征向量为d 丿a 2勺［求矩阵A . 1一2丿能使整个矩形广告面积最小.19.（本小题满分13分）盒内有大小相同的 9个球，其中2个红色球，3个白色球, 4个黑色球.规定取出1个红色球得1分，取出1个白色球得0分，取出1个黑色球得-1分•现f (A) =4, b =1, .'ABC 的面积为 ，求a 的值.218.（本小题满分13分）迎世博，要设计如图的一张矩形广告，该广告含有大小相等的左中2右三个矩形栏目， 这三栏的面积之和为 60000cm ，四周空白的宽度为10cm , 之间的中缝空白的宽度为 5cm ，怎样确定广告矩形栏目高与宽的尺寸（单位: 栏与栏cm ），（单位:出的3个球中白色球的个数，求的分布列和数学期望.从盒内一次性取3个球.(1)求取出的3个球得分之和恰为1分的概率；(2)设•为取2 220.(本小题满分13 分)设椭圆C：笃爲=1 (a,b 0)的左、右焦点分别为F I,F2 ,若Pa bT T 1是椭圆上的一点，PR十PF? =4，离心率e=—. (1)求椭圆C的方程；(2)若P是第25一象限内该椭圆上的一点，PF1PF2，求点P的坐标；(3)设过定点P(0,2)的直线4与椭圆交于不同的两点代B,且/ AOB为锐角(其中O为坐标原点)，求直线丨的斜率k的取值范围.1 2 121.(本小题满分14分)已知函数f(x)=lnx, g(x) ax bx. (1 )当a = b 时，求2 2函数h(x) = f (x)- g(x)的单调区间；(2)若b = 2且h(x) =f (x) £(x) 存在单调递减区间，求a的取值范围；(3)当a=0时，设函数f(x)的图象C与函数g x的图象C2 交于点P、Q,过线段PQ的中点R作x轴的垂线分别交G、C于点M、N，则是否存在点R,使G在点M处的切线与C2在点N处的切线平行？如果存在，请求出R的横坐标，如果不存在，请说明理由.【校本試卷】2010/11/04福建省福州三中2010届高三上学期半期考数学理科参考答案第I 卷（选择趣共50分）选tffi ： 10^8. B 4^8 5 ft.共50 ft.在毎小U 给出的POf 选敗中.只有一取是符合邕口要来的. 【解析】D 【解析】B 【解析】C 【解析】C 【解析】 【解析】 【解析】 【解析】 【解析】【解析】当11仅当x = 2y = 3z 时等号成立.此时x=6,y = 3,z = 2 所以当x = 6j ，= 3,z = 2时.x + 4y + 9z 取得最小值36…(2)解：(1)依题意得c +d = 6 所以l3c-2"-2解得17. 解:<1) f (x) .................................................................... sin2x+2 + 2co^ x =>|'3siri2x+cos2x+3=2sin(2x - —) + 3 ............................................................../. T == n ...... 4 分21. 2. 3. 4. 5. 6. 7. &9.10.A B A D D C二、填空套: |】・ 12. 【解析】 【解13. 【解析】 第II 卷（非选择题共100分）每爪前4价.共20什，把苔果瞋在告总的fflBER.本大8H5^8.l-ln2 0 722 214・15. 三、解§«：本大&共6"、总・ 16. (1) *?：由柯西不等式得“ 4y + 9z =[(以)2 + (2&)2 +(3血)2 ]. [(±)2 +(金)2 +(十)2 ]2(侬•厶+ 2“・厶+ 3血•車)2 =36Vx yjy \!z【解析】 【解析】②®共80仔.解答应写出文字说明.演茸步iL —• —< Aa } = 6q 彳幻=“2，即令j < 2x + 2kn + ^-(keZ)< x <^ + ?^(k€ Z)rr 7/. f(x)的单调区间为［k7t + —,k7r +kez ................................. 6 分6・ 3*⑵由/(,4) = 4得心) = 2sin(2卄兰) + 3 = 4 ・・・sin(2/+夕)=£ ...... 7分6 6 * 2乂•： A 为 的内角.\-<24 + -<— ：.2A^^ = — ：\A = - ..................................... 9 分666663'：S^ftc =^~、b = \ :. —/>csin A -:.c = 2 .............. 11 分2 2 2/. a 2 =62 +c 2 - 26c cos J = 4 + l-2x2xlx 丄=3/. a = V3 ................ 12 分 2200001&繇：设矩形栏目的髙为acm.宽为bcm.则a6 = 20000. .-.6 = ^^a广吿的高为a+20,宽为36 + 30(其中Q >0』>0) 广告的面积S = (fl + 20)(36 + 30)= 30(0 + 26) + 60600 = 30(a +毁也)+ 60600>30x 2」a x 毁型 + 60600 = 12000 + 60600 = 72600肖且仅当Q =型巴，即Q = 2(M)时，取等号，此时b = 100・故当广告的高为200am 宽为100cm 时.可使广告的面积最小.19.(I 〉解：记“取出1个红色球，2个白色球”为爭件“取出2个红色球.1个黑色球"为爭件B. 则取出3个球得分之和恰为1分为事件A+B. 则 P(/f + B) = P(£ + P(B) = ^~+^_ = ^ (2)解：歹可能的取值为0,1,23. 佗=0)=£|=丄， w CJ 21C 2C l 320•解：(I) —+ /=14 (2) •解：易知a=2上== J5所以片(一巧.0)迅(VLO). 05 则w > C ； 14 q 28 = 3) = g =丄.Cl 8410分 •绅数学期望#。

嘉定区2010学年高三年级第一次质量调研 数学试卷（理）参考答案与评分标准一．填空题（本大题满分56分）本大题共有14题，考生必须在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分． 1．答案：1．因i a a ai i )1(1)1)(1(-++=-+是实数，所以=a 1． 2．答案：]2,0[．由022≥-x x ，得022≤-x x ，所以]2,0[∈x ． 3．答案：1．112+=a a ，314+=a a ，由已知得4122a a a =，即)3()1(1121+=+a a a ，解得11=a ． 4．答案：257-．由532sin =⎪⎭⎫ ⎝⎛+θπ，得53cos =θ，所以2571cos 22cos 2-=-=θθ．5．答案：2-．解法一：函数x x f -=)(的反函数为21)(x x f =-（0≤x ），由4)(1=-x f 得42=x ，因为0<x ，故2-=x ．解法二：由4)(1=-x f ，得2)4(-==f x ．6．答案：105arccos． 因为AB ∥11B A ，故1BAC ∠就是异面直线1AC 与11B A 所成的角，连结1BC ，在1ABC 中，1=AB ，511==BC AC ，所以10552121cos 11===∠AC ABBAC ．7．答案：0．因)(x f 是定义在R 上的奇函数，所以0)0(=f ，在等式)()2(x f x f -=+中令2-=x ，得0)2(=-f ． 8．答案：2．9)21(x -展开式的第3项为288)2(2293=-=x C T ，解得23=x ，所以232132132lim 323232lim 111lim 22=-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+++∞→∞→∞→nn nn n n x x x ．9．答案：1．三阶行列式xa x 1214532+中元素3的余子式为xa x x f 21)(+=，由0)(<x f 得022<-+ax x ，由题意得a b -=+-1，所以1=+b a ．10．答案：16．1=a ，满足3≤a ，于是4211==+b ；2=a ，满足3≤a ，8212==+b ；3=a ，满足3≤a ，则16213==+b ；4=a ，不满足3≤a ，则输出b ，16=b ．11．答案：21．满足条件的选法可分为三类：A 组2人，B 、C 组各1人，有121325C C C 种选法；B 组2人，A 、C 组各1人，有122315C C C 种选法；C 组2人，A 、B 组各1人，有221315C C C 种选法．所以A 、B 、C 三组的学生都有的概率21210105410221315122315121325==++=C C C C C C C C C C P ． 12．答案：65π．由题意，612cos 2>θ且212sin 2>θ，⎩⎨⎧==+22cos 34ab b a θ，⎪⎪⎩⎪⎪⎨⎧=⋅-=+21112sin 211a b a b θ，所以θθ2sin 22cos 32-=，32tan -=θ，因)2,(2ππθ∈，故352πθ=，65πθ=．13．答案：①③④．由y x y f x f ⋅=⋅)()(，得y x a y a y a x a x⋅=⋅⋅-⋅⋅⋅-])(2[])(2[，化简得)()()()(2y a x a a y a x a ⋅⋅⋅=⋅⋅⋅⋅，当0 =a 时，等式成立；当0 ≠a 时，有12=a ，即1||=a，所以①、③、④都能使等式成立． 14．答案：4．11+<<t a t ，则t t a a <<-=112，t t a t a t a >+>-+=-+=1222123，t a t t a a <-+=-=1342，1452a a t a =-+=．所以}{n a 是以4为周期的周期数列．（第14题也可取满足条件的t 和1a 的特殊值求解）二．选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生必须在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分． 15．C ．16．A ．17．D ．16．B ．15．由5:4:3::=c b a 可得a ，b ，c 成等差数列；若a ，b ，c 成等差数列，则c a b +=2，由勾股定理，222c b a =+，得2222c c a a =⎪⎭⎫ ⎝⎛++，032522=-+c ac a ，解得53=c a ，令k a 3=（0>k ），则k c 5=，得k b 4=．所以5:4:3::=c b a ．16．①错．不在同一直线上的三点才能确定一个平面；②错．若圆锥的侧面展开图是一个圆面，则可得圆锥底面半径的长等于圆锥母线的长；③错．如果三棱锥的底面是等边三角形，一条侧棱垂直于底面且长度等于底面边长，则三个侧面都是等腰三角形；④错．若这两点是球的直径的两个端点，过这两点可作无数个大圆．17．作出函数xy 2=与2x y =，可发现两函数图像在第二象限有一个交点，在第一象限有两个交点（第一象限的两个交点是)4,2(和)16,4(）．18．若取1x 、2x 为区间]4,2[的两个`端点，则8)()(21=x f x f ．若8>C ，取21=x ，4)(1=x f ，对任意]4,2[2∈x ，16)(2≤x f ，于是8)(4)()(221≤=x f x f x f ；若8<C ，取41=x ，16)(1=x f ，对任意]4,2[2∈x ，4)(2≥x f ，于是8)(16)()(221≥=x f x f x f ．所以8=C ．三．解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤． 19．（本题满分12分） 解：设半圆的半径为r ，在△ABC 中，090=∠ACB ，030=∠ABC ，3=BC ， 连结OM ，则AB OM ⊥，……（2分） 设r OM =，则r OB 2=，…………（4分） 因为OB OC BC +=，所以r BC 3=，即33=r ．………………（6分）130tan 0=⋅=BC AC ．阴影部分绕直线BC 旋转一周所得旋转体为底面半径1=AC ，高3=BC 的圆锥中间挖掉一个半径33=r 的球．………………（8分） 所以，圆锥V V =球V -πππ27353334313132=⎪⎪⎭⎫ ⎝⎛⋅⋅-⋅⋅⋅=．…………（12分）20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．解：（1）若1=ω，则⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=6cos ,1πx a ，⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=6sin 2,2πx b ，由a ∥b 的充要条件知，存在非零实数λ，使得a b ⋅=λ，即⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛-⋅=⎪⎭⎫ ⎝⎛-=6cos 6sin 22πλπλx x ， 所以⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-6cos 6sin ππx x ，16tan =⎪⎭⎫ ⎝⎛-πx ，…………（3分）（以下有两种解法：）解法一：46πππ+=-k x ，Z k ∈，125ππ+=k x ，Z k ∈，32333333133164tan 125tan 125tan tan +=-+=-+=⎪⎭⎫ ⎝⎛+==⎪⎭⎫ ⎝⎛+=πππππk x ．…（6分） 解法二：323313316tan 6tan 16tan 6tan 66tan tan +=-+=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=ππππππx x x x ． 所以321313tan +=-+=x ．…………（6分）（2）⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+=6cos 6sin 226cos 6sin 22)(πωπωπωπωx x x x x f⎪⎭⎫⎝⎛-=32sin πωx ，…………（8分） 因为)(x f 的最小正周期为π，所以πωπ=22，1=ω，所以⎪⎭⎫ ⎝⎛-=32sin )(πx x f ，…………（10分）当⎥⎦⎤⎢⎣⎡∈2,0πx 时，⎥⎦⎤⎢⎣⎡-∈-32,332πππx ，…………（12分） 所以函数)(x f 的值域为⎥⎦⎤⎢⎣⎡-1,23．…………（14分）21．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分． 解：（1）由已知，当0=x 时，8)(=x C ，即85=k，所以40=k ，……（1分） 所以5340)(+=x x C ，…………（2分）又加装隔热层的费用为x x C 6)(1=．所以5380066534020)()(20)(1++=++⨯=+⋅=x x x x x C x C x f ，…………（5分） )(x f 定义域为]10,0[．…………（6分）（2）10380062103538003563538006538006)(-⨯≥-⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛++=++=x x x x x x x f70=，…………（10分）当且仅当⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+353800356x x ，18800352=⎪⎭⎫ ⎝⎛+x ，32035=+x ，即5=x 时取等号．…………（13分） 所以当隔热层加装厚度为5厘米时，总费用)(x f 最小．最小总费用为70万元．…（14分）22．（本题满分16分）本题共有3个小题，第1小题满分3分，第2小题满分7分，第3小题满分6分．解：（1）1=m 时，1)(2+=x x f ，因为01=a ，所以1)0()(12===f a f a ，2)(23==a f a ，5)(34==a f a ．…………（3分，每求对一项得1分）（2）m x x f +=2)(，则m a =2，m m a +=23，m m m m m m m a +++=++=2342242)(，…………（5分） 如果2a ，3a ，4a 成等比数列，则)2()(23422m m m m m m m +++=+，234523422m m m m m m m +++=++，0345=-+m m m ，…………（6分）因为02≠=m a ，所以012=-+m m ，251+-=m 或251--=m ．……（8分）当251+-=m 时，数列的公比2511223+=+=+==m m m m a a q ．……（9分） 当251--=m ，251-=q ．…………（10分） （3）1)(2-=x x f ，),0[+∞∈x ，所以1)(1+=-x x f （1-≥x ），……（11分）11=b ，121+=+n n b b ，所以1221+=+n n b b ，而121=b ，所以{}2n b 是以1为首项，1为公比的等比数列，n b n =2，…………（13分）所以2)1(21+=+++=n n n S n ，…………（14分） 由2010>n S ，即20102)1(>+n n ，解得63≥n ，所以所求的最小正整数n 的值是63．…………（16分） 23．（本题满分18分）本题共有3个小题，第1小题满分5分，第2小题满分6分，第3小题满分7分． 23．解：（1）设点),(y x P 是函数)(x f 图像上任意一点，P 关于点A 对称的点为),(y x P '''，则12='+x x ，22='+y y ，于是x x -='2，y y -='4，…………（2分） 因为),(y x P '''在函数)(x g 的图像上，所以2|2|24-'-'⋅--='x x a ay ，……（3分） 即x x a a y --⋅--=-244||，x x a a y -⋅+=2||，所以x x a a x f -⋅+=2)(||（或xx a a x f 2)(||+=）．………………（5分）（2）令t a x=，因为1>a ，0>x ，所以1>t ，所以方程m x f =)(可化为m tt =+2， 即关于t 的方程022=+-mt t 有大于1的相异两实数解．…………（8分）作2)(2+-=mt t t h ，则⎪⎪⎩⎪⎪⎨⎧>->>08120)1(2m m h ，…………（11分）解得322<<m ．所以m 的取值范围是)3,22(．…………（12分） （3）x x a ax g 2)(||+=，),2[∞+-∈x ．当0≥x 时，因为1>a ，所以1≥xa ，),3[3)(∞+∈=xa x g ，所以函数)(x g 不存在最大值．…………（13分）当02<≤-x 时，x xa a x g 12)(+=，令xt 2=，则t t t h x g 12)()(+==，⎪⎭⎫⎢⎣⎡∈1,12a t ， 当2212>a ，即421<<a 时，)(t h 在⎪⎭⎫⎢⎣⎡1,12a 上是增函数，存在最小值222a a +，与a 有关，不符合题意．…………（15分）当22102≤<a ，即42≥a 时，)(t h 在⎥⎦⎤⎢⎣⎡22,12a 上是减函数，在⎪⎪⎭⎫⎢⎣⎡1,22上是增函数，当22=t 即2log 21a x -=时，)(t h 取最小值22，与a 无关．…………（17分）综上所述，a 的取值范围是),2[4∞+．…………（18分）。

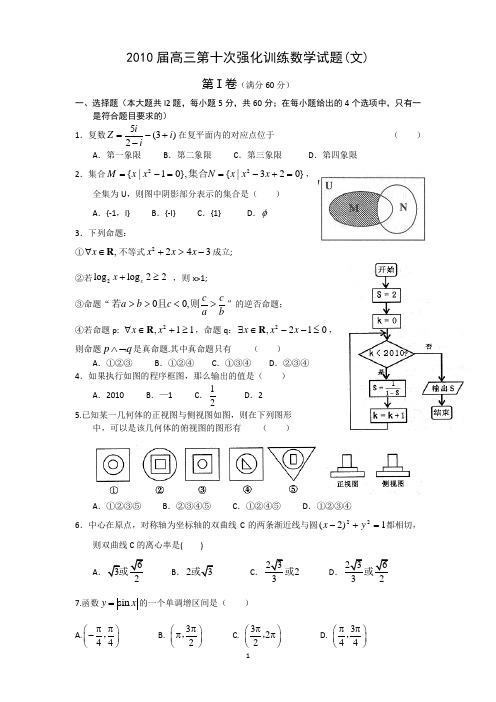
2010届高三第十次强化训练数学试题(文)第Ⅰ卷（满分60分）一、选择题（本大题共l2题，每小题5分，共60分；在每小题给出的4个选项中，只有一是符合题目要求的）1．复数5(3)2iZ ii=-+-在复平面内的对应点位于（）A．第一象限B．第二象限C．第三象限D．第四象限2．集合22{|10},{|320}M x x N x x x=-==-+=集合，全集为U，则图中阴影部分表示的集合是（）A．{-1，l} B．{-I} C．{1} D．φ3．下列命题：①,x∀∈R不等式2243x x x+>-成立;②若2log log22xx+≥，则x>1;③命题“00,c ca b ca b>><>若且则”的逆否命题；④若命题p: 2,11x x∀∈+≥R，命题q：2,210x x x∃∈--≤R，则命题p q∧⌝是真命题.其中真命题只有（）A．①②③B．①②④C．①③④D．②③④4．如果执行如图的程序框图，那么输出的值是（）A．2010 B．—1 C．12D．25.已知某一几何体的正视图与侧视图如图，则在下列图形中，可以是该几何体的俯视图的图形有（）A．①②③⑤B．②③④⑤C．①②④⑤D．①②③④6．中心在原点，对称轴为坐标轴的双曲线C的两条渐近线与圆1)2(22=+-yx都相切，则双曲线C的离心率是( )A．63或B．23或C．232或D．236或7.函数siny x=的一个单调增区间是（）A.ππ⎛⎫- ⎪44⎝⎭， B.3π⎛⎫π ⎪2⎝⎭， C.32π⎛⎫π⎪2⎝⎭， D.3ππ⎛⎫⎪44⎝⎭，8.设l m n ，，均互不重合的直线，其中m n ，在平面α内，则“l α⊥”是“l m ⊥且l n ⊥”的（ ）A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件9．若直线mx ＋ny ＝4和⊙O ∶422=+y x 没有交点，则过（m ，n ）的直线与椭圆14922=+y x 的交点个数（ ）A ．至多一个B ．0个C ．1个D ．2个10.如果实数x ，y 满足⎪⎩⎪⎨⎧≥≤-+≤+-,1,02553,034x y x y x 目标函数y kx z +=的最大值为12，最小值为3，那么实数k 的值为 （ ）A ．2B ．-2C ．51 D ．不存在11.若函数)(x f y =的导函数在区间[a ，b]上是先增后减的函数，则函数)(x f y =在区间[a ，b]上的的图象可能是（ ）12. 若)2(2)()(,0|,lg |)(ba fb f a f b a x x f +==<<=，则b 的值所在的区间为（ ）A ．（1，2）B ．（2，3）C ．（3，4）D ．（4，5） 二、填空题（本大题共4题，每小题5分，共20分） 13．不等式201xx -≥-的解集是 。

2010-高三数学试题D最大值是 ．9．（文）已知a 、b 、c 是锐角ABC ∆中角A 、B 、C 的对边，若3,4a b ==，ABC ∆的面积为33，则=c ．（理）如果函数||1|lg |)(-=x x f 在其定义域的某个子集(1,1)k k -+上不存在反函数，那么实数k的取值范围是 ． 10．（文）已知}221|{≤≤=x x A ，q px x x f ++=2)(和11)(++=xx x g 是定义在A 上的函数，当x 、0x A ∈时，有)()(0x f x f ≥，)()(0x g x g ≥，且)()(00x g x f =，则()f x 在A 上的最大值是 ． （理）若关于x 的方程0)5(6241=-+⋅-⋅+k k k x x 在区间[0,1]上有解，则实数k 的取值范围是 ． 11．（文）如果函数||1|lg |)(-=x x f 在定义域的某个子集)1,1(+-k k 上不存在反函数，那么实数k的取值范围是 ． （理）设()f x 是定义在R 上的奇函数，且对于任意的x R ∈，(1)(1)f x f x +=-恒成立. 当[0,1]x ∈时，()2f x x =. 若关于x 的方程()f x ax =有5个不同的解，则实数a 的取值范围是 . 12．（文）对于函数2()lg(1)f x x ax a =+--，给出下列命题：① 当0a=时，()f x 的值域为R ；② 当0a >时，()f x 在[2,)+∞上有反函数；③ 当01a <<时，()f x 有最小值；④ 若()f x 在[2,)+∞上是增函数，则实数a 的取值范围是[)4,-+∞.上述命题中正确的是 .（填上所有正确命题的序号） （理）设集合R A ⊆，如果R x ∈0满足：对任意0>a ，都存在A x ∈，使得a x x <-<||00，那么称0x 为集合A 的聚点。

2010年高考数学模拟试题—最后一套一、选择题（每小题5分，共60分）1．要得到x x y 2cos 2sin +=的图象，只需将x x y 2cos 2sin -=的图象（ ）．A ．向左平移8π B ．向右平移8πC ．向左平移4πD ．向右平移4π2．若等比数列}{n a 的前n 项和a S n n +=3，则a 为（ ）． A ．3 B ．1 C ．0 D ．-13．过点（2，1）的直线中，被圆04222=+-+y x y x 截得弦长为最大的直线方程是（ ）．A ．053=--y xB ．0773=-+y xC ．013=--y xD ．073=-+y x 4．已知复数)()i1i 1()i 1i 1()(*N ∈-+++-=n n f nn ，则集合)}(|{n f x x =中元素的个数是（ ）．A ．4B ．3C ．2D ．无数5．双曲线12222=-by a x 的一条准线被它的两条渐近线所截得的线段长度恰好等于它的一个焦点到一条渐近线的距离，则该双曲线的离心率为（ ）． A ．2 B ．3 C ．2 D ．56．设四面体ABCD 各棱长均相等，E 、F 分别为AC 、AD 的中点，则△BEF 在该四面体ABCD 上的射影是（ ）．A B C D 7．已知2sin 2sin 6=α，则)1tan()1tan(+-αα的值是（ ）．A ．57 B ．57- C ．75 D ．75-8．设二项式n x )21(+展开式的各项系数和为n a ，其二项式系数和为n b ，则nn n n n a b a b +-∞→l i m 等于（ ）．A ．1B ．-1C ．0D ．不存在9．A 、B 为两定点，3||=AB ，点P 到A 、B 的距离比为2，则点P 的轨迹是（ ）． A ．抛物线 B ．双曲线C ．半径为1.5的圆D ．半径为2的圆10．函数]4)3(lg[2+++=x k x y 的值域为R ，则实数k 的取值范围是（ ）． A ．17≤≤-k B ．7-≤k 或1≥k C ．71≤≤-k D ．7-<k 或1>k11．已知地球球心角1分所对球大圆弧长为1海里．在北纬45°圈上有甲、乙两地，甲地位于东经120°，乙地位于西经150°，则甲、乙两地的球面距离为（ ）． A ．5 400海里 B ．7 200海里 C ．4 800海里 D ．3 600海里12．6名同学报考A 、B 、C 三所院校，如果每一所院校至少有1人报考，则不同的报考方法共有（ ）．A ．216种B ．540种C ．729种D ．3 240种二、填空题（每小题4分，共16分） 13．给出下列四组命题：满足p 是q 的充分且必要条件的序号是________．14．定义在R 上的函数)(x f 满足关系式：2)21()21(=-++x f x f ，则+)81(f )82(f )87(f ++ 的值等于________． 15．在所有满足不等式组⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+00625y x y x y x ，，，的点（x ，y ）中，使目标函数y x k 86+=取得最大值的点的坐标是________．16．如图，已知电路中3个开关闭合的概率都是0.5，且是相互独立的，则灯亮的概率为________．三、解答题（第17～21题每题12分，第22题14分，共74分） 17．已知平面向量3(=a ，)1-，21(=b ，)23，若存在不同时为零的实数k 和t ，使x ＝a )3(2-+t b ，y ＝-k a ＋t b ，且x ⊥y ． （1）试求函数关系式)(t f k =； （2）求使0)(>t f 的t 的取值范围．18．如图，在棱长为a 的正方体1111D C B A ABCD -中，E 、F 分别为棱AB 和BC 的中点，EF 交BD 于H ．（1）求二面角B EF --1β的正切值；（2）试在棱B B 1上找一点M ，使⊥M D 1平面1EFB ，并证明你的结论； （3）求点1D 到平面1EFB 的距离．19．在不等边△ABC 中，设A 、B 、C 所对的边分别为a ，b ，c ，已知A 2sin ，B 2sin ，C 2sin 依次成等差数列，给定数列a A cos ，b B cos ，cC cos ． （1）试根据下列选项作出判断，并在括号内填上你认为是正确选项的代号： 数列a A cos ，b B cos ，cCcos （ ）． A ．是等比数列而不是等差数列 B ．是等差数列而不是等比数列C ．既是等比数列也是等差数列D ．既非等比数列也非等差数列 （2）证明你的判断．20．已知c bx ax x x f +++=23)(，在32-=x 与x ＝1时，都取得极值． （1）求a 、b 的值；（2）若对1[-∈x ，]2，2)(c x f <恒成立，求c 的取值范围．21．已知水渠在过水断面面积为定值的情况下，过水湿周越小，其流量越大． 现有以下两种设计，如图：图①的过水断面为等腰△ABC ，AB ＝BC ，过水湿周BC AB l +=1．图②的过水断面为等腰梯形ABCD ，AB ＝CD ，AD ∥BC ，∠BAD ＝60°，过水湿周CD BC AB l ++=2． 若△ABC 与梯形ABCD 的面积都为S ，图① 图② （1）分别求1l 和2l 的最小值；（2）为使流量最大，给出最佳设计方案．22．是否存在一个椭圆同时满足以下三个条件： （1）中心在坐标原点，焦点在x 轴上；（2）它的一个焦点为F ，M 是椭圆上任意一点，||MF 的最大值和最小值的几何平均数是2；（3）椭圆上存在着以直线y ＝x 为轴的两个对称点1M 和2M ，且3104||21=M M ． 若存在，请求出方程，若不存在，请说明理由．参考答案1．C 2．D 3．A 4．B 5．C 6．B 7．D 8．B 9．D 10．B 11．D 12．B 13．④ 14．7 15．（0，5） 16．0.625 17．（1）因为x ⊥y ，所以x ·y ＝0，即[a ＋)3(2-t b ]·（-k a ＋t b ）＝0．因为a ·b ＝0，a 2＝4，b 2＝1，所以0)3(42=-+-t t k ，即)3(412-=t t k ．（t ≠0） （2）由0)(>t f ，得0)3(412>-t t ，即0)3)(3(>-+t t t ，则03<<-t 或3>t 18．（1）连AC ，H B 1，则EF ∥AC ，因为AC ⊥BD ，所以BD ⊥EF ．因为B B 1⊥平面ABCD ，所以H B 1⊥EF ，所以∠HB B 1为二面角B EF B --1的平面角．在Rt △BH B 1中，a B B =1，a BH 42=．所以22tan 11==∠BH B B HB B ． （2）在棱B B 1上取中点M ，连M D 1，因为EF ⊥平面11BDD B ，所以EF ⊥M D 1．在正方形C C BB 11中，因为M ，F 分别为1BB ，BC 的中点，所以F B 1⊥M C 1．又因为11C D ⊥平面11B BCC ，所以F B 1⊥11C D ，所以F B 1⊥M D 1，所以M D 1⊥平面1EFB ． （3）设M D 1与平面1EFB 交于点N ，则N D 1为点1D 到平面1EFB 的距离．在Rt △11D MB 中，M D N D B D 11211⋅=．因为a B D 211=，a M D 231=，所以a M D B D N D 3412111==，故点1D 到平面1EFB 的距离为a 3419．（1）B （2）因为A 2sin 、B 3sin 、C 2sin 成等差数列，所以C A B 222sin sin sin 2+=，所以2222c a b +=．又abc b c a b B 2cos 222-+=，abca cb a A 2cos 222-+=， abcc b a c C 2cos 222-+=．显然c C a A b B cos cos cos 2+=，即a A cos 、b B cos 、c C cos 成等差数列．若其为等比数列，有cCb B a A co s co s co s ==，所以C B A t an t an t an ==，C B A ==，与题设矛盾20．（1）由题设023)(2=++='b ax x x f 的两根为32-和1，由韦达定理，得⎪⎪⎩⎪⎪⎨⎧⨯-=+-=-，，132313232b a 即21-=a ，2-=b ． （2）由（1）知c x x x x f +--=221)(23，且当1[-∈x ，)32-时，0)(>'x f ，32(-∈x ，)1时0)(<'x f ，1(∈x ，]2时，0)(>'x f ，所以当32-=x 时，)(x f 有极大值c +2722．又c f +=2)2(，即当1[-∈x ，]2时，)(x f 的最大值为c f +=2)2(．因为对1[-∈x ，]2，2)(c x f <恒成立，所以c c +>22，解得1-<c 或2>c ．故c 的取值范围是（-∞，-1）∪（2，＋∞） 21．（1）在图①中，设∠θ=ABC ，AB ＝BC ＝a ．则θs in 212a S =，由于S 、a 、θsin 皆为正值，可解得S Sa 2sin 2≥=θ．当且仅当1sin =θ，即θ＝90°时取等号．所以S a l 2221≥=，1l 的最小值为S 22．在图②中，设AB ＝CD ＝m ，BC ＝n ，由∠BAD ＝60°可求得AD ＝m ＋n ，m n m n S 23)(21⋅++=，解得232m m S n -=．m n m l 222=+= S S mm S m m S 432322332232=≥+=-+，2l 的最小值为S 432．当且仅当2332m m S =，即334S m =时取等号． （2）由于432>，则2l 的最小值小于1l 的最小值．所以在方案②中当2l 取得最小值时的设计为最佳方案22．存在，方程为14522=+y x ．假设存在)0(12222>>=+b a b y a x 满足条件．则222))((==-+b c a c a ，所以b ＝2．所以)2(14222>=+a y a x 为其方程．设1M 、2M 所在直线方程为m x y +-=，代入椭圆方程得：042)4(222222=-+-+a m a mx a x a ．则2221042a ma x x x +=+=．20044a m m x y +=+-=．因为（0x ，0y ）在直线y ＝x 上，从而222444a m a m a +=+．因为42>a ，所以m ＝0，从而021=+x x ，222144aa x x +-=．||21M M 310441624)(112221221=+=-++=a a x x x x ．解得52=a ，经检验符合条件．故椭圆的方程为14522=+y x ．。

大冈中学2010届高三数学小题训练1（09.12.14）1．复数i i 4321+-在复平面上对应的点位于第 象限.2．已知集合{}11M =-，，11242x N x x +⎧⎫=<<∈⎨⎬⎩⎭Z ，，则M N = .3．命题“0,x ∀>都有sin 1x ≥-”的否定： .4．右图程序运行结果是 ______________ 5．设O OM ),1,0(),21,1(==为坐标原点， 动点),(y x p 满足01,01OP OM OP ON ≤⋅≤≤⋅≤ ,则 z y x =-的最小值是 ．6．函数1)1(log +-=x y a (01)a a >≠且，的图象恒过 定点A ，若点A 在一次函数n mx y +=的图象上，其中0mn >，则12m n+的最小值为 ．7．设O 是△ABC 内部一点，且AOC AOB ∆∆-=+与则,2的面积之比为8．不等式322+-x x 122--≤a a 在R 上的解集是∅，则实数a 的取值范围是9．在样本的频率分布直方图中,共有4个小长方形,这4个小长方形的面积由小到大构成等比数列}{n a ,已知122a a =,且样本容量为300,则小长方形面积最大的一组的频数为10．已知数列{n a }、{n b }都是等差数列，n n T S ,分别是它们的前n 项和，并且317++=n n T S n n ，则1612108221752b b b b a a a a ++++++=11．实数,x y 满足tan ,tan x x y y ==，且x y ≠，则sin()sin()x y x y x y x y+--=+-12．已知04,k <<直线1:2280l kx y k --+=和直线222:2440l x k y k +--=与两坐标轴；围成一个四边形，则使得这个四边形面积最小的k 值为13. 在数列{}n a 中，11111,(1)2n n n n a a a n ++==++（I ）设n n a b n=，求数列{}n b 的通项公式 （II ）求数列{}n a 的前n 项和n S。

2010年江苏高考数学模拟试卷(3)一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应的位置上. 1. 若集合M={y|y=3-x},P={y|y=3x-3}, 则M∩P=2. a0在x∈\上有解的概率为11. 若实数x,y满足x≤1,|y|≤x,x2+y2-4x+2≥0,在平面直角坐标系中,此不等式组表示的平面区域的面积是12.已知函数f(x)=ax2-(a+2)x+1.若a为整数,且函数f(x)在(-2,-1)内恰有一个零点,则a的值为 .13. 已知椭圆的中心在坐标原点,焦点在x轴上,以其两个焦点和短轴的两个端点为顶点的四边形是一个面积为4的正方形,设P为该椭圆上的动点,C、D的坐标分别是(-2,0),(2,0),则PC&#8226;PD的最大值为14. 已知实数x、s、t满足:8x+9t=s,且x>-s,则x2+(s+t)x+st+1x+t 的最小值为 .二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程或演算步骤15.(本小题满分14分)已知点A(1,0),B(0,1),C(2sinθ,cosθ).(1)若|AC|=|BC|,求tanθ的值;(2)若(OA+2OB)&#8226;OC=1,其中O为坐标原点,求sin2θ的值16.(本小题满分14分)如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD、AB的中点.(1)求证:EF∥平面CB1D1;(2)求证:平面CAA?┆?1C1⊥平面CB1D1;(3)如果AB=1,一个动点从点F出发在正方体的表面上依次经过棱BB1、B1C1、C1D1、D1D、DA上的点,最终又回到点F,指出整个路线长度的最小值并说明理由.17.(本小题满分14分)经市场调查,某旅游城市在过去的一个月内(以30天计),旅游人数f(t)(万人)与时间t(天)的函数关系近似满足f(t)=4+1t,人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)=115-|t-15|.(Ⅰ)求该城市的旅游日收益w(t)(万元)与时间t(1≤t≤30,t∈N)的函数关系式;(Ⅱ)求该城市旅游日收益的最小值(万元).18.(本小题满分16分)如图,已知A,B是中心在原点O,焦点在x轴上,离心率e=12的椭圆的左顶点和上顶点,F1,F2是左、右焦点,点P在椭圆上,且在x轴上方,PF2垂直于x轴,△ABP的面积为32(3-1).(1)求椭圆方程;(2)我们把以O为圆心,OA为半径的圆称为“椭圆的大圆”.若直线m 是椭圆的左准线,Q是直线m上一动点,以Q为圆心,且经过F2的圆与该椭圆的大圆相交于M,N两点,求证:直线MN过一定点,并求出定点坐标;(3)在(2)中,若将条件“直线m是椭圆的左准线”改为“直线m过A 点且平行于椭圆的准线”,是否有类似的结论?根据你的推理,给出一个更为一般的结论(无需证明).第18题图19.(本小题满分16分)已知数列{an}是以d为公差的等差数列,数列{bn}是以q为公比的等比数列.(Ⅰ)若数列{bn}的前n项和为Sn,且a1=b1=d=2,S3 (Ⅱ)在(Ⅰ)的条件下,试问数列{bn}中是否存在一项bk,使得bk恰好可以表示为该数列中连续p(p∈N,p≥2)项的和?请说明理由;20.(本小题满分16分)已知函数f(x)=ax3+|x-a|(a∈R).(1)给出一个实数a,使得函数f(x)在(-∞,0]上单调减,在[0,+∞)上单调增.(2)若0 (3)求证:对任意的实数a,存在x0,恒有f(x0)≠0,并求出符合该特征的x0的取值范围.附加题部分(本部分满分40分,考试时间30分钟)21.[选做题] 在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.A.(选修4―1:几何证明选讲)如图,已知OA、OB是⊙O的半径,且OA⊥OB,P是线段OA上一点,直线BP交⊙O于点Q,过Q作⊙O的切线交直线OA于点E,求证:∠OBP+∠AQE=45°.B.(选修4―2:矩阵与变换)给定矩阵 A=2 13 0,求A的特征值λ1、λ2 及对应的特征向量a1、a2 .C.(选修4―4:坐标系与参数方程)已知直线l的参数方程:x=ty=1+2t(t为参数)和圆C的极坐标方程:ρ=22sin(θ+π4).(Ⅰ)将直线l的参数方程化为普通方程,圆C的极坐标方程化为直角坐标方程;(Ⅱ)判断直线l和圆C的位置关系.D.(选修4―5:不等式选讲)已知函数f(x)=|x-1|+|x-2|. 若不等式|a+b|+|a-b|≥|a|f(x)(a≠0,a,b∈R)恒成立,求实数x的范围.[必做题] 第22、23题,每小题10分,计20分.请把答案写在答题纸的指定区域内.22.(本小题满分10分)如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=π4, OA⊥底面ABCD, OA=2,M为OA的中点.(Ⅰ)求异面直线AB与MD所成角的大小;(Ⅱ)求点B到平面OCD的距离.23. (本小题满分10分)点Pn(xn,yn)在曲线C:y=e-x上,曲线C在Pn处的切线ln与x轴相交于点Qn(xn+1,0),直线tn+1:x=xn+1与曲线C相交于点Pn+1(xn+1,yn+1),(n=1,2,3,…).由曲线C和直线ln,tn+1围成的图形面积记为Sn,已知x1=1.(1)证明:xn+1=xn+1;(2)求Sn关于n的表达式;(3)若数列{Sn}的前n项之和为Tn,求证:Tn+1Tn0}2. 充分不必要3. -124. 45. -1+526. 77. 38. 1209. 1310. 1211. 2-π212. -113. 414. 6二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程或演算步骤15.解:⑴∵A(1,0),B(0,1),C(2sinθ,cosθ)∴AC=(2sinθ-1,cosθ),BC=(2sinθ,cosθ-1)?ぁ?|AC|=|BC|∴(2sinθ-1)2+co s2θ=4sin2θ+(cosθ-1)2 ∴2sinθ=cosθ,∵cosθ≠0,∴tanθ=12(2)∵OA=(1,0),OB=(0,1),OC=(2sinθ,cosθ)∴OA+2OB=(1,2),∵(OA+2OB)&#8226;OC=1∴2sinθ+2cosθ=1,∴sinθ+cosθ=12,∴(sinθ+cosθ)2=14,∴sin2θ=-3416.(1)证明:连结BD.在正方体AC1中,对角线BD//B1D1.又∵E、F为棱AD、AB的中点,∴EF∥BD.∴EF∥B1D1.又B1D1?计矫?CB1D1,EF?て矫?CB1D1,∴ EF∥平面CB1D1.(2)证明:∵ 在正方体AC1中,AA1⊥平面A1B1C1D1,而B1D1?计矫?A1B1C1D1,∴ AA1⊥B1D1.又∵在正方形A1B1C1D1中,A1C1⊥B1D1,∴ B1D1⊥平面CAA1C1.又∵ B1D1?计矫?CB1D1,∴平面CAA1C1⊥平面CB1D1.(3)最小值为 32.如图,将正方体六个面展开成平面图形,从图中F到F,两点之间线段最短,而且依次经过棱BB1、B1C1、C1D1、D1D、DA上的中点,所求的最小值为 32.17.解:(Ⅰ)由题意得,w(t)=f(t)&#8226;g(t)=(4+1t)(115-|t-15|)(Ⅱ)因为w(t)=(4+1t)(t+100),(1≤t0)由A(-2c,0),B(0,3c),P(c,3c2),则直线AP方程:y=12(x+2c),令x=0得y=c,S?│?ABP=12×(3c-c)&#8226;(c+2c)=3(3-1)2c2=3(3-1)2,则c=1,则椭圆方程为x24+y23=1;(2)依题意,直线m的方程:x=-4,设Q(-4,t),F2(1,0),则圆Q:(x+4)2+(y-t)2=25+t2,又圆O的方程:x2+y2=4两式相减,得直线MN的方程:8x-2ty-5=0,显然,直线MN过定点(58,0)(3)当直线m的方程变为:x=-2,设Q(-2,t),F2(1,0),则圆Q:(x+2)2+(y-t)2=9+t2,又圆O的方程:x2+y2=4两式相减,得直线MN的方程:4x-2ty-1=0,显然,直线MN过定点(14,0);推广(1):若直线m平行于椭圆的准线,Q是直线m上一动点,且以Q为圆心,且经过F2的圆与该椭圆的大圆相交于M,N两点,则直线MN过x轴上一定点;推广(2):若Q是一条定直线m上一动点,且以Q为圆心,且经过F2的圆与该椭圆的大圆相交于M,N两点,则直线MN过一定点.(注:只要求写出一种推广,且不要求在推广结果中算出定点坐标.)19.解:(Ⅰ)由题意知,an=2n,bn=2&#8226;qn-1,所以由S3 得b1+b2+b3 解得1bm+p-12k>2m+p-1k>m+p-1k≥m+p(*)又bk=2k=bm+bm+1+bm+2+…+bm+p-1=2m+2m+1+…+2m+p-1=2m(2p-1)2-1 =2m+p-2ma时,f′(x)=3ax2+1,①当0 ②当13 在[-13a,a]上单调减,在[a,1]上单调增,由于f(-13a)>f(-1)=f(1),则在[-1,1]上f(x)?┆?max=f(-13a)=a+2313a;③当313 在[-13a,13a]上单调减,在[13a,a]上单调增,在[a,1]上单调增,则在[-1,1]上f(x)?┆?max=f(-13a)=a+2313a;综合①②③有:当0 当13 (3)(Ⅰ)当a=0时,f(x)=|x|,方程f(x)=|x|=0只有0根;(Ⅱ)当a>0时,方程f(x)=ax3+|x-a|=0没有0根和正根,当a>0,x0 x3+10时,f(x)=ax3+x-a,由方程f(x)=ax3+x-a=0得a=-xx3-1,则x>0a=-xx3-10,得x>1;综上可知,对任意的实数a,存在x0∈[-1,0)∪(0,1],恒有f(x0)≠0.注:本题也可以用数形结合的思想来做.当a=0时,f(x)=|x|,方程f(x)=|x|=0只有0根;当a>0时,方程f(x)=ax3+|x-a|=0要有解也只能是负解,f(x)=ax3-x+a=0即x3+1=1ax,用数形结合(图1)寻找负解,发现二曲线交点横坐标x1;以下同上图1 图2附加题部分21.A.解:证:连结AB,则∠AQE=∠ABP, 而OA=OB,所以∠ABO=45°所以∠OBP+∠AQE=∠OBP+∠ABP=∠ABO=45°B.解:设A的一个特征值为λ,由题意知:λ-2 -1-3 λ=0,所以(λ-2)&#8226;λ-3=0,即λ1=-1.λ2=3当λ1=-1时,由2 13 0xy=-1xy,得A属于特征值-1的特征向量a1=1-3 当λ2=3时,由2 13 0xy=3xy,得A属于特征值3的特征向量a2=11C.解:(Ⅰ)消去参数t,得直线l的普通方程为y=2x+1ρ=22(sinθ+π4)即ρ=2(sinθ+cosθ),两边同乘以ρ得ρ2=2(ρsinθ+ρcosθ),消去参数θ,得⊙C的直角坐标方程为:(x-1)2+(x-1)2=2(Ⅱ)圆心C到直线l的距离d=|2-1+1|22+12=255(e-1)n+e下用数学归纳法(或用二项式定理,或利用函数的单调性)等方法来证明en+1>(e-1)n+e(略)希望以上资料对你有所帮助，附励志名言3条：1、生命对某些人来说是美丽的，这些人的一生都为某个目标而奋斗。