工程力学第16章(压杆稳定问题)
- 格式:ppt
- 大小:1.69 MB
- 文档页数:35





压杆稳定问题中,欧拉公式成立的条件以压杆稳定问题中,欧拉公式成立的条件为题,我们来探讨一下这个问题。
压杆稳定问题是工程力学中的一个经典问题,研究的是在受到外力作用下,压杆是否会发生失稳。
而欧拉公式则是描述了在何种条件下,压杆会发生失稳的公式。
我们来看一下欧拉公式的表达式。
欧拉公式可以用数学语言来表示为Fcr = π²EI / L²,其中Fcr表示压杆的临界压力,E表示杨氏模量,I表示截面惯性矩,L表示杆长。
这个公式告诉我们,只有当外力超过了临界压力时,压杆才会发生失稳。
那么,欧拉公式成立的条件是什么呢?欧拉公式的推导是基于一些假设条件的。
这些条件包括:杆件是理想的无限细杆,杆的截面是均匀的,杆材的弹性模量是常数,杆件的边界条件是完美固定或者挠度为零。
只有在满足这些条件的情况下,欧拉公式才能成立。
欧拉公式的成立还与杆件的形状有关。
对于不同形状的杆件,其欧拉公式的形式也会有所不同。
例如,对于长方形截面的杆件,欧拉公式可以写成Fcr = π²Ebh² / L²,其中b和h分别表示杆件的宽度和高度。
对于圆形截面的杆件,欧拉公式可以写成Fcr = π²Eπr⁴ / L²,其中r表示杆件的半径。
欧拉公式还要求杆件处于稳定的静力平衡状态。
也就是说,在外力作用下,杆件的挠度要小到可以忽略不计。
如果杆件的挠度过大,那么欧拉公式就不再适用。
欧拉公式成立的条件还包括杆件的材料特性。
杆件的弹性模量E是杆件材料的一个重要参数,它描述了杆件材料的刚度。
当杆件的材料刚度较大时,欧拉公式更加准确。
欧拉公式成立的条件包括:杆件是理想的无限细杆,杆的截面是均匀的,杆材的弹性模量是常数,杆件的边界条件是完美固定或者挠度为零;杆件处于稳定的静力平衡状态;杆件的形状和材料特性。
在工程实践中,我们经常使用欧拉公式来计算杆件的临界压力,以确定杆件是否会发生失稳。
通过合理选择杆件的形状和材料,我们可以满足欧拉公式成立的条件,从而保证杆件的稳定性。



一、单选题1、压杆一般分为三种类型,它们是按压杆的()。
A.惯性半径分B.杆长分C.柔度分D.杆端约束情况分正确答案:C2、细长压杆,若其长度系数增加一倍,则()。
A.Pcr增加一倍B.Pcr增加到原来的4倍C.Pcr为原来的二分之一倍D.Pcr为原来的四分之一倍正确答案:D3、下列结论中正确的是()。
①若压杆中的实际应力不大于该压杆的临界应力,则杆件不会失稳;②受压杆件的破坏均由失稳引起;③压杆临界应力的大小可以反映压杆稳定性的好坏;④若压杆中的实际应力大于scr=πE2/λ2,则压杆必定破坏。
A.①+②B.②+④C.①+③D.②+③正确答案:C4、压杆临界力的大小()。
A.与压杆所承受的轴向压力大小有关B.与压杆的柔度大小有关C.与压杆材料无关D.与压杆的柔度大小无关正确答案:B5、两端铰支的圆截面压杆,若λp=100,则压杆的长度与横截面直径之比l/d在时,才能应用欧拉公式()。
A.25B.50C.400D.200正确答案:A6、若两根细长压杆的惯性半径i相等,当()相同时,它们的柔度相等。
①杆长;②约束类型;③弹性模量;④外部载荷A.①+②B.①+②+③C.①+②+④D.①+②+③+④正确答案:A7、a、b两根都是大柔度杆,材料、杆长和横截面形状大小都相同,杆端约束不同。
其中a为两端铰支,b为一端固定,一端自由。
那么两杆临界力之比应为()。
A.4B.1/4C.2D.1/2正确答案:A8、提高水稻抗倒伏性能的可能措施包括()。
A.选用茎秆强壮品种B.选用节间较短的矮秆品种C.使用植物生长调节剂,以调控节间长度与株高等D.以上都是正确答案:D9、圆形压杆和矩形压杆在稳定性校核时有何区别()。
A.圆形压杆不需要考虑失稳方向性,而矩形压杆需要考虑B.圆形压杆需要考虑失稳方向性,而矩形压杆不需要考虑C.两者都不需要考虑D.两者都需要考虑正确答案:A10、压杆合理设计措施包括:①合理选用材料;②合理选择截面;③合理安排压杆约束与杆长()。

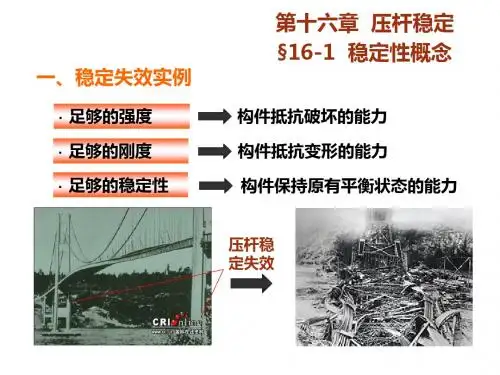
第16章压杆稳定16.1 压杆稳定性的概念在第二章中,曾讨论过受压杆件的强度问题,并且认为只要压杆满足了强度条件,就能保证其正常工作。
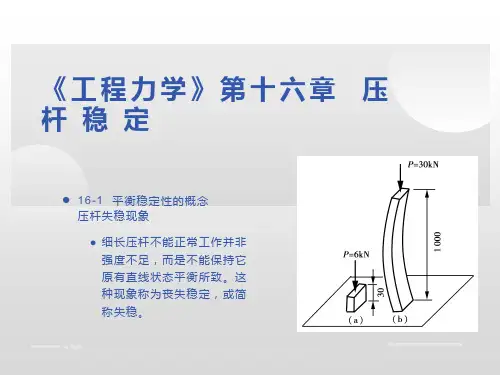
但是,实践与理论证明,这个结论仅对短粗的压杆才是正确的,对细长压杆不能应用上述结论,因为细长压杆丧失工作能力的原因,不是因为强度不够,而是由于出现了与强度问题截然不同的另一种破坏形式,这就是本章将要讨论的压杆稳定性问题。
当短粗杆受压时(图16-1a),在压力F由小逐渐增大的过程中,杆件始终保持原有的直线平衡形式,直到压力F达到屈服强度载荷F s(或抗压强度载荷F b),杆件发生强度破坏时为止。
但是,如果用相同的材料,做一根与图16-1a所示的同样粗细而比较长的杆件(图16-1b),当压力F比较小时,这一较长的杆件尚能保持直线的平衡形式,而当压力F逐渐增大至某—数值F1时,杆件将突然变弯,不再保持原有的直线平衡形式,因而丧失了承载能力。
我们把受压直杆突然变弯的现象,称为丧失稳定或失稳。
此时,F1可能远小于F s(或F b)。
可见,细长杆在尚未产生强度破坏时,就因失稳而破坏。
图16-1失稳现象并不限于压杆,例如狭长的矩形截面梁,在横向载荷作用下,会出现侧向弯曲和绕轴线的扭转(图16-2);受外压作用的圆柱形薄壳,当外压过大时,其形状可能突然变成椭圆(图16-3);圆环形拱受径向均布压力时,也可能产生失稳(图16-4)。
本章中,我们只研究受压杆件的稳定性。
图16-3所谓的稳定性是指杆件保持原有直线平衡形式的能力。
实际上它是指平衡状态的稳定性。
我们借助于刚性小球处于三种平衡状态的情况来形象地加以说明。
第一种状态,小球在凹面的O点处于平衡状态,如图16-5a所示。
先用外加干扰力使其偏离原有的平衡位置,然后再把干扰力去掉,小球能回到原来的平衡位置。
因此,小球原有的平衡状态是稳定平衡。
第二种状态,小球在凸面上的O点处于平衡状态,如图16-5c所示。
当用外加干扰力使其偏离原有的平衡位置后,小球将继续下滚,不再回到原来的平衡位置。