工程力学 第二版 (范钦珊 唐静静 著) 高等教育出版社 课后答案 第11章 压杆的稳定性问题
- 格式:pdf
- 大小:385.58 KB
- 文档页数:10

力学习题剖析目录第01 章物理学、力学、数学 (01)第02 章质点运动学 (05)第03 章动量定理及其守恒定律 (15)第04 章动能和势能 (28)第05 章角动量及其规律 (38)第06 章万有引力定律 (42)第07 章刚体力学 (45)第08 章弹性体的应力和应变 (56)第09 章振动 (60)第10 章波动 (68)第11 章流体力学 (75)大学物理学院1 + x 2xx3 x xa ∫ a dx 3 2 ∫ 2 (x 3 − 3x +1)dx = x 3dx − 3 dx = 1 x 4 − 3 2+ x + c 1+ x 21+ x 21+ x 2dh = d (102 −10− 4 x 2 + 5 ×10−7 x 4 ) = 2 ×10−6 x 3 − 2 ×10−4 x dx =1 (ax + b ) −1 /2 d (ax + b ) = 2 x x ∫ 2x x 2 2 41. 求下列函数的导数⑴y = 3x 2− 4x + 10⑵ y = 1/+ 7 s in x + 8 c os x −100⑴ ∫( x 3− 3x +1)dx⑵∫ (2x+ x 2 )dx⑶∫ ( 3 + 2e x− 1 )dx⑷∫ (sin x − cos x )dx⑶ y = (ax + b ) /( a + bx ) ⑷ y = sin ⑸ x 21+ x ⑹ ∫ sin( ax + b )dx⑸ y = e sin x⑹ y = e− x+ 100x⑺∫e − 2 x dx 2 ⑻ ⑼ ∫ sin x cos xdx ⑽ ∫ xe dx 解:⑴ y ' = 6x − 4(11) ∫ cos 2xdx(12)∫ ln x dx⑵ y ' = −1/( 2x x ) + 7 cosx − 8 sin x 解:⑶ y ' = (a 2 − b 2 ) /( a + bx ) 2⑷ y ' = cos(1+ x 2 )1/ 2· 1(1+ x 2 )−1 / 2· 2x∫ ∫ ∫ ∫ 4 2 2= x c os /⑵ ∫ (2x + x 2 )dx = ∫ 2xdx + ∫x 2 dx = 2xln 2 + 1 x 3+ c ⑸ y ' = e sin x cos x⑶ ∫ ( 3 + 2e x − 1 dx = 3∫ dx+ 2∫ e xdx − ∫ x − 3/ 2 dx ⑹ y ' = e − x (−1) + 100 = 100 − e − x= 3ln x + 2e x c⑷ ∫(sin x − cos x )dx = ∫sin xdx − ∫ cos xdx = − c os x − sin x + c 2.已知某地段地形的海拔高度 h 因水平坐标 x 而变,h=100-⑸ ∫ x 2 dx = ∫ 1+ x2−1dx = ∫ dx − ∫dx = x − arctgx + c 0.0001x 2(1-0.005x 2),度量x 和 h 的单位为米。
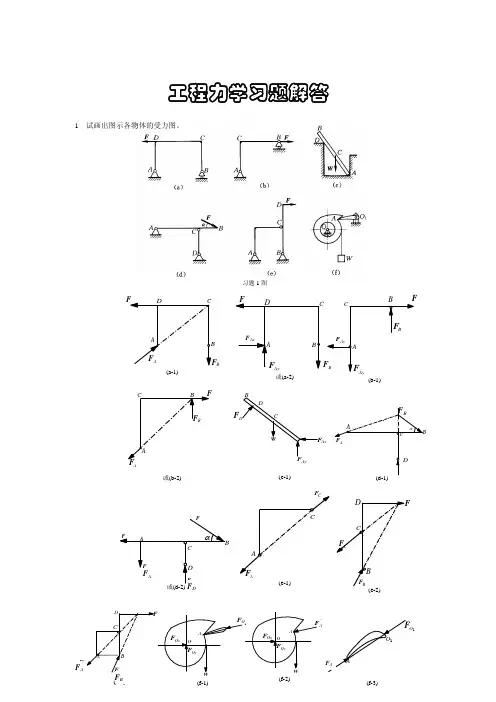

(a) (b) 习题1-1图 (a) (b) 习题1-2图FD R F AC BD Ax F AyF(a-1) Ay F F B C A AxF 'F C (a-2)C D C F D R(a-3)AxF D R F FA C BD Ay F(b-1) 1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一方F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
解:〔a 〕,图〔c 〕:11 sin cos j i F ααF F += 分力:11 cos i F αF x = , 11 sin j F αF y = 投影:αcos 1F F x = , αsin 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
〔b 〕,图〔d 〕:分力:22)tan sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y =投影:αcos 2F F x = , )cos(2αϕ-=F F y 讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 、b 两情形下各物体的受力图,并进行比较。
比较:图〔a-1〕与图〔b-1〕不同,因两者之F R D 值大小也不同。
1-3 试画出图示各物体的受力图。
1y F x 1x F 1y F α1x F y F 〔c 〕2F 2y F 2y 2x 2x F 2y F F 〔d 〕习题1-4图习题1-3图1-4 图a 所示为三角架结构。
力F 1作用在B 铰上。
杆AB 不计自重,杆BD 杆自重为W 。
试画出图b 、c 、d 所示的隔离体的受力图,并加以讨论。
F AxF AyF D C B A B F 或(a-2) F B B AF D C A (a-1) B F AxF A Ay F B C(b-1)W F B DC Ay F AxF (c-1) F A F C BBF A或(b-2) αD A F A B CB FC F C AA F (e-1) Ax F A Ay F D F D C αF或(d-2)B F FCD B OOx F OyF W 1O F A(f-1)FA F D C AB B F (e-3) F AO Ox F OyF AW (f-2) A F 1O F A 1O (f-3) c F F A F D F B F A F AAx F C 'Cx F 'BF B AyF 'F Cy A(b-3)E F D F E D (a-3) CF F CE 'F E(a-2) 习题1-5图E EF B B F (b-2)CxF C CyF W T(b-1) B F B C 'C F D 'D F Ax F Ay F A (a-1)1-5 试画出图示结构中各杆的受力图。

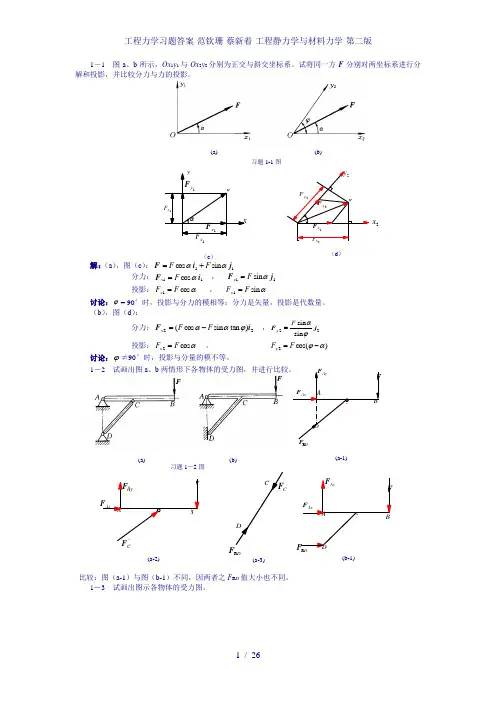
(a) (b) 习题1-1图 (a) (b) 习题1-2图FD R F ACBDAx F AyF(a-1) Ay F F B C A Ax F 'F C(a-2)C D F D R F(a-3)AxF F FA C BD Ay F(b-1) 1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一方F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
解:(a ),图(c ):11 sin cos j i F ααF F +=分力:11 cos i F αF x = , 11 sin j F αF y = 投影:αcos 1F F x = , αsin 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b ),图(d ):分力:22)tan sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y =投影:αcos 2F F x = , )cos(2αϕ-=F F y 讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 、b 两情形下各物体的受力图,并进行比较。
比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
1-3 试画出图示各物体的受力图。
1y F x 1F 1y F α1x F y F (c )x F 2y F 2y 2x 2x F 2y F F (d )习题1-3图1-4 图a 所示为三角架结构。
力F 1作用在B 铰上。
杆AB 不计自重,杆BD 杆自重为W 。
试画出图b 、c 、d 所示的隔离体的受力图,并加以讨论。
F Ax F AyF D C B A B F 或(a-2) F B F A F D C A (a-1) B F AxF AAy F C(b-1)W F B DC Ay F F (c-1) FF C B B F A或(b-2) αD A F A BCBFC F C A A F (e-1) Ax F A Ay FD F D C αF或(d-2)BF F C D B OOx F OyF W 1O F A(f-1)FA F D C AB B F 'F A O Ox F OyF AW (f-2) A 1F A 1O (f-3) c F F A F D F B F AF AAx F C 'CxF 'B F B Ay F 'F CyA (b-3)EF D F E D (a-3) C F F CE 'F E (a-2) 习题1-5图E EF B B F(b-2)Cx F C CyF W T(b-1) AyF Ax F 'BF 'C F C 'D F A D D F E F 'E F E BBF C F C D(c) F A G B F B C 'CF D 'D F Ax F AyF A1-5 试画出图示结构中各杆的受力图。

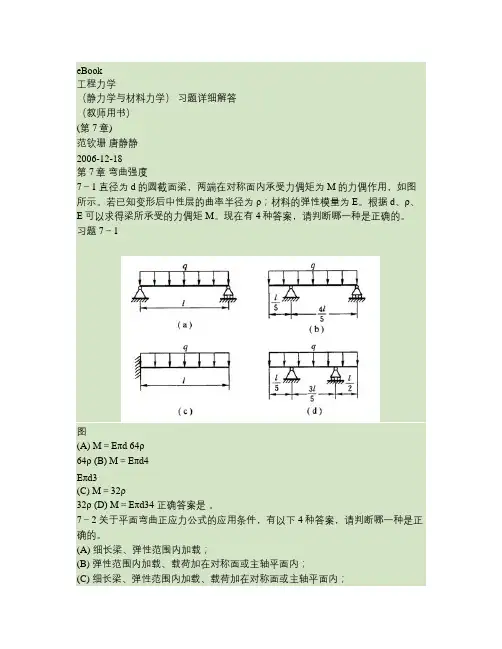
eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第7章)范钦珊唐静静2006-12-18第7章弯曲强度7-1 直径为d的圆截面梁,两端在对称面内承受力偶矩为M的力偶作用,如图所示。
若已知变形后中性层的曲率半径为ρ;材料的弹性模量为E。
根据d、ρ、E可以求得梁所承受的力偶矩M。
现在有4种答案,请判断哪一种是正确的。
习题7-1图(A) M=Eπd 64ρ64ρ (B) M=Eπd4Eπd3(C) M=32ρ32ρ (D) M=Eπd34 正确答案是。
7-2 关于平面弯曲正应力公式的应用条件,有以下4种答案,请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载;(B) 弹性范围内加载、载荷加在对称面或主轴平面内;(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内;(D) 细长梁、载荷加在对称面或主轴平面内。
正确答案是 C _。
7-3 长度相同、承受同样的均布载荷q作用的梁,有图中所示的4种支承方式,如果从梁的强度考虑,请判断哪一种支承方式最合理。
l 5习题7-3图正确答案是7-4 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为mm。
求:梁的1-1截面上A、 2B两点的正应力。
习题7-4图解:1. 计算梁的1-1截面上的弯矩:M=−⎜1×10N×1m+600N/m×1m×2. 确定梁的1-1截面上A、B两点的正应力:A点:⎛⎝31m⎞=−1300N⋅m 2⎟⎠⎛150×10−3m⎞−20×10−3m⎟1300N⋅m×⎜2My⎝⎠×106Pa=2.54MPa(拉应力)σA=z=3Iz100×10-3m×150×10-3m()12B点:⎛0.150m⎞1300N⋅m×⎜−0.04m⎟My⎝2⎠=1.62×106Pa=1.62MPa(压应力)σB=z=3Iz0.1m×0.15m127-5 简支梁如图所示。
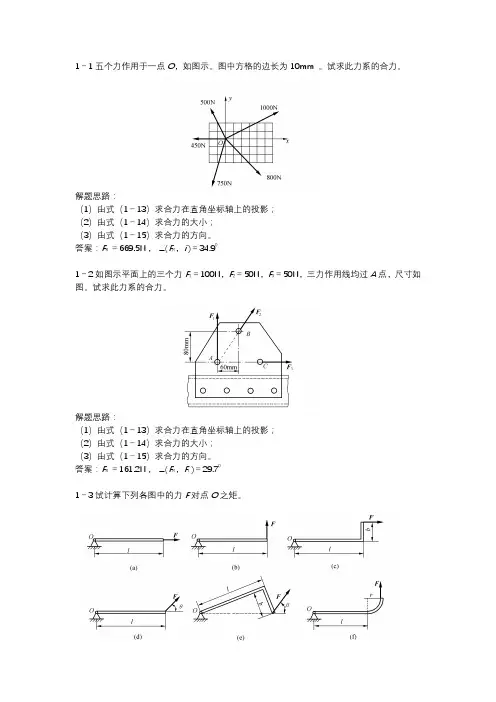
1-1五个力作用于一点O,如图示。
图中方格的边长为10mm 。
试求此力系的合力。
解题思路:(1)由式(1-13)求合力在直角坐标轴上的投影;(2)由式(1-14)求合力的大小;(3)由式(1-15)求合力的方向。
答案:F R =669.5N , ∠(F R,i )=34.901-2如图示平面上的三个力F1=100N,F2=50N,F3=50N,三力作用线均过A点,尺寸如图。
试求此力系的合力。
解题思路:(1)由式(1-13)求合力在直角坐标轴上的投影;(2)由式(1-14)求合力的大小;(3)由式(1-15)求合力的方向。
答案:F R =161.2N , ∠(F R,F i)=29.701-3试计算下列各图中的力F对点O之矩。
解题思路:各小题均由式(1-16)求力矩。
答案:略1-4如图所示的挡土墙重G 1=75 kN ,铅直土压力G 2=120 kN ,水平土压力F p =90 kN 。
试求三力对前趾A 点之矩的和,并判断挡土墙是否会倾倒。
解题思路:(1)由式(1-16)求三力对前趾A 点之矩的代数和; (2)若其值为负(顺时针转),则挡土墙不会翻倒。
答案:∑M A =-180kN.m ,不会倾倒。
1-5如图所示,边长为a 的正六面体上沿对角线AH 作用一力F 。
试求力F 在三个坐标轴上的投影,力F 对三个坐标轴之矩以及对点O 之矩矢。
解题思路:(1)由式(1-13)、(1-14)、(1-15)求合力的大小和方向; (2)由式(1-25)求力对三个坐标轴之矩; (3)由式(1-26)求力对坐标原点之矩。
答案:M x =0,Fa M y 33=,Fa M 33z =-, k Fa j Fa M O 3333-=1-7试画出下列各图中物体A ,构件AB 的受力图。
未画重力的物体重量不计,所有接触面均为光滑接触。
解题思路:(1)画出研究对象的轮廓形状; (2)画出已知的主动力;(3)在解除约束处按约束的性质画出约束力。


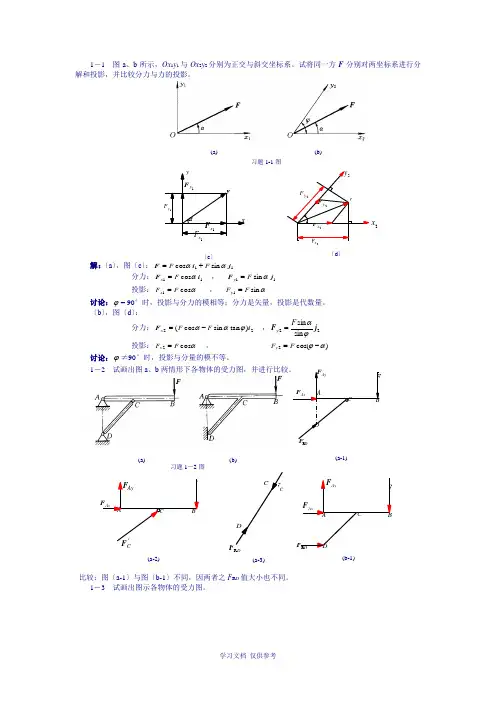
AyF FBCAAxF 'F CCDCF FAxF DR F FACBDAyFFDR F A CBD Ax F Ay F(a-1)第1篇 工程静力学基础第1章 受力分析概述1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1图解:(a )图(c ):11 sin cos j i F ααF F +=分力:11 cos i F αF x = , 11 sin j F αF y =投影:αcos 1F F x = , αsin 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b )图(d ): 分力:22)cot sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y = 投影:αcos 2F F x = , )cos(2αϕ-=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 和b 两种情形下各物体的受力图,并进行比较。
习题1-2图1y F x1F 1yF α1x F yF (c ) 2x F 2y F 2y 2x 2x F 2y F F(d )比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
1-3 试画出图示各物体的受力图。
习题1-3图F AxF AyF D C B A B F或(a-2)FF AF DCA(a-1)BF AxF AAyF C(b-1)W F BD C AyF F(c-1)F F CB B F A或(b-2) αDAF ABCBFAx F AAyFDF DC αF1-4 图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图C F CAAF (e-1) BF FCDBOOx F OyF W1O F A(f-1)FF DCABBF(e-3)'F AOOxF OyF AW(f-2)AF 1F A1O(f-3)F AF BF AAF xB 2F'yB 2F'1(c-1)F A B1B F(b-1)Dy F DDx F yB F C2(b-2)xB 2F'1F 1F'yB 2F'B(b-3)B WDxF DCyB F'(c-2)AF A D GF CH F H (a)1-5 图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
工程力学第2版课后习题答案_范钦珊主编_第1章_静力学基础
1.静力学研究的对象是()
A、物体
B、流体
C、物质
D、刚体
2.两个大小为3N、4N的力合成一个力时,此合力最大值为()
A、5N
B、7N
C、12N
D、1N
3.在研究拉伸与压缩应力应变时,我们把杆件单位长度的绝对变形称为()
A、应力
B、线应变
C、变形
D、正应力
4.质点动力学基本方程为(D)
A、W=FS
B、P=MV
C、I=FT
D、F=ma
5.以下关于截面上内力的大小的结论哪一个是正确的?()
A、与截面的尺寸和形状无关
B、与截面的尺寸有关,但与截面的形状无关
C、与截面的尺寸和形状有关
D、与截面的形状有关,但与截面的尺寸无关
6.当作用在质点系上外力系的主矢在某坐标轴上的投影为零时,则质点系质心的()
A.速度一定为零
B.速度在该轴上的投影保持不变
C.加速度在该轴上的投影一定不为零
D.加速度在该轴上的投影保持不变
7.一空间力系中各力的作用线均平行于某一固定平面,而且该力系又为平衡力系,则可列独立平衡方程的个数是()
A.6个
B.5个
C.4个
D.3个
8.已知点的运动方程为x=2t3+4,y=3t3-3,则其轨迹方程为()
A.3x+4y-36=0
B.3x-2y-18=0
C.2x-2y-24=0
D.2x-4y-36=0。
第一章静力学的基本概念受力图第二章 平面汇交力系2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 223R RX RY F F F KN=+= 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解:(a )受力分析如图所示:由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以:5RA F KN= (压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得: 22RA F Q =2RB F Q P=+(3)取BCE 部分。
(a) (b) 习题1-1图 (a) (b) 习题1-2图FD R F AC BD Ax F AyF(a-1) Ay F F B C A AxF 'F C (a-2)C D C F D R(a-3)AxF D R F FA C BD Ay F(b-1) 1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2别离为正交与斜交坐标系。
试将同一方F 别离对两坐标系进行分解和投影,并比较分力与力的投影。
解:(a ),图(c ):11 sin cos j i F ααF F += 分力:11 cos i F αF x = , 11 sin j F αF y = 投影:αcos 1F F x = , αsin 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b ),图(d ):分力:22)tan sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y =投影:αcos 2F F x = , )cos(2αϕ-=F F y 讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 、b 两情形下各物体的受力图,并进行比较。
比较:图(a-1)与图(b-1)不同,因二者之F R D 值大小也不同。
1-3 试画出图示各物体的受力图。
1y F x 1x F 1y F α1x F y F (c )2F 2y F 2y 2x 2x F 2y F F (d )习题1-3图1-4 图a 所示为三角架结构。
力F 1作用在B 铰上。
杆AB 不计自重,杆BD 杆自重为W 。
试画出图b 、c 、d 所示的隔离体的受力图,并加以讨论。
F AxF AyF D C B A B F 或(a-2) F B B AF D C A (a-1) B F AxF A Ay F B C(b-1)W F B DC Ay F AxF (c-1) F A F C BBF A或(b-2) αD A F A B CB FC F C AA F (e-1) Ax F A Ay F D F D C αF或(d-2)B F FCD B OOx F OyF W 1O F A(f-1)FA F D C AB B F (e-3) F AO Ox F OyF AW (f-2) A F 1O F A 1O (f-3) c F F A F D F B F A F AAx F C 'Cx F 'B F B AyF 'F Cy A(b-3)E F D F E D (a-3) CF F CE 'F E(a-2) 习题1-5图E EF B B F (b-2)CxF C CyF W T(b-1) Ay F Ax F 'BF 'C F C 'DF A D ED F EF 'E F E BB F CF C D(c) A F A D G FC HF H(a)B F BC 'C F D'D F Ax F Ay F A (a-1)1-5 试画出图示结构中各杆的受力图。