平均值代表值计算公式

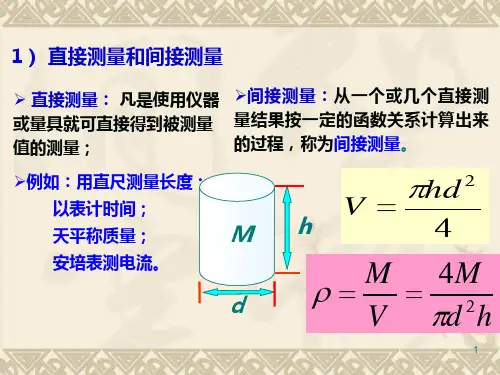
加权平均统计学名词．“统计初步”这部分内容中，平均数是一个非常重要而又有广泛用途的概念，在日常生活中，我们经常会听到这样一些名词：平均气温、平均降雨量、平均产量、人均年收入等；而平均分数、平均年龄、平均身高等名词更为同学们所熟悉.一般来说，平均数反映了一组数据的一般水平，利用平均数，可以从横向和纵向两个方面对事物进行分析比较，从而得出结论.例如，要想比较同一年级的两个班同学学习成绩，如果用每个班的总成绩进行比较，会由于班级人数不同，而使比较失去真正意义.但是如果用平均分数去比较，就可以把各班的平均水平呈现出来.从纵向的角度来看，可以对同一个事物在不同的时间内的情况利用平均数反映出来，例如，通过两个不同时间人均年收入来比较人们生活水平、经济发展等状况.但是，当一组数据中的某些数重复出现几次时，那么它们的平均数的表示形式发生了一定的变化.例如，某人射击十次，其中二次射中10环，三次射中8环，四次射中7环，一次射中9环，那么他平均射中的环数为:（10 *2+8*3+7*4+9*1）/10 = 8.1这里，7，8，9，10这四个数是射击者射中的几个不同环数，但它们出现的频数不同，分别为4，3，l，2，数据的频数越大，表明它对整组数据的平均数影响越大，实际上，频数起着权衡数据的作用，称之为权数或权重，上面的平均数称为加权平均数，不难看出，各个数据的权重之和恰为10.在加权平均数中，除了一组数据中某一个数的频数称为权重外，权重还有更广泛的含义.在评估某个同学一学期的学生成绩时，一般不只看他期末的一次成绩，而是将平时测验、期中考试等成绩综合起来考虑，比如说，一同学两次单元测验的成绩分别为88，90，期中的考试成绩为92，而期末的考试成绩为85，如果简单地计算这四个成绩的平均数，即将平时测验与期中、期末考试成绩同等看待，就忽视了期末考试的重要性.鉴于这种考虑，我们往往将这四个成绩分配以不同的权重。

由于10％＋10％＋30％＋50％=1，即各个权重之和为1，所以求加权平均数的式子中分母为1．下面的例子是未知权重的情况：股票A，1000股，价格10；股票B，2000股，价格15；算数平均 = (10 + 15) / 2 = 12.5；加权平均 = (10 x 1000 + 15 x 2000) / (1000 + 2000) = 13.33其实，在每一个数的权数相同的情况下，加权平均值就等于算数平均值。

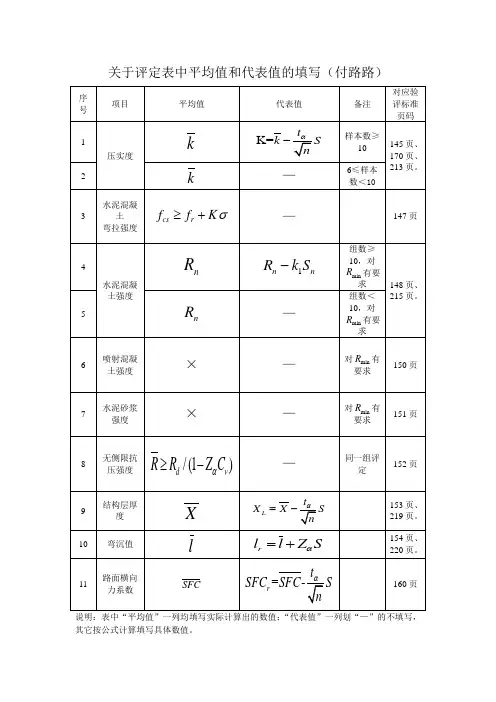
附录B 检测路段数据统计方法1 适用范围本方法规定了计算一个测试路段内测试结果的平均值、标准差、变异系数、实测值与设计值的差及代表值的方法。

本方法适应于本规程所列试验的数据统计工作，其他试验数据统计可参考使用。

2 计算2.1 按式（B-1）计算实测值X i 与设计值X 0之差。

ΔX i =X i -X 0 （B-1）式中：ΔX i ——实测值X i 与设计值X 0之差；X i ——第i 个测点的测试值；X 0——设计值。

2.2 测试结果的平均值、标准差、变异系数按式（B-2）～式（B-4）计算。

⎺X =NXi∑ （B-2） S∑（B-3）Cv = XS×100 （B-4）式中：X i ──第i 个测点的实测值； N ──一个测试路段内的测点数； X──一个测试路段内实测值的平均值； S ──一个测试路段内实测值的标准差；Cv ──一个测试路段内实测值的变异系数（%）。

2.3 计算一个测试路段内实测值的代表值时，对单侧测试的指标，按式（B-5）计算；对双侧测试的指标，按式（B-6）计算。

X ＇=⎺X ±SNt α （B-5）X ＇=⎺X ±SNt 2/α （B-6）式中：X ＇——一个测试路段内实测值的代表值；ｔα或t α/2——t 分布表中随自由度（N-1）和置信水平α（保证率）而变化的系数，见表B 。

保证率的选用还应符合相关规范的要求。

3 报告3.1 根据工程需要及现行相关规范规定，列出一个测试路段内实测值的记录表，记录平均值、标准差、变异系数及代表值。

注明不符合规范要求的测点。

3.2 当无特殊规定时，可疑数据的舍弃宜按照k 倍标准差作为舍弃标准，即在 资料分析中，舍弃那些在⎺X ±kS 范围以外的实测值，然后再重新计算整理。

当试验数据N 为3、4、5、6个时，k 值分别为1.15、1.46、1.67、1.82，N 等于或大于7时，k 值宜采用3。

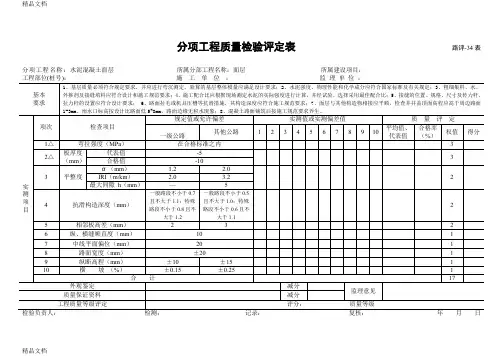
分项工程质量检验评定表路评-34表分项工程名称：水泥混凝土面层所属分部工程名称：面层所属建设项目：分项工程质量检验评定表路评-35表分项工程名称：沥青混凝土面层和沥青碎(砾)石面层所属分部工程名称：面层所属建设项目：分项工程质量检验评定表路评-36表分项工程名称：沥青贯入式面层（或上拌下贯式面层）所属分部工程名称：面层所属建设项目：检验负责人：检测：记录：复核：年月日分项工程质量检验评定表路评-37表分项工程名称：沥青表面处治面层所属分部工程名称：面层所属建设项目：检验负责人：检测：记录：复核：年月日分项工程质量检验评定表路评-38表分项工程名称：水泥土基层和底基层所属分部工程名称：面层所属建设项目：检验负责人：检测：记录：复核：年月日分项工程质量检验评定表路评-39表分项工程名称：水泥稳定粒料基层和底基层所属分部工程名称：面层所属建设项目：检验负责人：检测：记录：复核：年月日分项工程质量检验评定表路评-40表分项工程名称：石灰土基层和底基层所属分部工程名称：面层所属建设项目：检验负责人：检测：记录：复核：年月日分项工程质量检验评定表路评-41表分项工程名称：石灰稳定粒料基层和底基层所属分部工程名称：路面所属建设项目：检验负责人：检测：记录：复核：年月日分项工程质量检验评定表路评-42表分项工程名称：石灰、粉煤灰土基层和底基层所属分部工程名称：路面所属建设项目：检验负责人：检测：记录：复核：年月日分项工程质量检验评定表路评-43表分项工程名称：石灰、粉煤灰稳定粒料基层和底基层所属分部工程名称：面层所属建设项目：检验负责人：检测：记录：复核：年月日分项工程质量检验评定表路评-44表分项工程名称：级配碎（砾）石基层和底基层所属分部工程名称：面层所属建设项目：检验负责人：检测：记录：复核：年月日分项工程质量检验评定表路评-45表分项工程名称：填隙碎石（矿渣）基层和底基层所属分部工程名称：面层所属建设项目：检验负责人：检测：记录：复核：年月日分项工程质量检验评定表路评-46表分项工程名称：路缘石铺设所属分部工程名称：面层所属建设项目：检验负责人：检测：记录：复核：年月日分项工程质量检验评定表路评-47表分项工程名称：路肩所属分部工程名称：面层所属建设项目：检验负责人：检测：记录：复核：年月日。

加权平均统计学名词．“统计初步”这部分内容中，平均数是一个非常重要而又有广泛用途的概念，在日常生活中，我们经常会听到这样一些名词：平均气温、平均降雨量、平均产量、人均年收入等；而平均分数、平均年龄、平均身高等名词更为同学们所熟悉.一般来说，平均数反映了一组数据的一般水平，利用平均数，可以从横向和纵向两个方面对事物进行分析比较，从而得出结论.例如，要想比较同一年级的两个班同学学习成绩，如果用每个班的总成绩进行比较，会由于班级人数不同，而使比较失去真正意义.但是如果用平均分数去比较，就可以把各班的平均水平呈现出来.从纵向的角度来看，可以对同一个事物在不同的时间内的情况利用平均数反映出来，例如，通过两个不同时间人均年收入来比较人们生活水平、经济发展等状况.但是，当一组数据中的某些数重复出现几次时，那么它们的平均数的表示形式发生了一定的变化.例如，某人射击十次，其中二次射中10环，三次射中8环，四次射中7环，一次射中9环，那么他平均射中的环数为:（10 *2+8*3+7*4+9*1）/10 = 8.1这里，7，8，9，10这四个数是射击者射中的几个不同环数，但它们出现的频数不同，分别为4，3，l，2，数据的频数越大，表明它对整组数据的平均数影响越大，实际上，频数起着权衡数据的作用，称之为权数或权重，上面的平均数称为加权平均数，不难看出，各个数据的权重之和恰为10.在加权平均数中，除了一组数据中某一个数的频数称为权重外，权重还有更广泛的含义.在评估某个同学一学期的学生成绩时，一般不只看他期末的一次成绩，而是将平时测验、期中考试等成绩综合起来考虑，比如说，一同学两次单元测验的成绩分别为88，90，期中的考试成绩为92，而期末的考试成绩为85，如果简单地计算这四个成绩的平均数，即将平时测验与期中、期末考试成绩同等看待，就忽视了期末考试的重要性.鉴于这种考虑，我们往往将这四个成绩分配以不同的权重。

由于10％＋10％＋30％＋50％=1，即各个权重之和为1，所以求加权平均数的式子中分母为1．下面的例子是未知权重的情况：股票A，1000股，价格10；股票B，2000股，价格15；算数平均 = (10 + 15) / 2 = 12.5；加权平均 = (10 x 1000 + 15 x 2000) / (1000 + 2000) = 13.33其实，在每一个数的权数相同的情况下，加权平均值就等于算数平均值。

弯沉自动计算表(含弯沉计算及标准差、代表值、平均值)本文档旨在介绍弯沉自动计算表的目的和作用，并概括说明将要涵盖的内容。

弯沉自动计算表是一种工具，用于计算建筑结构弯曲所引起的沉降，并分析数据以获得标准差、代表值以及平均值。

通过使用这个自动计算表，工程师可以快速而准确地评估结构的稳定性和安全性，从而有效地进行设计和施工。

本文档将按照以下大纲进行详细阐述：弯沉计算的基本原理和公式弯沉自动计算表的使用方法和步骤弯沉计算表的示例和案例分析弯沉计算表的优势和局限性结论和建议通过阅读本文档，您将了解如何使用弯沉自动计算表来进行弯沉计算，分析数据，并获得标准差、代表值以及平均值。

这将为工程师提供一个有力的工具，以确保建筑结构的稳定性和安全性。

请继续阅读以下章节以获得更详细的信息。

弯沉计算表是用于计算土地或建筑物的弯沉的工具。

它能帮助确定土地或建筑物的变形情况，以便进行结构设计或维护工作。

以下是如何使用弯沉自动计算表进行弯沉计算的步骤：输入数据：将土地或建筑物的测量数据输入到弯沉自动计算表中。

这些数据通常包括测量点的坐标、观测时间、观测值等。

计算公式：弯沉自动计算表使用特定的公式来计算弯沉值。

这些公式可以根据土地或建筑物的特性进行调整。

步骤：根据弯沉自动计算表的指导，按照指定的步骤进行计算。

这些步骤包括数据处理、公式应用和结果计算等。

弯沉自动计算表可以简化弯沉计算的过程，提高计算的准确性和效率。

通过使用弯沉自动计算表，土地测量人员或工程师可以更方便地进行弯沉计算，并及时获取准确的结果。

标准差：标准差是一种统计指标，用于衡量数据的离散程度。

在弯沉计算中，标准差可以帮助我们了解测量值的变化范围。

较大的标准差表示数据的离散程度较高，而较小的标准差则表示数据的离散程度较低。

标准差：标准差是一种统计指标，用于衡量数据的离散程度。

在弯沉计算中，标准差可以帮助我们了解测量值的变化范围。

较大的标准差表示数据的离散程度较高，而较小的标准差则表示数据的离散程度较低。