当前位置：文档之家 › 新人教版22.1.2-二次函数y=ax2的图象和性质

新人教版22.1.2-二次函数y=ax2的图象和性质

  • 格式：ppt
  • 大小：1.78 MB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

22.1.2二次函数y=ax2的图象和性质

22.1.2二次函数y=ax2的图象和性质


知识点三
画二次函数的图象,列表时取的点越多,图象往往越准确,但是 一般采用“五点法”或“七点法”画图,画图时应注意: (1)描点法所画的图象只是整个函数图象的一部分,是近似的, 由于x可取一切实数,所以图象是向两方无限延伸的; (2)点取得越多,图象画得越精确,在限定条件下(即限定自变量 的取值范围)或在实际问题中,函数的图象必须要根据自变量 的取值范围取其中的一部分; (3)所画图象必须平滑(符合点的发展变化的趋势),尤其是顶点 不能画成“尖”形的.
22.1.2
二次函数y=ax2的图象和性质
知识点一
知识点二
知识点三
知识点一二次函数y=x2的图象和性质 二次函数y=ax2+bx+c的图象是抛物线,对称轴与抛物线的交点叫 做顶点,顶点是抛物线的最低点或最高点. 对于特殊的二次函数y=x2,对称轴是y轴,顶点是(0,0),顶点是它的 最低点,在对称轴的左侧,抛物线从左到右下降;在对称轴的右侧,抛 物线从左到右上升.也就是说,当x<0时,y随x的增大而减小;当x>0 时,y随x的增大而增大. 名师解读:理解和记忆二次函数的性质时,可以从y=x2得到启发, 其他二次函数的图象及性质可类比y=x2的图象和性质,主要从开口 方向、对称轴、顶点、增减性等几个方面去进行.
知识点一
知识点二
知识点三
知识点二y=ax2的图象 一般地,抛物线y=ax2的对称轴是y轴,顶点是原点.当a>0时,抛物线 的开口向上,顶点是抛物线的最低点;当a<0时,抛物线的开口向下, 顶点是抛物线的最高点.对于y=ax2,|a|越大,抛物线的开口越小. 名师解读:二次函数y=ax2的图象是抛物线,结合图象可知,二次项 系数a的符号决定了开口方向,|a|决定了开口的大小.
人教版九年级上册数学22.1.2 二次函数的图象和性质

人教版九年级上册数学22.1.2 二次函数的图象和性质

22.1.2 二次函数y＝ax2的图象和性质
一、教学目标
1．会用描点法画二次函数y＝ax2的图象，理解抛物线 的有关概念． 2．掌握二次函数y＝ax2的性质，能确定二次函数y＝ ax2的解析式． 3．经历从特殊到一般的认识过程，学会合情推理．
二、教学重难点
重点 1．二次函数y＝ax2的图象的画法及性质． 2．能确定二次函数y＝ax2的解析式．
难点 1．用描点法画二次函数y＝ax2的图象，探索其性质． 2．能运用二次函数y＝ax2的有关性质解决问题．
三、教学设计
活动1 新课导入 1．一次函数y＝kx＋b(k≠0)的图象是_一__条__经__过__(_0_，__b_)的__ 直__线__．特别地，正比例函数y＝kx(k≠0)的图象是 过__原__点__的__直__线__． 2．描点法画出一次函数的步骤：分别为_列__表_、_描__点_、 _连__线_三个步骤． 3．我们把形如_y_＝__a_x_2_＋__b_x_＋__c_(a_≠_0_)_的函数叫做二次函 数．
(3)你能总结归纳出当a＜0时，y＝ax2的图象和性质吗 ？ 一般地，当a ＜ 0时，抛物线 y＝ax2 的开口向下，对 称轴是 y 轴，顶点是原点，顶点是抛物线的最高点，a 越小，抛物线的开口越小
活动3 知识归纳
1．二次函数y＝ax2的图象是一条开口向上或向下的抛 物线．一般地，二次函数y＝ax2＋bx＋c的图象叫做抛 物线y＝ax2＋bx＋c.
活动4 例题与练习
例1 已知函数y＝(m＋2)xm2＋2m－6是关于x的二次函数. (1)求m的值； (2)当m为何值时，此函数图象的顶点为最低点？ (3)当m为何值时，此函数图象的顶点为最高点？ 解：(1) m＋2≠0，m2＋2m－6＝2，解得m1＝2，m2＝－ 4，∴ m的值为2或－4； (2)若函数图象有最低点，则抛物线的开口向上，∴ m ＋2＞0，解得 m＞－2，∴ m＝2； (3)若函数图象有最高点，则抛物线的开口向下，∴ m ＋2＜0，解得 m＜－2，∴ m＝－4.
人教版九年级上册数学 22.1.2 二次函数 y=ax2的图象和性质课件

人教版九年级上册数学 22.1.2 二次函数 y=ax2的图象和性质课件


a<0
1 -5-4-3-2-1 -1o1 2 3 4 5 x -2 -3 -4 -5 -6 -7 -8 -9 1 -10 y x2
y
2
y 2 x 2
y x2
总结性质
1.形如二次函数 y=ax2 的图象都是顶点为
（ 0 ， 0） ______ 的抛物线，反之，顶点在（0,0）
2 y = ax 的抛物线的形式是_________.
体验画图
抛物线的定义：
实际上,二次函数的图象是抛物线，
它们开口向上或向下，一般地，二次
函数 y ax bx c 的图象叫做抛
2 2
物线 y ax bx c .
体验画图
3. 拓展与延伸： 3 个点， （1）画二次函数的图象一般需要___
哪些点比较关键？ 抛物线
yx
2
轴 对称图形，对称 是__
y 10 9 8 7 6 5 4 3 2 1 -5-4-3-2-1 O1 2 3 4 5 x
a>0
体验画图
（3）以上都是当a >0时，二次函数 y ax 的图象，
2
那么当 a<0时，试在同一直角坐标系画出二次函数：
1 2 y x ，y x ，y 2 x 2 的图象. 2
2
关于 y 轴对称 原点（0，0）
对称性
顶点
总结提高
2. 二次项系数 a 对形如 y=ax2 的函数值 y 又有
何影响？对图象又有何影响？
y＝ax2
开口
a>0 开口向上
a<0 开口向下
增减性 在对称轴左侧递减 在对称轴左侧递增 在对称轴右侧递增 在对称轴右侧递减
LOGO
人教版九年级数学上册22.1.2《二次函数y=ax2的图象和性质》教案

人教版九年级数学上册22.1.2《二次函数y=ax2的图象和性质》教案

人教版九年级数学上册22.1.2《二次函数y=ax2的图象和性质》教案一. 教材分析人教版九年级数学上册第22.1.2节《二次函数y=ax^2的图象和性质》是九年级数学的重要内容，主要让学生了解二次函数的图象特征和性质。

通过本节课的学习，学生能理解二次函数的一般形式，掌握二次函数的图象特征，了解二次函数的增减性和对称性，从而为后续的函数学习打下基础。

二. 学情分析学生在学习本节课之前，已经掌握了函数的基本概念，具备了一定的函数知识。

但对于二次函数的图象和性质，可能还存在一定的困惑。

因此，在教学过程中，教师需要关注学生的学习情况，针对学生的实际问题进行讲解，引导学生理解和掌握二次函数的图象和性质。

三. 教学目标1.让学生理解二次函数的一般形式，掌握二次函数的图象特征。

2.让学生了解二次函数的增减性和对称性，能运用二次函数的性质解决实际问题。

3.培养学生的观察能力、分析能力和解决问题的能力。

四. 教学重难点1.二次函数的一般形式和图象特征。

2.二次函数的增减性和对称性。

五. 教学方法1.采用问题驱动法，引导学生主动探究二次函数的图象和性质。

2.利用多媒体辅助教学，直观展示二次函数的图象，帮助学生理解。

3.采用小组合作学习，培养学生的团队协作能力。

六. 教学准备1.多媒体教学设备。

2.二次函数图象和性质的相关教学素材。

3.学生分组合作学习的材料。

七. 教学过程导入（5分钟）教师通过提问方式引导学生回顾一次函数和正比例函数的图象和性质，为新课的学习做好铺垫。

同时，教师可以利用多媒体展示二次函数的图象，让学生初步感受二次函数的特点。

呈现（10分钟）教师给出二次函数的一般形式y=ax^2，让学生观察并分析二次函数的图象特征。

学生通过观察多媒体展示的二次函数图象，总结出二次函数的开口方向、顶点坐标等特征。

操练（10分钟）教师给出几个二次函数的实例，让学生分析其图象特征。

学生通过小组合作学习，探讨并分析二次函数的增减性和对称性。

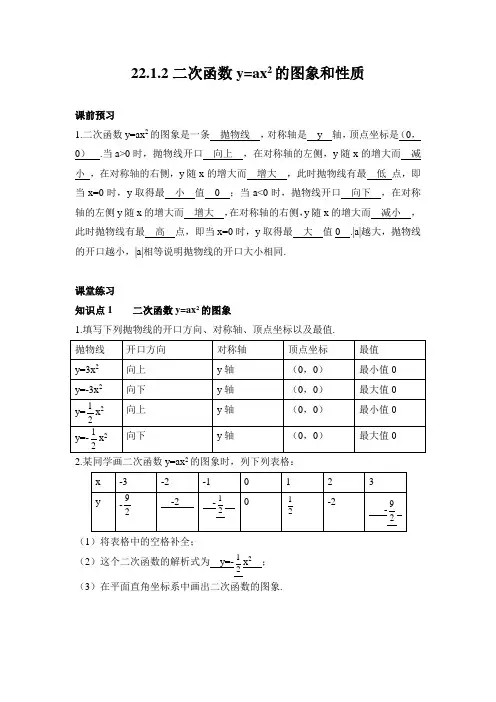
22.1.2二次函数y=ax2的图象和性质 参考解析

22.1.2二次函数y=ax2的图象和性质 参考解析

22.1.2二次函数y=ax2的图象和性质课前预习1.二次函数y=ax2的图象是一条抛物线，对称轴是y 轴，顶点坐标是（0，0）.当a>0时，抛物线开口向上，在对称轴的左侧，y随x的增大而减小，在对称轴的右侧，y随x的增大而增大，此时抛物线有最低点，即当x=0时，y取得最小值0 ；当a<0时，抛物线开口向下，在对称轴的左侧y随x的增大而增大，在对称轴的右侧，y随x的增大而减小，此时抛物线有最高点，即当x=0时，y取得最大值0 .|a|越大，抛物线的开口越小，|a|相等说明抛物线的开口大小相同.课堂练习知识点1 二次函数y=ax2的图象1.填写下列抛物线的开口方向、对称轴、顶点坐标以及最值.2.某同学画二次函数y=ax2的图象时，列下列表格：（1）将表格中的空格补全；（2）这个二次函数的解析式为y=-1x2；2（3）在平面直角坐标系中画出二次函数的图象.解：（3）函数图象如图所示.知识点2 二次函数y=ax2的性质3.已知二次函数y=（m-2）x2的图象开口向上，则m的取值范围是m>2 .4.下列各点在二次函数y=-2x2图象上的是（ B ）A.（-1，2）B.（-1，-2）C.（-2，-4）D.（-2，4）5.关于函数y=x2的图象，下列说法错误的是（ C ）A.它的图象是一条抛物线B.它的开口向上，且关于y轴对称C.它的顶点是抛物线的最高点D.它的顶点在原点处，坐标为（0，0）课时作业1.与二次函数y=x2开口大小相同，方向相反的二次函数是y=-x2.2.二次函数y=-0.2x2的图象是一条开口向下的抛物线，对称轴是y轴，顶点坐标为（0，0）.当x= 0 时，函数有最大值0 ；当x ＞0时，y随x的增大而减小.3.关于函数y=3x2的性质，下列说法正确的是（ C ）A.无论x为任何实数，y的值总为正B.当x值增大时，y的值也增大C.它的图象关于y轴对称D.它的图象在第一、第三象限内4.已知A （-1，y ₁），B （-2，y ₂）都在二次函数y=x 2上，则y ₁，y ₂之间的大小关系是（ C ）A.y ₁>y ₂B.y ₁=y ₂C.y ₁<y ₂D.不能确定 5.二次函数y=ax 2（a ＞0）的图象经过点（3，4），则其图象一定经过点（ C ） A.（3，-4） B.（-3，-4） C.（-3，4） D.（4，3）6.如图，当ab ＞0时，函数y=ax 2与函数y=bx+a 的大致图象是（ C ）7.二次函数y=2x 2，y=-2x 2，y=12x 2的共同性质是（ B ） A.开口向上 B.对称轴是y 轴 C.都有最高点 D.y 随x 的增大而增大 8.已知函数y=（m+2）226m m x +-是关于x 的二次函数. （1）求m 的值；（2）当m 为何值时，函数图象的顶点为最低点？ （3）当m 为何值时，函数图象的顶点为最高点？ 解：（1）根据二次函数的定义得22026 2.m m m +≠+-=⎧⎨⎩，解得⎩⎨⎧-==.4,221m m ∴m 的值为2或-4；（2）当m=2时，抛物线的开口向上，函数有最小值，函数图象的顶点为最低点； （3）当m=-4时，抛物线的开口向下，函数有最大值，函数图象的顶点为最高点.9.在同一个平面直角坐标系中，画出下列函数的图象：①y=x 2；②y=12x 2；③y=-x 2；④y=-12x 2.从图象上对比，说出解析式中二次项系数a对抛物线的形状有什么影响？解：列表如下描点、连线，函数图象如图所示a的绝对值相同，抛物线的形状相同；a的绝对值越大，开口越小.10.如图，A，B为抛物线y=x2上的两点，且AB∥x轴，与y轴交于点C，以点O为圆心，OC为半径画圆，若2.解：∵AB=22∴BC=122∴点B的横坐标为2代入抛物线的解析式得y=2.∵AB∥x轴，∴点B与点C的纵坐标相同.∴OC=2，即圆的半径为2.由二次函数的对称性得，图中阴影部分的面积等于圆面积的14， 即S 阴影=14π×22=π.11.函数y=ax 2（a ≠0）的图象与直线y=2x-3交于点（1，b ）. （1）求a 和b 的值；（2）x 在什么范围时，二次函数y=ax 2中的y 随x 的增大而增大？ （3）求抛物线y=ax 2与直线y=-2的两个交点及顶点所围成的三角形的面积. 解：（1）把点（1，b ）代入y=2x-3，得b=-1. ∴交点坐标为（1，-1）. 把（1，-1）代入y=ax 2，得a=-1. ∴a=-1，b=-1；（2）由（1）得y=-x 2，当x ≤0时，y 随x 的增大而增大； （3）根据题意，得2,2.y x y ⎧=-⎨=-⎩解得2x y ⎧=⎪⎨=-⎪⎩或 2.x y ⎧=⎪⎨=-⎪⎩ ∴两交点坐标分别为（-2），（-2）.故S △=12×。

22.1.2 二次函数y=ax2的图象和性质

22.1.2 二次函数y=ax2的图象和性质


2.下列关于二次函数y=ax²（a≠0）的说法中，错 误的是（ C ） A.它的图像的顶点是原点 B.当a＜0，在x=0时，y取得最大值 C.a越大，图像开口越小；a越小，图像开口越大 D.当a＞0，在x＞0时，y随x的增大而增大
3.请在同一坐标系中画出函数y1=x和y2=-x²的图 像，结合图像，指出当x取何值时，y1＞y2；当x 取何值时，y1＜y2。 列表如下：
a值越大，
开口越大， a值越小， 开口越小
y轴
(0,0)
1.二次函数y=ax2的图像是一条向上或向下的 抛物线。
2.二次函数y=小，开口越大。 |a|值相同，开口形状相同。
随堂演练
1.若抛物线y=ax²与y=4x²的形状及开口方向 均相同，则a= 4
不同点？
（2）当a＜0时，二次函数
y=ax² 的图象有什么特点？
二次函数y=ax²的图像及其性质
抛物线 a的 开口方向 符号 与大小
开口向上 a值越大， a>0 开口越小， a值越小， 开口越大 开口向上 a<0 y轴 (0,0)
对称轴
顶点 最大（小） 增减性 坐标 值
在对称轴左侧， 当X=0时 y随x增大而减 小;在对称轴 y有最小 右侧， 值， y随x 增大而 y最小=0 增大 在对称轴左侧， 当X=0时 y随x增大而增 大;在对称轴 y有最大 右侧， 值， y随x 增大而 y最大=0 减小
（3）根据图像指出，当x＞0时，若x增大，y怎么变化？ 当x＜0时，若x增大，y怎样变化？
（4）当x取何值时，y有最大（或最小）值，其值为多少？
（1）求这个二次函数的解析式 解：设这个二次函数解析式为 y =ax2，将（-1，）代入得y=
1 4
22.1.2二次函数y=ax2图像与性质

22.1.2二次函数y=ax2图像与性质


y=ax2+c (a≠0) 开口方向 顶点坐标 对称轴 增 减 性 极值
a>0 向上 (0 ,c) y轴
当x<0时， y随着x的增大而减小。 当x>0时， y随着x的增大而增大。
a<0 向下 (0 ,c) y轴
当x<0时, y随着x的增大而增大。 当x>0时， y随着x的增大而减小。
x=0时,y最小=c
x y = x2 · · · · · · －3 －2 －1 0 1 2 3 · · · · · ·
9
4
1
0
1
9
4
9
2. 根据表中x,y的数值在 坐标平面中描点（x,y） 3.连线 如图，再用平 滑曲线顺次连接各点， －3 2 就得到y = x 的图象．
y = x2
6
3 3
二次函数 y = x2的图象是一条曲线，它的形状类似 于投篮球时球在空中所经过的路线，只是这条曲线 开口向上，这条曲线叫做抛物线 y = x2 ， 二次函数的图象都是抛物线， 它们的开口或者向 上或者向下． 一般地，二次函数 y = ax2 + bx + c （a≠0）的图象叫做抛物线y = ax2 + bx + c y = x2
m2+m
解②得:m1=－2, m2=1 由①得:m>－1 ∴ m=1 此时,二次函数为: y=2x2,
x ….. y=x2 …… y=x2+1 ……
-2 4
-1 1
0 0
y
8
1 1
2 4
…… ……
5
2
0
2
5

y=x2+1
函数y=x2+1的图象与y=x2的 图象的位置有什么关系? 函数y=x2+1的图 象与y=x2的图象 的形状相同吗?
人教版数学九年级上册22.1.2二次函数y=ax2的图像与性质 课件(21张PPT)

人教版数学九年级上册22.1.2二次函数y=ax2的图像与性质 课件(21张PPT)


二二次次函函数数y的=图x2象的都图是象抛是物一线条，曲线它，们它的的开形口状或类者似向于上投或篮者球向 时下球．在一空般中地所，经二过次的函路数线y，=只ax是2 +这b条x +曲c线（开a≠口0）向的上图，象这叫条做曲抛 线物叫线做y =抛a物x2线+ byx=+xc2 ，
9 6 3
－3
3
实y轴际是上抛，物每线条y抛= 物x 2线的都对有称对轴称，轴抛，物抛线物y 线= x与2 对与称它轴的的对交称点轴 叫的做交抛点物（线0，的0顶）点叫．做顶抛点物是线抛y =物x线2 的的顶最点低，点它或是最抛高物点线．y = x 2 的最低点．
交点坐标
y
求抛物线与直线的 交点坐标的方法： 两解析式联列方程
组
y=4x2 y=3x+1
O
x
1.若抛物线y=ax²与y=4x²的形状及开口方向 均相同，则a= 4
2.下列关于二次函数y=ax²（a≠0）的说法中，错误 的是（ C ） A.它的图像的顶点是原点 B.当a＜0，在x=0时，y取得最大值
(2)说出函数图象的顶点坐标、对称轴、
开口方向和图象的位置；
在x轴的下方
解: (1)依题意，得 (2)2 a 3
解得
a=

3 4
∴ 该函数的解析式为 y


3 4
x2
例3、y=kx2与y=kx－2(k≠ 0)在同一坐标系中， 可能是（ B ）
A
B
C
D
例4、求抛物线y=4x2与直线y=3x+1的
描点法
列表、描点、连线
以0为中心 选取7个x值
画最简单的二次函数 y = x2 的图象列表
22.1.2 二次函数y=ax2的图象和性质

22.1.2 二次函数y=ax2的图象和性质


x
… -2 -1
0
1
y=2x2 …
y=2x2
…
(2)描点并连线:
2
…
…
…
【思路点拨】 首先列表求出函数图象上点的坐标,进而描点连线画出图象即可.注 意连线时一定要用平滑的实线连接.
解:(1)8 2 0 2 8 -8 -2 0 -2 -8 (2)
类型二:二次函数y=ax2图象的性质的应用
例2 已知函数y=ax2的图象过点(1, 1 ).
2
增大而减小.
(2)在其图象上有两点(x1,y1),(x2,y2),且x1>x2>0,比较y1,y2的大小.
【思路点拨】 (2)二次函数y=ax2的对称轴为y轴,由(1)知a<0,所以在其对称轴 的右侧y随x的增大而减小,又x1>x2>0,故y1<y2. 解:(2)因为x1>x2>0, 所以y1<y2.

(1)简述函数y=ax2的性质;
2
【思路点拨】 (1)把点(1, 1 )代入函数y=ax2的解析式求得a的值,即可判定函
数的性质.
2
解:由题意得 a=- 1 ,所以 y=- 1 x2.
2
2
(1)函数 y=- 1 x2,开口向下,在 y 轴左侧 y 随 x 的增大而增大,在 y 轴右侧 y 随 x 的
22.1.2 二次函数y=ax2的图象和性质
1.二次函数y=ax2的图象
二次函数y=ax2的图象是 抛物线 ,对称轴与抛物线的交点叫做 顶点 ,顶点是
(0,0) ,当a>0时,抛物线的开口 向上 ,顶点是抛物线的最 低 点;当a<0时, 抛物线的开口 向下 ,顶点是抛物线的最 高 点.对于y=ax2,|a|越 大 ,抛物 线的开口越小.
22_1_2 二次函数y=ax2的图象和性质【人教九上数学学霸听课笔记】

22_1_2 二次函数y=ax2的图象和性质【人教九上数学学霸听课笔记】


探 归纳
究 与
3.如果a<0,
应 用
(1)抛物线的开口向____下____,顶点是抛物线的最x的增大而___增__大___,当x>0时,y随x的增大而
___减__小___.
4.对于抛物线y＝ax2,|a|越大,抛物线的开口越___小_____.
探 究
变式 说出下列抛物线的开口方向、对称轴和顶点.
第 二
二次函数
十 二
22.1 二次函数的图象和性质
章
-
22.1.2 二次函数y＝ax2的图象和性质
预学浅梳理 探究与应用 随堂小检测
预 根据二次函数y＝ax2的图象和性质,填写下表：
学
浅
函数
y＝ax2
梳
理
a的取值
a>0
a<0
图象
预
函数
学
浅 开口方向
梳
理 顶点坐标
对称轴
y＝ax2
向___上_____
最值 当x＝0时,y最小值＝ ____0____
当x＝0时,y最大值＝ ____0____
探 目标一 会用描点法画出二次函数y＝ax2的图象,了解抛
究
物线的有关概念
与
应 探究 (1)画图：请根据下面的步骤用描点法画出二次函数y
用 ＝x2的图象.
①列表：选取适当的x值,并计算相应的y值,完成下表：
x … －3 －2 －1 0 1 2 3 …
探 究
②在对称轴___左__侧___,抛物线y＝x2从左到右下降；在对称
与 轴右侧,抛物线从左到右__上__升____.也就是说,当x<0时,y随x的
应 用
增大而___减__小___；当x>0时,y随x的增大而___增__大___.
数学人教版九年级上册22.1.2二次函数y=ax2的图象与性质

数学人教版九年级上册22.1.2二次函数y=ax2的图象与性质


y=-x2
1. 二次函数的图像都是抛物线.
2. 抛物线y=ax2的图像性质: (1) 抛物线y=ax2的对称轴是y轴,顶点是原点. (2)当a>0时,抛物线的开口向上,顶点是 抛物线的最低点; 当a<0时,抛物线的开口向下,顶点是 抛物线的最高点; |a|越大,抛物线的开口越小 ;
y
a>0
o
x
a<0
跑的越快，遇到风的阻力越大。阻 力与成就相伴随。
没有斗狼的胆量，就不要牧羊。
望远镜---可以望见远的目标，却不 能代替你走半步。
只有脚踏实地的人，才能够说：路 ，就在我的脚下。
站在巨人的肩上是为了超过巨人。
成绩和劳动是成正比例的，有一分 劳动就有一分成绩。
你既然认准一条道路，何必去打听 要走多久。
抛物线 y= -x2在x轴下方(除顶点外)，顶点 是它的最高点，开口向下，并且向下无限伸展， 当x=0时，函数y的值最大，最大值是0.
y
y x
2
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
例1.画出函数y=x2、y=2x2、y= 2 x2的图象：
1
探究
顶点坐标
请同学们把所学的二次函数图象的知识归纳小结。
(0,0) 最低点 y轴 向上
增 减 增增 大 小 大大
(0,0) 最高点
y轴
向下
增 增 增减 大 大 大小
老师寄语：
• 老师能给你们的唯有这无形的知识，但老 师希望你们用这些无形的知识创造出有形 的世界，实现你们的中国梦，老师就是你 们的筑梦人！
一帆风顺，并不等于行驶的是一条 平坦的航线。
y=2x2
பைடு நூலகம்

人教版九年级数学上册22.1.2《二次函数y=ax2的图象和性质》教学设计

人教版九年级数学上册22.1.2《二次函数y=ax2的图象和性质》教学设计一. 教材分析人教版九年级数学上册22.1.2《二次函数y=ax2的图象和性质》这一节主要介绍了二次函数y=ax2的图象和性质。

内容包括：二次函数的图象是抛物线，讨论了抛物线的开口方向、对称轴、顶点坐标等，并学习了如何通过a的值来判断抛物线的性质。

这部分内容是整个初中数学的重要知识点，对于学生来说，理解和掌握二次函数的图象和性质对于后续学习其他数学知识有着重要的基础作用。

二. 学情分析九年级的学生已经学习了函数的基本概念和一次函数、二次函数的定义，对于函数有一定的认识和理解。

但在学习这一节内容时，学生可能对于抛物线的性质和开口方向的判断还存在一定的困难。

因此，在教学过程中，需要引导学生通过观察、操作、思考、探究等活动，加深对二次函数图象和性质的理解。

三. 教学目标1.理解二次函数y=ax^2的图象和性质，能够判断抛物线的开口方向、对称轴和顶点坐标。

2.培养学生观察、操作、思考、探究的能力，提高学生解决问题的能力。

3.培养学生的合作意识和团队精神，提高学生的沟通表达能力。

四. 教学重难点1.二次函数y=ax^2的图象和性质的理解和掌握。

2.抛物线开口方向、对称轴和顶点坐标的判断。

五. 教学方法1.采用问题驱动法，引导学生通过观察、操作、思考、探究等活动，自主发现和总结二次函数的图象和性质。

2.采用小组合作学习法，让学生在小组内进行讨论、交流、分享，提高学生的合作意识和团队精神。

3.采用案例分析法，通过具体的例子，让学生理解和掌握二次函数的图象和性质。

六. 教学准备1.PPT课件2.教学工具（黑板、粉笔等）七. 教学过程1.导入（5分钟）通过一个实际问题，引出二次函数y=ax^2的概念，激发学生的学习兴趣。

2.呈现（10分钟）利用PPT课件，展示二次函数y=ax^2的图象和性质，让学生直观地感受和理解。

3.操练（10分钟）让学生通过观察、操作、思考、探究等活动，自主发现和总结二次函数的图象和性质。

22.1.2二次函数y=ax2的图像和性质教案

1.注重个体差异，针对不同学生的理解程度，进行有针对性的讲解和指导。
2.增加课堂互动，鼓励学生提问和发表观点，提高他们的课堂参与度。
3.丰富教学手段，运用多媒体、实物演示等手段，让学生更直观地理解二次函数的性质。
4.加强课后辅导，关注学生对知识点的掌握情况，及时解答他们的疑问。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解二次函数y=ax2的基本概念。二次函数是形如y=ax2的函数，其中a为常数，且a≠0。它是描述物体抛物线运动、图形变换等方面的重要数学工具。
2.案例分析：接下来，我们来看一个具体的案例。这个案例展示了二次函数y=ax2在抛物线运动中的应用，以及它如何帮助我们解决问题。
3.掌握二次函数y=ax2的增减性，会判断给定区间内函数的增减情况；
4.掌握二次函数y=ax2的最大（小）值及其取值情况。
二、核心素养目标
（1）通过探究二次函数y=ax2的图像和性质，培养学生的直观想象和逻辑推理能力；
（2）使学生能够运用数学语言表达二次函数的性质，提高学生的数学表达能力；
（3）培养学生运用二次函数解决实际问题的能力，增强数学应用意识；
4.学生小组讨论环节，大家围绕二次函数在实际生活中的应用展开了热烈的讨论。但在分享成果时，我发现有些小组的成果过于表面，没有深入挖掘二次函数的性质。为此，我将在接下来的教学中，加强引导，让学生更好地运用所学知识解决实际问题。
结回顾环节，学生对本节课的知识点有了更深入的理解，但仍有个别学生对二次函数的增减性和最值掌握不够牢固。在今后的教学中，我会加强这些知识点的巩固。
（4）通过小组合作学习，培养学生的团队协作能力和交流沟通能力；
（5）引导学生发现二次函数图像与性质之间的关系，提高学生的数据分析能力。

22.1.2 二次函数y=ax2的图象和性质


(1) 列表 (2) 描点 (3) 连线
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=2x2 … 8 4.5 2 0.5 0 0.5 2 4.5 8 …
y = 2x2 y
10
9 8 7 6 5 4
3 2 1
y = x2 y = ▁21 x2
-5 -4 -3 -2 -1 0 1 2 3 4 5 x
二次函数 y = x2的图 象是轴对称图形， 对称轴是 y 轴
10 y
9 8
7 6 5 4 3 2 1
y = x2
-5 -4 -3 -2 -1 0 1 2 3 4 5 x
从左到右：上升 y随x：增大而增大
抛物线 y = x2与它的对称轴的 交点(0,0)叫做抛物线 y = x2的 顶点 它是抛物线 y = x2的最低点．
1
-3 -2 -1 0 1 2 3 x
(3) 连线
-1
y 1 x2
-2
2
-3
y x2
-4
-5 y 2 x2
22.1.2 二次函数 y=ax²的图象和性质
函数 y=- 1 x2（橘黄线）, y=-2x2（绿线）的图象与
2
函数 y=-x2(蓝线)的图象相比,有什么共同点和不同点?
y
相同点：开口：向下， 顶点：原点（0,0）——最高点
实际上, 二次函数的图象都是抛物线，
一般地，二次函数 y = ax2 + bx + c（a≠0） 的图象叫做抛物线 y = ax2 + bx + c
y 10
9
8 7
y = x2
6
5
4
3
2
1

22.1.2二次函数y=ax2 的图象和性质


8、函数y=ax2与y=－ax+b的图象可能是（
）
A．
B．
．
C．
D
9、已知函数y=(m+1)xm2-m-4是关于x的二次函数， 求：①、满足条件的m的值； ②m为何值时，抛物线有最低点？ 求出这个最低点，这时x为何值时， y随x的增大而增大； ③m为何值时，抛物线有最大值？ 最大值是多少？当x为何值时， y随x的增大而减小？
10、 已知抛物线y=ax2经过点A（-2，-8）. （1）求此抛物线的函数解析式； （2）判断点B（-1，- 4）是否在此抛物线上. （3）求出此抛物线上纵坐标为-6的点的坐标.
11、如果抛物线y=ax2与直线y=x+1交于点(m,2)， 求这条抛物线所数y=ax2的图象是什么？
2 2 （2）抛物线 y x 在x轴的 下 方（除顶点外），在对称轴的 3 左侧，y随着x的 增大而增大 ；在对称轴的右侧，y随着x的
增大而减小 ，当x=0时，函数y的值最大，最大值是 当x 0 ，

0时，y<0.
1、抛物线 y＝2x2 不具有的性质是（ ） A、开口向下 B、对称轴是 y 轴 C、与 y 轴不相交 D、最低点是原点
2 22.1.2二次函数y=ax
的图象和性质
1．复习研究函数的一般方法
问题1 你认为我们应该如何研究函数的图象和性质？
2．类比探究二次函数 y = ax 的图象和性质
问题2 类比一次函数的研究内容和研究方法，画出二次函 数 y = x 2 的图象，你能说说它的图象特征和性质吗？
2
一次函数的图象是一条直线，二次函数 的图象是什么形状呢？通常怎样画一个函数 的图象？
y x2
抛物线 顶点坐标
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

f1(x) = -2×x×x -1 g1(x) = 2

×x×x
a < 0，开口都向下; 对称轴都是y轴; 增减性相同.
y=-2x2
只是开口 大小不同 y=- 1 x2 二次项系数越小， 2 2 y=-x 开口越小
当a>0时,抛物线的开口向上, 顶点是抛物线的最低点,a越大, 抛物线的开口越小
y=x2的图像叫做抛物线y=x2. y=－x2的图像叫做抛物线y=－x2.
y=x2 x 实际上,二次函数的图像 它们的开口向上或者向下. 都是抛物线. 一般地,二次函数y=ax2+bx+c 的图像叫做抛物线y=ax2+bx+c. 还可以看出,二次函数y=x2和y=－x2的图像 都是轴对称图形,y轴是它们的对称轴. 抛物线与对称轴的交点(0,0)叫做抛物线的顶点. 抛物线y=x2的顶点(0,0)是它的最低点. 抛物线y=－x2的顶点(0,0)是它的最高点. o
1 2 y x 2
-5 -4 -3 -2 -1 o 1 2 3 4 5
x
2 例2.画出函数y=x2、y=2x2、y= 1 2 x 的图象：
探究
顶点坐标
y=2x2
y=x2 y= 2 x2
1
a>0，开口都向上; 对称轴都是y轴; 增减性相同
只是开口 大小不同 二次项系数越大， 开口越小 顶点都是原点(0,0)
(1) y=3x-l
(4) y=x-2
Байду номын сангаас
(2) y=2x² ＋7
(5) y=(x+3)² -x² (6) y=3(x-1)² +1
直线 ， (1) 一次函数的图象是一条_____ (2) 通常怎样画一个函数的图象？ 列表、描点、连线 (3) 二次函数的图象是什么形 状呢？ 结合图象讨论性质是数形结合的研究函数的重要方法．我们得从 最简单的二次函数开始逐步深入地讨论一般二次函数的图象和性质．
-5 -4 -3 -2 -1 o 1 2 3 4 5 x -1 -2 -3 -4 -5 -6 2 y= － x -7 -8 -9 -10
从图像可以看出,二次函数y=x2和y=－x2的图像都 是一条曲线,它的形状类似于投篮球或投掷铅球时球在 y y 空中所经过的路线. o x 这样的曲线叫做抛物线.
请同学们把所学的二次函数图象的知识归纳小结。
y=ax2 顶点 对称轴 开口 (0,0)
图象
左侧 右侧
x y x y
a＞0 最低点
(0,0) a＜0 最高点
y轴
向上
增 减 增增 大 小 大大
y轴
向下
增 增 增减 大 大 大小
思考题
已知抛物线y=ax2经过点A（-2，-8）
（1）求此抛物线的函数解析式； （2）判断点B（-1，- 4）是否在此抛物线上。 解（1）把（-2，-8）代入y=ax2,得 -8=a(-2)2,解出a= -2,所求函数解析式为 y= -2x2. （2）因为 4 2(1) 2，所以点B（-1 ，-4） 不在此抛物线上。
画函数y=x2的图像 解: (1) 列表 x … -3 -2 -1 (2) 描点 y=x2 … 9 4 1 (3) 连线
0 0
10 9 8 7 6 5 4 3 2 1 y
1 1
2 4
3 … 9 …
y=x2
还记得如何用 根据表中 x,y 的数值在 描点法画一个函数 坐标平面中描点 (x,y), 的图像吗?
一般地,抛物线y=ax2的对称轴是y轴,顶点是原点. y 2x a>0 y x y
2
2
当a<0时,抛物线的开口向 a<0 y 1 上,顶点是抛物线的最高点,a越 -5-4-3-2-1 -1o1 2 3 4 5 -2 小,抛物线的开口越小; -3
在同一坐标系内,抛物线y=ax2与 抛物线y=－ax2是关于x轴对称的.
当x=0时,最大值为0
探究
在同一坐标系中作二次函数y= x2和y=2x2的图象，会是什么样?
1 2 例1.在同一直角坐标系中画出函数y= 2 x 和y=2x2的图像 解:(1) 列表 x … -4 -3 -2 -1 0 1 2 3 4 …
(2) 描点
y= 2 x2
1
… 8 4.5 2 0.5 0 0.5 2 4.5 8 …
对称轴、顶点、最低点、最高点
yx
2
这条抛物线关于 y轴对称，y轴就 是它的对称轴.
对称轴与抛物 线的交点叫做 抛物线的顶点.
yx
2
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
抛物线 y=x2在x轴上方 (除顶点外)，顶点是它的最 低点，开口向上，并且向上 无限伸展; 当x=0时,函数 y的值最小， 最小值是0.
y x2
10 1 9 y x2 8 2 7 6 5 4 3 2 1 -5-4-3 -2-1 o1 2 3 4 5 x
x
-4 -5 -6 -7 -8 -9 -10y 2x2
1 y x2 2
1. 二次函数的图像都是抛物线.
2. 抛物线y=ax2的图像性质: (1) 抛物线y=ax2的对称轴是y轴,顶点是原点. (2)当a>0时,抛物线的开口向上,顶点是 抛物线的最低点; 当a<0时,抛物线的开口向下,顶点是 抛物线的最高点; |a|越大,抛物线的开口越小;
二次函数y=ax2的图象和性质
yx
2
8
y 2 x2
6
4 2
1 2 y x 2
2
4
－4
－2
二次函数:
一般地,形如 y=ax2+bx+c(a、b、c为常数,a≠0)的函 数,叫做二次函数.其中,x是自变量,a,b,c分别是函数表 达式的二次项系数、一次项系数和常数项.
下列哪些函数是二次函数？哪些是一次函数？
(3)连线 函数y=与函数y=－x2(图中虚线图形) 的图像相比,有什么共同点和不 同点?
1 2,y=-2x2的图像 x 2
1
y
-5 -4 -3 -2 -1 o 1 2 3 4 5 x -1 -2 -3 -4 -5 -6 -7 1 -8 y x2 2 -9 -10 y 2 x 2
2的图象： 例3.画出函数y=-x2、y=-2x2、y=- 1 x 2
1 2 在同一直角坐标系中画出函数y=－2 x 和y=－2x2的图像 解:(1)列表 x … -4 -3 -2 -1 0 1 2 3 4 …
(2)描点
y= -
1 x2 … -8 -4.5 -2 -0.5 0 -0.5 -2 -4.5 -8 2
…
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 … y=－2x2 … -8 -4.5 -2 -0.5 0 -0.5 -2 -4.5 -8 …
抛物线 y= -x2在x轴下方(除顶点外)，顶点 是它的最高点，开口向下，并且向下无限伸展， 当x=0时，函数y的值最大，最大值是0.
y
y x
2
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
y x2
y = x2、y= - x2
y x2
抛物线 顶点坐标 对称轴 位置 开口方向 增减性 最值
-1.5
x … -2 y=2x2 … 8
-1 -0.5 0 0.5 1
y
4.5 2 0.5
1.5 2 … 0 0.5 2 4.5 8 …
10 y 2 x 9 8 7 6 5 4 3 2 1
2
(3) 连线 x21 ,y=2x2的图像
函数y= 2 与函数y=x2(图中虚线图形) 的图像相比,有什么共同点 和不同点?
y = x2 （ 0， 0） y轴
在x轴上方(除顶点外)
y = - x2 （ 0， 0） y轴
在x轴下方( 除顶点外)
向上
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
向下
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
当x=0时,最小值为0
再用平滑曲线顺次连 接各点,就得到y=x2的 图像.
-5 -4 -3 -2 -1 o 1 2 3 4 5
x
请画函数y=－x2的图像 解:(1) 列表 x … -3 -2 -1 0 1 2 3 … (2) 描点 y=-x2 … -9 -4 -1 0 -1 -4 -9 … (3) 连线
1 y
根据表中x,y的数值在 坐标平面中描点(x,y), 再用平滑曲线顺次连接 各点,就得到y=-x2的图 像.
y
a>0
o
x
a<0
1、函数y=2x2的图象的开口 向上 ,对称轴y轴,顶点是(0,0);
(0,0); 2、函数y=－3x2的图象的开口向下 ,对称轴y轴,顶点是
m2+m
已知 y =(m+1)x 是二次函数且其图象开口向上, 求m的值和函数解析式 ① 解: 依题意有: m+1>0 m2+m=2 ②
解②得:m1=－2, m2=1 ∴ m=1 由①得:m>－1 此时,二次函数为: y=2x2,