转动定律的推导

刚体转动定律引言刚体转动定律是描述刚体绕固定轴进行旋转时运动规律的物理定律。

在刚体力学中，刚体是指其内部各点的相对位置保持不变的物体。

刚体转动定律主要包括角动量守恒、角加速度与力矩之间的关系以及转动惯量等内容。

本文将从这些方面对刚体转动定律进行详细介绍。

角动量守恒角动量是描述旋转物体运动状态的重要物理量，定义为质点或刚体绕某一轴线旋转时，其线性动量相对于该轴线的偏离程度。

在没有外力作用下，系统的角动量守恒。

角动量L可以表示为L = Iω，其中I是物体的转动惯量，ω是物体的角速度。

根据角速度ω = Δθ/Δt可以得到L = IΔθ/Δt。

当一个刚体受到外力矩作用时，根据牛顿第二定律可以得到F = ma，同样地，在角度上也有τ = Iα。

其中τ表示力矩，I表示物体的转动惯量，α表示物体的角加速度。

当刚体绕固定轴转动时，如果外力矩为零，则根据牛顿第二定律可以得到τ = 0，进而推导出Iα = 0。

由此可见，在没有外力矩作用下，刚体的角加速度为零，即角动量守恒。

转动惯量转动惯量是描述物体对于旋转运动的惯性大小的物理量。

对于一个质点来说，其转动惯量可以表示为I = mr²，其中m是质点的质量，r是质点到轴线的距离。

对于一个复杂形状的刚体来说，其转动惯量则需要通过积分计算得到。

对于连续分布的物体来说，其转动惯量可以表示为I = ∫r²dm。

不同形状和布局的刚体具有不同的转动惯量。

例如，对于一个围绕自身中心垂直旋转的圆盘来说，其转动惯量可以表示为I = ½MR²，其中M是圆盘的质量，R是圆盘半径。

角加速度与力矩之间的关系当刚体受到外力矩作用时，根据牛顿第二定律可以得到τ = Iα。

这个关系描述了力矩和角加速度之间的关系。

对于一个质点来说，其角加速度可以表示为α = τ/I，其中τ是作用在质点上的力矩，I是质点的转动惯量。

对于一个复杂形状的刚体来说，其转动惯量不仅与质量有关，还与物体的形状和布局有关。

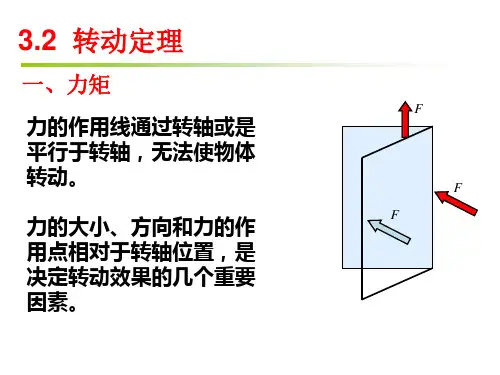
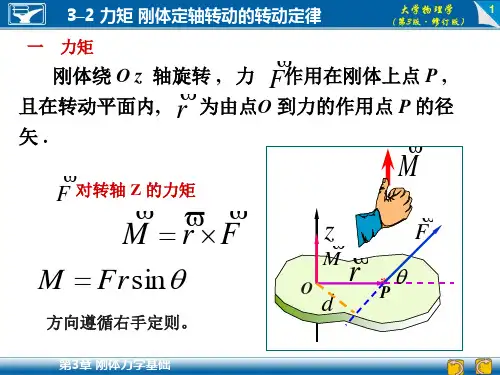
刚体的定轴转动定律1. 引言刚体是物理学中的重要概念，它是由无穷多个质点组成的一个物体，质点间的距离在运动过程中保持不变。

刚体的运动可以分为平动（刚体作为一个整体的直线运动）和转动两种。

本文将着重讨论刚体的转动运动，特别是定轴转动定律。

2. 定轴转动定轴转动是指刚体绕固定轴线进行转动的现象。

例如，摆锤在一根细线上摆动、地球自转等都是定轴转动的例子。

在定轴转动中，我们需要了解刚体受力及其运动规律。

3. 转动定律的基本概念在讨论转动定律之前，我们先来了解一些基本概念：•角度：表示物体转动的程度，常用弧度制表示，符号为θ。

•角速度：表示物体单位时间内转过的角度，常用弧度/秒表示，符号为ω。

•角加速度：表示物体单位时间内角速度的变化率，常用弧度/秒^2表示，符号为α。

•转动惯量：表示刚体对转动的惯性大小，常用字母I表示。

4. 转动定律的表述转动定律是描述刚体转动运动情况的基本定律，其中最著名的有三个定律，即牛顿定律。

它们分别是：第一定律：角动量守恒定律“在没有外力作用下，刚体的角动量保持不变。

”所谓角动量守恒，就是指一个刚体在没有外力作用下的转动过程中，其角动量保持不变。

即刚体绕某一轴线转动时，如果没有外力矩作用，那么刚体的角动量始终保持恒定。

第二定律：动能定理“刚体的角动能变化等于外力矩做功的大小。

”对于旋转的刚体来说，其具有转动惯量以及角速度，因此可以存在角动能。

根据动能定理，一个刚体的角动能的变化等于作用在刚体上的外力矩所做的功。

第三定律：力矩定律（欧拉定律）“刚体转动的加速度与合外力矩成正比，与刚体转动惯量成反比。

”欧拉定律指出了刚体转动的加速度与作用力矩的关系，其数学表达式为：τ = I * α其中，τ表示作用在刚体上的合力矩，I表示刚体的转动惯量，α表示刚体的角加速度。

5. 转动定律的应用转动定律在物理学中有广泛的应用，以下是几个常见的应用场景：•摆锤运动：根据转动定律，可以推导出摆锤的周期与摆长、重力加速度的关系。

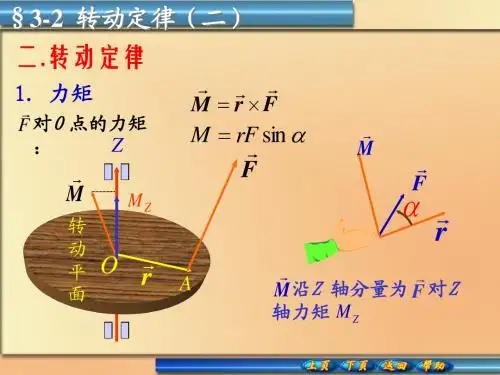
转动定律的推导 设刚体转动如图
作用在刚体上的外力为F ，取刚体上任一质量为m i 的小块。

把作用在该物块上的外力分解为两个方向上的力：径向力和切向力。

由于是刚体，物体不会发生形变，所以在径向不会产生运动。

忽略径向力的作用
对小物块运用牛顿第二定律有：ϕθsin cos i i i i it F F a m F ===
角标t 的含义为指明是作用中的切向力分量，
等号两边同乘r i ,有sin i i i it i Fr m a r ϕ=
将公式中的线量表达改写成角量，2sin i i i it i i i i i i Fr m a r m rr m r ϕββ===
其中sin i i Fr ϕ与力矩的定义吻合，所以公式可以改写为2i i i M m r β=
这是对刚体中的一个小质元的公式，考虑整个刚体，对上式两边求和有
2i i i
i i M m r β→∞→∞=∑∑ 公式左边为合外力矩。

令2i i mr J =∑，考虑到β与位置无关，上式改写为
M J β= ---1，
写为矢量形式 M J β= ---2
公式1，2即为刚体的转动定律，它是牛二定律在刚体转动问题上的变形。

∑∑∑∑===222222
12121r m r m m E i i i ik ωωv 22
1ωJ E k =。

几种常见刚体转动惯量公式推导刚体是一个物体在没有外力作用下不发生形变的状态。

它的转动惯量是描述物体在转动过程中受到惯性力的难易程度的物理量。

在很多物理问题中，都需要根据具体的几何形状和质量分布计算刚体的转动惯量。

以下是几种常见的刚体转动惯量公式推导。

1.点质量的转动惯量一个质量为m的点，固定在轴上转动。

它的转动惯量可以用公式I=mr²来计算。

其中，r是点到轴的距离。

推导：在转动过程中，点质量只有一个轴向的距离变化，因此它的转动惯量可以表示为I=m(Δr)²。

又根据转动定律，I=FΔt，其中F 是惯性力，Δt是时间。

对于点质量，惯性力和轴向距离的乘积恒为mr，因此I=mr²。

2.杆的转动惯量一个质量为m、长度为L的均匀杆，绕过它的重心垂直于杆的轴旋转。

它的转动惯量可以用公式I=1/12mL²来计算。

推导：对于均匀杆，在其自身的中心点处，质心和转轴重合。

因此我们可以将杆的质量分成若干个小块，对每个小块计算旋转惯量再相加。

设小块的质量为dm，位置为x，则小块的旋转惯量为dI=xdm，总的旋转惯量为I=∫xdm。

对于均匀杆，在L/2左右有一个质心，所以我们可以将积分限定在-L/2到L/2之间。

因为每段长度为dx的小块质量都相等，所以可以将积分转化为∫xdx。

得到I=1/12mL²。

3.球的转动惯量一个半径为r、质量为m的球绕通过球心的轴旋转。

它的转动惯量可以用公式I=2/5mr²来计算。

推导：在球内部的所有点，它们与轴的距离是相等的。

我们可以将球的质量分成若干个小块，对每个小块计算旋转惯量再相加。

设小块的质量为dm，距离轴的距离为r，则小块的旋转惯量为dI=r²dm，总的旋转惯量为I=∫r²dm。

在球体内，每个小块的质量都相同，所以可以将积分转换为∫r²dV，其中V是球的体积。

将球的质量和体积表示成m和(4/3)πr³，得到I=2/5mr²。

转动定律与角动量守恒转动定律和角动量守恒是力学中重要的概念，用于描述物体在转动过程中的行为和性质。

转动定律主要由牛顿第二定律推导而来，而角动量守恒是由系统中的角动量守恒定律得出的。

本文将详细讨论转动定律和角动量守恒的原理和应用。

一、转动定律在力学中，转动定律描述了物体在转动过程中所受到的力矩与加速度之间的关系。

根据牛顿第二定律（力矩等于质量乘以加速度），我们可以得到以下转动定律的表达式：1. 转动惯量转动惯量是描述物体对转动的惯性大小的物理量，用字母I表示。

对于不同形状和质量分布的物体，其转动惯量的计算方法也不相同。

比如，对于质量均匀分布的细长杆，其转动惯量可以通过公式I=1/12×m×L²来计算，其中m是杆的质量，L是杆的长度。

2. 角加速度和力矩的关系在转动定律中，角加速度和力矩之间存在着简单的线性关系。

根据转动定律的表达式，力矩等于转动惯量乘以角加速度，可以表示为τ=I×α，其中τ表示力矩，α表示角加速度。

3. 角动量和力矩的关系角动量描述了物体在转动过程中的旋转状态，其大小与转动惯量和角速度的乘积成正比。

根据转动定律的表达式，角动量等于转动惯量乘以角速度，可以表示为L=I×ω，其中L表示角动量，ω表示角速度。

二、角动量守恒角动量守恒是描述系统中角动量不变的物理原理，适用于没有外力和力矩作用的封闭系统。

当系统中没有外力和力矩作用时，系统的总角动量保持不变。

1. 系统的总角动量系统的总角动量是指系统中所有物体角动量的矢量和。

当系统中有多个物体时，每个物体的角动量可以用L=I×ω的表达式计算，然后将所有物体的角动量矢量相加，得到系统的总角动量。

2. 角动量守恒当系统中没有外力和力矩作用时，系统的总角动量保持不变。

这意味着，系统中每个物体的角动量之和在转动过程中不会发生改变。

三、转动定律与角动量守恒的应用转动定律和角动量守恒在实际问题中具有广泛的应用。

转动定律与角动量的变化转动定律和角动量是物理学中重要的概念，它们描述了物体在转动过程中的运动规律和角动量的变化情况。

本文将介绍转动定律和角动量的概念，并探讨它们之间的关系以及在不同情况下的变化特点。

一、转动定律的概念转动定律是描述刚体在受到外力作用下，围绕某一轴心转动的运动规律。

根据转动定律，物体的转动是由外力矩（也称为转动力矩）引起的，它的大小与物体受力点到转轴的距离和作用力的大小成正比。

根据转动定律，我们可以得到以下公式：M = Iα其中，M是物体的外力矩，I是物体的转动惯量，α是物体的角加速度。

根据这个公式，我们可以看出，当外力矩和转动惯量增大时，物体的角加速度也会增大。

二、角动量的概念角动量是描述物体转动状态的物理量，它定义为物体的转动惯量与角速度的乘积。

角动量的大小与物体的转动惯量和角速度的大小成正比。

角动量的公式如下：L = Iω其中，L是物体的角动量，I是物体的转动惯量，ω是物体的角速度。

从这个公式可以看出，当物体的转动惯量或角速度增大时，角动量也会增大。

三、转动定律与角动量的关系转动定律和角动量之间存在着密切的关系。

根据牛顿第二定律和定义的角动量，我们可以推导出转动定律与角动量之间的关系式：M = dL/dt其中，M是物体所受的外力矩，L是物体的角动量，dt表示时间的微元。

这个关系式表明，外力矩的变化率等于角动量对时间的导数。

也就是说，外力矩的改变会引起角动量的变化。

四、转动定律和角动量的变化特点在不同情况下，转动定律和角动量的变化特点也有所不同。

1. 自由转动：在没有外力矩作用下，刚体围绕固定转轴自由转动。

此时，根据转动定律，外力矩为零，物体的角速度保持恒定不变。

同时，根据角动量守恒定律，角动量也保持不变。

2. 施加力矩：当在自由转动过程中施加力矩时，根据转动定律，物体将受到额外的外力矩，从而改变角速度和角动量的大小。

施加的外力矩越大，角速度和角动量的增加越明显。

3. 轴心移动：如果转轴自身发生移动，根据转动定律和角动量的守恒定律，物体将受到额外的外力矩，导致角速度和角动量的变化。

非定轴转动定律
1. 非定轴转动定律的表述:
物体绕任意一条不固定的轴线旋转时,其角加速度与所受合外力矩成正比,并与转动惯量成反比。

2. 数学表达式:
α = Στ / I
其中:
α - 角加速度(rad/s²)
Στ - 所有外力矩的矢量和(N·m)
I - 物体绕旋转轴线的转动惯量(kg·m²)
3. 特殊情况:
- 当外力矩为零时,物体保持匀速旋转或静止不动。

- 当外力矩不为零时,物体将产生角加速度,进行加速或减速旋转运动。

4. 应用实例:
非定轴转动定律广泛应用于分析各种旋转系统的运动,如陀螺仪、旋转飞镖、开启的门、旋转木马等。

通过计算所受外力矩和转动惯量,可以预测和控制这些系统的角加速度。

非定轴转动定律是研究旋转运动的关键理论,对于工程设计、天文学、机器人技术等领域都有重要应用。

掌握该定律有助于深入理解和分析复杂的旋转现象。