6.刚体定轴转动定律电子教案
- 格式：doc
- 大小：197.50 KB
- 文档页数：7
下载文档原格式
合集下载
第5章 刚体的定轴转动
（1） 式中n表示转动方向，ω表示角速度的大小。 2、角加速度矢量
角加速度矢量定义为
（2） 显然，若角加速度矢量的方向与角速度矢量的方向相同，见下图 （a），则角速度在增加；反之，若角加速度与角速度的方向相反，见 下图（b），则角速度在减小。从图（a）、（b）中不难验证，角加速 度矢量的方向与直观转动的加速方向也构成右手螺旋关系。既当四个手 指指向直观的加速方向时，大姆指所指向的方向即为角加速度矢量的方 向。
(4) 其中
为各分力的力矩，证毕。 由于作用力和反作用力是成对出现的，所以它们的力矩也成对出
现。由于作用力与反用力的大小相等，方向相反且在同一直线上因而有 相同的力臂，见下图，所以作用力矩和反作用力矩也是大小相等，方向 相反，其和为零。
(5)
作用力矩和反作用力矩 二、刚体对定轴的角动量
在刚体的定轴转动中，刚体对定轴的角动量是一个很重要的物理 量，在很多问题的分析中都要用到这个概念，下面我们来讨论这个问 题。 刚体绕定轴转动时，它的每一个质点都在与轴垂直的平面上运动。下面 我们先分析质点对定轴的角动量，而且只考虑质点在轴的垂面上运动的 情况。如下图所示，有一质点在z轴的垂面M内运动，质点的质量为m， 对z轴（即对质点转心）的矢径为r，速度为v，动量p=mv。如同在角动 量知识点中讨论的一样，我们定义质点对定轴的角动量为
第5章 刚体的定轴转动 ◆ 本章学习目标 理解：刚体、刚体转动、转动惯量的概念；刚体定轴转动定律及角动量守
恒定律。 掌握：转动惯量，转动中的功和能的计算；用刚体定轴转动定律及角动量
守恒定律求解定轴转动问题的基本方法。 ◆ 本章教学内容
1．刚体的运动 2．刚体定轴转动定律 3．转动惯量的计算 4．刚体定轴转动定律的应用 5．转动中的功和能 6．对定轴的角动量守恒 ◆ 本章重点 刚体转动惯量的物理意义以及常见刚体绕常见轴的转动惯量； 力矩计算、转动定律的应用； 刚体转动动能、转动时的角动量的计算。 ◆ 本章难点 力矩计算、刚体转动过程中守恒的判断及其准确计算。
角加速度矢量定义为
（2） 显然，若角加速度矢量的方向与角速度矢量的方向相同，见下图 （a），则角速度在增加；反之，若角加速度与角速度的方向相反，见 下图（b），则角速度在减小。从图（a）、（b）中不难验证，角加速 度矢量的方向与直观转动的加速方向也构成右手螺旋关系。既当四个手 指指向直观的加速方向时，大姆指所指向的方向即为角加速度矢量的方 向。
(4) 其中
为各分力的力矩，证毕。 由于作用力和反作用力是成对出现的，所以它们的力矩也成对出
现。由于作用力与反用力的大小相等，方向相反且在同一直线上因而有 相同的力臂，见下图，所以作用力矩和反作用力矩也是大小相等，方向 相反，其和为零。
(5)
作用力矩和反作用力矩 二、刚体对定轴的角动量
在刚体的定轴转动中，刚体对定轴的角动量是一个很重要的物理 量，在很多问题的分析中都要用到这个概念，下面我们来讨论这个问 题。 刚体绕定轴转动时，它的每一个质点都在与轴垂直的平面上运动。下面 我们先分析质点对定轴的角动量，而且只考虑质点在轴的垂面上运动的 情况。如下图所示，有一质点在z轴的垂面M内运动，质点的质量为m， 对z轴（即对质点转心）的矢径为r，速度为v，动量p=mv。如同在角动 量知识点中讨论的一样，我们定义质点对定轴的角动量为
第5章 刚体的定轴转动 ◆ 本章学习目标 理解：刚体、刚体转动、转动惯量的概念；刚体定轴转动定律及角动量守
恒定律。 掌握：转动惯量，转动中的功和能的计算；用刚体定轴转动定律及角动量
守恒定律求解定轴转动问题的基本方法。 ◆ 本章教学内容
1．刚体的运动 2．刚体定轴转动定律 3．转动惯量的计算 4．刚体定轴转动定律的应用 5．转动中的功和能 6．对定轴的角动量守恒 ◆ 本章重点 刚体转动惯量的物理意义以及常见刚体绕常见轴的转动惯量； 力矩计算、转动定律的应用； 刚体转动动能、转动时的角动量的计算。 ◆ 本章难点 力矩计算、刚体转动过程中守恒的判断及其准确计算。
刚体的定轴转动及转动定律PPT学习教案
；（3）t = 6 s 时飞轮边缘上一点的线速度、切向加速度和法
向加速度 .
解：
（1）
5π rads , 1
t = 30 s 时，
0
0.
设 t= 0s
时，
.飞轮做匀减速运动
0 0
0 0 5π rad s1 π rad s2
t
30
6
飞轮 30 s 内rad 2 2 (π 6)
解：
dm dV 2 r h dr
其中：
m m
V r 2 h
所以：
J r 2 dv m
R 2rh r 2dr
0
1 mR2
2
第24页/共28页
第25页/共28页
四 平行轴定理 质量为 的刚体，如果对其质心轴的转动惯量 为 ，则对任一与该轴平行，相距为 的转轴的转动惯量为：
0.105
m s2
an r 2 0.2´ (4 π)2 m ×s2 31.6 m ×s2
第10页/共28页
例2 在高速旋转的微型电机里，有一圆柱形转子可绕垂直其横截
面后通，过其中转心速的达轴到转18动00.0开r·m始in时-1，. 已它知的转角子速的度角加0 速度0与，时经间3成00正s 比
第12页/共28页
一 力矩 刚体上P点的力 对转轴 Z 的力矩为：
大小： 方向：右手定则
例
F
M rF
M
M Fr sin Fd
F
F
Fi 0 , Mi 0
F
F
z
M
r
O
d
F *P
Fi 0 , Mi 0
第13页/共28页
讨论 1）若力 不在转动平面内
则：
刚体教案
( m 2 m 1) g β = m m m ( 1 + 2 + 2 )r
m m 1( 2 m 2 + 2 ) g m 2( 2 m 1 + 2 ) g T 1= T 2= m m 1+ m 2 + 2 m 1+ m 2 + m 2
m
已知：R = 0.2 m ， m =1 kg ，v o = 0， h =1.5 m 绳轮无相对滑动，绳不可伸长，下落时间 t =3 s 。
m r
T 2 , a , β.
T1
T2 m2
m +
m1 T1
β a T2
T2 m2
T1 m1
列方程
a
m1 g
m2 g
T2 r T1 r = J β m2g T 2 =m2a T 1 m 1g = m 1a
受力分析
1 J= m r 2 2
a = rβ
m2 m1 ) g ( a= m m m ( 1+ 2 + 2 )
J r dm r 2 dm mr 2
2
m
ω r
[ 例3 ]质量为m，半径为R 的均质圆盘的转动惯量0
任取面元ds（离r远处dr宽细环）
质量dm=dS
2
dm 2rdr
2
3
m / R
3
ω
dJ r dm 2r dr
1 2 J 2r dr mR 2 0
M M θ
刚体的定轴转动可以用 角量描述：各质点角动量 相同
1.定轴转动的角量
角位移： θ 方向： 角速度：
d
r M 0 θ
d
ˆ d dt
刚体定轴转动的动量矩定理和动量矩守恒
2
6m(2gh)1 2 (m 6m)l
演员 N 以 u 起 跳, 达到的高度
h u 2 l 2 2 ( 3m )2 h
2g 8g m 6m
第11页/共15页
例4 质量很小长度为l 的均匀细杆,可绕过其中心 O 并与纸面垂直的轴在竖直平面内转动.当细杆静止于水平
位置时, 有一只小虫以速率v0 垂直落在距点O为 l/4 处, 并
即：刚体所受的外力矩等于动量矩对时间的变化率。
Mdt dL
t2
t1
Mdt
J2
J1
∴作用于刚体上冲量矩等于刚体动量矩的增量。
第3页/共15页
三、刚体定轴转动的动量矩守恒
若 M 0，则
dL 0 dt
L L0 J 常量
讨论
➢ 守 恒条件
M 0
➢ 内力矩不改变系统的动量矩.
➢ 在冲击等问题中 M in M ex L 常量
第5页/共15页
动量矩守恒定律在技术中的应用
惯性导航仪（陀螺）
第6页/共15页
被中香炉
例1：质量为m1，长为l的均匀直棒，可绕垂直于棒 的一端的水平轴O无摩擦的转动，它原来静止在水
平位置处，现在一质量为m2的弹性小球飞来，正好 在棒的下端与棒垂直相撞，撞后，棒从平衡位置处
摆动达到最大角度 30o , 求：
M dL d(J) dJ
dt dt
dt
即
mgr cos d ( 1 ml2 mr2 ) 2mr dr
dt 12
dt
考虑到 t
dr g cost 7lg cos(12v0 t)
dt 2
24 v0
7l
第13页/共15页
第14页/共15页
教学设计：定轴转动刚体的角动量守恒定律及其应用
问题1：单旋翼直升机为什么要有尾翼装置？双旋翼直升机为什
么设计两个机翼？两个机翼的旋转方向有什么关系？
、播放一段花样滑冰和跳水的视频，提醒学生注意观察运动员的肢体动作。
d J t d t =
（类比：d d P F t
=外）
21
d t 为M 冲量矩。
说明： （1）冲量矩是矢量
角动量定理：合外力矩对刚体的冲量矩等于刚体角动量的增量。
定轴转动刚体的角动量守恒定律=
角动量守恒定律：当合外力矩等于零，刚体的角动量保持不变。
，与内力矩无关；ω均变，但对定轴的角动量守恒定律的应用
多个刚体组成的系统： M =外i i L J ω=∑=恒量
双旋翼直升机：装置反向转动的双旋翼产生反向角 动量
0 , L Jω==
外=恒量0 , P mv
===恒量
课后思考题：
（1）为什么猫从高处落下时总能四脚着地？（视频）
（2）航天器在对接时是如何实现姿态控制的？（图片）。
大学物理上册《刚体定轴转动》PPT课件
刚体性质
刚体是一个理想化的物理模型，实际物体在受到力的作用时， 都或多或少地会变形，但如果变形很小，对研究问题的影响可 以忽略不计时，就可以把这个物体看成刚体。
定轴转动描述
定轴转动
刚体上所有质点都绕同一直线作圆周运动，这种运 动叫做刚体的定轴转动。这条直线叫做刚体的转轴。
转动的快慢
用角速度ω来描述刚体转动的快慢，单位时间内转 过的角度θ越大，角速度ω就越大。
转动能定理
刚体定轴转动时，合外力矩对刚体所做的功等于刚体转动动能的增 量。
转动动能的计算
转动动能Ek等于刚体的转动惯量I与角速度ω平方的一半的乘积，即 Ek=1/2Iω²。
应用举例
通过计算合外力矩对刚体所做的功，可以求解刚体在某个过程中的角 速度、角加速度等物理量。
动力学普遍定理在转动中应用
动力学普遍定理
VS
误差分析
分析实验过程中可能产生的误差来源，如 测量误差、仪器误差等，并提出减小误差 的方法。
实验结果讨论和改进建议
实验结果讨论
根据实验数据和分析结果，讨论刚体定轴转动的基本规律以及实验过程中存在的问题和不足之处。
改进建议
提出改进实验方法和提高实验精度的建议，如优化实验器材、改进测量方法等。
05
动能定理揭示了力对刚体所做 的功与刚体动能变化之间的关 系；机械能守恒定律则指出在 只有重力或弹力做功的情况下， 刚体的机械能保持不变。
常见题型解题技巧分享
选择题答题技巧
注意审清题意，明确题目要求；对于概念性选择题，要准确理解相关概念；对于计算性选择题，要善于运用 物理规律和公式进行推理和计算。
填空题答题技巧
未来发展趋势预测
高效能源利用
随着能源问题的日益突出，未来旋转机构将更加注重高效能 源利用，如采用新型材料、优化结构等降低能耗。
刚体是一个理想化的物理模型，实际物体在受到力的作用时， 都或多或少地会变形，但如果变形很小，对研究问题的影响可 以忽略不计时，就可以把这个物体看成刚体。
定轴转动描述
定轴转动
刚体上所有质点都绕同一直线作圆周运动，这种运 动叫做刚体的定轴转动。这条直线叫做刚体的转轴。
转动的快慢
用角速度ω来描述刚体转动的快慢，单位时间内转 过的角度θ越大，角速度ω就越大。
转动能定理
刚体定轴转动时，合外力矩对刚体所做的功等于刚体转动动能的增 量。
转动动能的计算
转动动能Ek等于刚体的转动惯量I与角速度ω平方的一半的乘积，即 Ek=1/2Iω²。
应用举例
通过计算合外力矩对刚体所做的功，可以求解刚体在某个过程中的角 速度、角加速度等物理量。
动力学普遍定理在转动中应用
动力学普遍定理
VS
误差分析
分析实验过程中可能产生的误差来源，如 测量误差、仪器误差等，并提出减小误差 的方法。
实验结果讨论和改进建议
实验结果讨论
根据实验数据和分析结果，讨论刚体定轴转动的基本规律以及实验过程中存在的问题和不足之处。
改进建议
提出改进实验方法和提高实验精度的建议，如优化实验器材、改进测量方法等。
05
动能定理揭示了力对刚体所做 的功与刚体动能变化之间的关 系；机械能守恒定律则指出在 只有重力或弹力做功的情况下， 刚体的机械能保持不变。
常见题型解题技巧分享
选择题答题技巧
注意审清题意，明确题目要求；对于概念性选择题，要准确理解相关概念；对于计算性选择题，要善于运用 物理规律和公式进行推理和计算。
填空题答题技巧
未来发展趋势预测
高效能源利用
随着能源问题的日益突出，未来旋转机构将更加注重高效能 源利用，如采用新型材料、优化结构等降低能耗。
力矩刚体绕定轴转动定律课件
03
力矩刚体绕定轴转动的实际应用
日常生活中的应用实例
自行车轮转动
方向盘控制
当我们在骑自行车时，脚踏板施加的 力量通过链条传递到车轮上，使车轮 发生转动。
在驾驶汽车时，我们通过转动方向盘 来控制车辆的方向，方向盘的转动就 是力矩刚体绕定轴转动的实例。
门把手转动
当我们握住门把手转动时，门被推开 或关闭，这是由于门把手施加的力矩 使门发生转动。
力矩的大小决定了刚体转动的速度，力矩 越大，刚体的角速度越快。
刚体转动惯量的概念
01
02
03
转动惯量定义
转动惯量是描述刚体转动 惯性大小的物理量，与刚 体的质量分布和转动轴的 位置有关。
计算公式
对于质量均匀分布的刚体 ，转动惯量I = (1/2) * m * r^2，其中m是质量，r 是到转动轴的距离。
实验结果分析和结论
实验结果分析
通过实验数据，分析角速度与力矩之间的关系，验证力矩刚体绕定轴转动定律 。同时，比较不同转动惯量下刚体的角速度变化，加深对转动惯量影响的理解 。
实验结论
通过实验验证，可以得出力矩刚体绕定轴转动定律的正确性。同时，实验结果 也表明转动惯量对刚体的角速度有影响，转动惯量越大，相同力矩作用下刚体 的角速度越小。
05
力矩刚体绕定轴转动定律的深入探讨
力矩刚体转动过程中的能量转换
机械能转换
力矩作用在刚体上，使刚体从静 止或匀速转动状态变为加速转动 状态，在此过程中，刚体的动能 增加，而势能保持不变。
能量守恒
力矩刚体转动过程中的能量转换 符合能量守恒定律，即输入的力 矩能量等于刚体动能的变化量。
力矩刚体转动过程中的动量守恒
工业生产中的应用实例
刚体定轴转动的转动定律
R
M
h
Hale Waihona Puke 解法一 用牛顿第二运动 定律及转动定律求解.分 析受力如图所示. 对物体m用牛顿第二 运动定律得 mg T ma 对匀质圆盘形滑轮用 转动定律有 TR J 物体下降的加速度的 大小就是转动时滑轮边缘 上切向加速度，所以
o R M
T
h
a
G
a R 物体m 落下h 高度时的速率为
2
3.试求质量为m 、半径为R 的匀质圆环 对垂直于平面且过中心轴的转动惯量. 解 作示意图如右,由于质 量连续分布，所以由转动 惯量的定义得
J R 2dm
m
dm
o
R
2R 0
m R dl 2R
2
mR 2
4.试求质量为m 、半径为R 的匀质圆盘 对垂直于平面且过中心轴的转动惯量. dr 解 如图所示, 由于质 量连续分布，设圆盘的 R l o r 厚度为l，则圆盘的质量 密度为 m 2 R l
r近日 r远日
v近日
解 彗星受太阳引力的作用，而引力通过了 太阳，所以对太阳的力矩为零，故彗星在运 行的过程中角动量守恒. 于是有 r近日 v近日 r远日 v远日 因为 r近日 v近日 ，r远日 v远日
r近日v近日 所以 r远日 v远日
代入数据可, 得
J r 2dm
m
R 0
1 1 4 r 2r ldr R l mR 2 2 2
2
5. 如图所示，一质 量为M 、半径为R 的匀 质圆盘形滑轮，可绕一 无摩擦的水平轴转动. 圆盘上绕有质量可不计 绳子，绳子一端固定在 滑轮上，另一端悬挂一 质量为m 的物体，问物 体由静止落下h 高度时, 物体的速率为多少？
动力学中的刚体转动教案
动力学中的刚体转动教案
本教案将介绍动力学中的刚体转动，包括刚体定轴转动的描述、转动定律和角动量等内容。
一、刚体定轴转动的描述
刚体定轴转动是指刚体上所有质元都绕同一直线做圆周运动，且刚体上各质元的角量（角位移、角速度、角加速度）相同，而各质元的线量（线位移、线速度、线加速度）大小与质元到转轴的距离成正比。
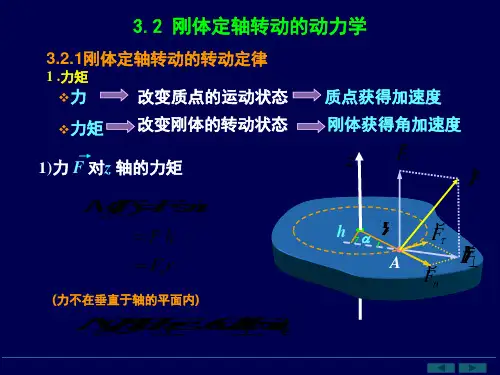
二、转动定律
转动定律是指在刚体定轴转动中，力矩是改变刚体转动状态的唯一原因。
力矩的方向垂直于转轴，并指向旋转方向。
对于一个质点在定轴上的运动，其角动量（L）等于其转动惯量（I）和角速度（ω）的乘积，即L=Iω。
当有多个质点绕同一转轴转动时，它们对转轴的角动量之和等于零。
三、角动量
角动量是指刚体绕固定轴转动的状态，其数值等于刚体对固定轴的力矩和角速度的乘积。
在不受外力矩作用时，刚体的角动量是守恒的。
当刚体受到外力矩作用时，其角动量会发生改变，改变的量等于外力矩和角速度的乘积。
四、例题解析
例如，一个质量为m的质点以角速度ω绕固定轴z轴做平面定轴转动，求该质点对z轴的角动量Lz。
根据角动量的定义，Lz=Iω，其中I是该质点的转动惯量。
由于该质点是在二维平面上运动，因此其转动惯量为I=mr²/2，其中r为质点到z轴的距离。
代入角动量的定义得到Lz=mrω/2。
五、总结
本教案介绍了动力学中的刚体转动，包括刚体定轴转动的描述、转动定律和角动量等内容。
通过例题解析，我们可以看到如何运用这些概念来解决实际问题。
在实际教学中，可以根据学生的实际情况和需求进行适当的调整和补充。
刚体的定轴转动
[思考] ①结果合理否？ (量纲OK；又： , 合理.) ②其它解法？ (转动动能定理 or 转动定律)
(3)求摆到竖直位置时端点的速度。
§5.4 定轴转动的角动量守恒定律 (The Law of Conservation of Angular Momentum About a Fixed Axis) 1.对固定轴的角动量 ⑴质点对轴的角动量
⒌ 如图，质量为m、半径为R的圆盘可绕通 过其直径的光滑固定轴转动，转动惯量 J=mR2/4，设圆盘从静止开始在恒力矩M 作用下转动，则t秒后圆盘边缘上的B点的 at = ，an= .
R B
解： M恒定 恒定 匀变速率转动 ⑴ =M/J=4M/mR2 于是 at=R=4M/mR ⑵因恒定，故有 = t=4Mt/mR2 于是 an=R2=16M2t2/m2R3
本章： 定轴转动运动学
定轴转动定律
转动中的功和能 定轴转动的角动量守恒定律
§5.1 定轴转动运动学 (Kinematics of Rotation About a Fixed Axis)
一.定轴转动: 刚体内各质点都绕同一固定不动的轴作圆 周运动. 刚体定轴转动的特点：
1）刚体上各质点都作圆运动， 但半径不一定相等。 2)与轴线垂直的园平面为转动平面. 3）刚体上各点做圆运动的半径在 相等的时间间隔内转过相同的角度， ω 、α 相等。
e.g.
细杆质量m, 长L o 则对于 oo轴，J=mL2/3 对于 cc轴，J=mL2/12
o
c c
④转动定律与牛Ⅱ比较： M～ F J ～m ～a
ii)J量度了刚体转动惯性的大小
o 讨论：
o
o
o a
a A
a
a
B C
(3)求摆到竖直位置时端点的速度。
§5.4 定轴转动的角动量守恒定律 (The Law of Conservation of Angular Momentum About a Fixed Axis) 1.对固定轴的角动量 ⑴质点对轴的角动量
⒌ 如图，质量为m、半径为R的圆盘可绕通 过其直径的光滑固定轴转动，转动惯量 J=mR2/4，设圆盘从静止开始在恒力矩M 作用下转动，则t秒后圆盘边缘上的B点的 at = ，an= .
R B
解： M恒定 恒定 匀变速率转动 ⑴ =M/J=4M/mR2 于是 at=R=4M/mR ⑵因恒定，故有 = t=4Mt/mR2 于是 an=R2=16M2t2/m2R3
本章： 定轴转动运动学
定轴转动定律
转动中的功和能 定轴转动的角动量守恒定律
§5.1 定轴转动运动学 (Kinematics of Rotation About a Fixed Axis)
一.定轴转动: 刚体内各质点都绕同一固定不动的轴作圆 周运动. 刚体定轴转动的特点：
1）刚体上各质点都作圆运动， 但半径不一定相等。 2)与轴线垂直的园平面为转动平面. 3）刚体上各点做圆运动的半径在 相等的时间间隔内转过相同的角度， ω 、α 相等。
e.g.
细杆质量m, 长L o 则对于 oo轴，J=mL2/3 对于 cc轴，J=mL2/12
o
c c
④转动定律与牛Ⅱ比较： M～ F J ～m ～a
ii)J量度了刚体转动惯性的大小
o 讨论：
o
o
o a
a A
a
a
B C
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6.刚体定轴转动定律
《大学物理》作业 No.6 刚体定轴转动定律
班级 ___________ 学号 __________ 姓名 _________ 成绩 ________
基本要求：
（1） 理解描述刚体定轴转动的基本物理量以及角量与线量之间的关系 （2） 掌握力矩、转动惯量的概念和转动定律及应用 内容提要
1. 刚体绕定轴转动的角速度和角加速度
t t t d d lim 0θ
θω=
∆∆=→∆， t d d ωβϖϖ=
2. 刚体绕定轴转动匀变速转动公式
2002
1t t αωθθ++=， t αωω+=0，)(202
02θθαωω-+=
3. 力矩F r M ϖ
ϖϖ⨯=
注意对固定点的力矩与对转轴的力矩的区别
力矩是使物体转动状态变化的原因，力是使物体平动状态变化的原因，合外力为零，合外力矩不一定为零； 4. 刚体的定轴转动定律: βϖ
ϖJ M =
5. 刚体转动惯量：质量分布不连续的质点系∑∆=2i i r m J
连续物体m r J d 2
⎰=
6. 转动惯量有关的因素：
a. 刚体的质量;
b. 质量的分布;
c. 转轴的位置; 7. 几种特殊情况的转动惯量大小：
a: 长为L 、质量为m 的均匀细棒绕一端的转动惯量:3/2mL J = b: 质量分布均匀的圆盘绕中心转轴: 22
1
mR J =
一、选择题
1. 以下说法正确的是
[ ] (A) 合外力为零,合外力矩一定为零；
(B) 合外力为零,合外力矩一定不为零； (C) 合外力为零,合外力矩可以不为零； (D) 合外力不为零,合外力矩一定不为零； (E) 合外力不为零,合外力矩一定为零.
2. 有A 、B 两个半径相同,质量相同的细圆环.A 环的质量均匀分布,B 环的质量不均匀分布,设它们对过环心的中心轴的转动惯量分别为I A 和I B ,则有 [ ] (A) I A ＞I B .
(B) I A ＜I B .
(C) 无法确定哪个大. (D) I A ＝I B . 3.将细绳绕在一个具有水平光滑轴的飞轮边缘上，如果在绳端挂一质量为m 的重物时，飞轮的角加速度为β1. 如果以拉力2mg 代替重物拉绳时, 飞轮的角加速度将
[ ] （A ）小于β 1.
(B )大于β1,小于2β1. (C) 大于2β1. (D) 等于2β1.
4. 一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮，绳的两端分别悬有质量为m 1和m 2的物体(m 1＜m 2﹚，如图所示．绳与轮之间无相对滑动．若某时刻滑轮沿逆时针方向转动，则绳中的张力 [ ] (A) 处处相等． (B) 左边大于右边．
(C) 右边大于左边． (D) 哪边大无法判断．
二、填空题
1.半径为r = 1.5m 的飞轮作匀变速转动,初角速度ω 0=10rad/s,角加速度β=－5rad/s 2, 则在t = 时角位移为零,而此时边缘上点的线速度v = .
2.半径为20cm 的主动轮,通过皮带拖动半径为50cm 的被动轮转动,皮带与轮之间无相对滑动, 主动轮从静止开始作匀角加速转动. 在4s 内被动轮的角速度达到8πrad/s,则主动轮在这段时间内转过了 圈.
3. 如图所示一长为L 的轻质细杆,两端分别固定质量为m
和2m 的小球,此系统在竖直平面内可绕过中点O 且与杆垂直的水平光滑轴(O 轴)转动, 开始时杆与水平成60°角,处于静止状态.无初转速地释放后,杆球这一刚体系统绕O 轴转动,系统绕O 轴的转动惯量J = .释放后,当杆转到水平位置时,刚体受到的合外力矩M = ; 角加速度β= .
三、计算题
m 2 m 1
O
○ 2m
○ m
O · ╮
60°
1. 质量均为m 的物体A 和B 叠放在光滑桌面上，轻绳跨过轴光滑的定滑轮连接
物体A 和B （图1）。
设定滑轮的转动惯量22
1
mR J =，（R 为滑轮半径），忽
略A 与B 间的摩擦。
今用水平力F 拉物体A ，已知m R kg m N F 05.0,0.8,10===。
求: （1）定滑轮的角加速度。
（2）物体A 与定滑轮间绳子的张力。
（3）物体B 与定滑轮间绳子的张力。
2. 两端挂着物体质量分别为m 和m 2的轻绳，跨过两质量均为m ，半径均为r 的均匀圆盘状定滑轮（图2）。
滑轮轴光滑，将系统静止释放，求两滑轮间绳子的张力。
No.6
参考答案 一、选择题
1. （C ）；
2. （D ）；
3.（C ），提示：如图设定滑轮的质量为M ，半径为R ，绕中心轴转动的转动惯量为J ，如果在绳端挂一质量为m
牛顿第二定律，对定滑轮应用转动定律，可以得到方程组
1
1ββR a J TR ma T mg ===-解得2
1R J mgR
+=β
如果以拉力2mg 代替重物拉绳时，对定滑轮应用转动定律22βJ mgR =，可得， J
mgR
22=β
比较发现122ββ>。
4. (C )
二、填空题
1. t = 4秒, v = s m /15- 提示：根据公式02
12
0=+
=t t βωθ可得t = 4秒，此时飞轮的角速度s rad t /100-=+=βωω，故边缘部分的线速度为s m R v /15-==ω ; 2. 20，提示：主动轮与被动轮在任意时刻边缘处的线速度是相等的，所以
12.085.0ωπ⋅=⋅，得到主动轮在4秒时的角速度为s rad /201πω=，所以主动轮
转过的角度为rad t t πωβθ402
1
2112===
所以主动轮转过的圈数为20240==
ππ
n ； 3. J =243ml ，M = 2mgl ，β = g L 32
，提示：不连续物体的转动惯量2
222
2
1
43424mL L m L m r m J i i i =⋅+⋅==∑=，合外力的力矩为重力矩，两物体重力矩
方向相反，为2
222mgL mg L mg L M =⋅-⋅=，根据转动定律βJ M =，可得角加速度L
g 32=
β；
三、计算题
1. 解：
β
βr a J r T r T ma T B ma T F A ==-==-122::对轮：对对
带入数据：
()β
β
β
β05.005.082
105.005.005.08:05.0810:2
1221=⨯⨯=⨯-⨯⨯=⨯=-a T T T B T A 对轮：对对 得到，N T N T s rad 6,4,/1021===β 2. 解：设两滑轮间绳子的张力为3T
βr a ma T mg m ma mg T m ==-=-22:2:21对对 又因为，
β
βJ r T r T J r T r T =-=-3213
得到，βJ r T r T T T T 2,2
122
13=-+=
带入数据得到，2
3,4521mg
T mg T =
=
所以，两滑轮间绳子的张力mg T 8
11
3=。