第9章 振动学基础 习题答案

习题9-5.在气垫导轨上质量为m 的物体由两个轻弹簧分别固定在气垫导轨的两端，如图所示，试证明物体m 的左右运动为简谐振动，并求其振动周期。

设弹簧的劲度系数为k 1和k2.解：取物体在平衡位置为坐标原点，则物体在任意位置时受的力为 12()F k k x =-+ 根据牛顿第二定律有2122()d xF k k x ma m dt=-+==化简得21220k k d x x dt m++= 令212k k m ω+=则2220d x x dtω+=所以物体做简谐振动，其周期22T πω==9-6 如图所示在电场强度为E 的匀强电场中，放置一电偶极矩P=ql 的电偶极子，+q 和-q 相距l ，且l 不变。

若有一外界扰动使这对电荷偏过一微小角度，扰动消失后，这对电荷会以垂直与电场并通过l 的中心点o 的直线为轴来回摆动。

试证明这种摆动是近似的简谐振动，并求其振动周期。

设电荷的质量皆为m ，重力忽略不计。

解 取逆时针的力矩方向为正方向，当电偶极子在如图所示位置时，点偶极子所受力矩为 sin sin sin 22l lM qE qE qEl θθθ=--=- 点偶极子对中心O 点的转动惯量为2221222l l J m m ml ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭由转动定律知2221sin 2d M qEl J ml dtθθβ=-==∙化简得222sin 0d qEdt mlθθ+=当角度很小时有sin θθ≈，若令22qEmlω=，则上式变为222sin 0d dtθωθ+= 所以电偶极子的微小摆动是简谐振动。

而且其周期为22T πω==9-7 汽车的质量一般支承在固定与轴承的若干根弹簧上，成为一倒置的弹簧振子。

汽车为开动时，上下为自由振动的频率应保持在 1.3v Hz = 附近，与人的步行频率接近，才能使乘客没有不适之感。

问汽车正常载重时，每根弹簧松弛状态下压缩了多少长度？解 汽车正常载重时的质量为m ，振子总劲度系数为k ，则振动的周期为2T =，频率为1v T == 正常载重时弹簧的压缩量为22220.15()44mg T g x g m k vππ====9-8 一根质量为m ，长为l 的均匀细棒，一端悬挂在水平轴O 点，如图所示。

第9章振动学基础习题9.1 质量为10×10-3kg的小球与轻弹簧组成的系统，按x=0.1cos（8πt＋2π/3）（SI）的规律振动，求：（1）振动的圆频率、周期、振幅、初相以及速度与加速度的最大值；（2）最大回复力、振动能量、平均动能和平均势能；（3）t＝1、2、5、10s等各时刻的相位；（4）分别画出振动的x-t图线，v-t图线和a-t图线；（5）画出这些振动的转动矢量图示，并在图中指明t＝1、2、5、10s时矢量的位置。

9.2 一个弹簧振子m=0.5kg，k=50N／m，振幅A=0.04m，求：（1）振动的圆频率，最大速度和最大加速度；（2）当振子对平衡位置的位移为x=0.02m时的瞬时速度、加速度和回复力；（3）以速度具有正的最大值时为计时起点，写出振动的表达式。

9.3 一质点在x=0附近沿x轴作简谐振动。

在t=0时位置为x=0.37cm，速度为零，振动频率为0.25Hz。

试求：（1）周期、圆频率、振幅；（2）在时刻t的位置和速度；（3）最大速度和最大加速度的值；（4）在t=3.0s时的位置和速率。

9.4 作简谐振动的小球，速度最大值为v m=3cm/s，振幅A=2cm，若从速度为正的最大值时开始计算时间，求：（1）振动的周期；（2）加速度的最大值；（3）振动表达式。

9.5 如图，两轻弹簧与小球串联在一直线上，将两弹簧拉长后系在固定点A、B之间，整个系统放在水平面上。

设弹簧的原长为l1、l2，倔强系数为k1、k1，A、B间距离为L，小球的质量为m。

（1）试确定小球的平衡位置。

（2）使小球沿弹簧长度的方向作一微小位移后放手，小球将作振动，这一振动是否是简谐振动？振动的周期为多少？9.6 一轻弹簧的倔强系数为k，其下悬有一质量为m的盘子。

现有一质量为M的物体从离盘h高度处自由下落到盘中并和盘子粘在一起，盘子开始振动起来。

（1）此时振动周期与空盘振动的周期各为多少？（2）此时振动的振幅。

振动学基础练习题及答案一、选择1、物体做简谐运动时，下列叙述中正确的是 [ C ]（A ）在平衡位置加速度最大； （B ）在平衡位置速度最小； （C ）在运动路径两端加速度最大； （D ）在运动路径两端加速度最小。

2、作简谐运动的单摆，在最大角位移向平衡位置运动过程中 [ B ]（A ）动能减少，势能增加； (B) 动能增加，势能减少；（C ）动能增加，势能增加； (D) 动能减少，势能减少。

3、弹簧振子沿直线作简谐振动，当振子连续两次经过相同位置时，以下说法正确的是（A ）加速度不同，动能相同； [ C ] （B ）动能相同，动量相同； （C ）回复力相同，弹性势能相同； （D ）位移、速度和加速度都相同。

4、一弹簧振子，当0t =时，物体处在/2x A =（A 为振幅）处且向负方向运动，则它的初相为[ A ]（A ）π3； （B ）π6； （C ）-π3； （D ）-π6。

5、把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时。

若用余弦函数表示其运动方程，则该单摆振动的初相为 [ C ](A) π ； (B) π/2 ； (C) 0 ； (D) θ 。

6、一质点作简谐振动，周期为T 。

当它由平衡位置向x 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为 [ C ](A) T /12 ； (B) T /8 ； (C) T /6 ； (D) T /47、一质点沿x 轴作简谐振动，振动方程为 10.04cos(2)3x t ππ=+（SI ），从t = 0时刻起，到质点位置在x = -0.02 m 处，且向x 轴正方向运动的最短时间间隔为 [ D ](A)s 81； (B) s 61； (C) s 41； (D) s 21。

8、一弹簧振子，物体的质量为m ，弹簧的劲度系数为k ，该振子作振幅为A 的简谐振动。

当物体通过平衡位置且向规定的正方向运动时开始计时。

第九章一、选择题1、弹簧振子作简谐运动时，如果振幅增加为原来的两倍，则它的总能量是[ ](A) 原来总能量的2倍 (B) 原来总能量的4倍(C) 原来总能量的一半 (D) 不发生变化2、关于共振，下列说法正确的是：[ ](A) 当振子作无阻尼受迫振动时，共振时振幅为无限大(B) 当振子作无阻尼受迫振动时，共振的振幅很大，但不会无限大(C) 受迫振动是一个稳定的简谐振动(D) 共振不是受迫振动3、弹簧振子作简谐运动时，如果振幅增加为原来的两倍，而频率减小为原来的一半，则它的总能量是[ ]（A）原来总能量的2倍（B）原来总能量的4倍（C）原来总能量的一半（D）不发生变化4、对一个作简谐振动的物体，下面哪种说法是正确的？[ ](A) 物体处在运动正方向的端点时，速度和加速度都达到最大值(B) 物体位于平衡位置且向负方向运动时，速度和加速度都为零(C) 物体位于平衡位置且向正方向运动时，速度最大，加速度为零(D) 物体处在负方向的端点时，速度最大，加速度为零5、以下关于简谐振动的合成，说法正确的是[ ]（A）两个同方向、同频率简谐振动合成后还是一个简谐振动，频率发生了改变（B）两个同方向、同频率简谐振动合成后还是一个简谐振动，频率不发生改变（C）两个同方向、同频率简谐振动合成后不是一个简谐振动，频率不发生改变（D）两个同方向、同频率简谐振动合成后不是一个简谐振动，频率发生了改变6、以下关于驻波的说法错误的是[ ]（A）驻波是入射波和反射波叠加的结果（B）驻波中，除了节点外，各点均做同频率的简谐振动（C）驻波中，波腹和波节等距离交互排列（D ）两相邻波节间各点的振动位相相同，一波节两侧的点的振动位相也相同7、一质点同时参与两个同方向的简谐振动，振动方程分别为)45cos(05.01π+=t x ，250.05cos(5)4x t π=+，则合振动方程为[ ] (A) 0 (B) 30.05cos(5)2x t π=+ (C) 30.1cos(5)2x t π=+ (D)30.1cos(10)2x t π=+8、同一个弹簧振子，使它分别在光滑水平面上，竖直方向上，光滑的斜面上以相同的振幅作简谐振动，则：[ ]（A ）它们的频率不同 （B ）通过平衡位置时的动能不同（C ）到达平衡位置时弹簧形变相同 （D ）它们的周期相同9、竖直弹簧振子系统谐振周期为T ，将小球放入水中，水的浮力恒定，粘滞阻力及弹簧质量不计，若使振子沿铅直方向振动起来，则：[ ](A) 振子仍作简谐振动，但周期<T (B) 振子仍作简谐振动，但周期>T(C) 振子仍作简谐振动，且周期仍为T (D) 振子不再作简谐振动10、一质点的振动方程为：)3/2cos(2.0ππ+=t x ，则在t=0.3 （s ）时：[ ](A) 质点在平衡位置右方，沿x 轴负向运动(B) 质点在平衡位置左方，沿x 轴正向运动(C) 质点在平衡位置右方，沿x 轴正向运动(D) 质点在平衡位置左方，沿x 轴负向运动11、弹簧振子作简谐振动时的总能量为E ，如果振幅增大为原来的两倍，振动质量减少为原来的一半，则总能量E’为：[ ]（A ）E’=E （B ）E’=2E （C ）E’=0.5E （D ）E’=4E12、质量为m 的物体作简谐振动，振幅为A ，最大加速度为a ，则通过平衡位置时的动能为：[ ]（A ）0.5maA 2 (B) 0.5ma 2A 2 (C) ma 2A 2 (D) 0.5maA二、填空题1、两个同方向同频率的简谐振动合成后的运动是 。

第9章 振动学基础 复习题1.已知质点的振动方程为)cos(ϕω+=t A x ，当时间4Tt =时 (T 为周期)，质点的振动速度为:（A ）ϕωsin A v -= （B ）ϕωsin A v =（C ）ϕωcos A v = （D ）ϕωcos A v -=2．两个分振动的位相差为2π时，合振动的振幅是：A.A 1+A 2;B.| A 1-A 2|C.在.A 1+A 2和| A 1-A 2|之间D.无法确定3．一个做简谐运动的物体，在水平方向运动，振幅为8cm ，周期为0.50s 。

t =0时，物体位于离平衡位置4cm 处向正方向运动，则简谐运动方程为 . 4.一质点沿x 轴作简谐振动，振动方程为 )32cos(1042ππ+⨯=-t x m 。

从t = 0时刻起，到质点位置在x = -2 cm 处，且向x 轴正方向运动的最短时间间隔为 .5．一个简谐振动在t=0时位于离平衡位置6cm 处，速度v =0，振动的周期为2s ，则简谐振动的振动方程为 .6.一质点作谐振动，周期为T ，当它由平衡位置向 x 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为 .7.一个质量为0.20kg 的物体作简谐振动，其振动方程为)25cos(6.0π-=t x m ，当振动动能和势能相等时振动物体的位置在A ．3.0±mB ．35.0± mC ．42.0±mD ．0 8．某质点参与)43cos(41ππ+=t x cm 和)43cos(32ππ-=t x cm 两个同方向振动的简谐振动，其合振动的振幅为 9. 某质点参与)22cos(101ππ+=t x cm 和)22cos(41ππ-=t x cm 两个同方向振动的简谐运动，其合振动的振幅为 ;10．一个作简谐振动的物体的振动方程为cm t s )3cos(12ππ-=,当此物体由cm s 12-=处回到平衡位置所需要的最短时间为 。

第9章 振动学基础答案9.4 一个运动质点的位置与时间的关系为 m t x ⎪⎭⎫ ⎝⎛+=325cos 1.0ππ , 其中x 的单位是m , t 的单位是s .试求：（1）周期、角频率、频率、振幅和初相位； （2）t =2s 时质点的位移、速度和加速度.解：（1）由题中质点位置与时间的关系便知，振幅A =0.1m ，初相位3πϕ=，角频率s rad /25πω=，频率Hz 45=ν，周期s f T 8.0541===（2）⎪⎭⎫ ⎝⎛+-==325sin 41πππυt dt dx ；⎪⎭⎫ ⎝⎛+-==325cos 85222πππt dt x d a 则当t=2s 时，质点的位移，速度和加速度分别为m x 05.03cos 1.03225cos 1.0-=-=⎪⎭⎫ ⎝⎛+⨯=πππ；s m /68.0833sin 413225sin 41===⎪⎭⎫ ⎝⎛+⨯-=ππππππυ222/1.33cos 853225cos 85s m a ==⎪⎭⎫ ⎝⎛+⨯-=πππππ9.5 一个质量为2.5kg 的物体，系于水平放置的轻弹簧的一端，弹簧的另一端被固定.若弹簧受10N 的拉力,其伸长量为5.0cm,求物体的振动周期.解：由kx f =可得弹簧的经度系数为 m N x f k /1021051022⨯=⨯==- 弹簧振子的周期 s k m T 70.01025.2222=⨯==ππ9.6 如图9.27图所示 ,求振动装置的振动频率,已知物体的质量为m ,两个轻弹簧的劲度系数为1k 和2k 。

解：设物体离开平衡位置的位移是x ，此时物体所受合力x k k f )(21+-=作为线性回复力，则有021=++x m k k x故m k k 21+=ω mk k 2121+=πν9.7 如图9.28所示 , 求振动装置的振动频率,已知物体的质量为m ,两个轻弹簧的径度系数为1k 和2k 。

解：设物体m 离开平衡位置的位移为x ，所受线性回复力为f 则有）（12211x k x k f -=-= )2(21xx x =+（1）、（2）联立解之得 212121/1/11k k k k x k k f +-=+-=所以有振动方程0)(12121=++x k k k k m x，则 )(21,)(21212121k k m k k k k m k k +=+=πνω9.8 仿照式（9.15）的推导过程,导出在单摆系统中物体的速度与角位移的关系式.解：对于单摆系统中的物体m ，其振动动能 2222121θυ ml m E k == 系统的势能（重力势能）221)cos 1(θθmgl mgl mgh E p ≈-== 而系统的总能量 201θm gl E E E p k =+= 所以20212212221θθθmglmglml =+ 由此得：)()(22022202θθωθθθ-=-=lg )220θθωθ-±= 9.9 与轻弹簧的一端相接的小球沿x 轴作简谐振动,振幅为A ,位移与时间的关系可以用余弦函数表示.若在t =0时,小球的运动状态分别为（1）x = - A ；（2）过平衡位置,向x 轴正向运动；（3）过x =A /2处,向x 轴负向运动；（4）过2/A x =处,向x 轴正向运动.试确定上述状态的初相位. 解：位移x 与时间t 的一般关系可表为 )cos(ϕω+=t A x（1）t =0时，A x -=， 则有ϕcos A A =-， 即1cos -=ϕ。

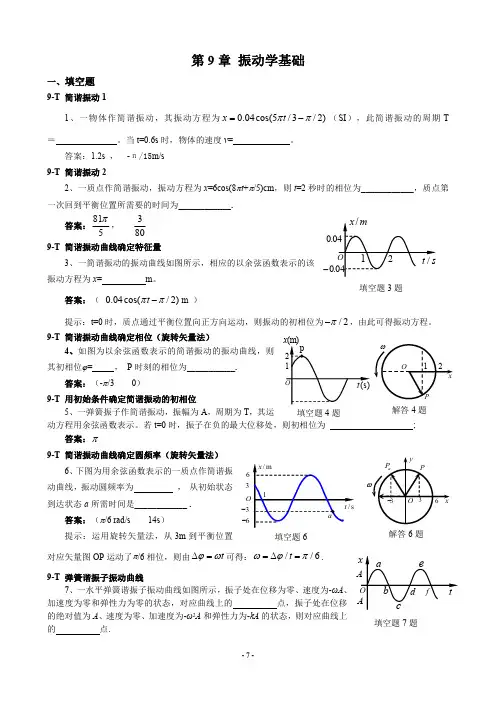
第九章 振动学习题9-1 一小球与轻弹簧组成的振动系统，按(m) 3ππ8cos 05.0⎪⎭⎫ ⎝⎛+=t x ，的规律做自由振动，试求（1）振动的角频率、周期、振幅、初相、速度最大值和加速度最大值；（2）t=1s ，2s ，10s 等时刻的相位；（3）分别画出位移、速度和加速度随时间变化的关系曲线。

解：（1）ω=8πs -1，T=2π/ω=0.25s ，A=0.05m ，ϕ0=π/3，m A ω=v ，2m a A ω=（2）π=8π3t φ+ （3）略9-2 一远洋货轮质量为m ，浮在水面时其水平截面积为S 。

设在水面附近货轮的水平截面积近似相等，水的密度为ρ，且不计水的粘滞阻力。

（1）证明货轮在水中做振幅较小的竖直自由运动是谐振动；（2）求振动周期。

解：（1）船处于静止状态时gSh mg ρ=，船振动的一瞬间()F gS h y mg ρ=-++ 得F gSy ρ=-，令k gS ρ=，即F ky =-，货轮竖直自由运动是谐振动。

（2）ω==，2π2T ω==9-3 设地球是一个密度为ρ的均匀球体。

现假定沿直径凿通一条隧道，一质点在隧道内做无摩擦运动。

（1）证明此质点的运动是谐振动；（2）计算其振动周期。

解：以球心为原点建立坐标轴Ox 。

质点距球心x 时所受力为324433x mF G G mx x πρπρ=-=-令43k G m πρ=，则有F kx =-，即质点做谐振动。

（2）ω==2πT ω== 9-4 一放置在水平桌面上的弹簧振子，振幅A ＝2.0 ×10-2 m ，周期T s 。

当t ＝0时，（1）物体在正方向端点；（2）物体在平衡位置，向负方向运动；（3）物体在x ×10-2m 处，向负方向运动；（4）物体在x ＝-×10-2 m 处，向正方向运动。

求以上各种情况的振动方程。

解：ω=2π/T=4πs -1（1）ϕ0=0，0.02cos4(m)x t π=（2）ϕ0=π/2，0.02cos 4(m)2x t ππ⎛⎫=+ ⎪⎝⎭（3）ϕ0=π/3，0.02cos 4(m)3x t ππ⎛⎫=+ ⎪⎝⎭（4）ϕ0=4π/3，40.02cos 4(m)3x t ππ⎛⎫=+ ⎪⎝⎭9-5 有一弹簧，当其下端挂一质量为m 的物体时，伸长量为9.8 ×10-2 m 。