振动、波动学基础选择题及参考答案

大学物理1复习题答案一、单选题(在本题的每一小题备选答案中，只有一个答案是正确的,请把你认为正确答案的题号，填入题干的括号内)1．一个弹簧振子和一个单摆（只考虑小幅度摆动)，在地面上的固有振动周期分别为T 1和T 2。

将它们拿到月球上去，相应的周期分别为'T 1和'T 2。

则有 （ B ）A ．'T T >11且 'T T >22B ．'T T =11且 'T T >22C ．'T T <11且 'T T <22D ．'T T =11且 'T T =222．一物体作简谐振动，振动方程为cos 4x A t ⎛⎫=+⎪⎝⎭πω,在4Tt =(T 为周期）时刻，物体的加速度为 （ B )A. 2ω B 。

2ω C 。

2ω D2ω3．一质点作简谐振动,振幅为A ，在起始时刻质点的位移为/2A -，且向x 轴的正方向 运动,代表此简谐振动的旋转矢量图为 （ D )AAAAAAC)AxxAAxA B C D4。

两个质点各自作简谐振动，它们的振幅相同、周期相同．第一个质点的振动方程为)cos(1αω+=t A x ．当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处．则第二个质点的振动方程为 （ B )A. )π21cos(2++=αωt A x B. )π21cos(2-+=αωt A x ． C 。

)π23cos(2-+=αωt A x D. )cos(2π++=αωt A x ． 5．波源作简谐运动,其运动方程为t y π240cos 100.43-⨯=,式中y 的单位为m ，t 的单位为s ，它所形成的波形以s m /30的速度沿一直线传播，则该波的波长为 （ A ）A ．m 25.0B ．m 60.0C ．m 50.0D ．m 32.06．已知某简谐振动的振动曲线如图所示，位移的单位为厘米，时间单位为秒.则此简谐振动的振动方程为: （ B ）A ．cos x t ππ⎛⎫=+ ⎪⎝⎭22233B ．cos x t ππ⎛⎫=+ ⎪⎝⎭42233C ．cos x t ππ⎛⎫=- ⎪⎝⎭22233D ．cos x t ππ⎛⎫=- ⎪⎝⎭42233二． 填空题（每空2分）1． 简谐运动方程为)420cos(1.0ππ+=t y （t 以s 计,y 以m 计），则其振幅为 0.1 m ，周期为 0。

06振动与波、波动光学练习题 一、选择题 1 一物体作简谐振动，振动方程为)4cos(πω+=t A y在4T t =（T 为周期）时刻，物体的加速度为 [ ]2222321)(,321)(,221)(,221)(ωωωωA D A C A B A A -- 2 两个质点各自作简谐振动，它们的振幅相同、周期相同，第一个质点的振动方程为)cos(1αω+=t A y 。

当第一个质点从相对平衡位置的正位移处回到平衡位置时，第二个质点正在最大位移处，则第二个质点的振动方程为 [ ])cos()(),23cos()()2cos()(),2cos()(2222παωπαωπαωπαω++=-+=-+=++=t A y D t A y C t A y B t A y A 3一质点沿y 轴作简谐振动，振动方程为)SI (),32cos(1042παπ++⨯=-t y ，从t = 0时刻起，到质点位置在x = －2 cm 处，且向x 轴正方向运动的最短时间间隔为[ ]s 61)(s,31)(s,21)(s,41)(s,81)(E D C B A 4 已知两个简谐振动曲线如图所示，1x 相位比2x 的相位 [ ]ππππ超前，落后，超前，落后)()(2)(2)(D C B A5题图 7题图5 一质点作简谐振动，周期为T 。

质点由平衡位置向X 轴正方向运动时，由平衡位置到二分之一最大位移这段路程所需要的时间为 [ ],8)(6)(12)(4)(T D T C T B T A ，，， 6 在下面几种说法中，正确的说法是： [ ]（A ）波源不动时，波源的振动周期与波动的周期在数值上是不同的，（B ）波源振动的速度与波速相同，(C) 在波传播方向上的任一质点的振动相位总是比波源的相位滞后，(D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前。

7一平面简谐波，沿X 轴负方向传播，角频率为ω，波速为u 。

设4T t =时刻的波形如图所示，则该波的表达式为： [ ]])(cos[)(),(cos )(]21)(cos[)(),(cos )(πωωπωω++=+=+-=-=ux t A y D u x t A y G u x t A y B ux t A y A 8 当机械波在媒质中传播时，一媒质质元的最大变形量发生在 [ ](A)媒质质元离开其平衡位置最大位移处，（B ）媒质质元离开其平衡位置)2/2(A 处，（C ）媒质质元在其平衡位置处，（D ）媒质质元离开其平衡位置A/2处(A 是振动振幅)。

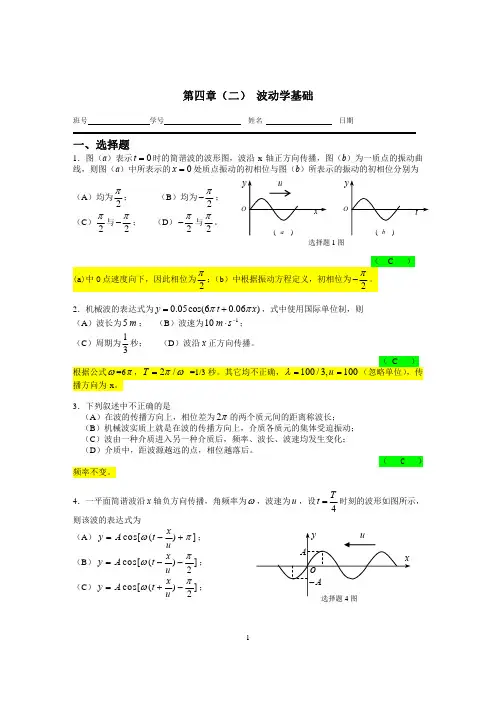
振 动一、填空题： 1、21T ； 2、;10cm A =16-⋅=srad πω；3πϕ=； 3、gl 322π4、（略）； 二、计算题： 1、 解：是；假设木块的边长为L ，平衡时浸入水中的高度为h ， 平衡时: h gl F mg 2水浮＝ρ=在任一位置时：x l l x h h gl F mg F g )(g 222水水水浮＝ρρρ-=+-'-=∑ 令 K ＝g 2水ρl则∑Kx F ＝－，K 是一个常数，表明木块所作的运动是简谐振动。

由∑=22dtx d m F ，可得木块运动的微分方程为：22dtx d ＋0/2=m x gl 水ρ令m l /g 22水ρω=，可得其振动周期为：2/22l g m T 水ρπωπ==2、解：（1）要求物体的简谐运动方程，要确定角频率、振幅和初相：110.602.072.0--=⋅==skg m N mk ω再根据2202ωv x A +=由于0,05.000==v m x ，故m x v x A 05.0022020==+=ω初相：00=-=x v tg ωϕ，πϕ或0=，根据已知条件：0=ϕ则简谐振动的方程为：])0.6cos[()05.0(1t s m x -= （2）物体第一次抵达2A 处时，即t A ωcos 2=，故353ππω或=t ，用旋转矢量法，得3t πω=，故：126.0sin -⋅-=-=s m t A v ωω3、解： （1）由题意，假设简谐振动的表达式：)cos(ϕω+=t A x 得速度的表达式：)sin(ϕω+-=wt A v 故：ωA v m ==2103-⨯故：5.110210322=⨯⨯==--Av m ω（2）由速度的表达式可得加速度的表达式为：)cos(2ϕωω+-=t A a则：2ωA a m ==2222/105.45.1102s m --⨯=⨯⨯ （3）振动的表达式为：)25.1cos(1022π-⨯=-t x4、解： 如图所示，可得两个分振动分别为：)2cos(08.01ππ-=t x )2cos(04.02ππ+=t x故：合振动的方程为：)2cos(04.021ππ-=+=t x x x5、解：由旋转矢量法解。

振动、波动练习题及答案振动、波动练习题⼀．选择题1．⼀质点在X 轴上作简谐振动，振幅A=4cm。

周期T=2s。

其平衡位置取作坐标原点。

若t=0 时刻质点第⼀次通过x= -2cm 处，且向X 轴负⽅向运动，则质点第⼆次通过x= -2cm 处的时刻为（）。

A 1sB 2sC 4sD 2s332．⼀圆频率为ω的简谐波沿X 轴的正⽅向传播，t=0 时刻的波形如图所⽰，则t=0 的波形t=0 时刻，X 轴上各点的振动速度υ与X轴上坐标的关系图应（）3．图⽰⼀简谐波在 t=0 时刻的波形图，波速υ =200m/s ，则图中O 点的振动加速度的表达式为（）2A a 0.4 2 cos( t ) 2 23B a 0.4 2 cos( t )22C a 0.4 2cos(2 t ) 4．频率为 100Hz ，传播速度为 300m/s 的平⾯简谐波，波线上两点振动的相位差为 3 ，则这两点相距（）A 2mB 2.19mC 0.5mD 28.6m5．⼀平⾯简谐波在弹性媒质中传播，媒质质元从平衡位置运动到最⼤位置处的过程中，（）。

A 它的动能转换成势能它的势能转换成动C 它从相邻的⼀段质元获得能量其能量逐渐增⼤Da20.4 2 cos(2 t2)υ (m/s)Bυ (m/s)DX(m)D 它把⾃⼰的能量传给相邻的⼀段质元，其能量逐渐减⼩6．在下⾯⼏种说法中，正确的说法是：（）。

A 波源不动时，波源的振动周期与波动的周期在数值上是不同的B 波源振动的速度与波速相同C 在波传播⽅向上的任⼀质点振动位相总是⽐波源的位相滞后D 在波传播⽅向上的任⼀质点振动位相总是⽐波源的位相超前7．⼀质点作简谐振动，周期为T，当它由平衡位置向X 轴正⽅向运动时，从⼆分之⼀最⼤位移处到最⼤位移处这段路程所需要的时间为（）。

A TBTCTDT4 12 6 88．在波长为λ的驻波中两个相邻波节之间的距离为（）。

A λB 3 λ/4C λ/2D λ /49．在同⼀媒质中两列相⼲的平⾯简谐波的强度之⽐I1I 4是，则两列波的振幅之⽐是：（）A A1 4 B1 2 CA1 16 DA11A2 A2 A2 A2 410．有⼆个弹簧振⼦系统，都在作振幅相同的简谐振动，⼆个轻质弹簧的劲度系数K 相同，但振⼦的质量不同。

大学物理学——振动和波振 动班级 学号 姓名 成绩内容提要1、简谐振动的三个判据（1）；（2）；（3）2、描述简谐振动的特征量： A 、T 、γ；T1=γ，πγπω22==T3、简谐振动的描述：（1）公式法 ；（2）图像法；（3）旋转矢量法4、简谐振动的速度和加速度：)2cos()sin(v00πϕωϕωω++=+-==t v t A dt dx m ； a=）（）（πϕωϕωω±+=+=0m 0222t a t cos -dtxd A 5、振动的相位随时间变化的关系：6、简谐振动实例弹簧振子：，单摆小角度振动：，复摆：0mgh dt d 22=+θθJ ,T=2mghJπ 7、简谐振动的能量：222m 21k 21A A Eω==系统的动能为：）（ϕωω+==t sin m 21mv 212222A E K ；系统的势能为：）ϕω+==t (cos k 21kx 21222A E P8、两个简谐振动的合成（1）两个同方向同频率的简谐振动的合成合振动方程为：）（ϕω+=t cos x A其中，其中；。

＊(2) 两个同方向不同频率简谐振动的合成拍：当频率较大而频率之差很小的两个同方向简谐运动合成时，其合振动的振幅表现为时而加强时而减弱的现象，拍频：12-γγγ=＊（3）两个相互垂直简谐振动的合成合振动方程：）（1221221222212-sin )(cos xy 2y x ϕϕϕϕ=--+A A A A ，为椭圆方程。

练习一一、 填空题1．一劲度系数为k 的轻弹簧，下端挂一质量为m 的物体，系统的振动周期为T 1。

若将此弹簧截去一半的长度，下端挂一质量为m/2的物体，则系统的周期T 2等于 。

2．一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为：A ＝ ；=ω ;=ϕ 。

3．如图，一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上，做成一复摆。

已知细棒绕过其一端的轴的转动惯量J ＝3/2ml ，此摆作微小振动的周期为 。

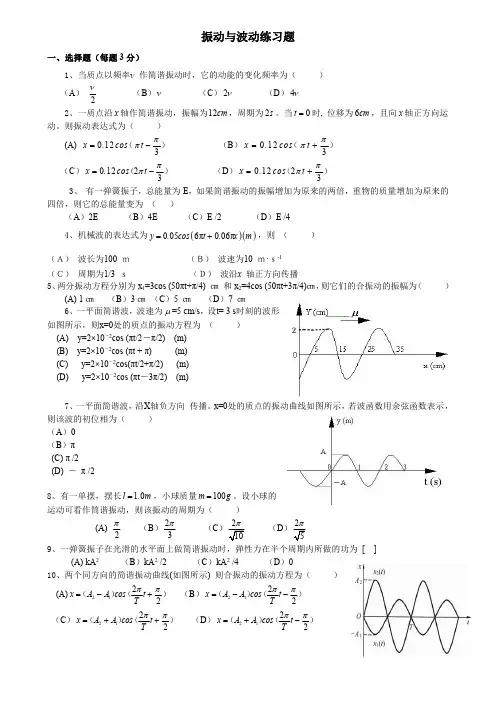
振动和波一、选择题1.（3分,答D ）已知一平面简谐波的表达式为cos()y A at bx =-（,a b 为正值常量），则 （A ）波的频率为a （B ）波的传播速度为/b a （C ）波长为/b π （D ）波的周期为2/a π2.（本题3分，答B ）一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为A 21，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为［］3. （3分,答B ）一质点在x 轴上作简谐振动，振幅A =4cm ，周期T =2s ，其平衡位置取作坐标原点，若t =0时刻质点第一次通过x =-2cm 处，且向x 轴负方向运动，则质点第二次通过x =-2cm 处的时刻为(A) 1s (B) (2/3)s (C)(4/3)s (D) 2s4. （3分,答D ）一劲度系数为k 的轻弹簧，下端挂一质量为m 的物体，系统的振动周期为T 1．若将此弹簧截去一半的长度，下端挂一质量为m 21的物体，则系统振动周期T 2等于 (A) 2 T 1 (B) T 1(C)T 12/ (D) T 1 /2 (E) T 1 /45.（本题3分，答A ）轴一简谐波沿Ox 轴正方向传播，t = 0 时刻的波形曲线如图所示，已知周期为 2 s ，则 P 点处质点的振动速度v 与时间t 的关系曲线为：6.（3分，答B ）一平面简谐波在弹性媒质时，某一时刻媒质中某质元在负最大位移处，则它的能量是（A ） 动能为零 势能最大 （B ）动能为零 势能为零 （C ） 动能最大 势能最大 （D ）动能最大 势能为零v (m/s)O 1 t (s)ωA(C)· v (m/s)O1 t (s)ω A(A)·1 v (m/s)t (s)(D)O－ω A1 v (m/s) t (s)－ωA(B) O ··x o A x A 21 ω(A)A 21ω(B) A 21-(C) (D)o oo A 21-xxxAxAxAxω ω2O 1 y (m)x (m)t =0 A u图17.（3分，答D ）沿相反方向传播的两列相干波，其波动方程为y 1=A cos2π (νt －x /λ)y 2=A cos2π (νt + x /λ) 叠加后形成的驻波中,波节的位置坐标为(A)x =±k λ.(B)x =±k λ/2 .(C)x =±(2k +1)λ/2 .(D)x =±(2k +1)λ/4 . 其中k = 0 , 1 , 2 , 3…….8.（3分,答D ）如图所示，有一平面简谐波沿x 轴负方向传播，坐标原点O 的振动规律为y =A cos(ω t+φ0)，则B 点的振动方程为 （A ）y =A cos[ω t-(x/u )+φ0] （B ）y =A cos ω[ t+(x/u )] （C ）y =A cos{ω [t-(x/u ) ]+φ0} （D ）y =A cos{ω[ t+(x/u ) ]+φ0}9.（3分,答D ）一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到最大位移处的过程中：（A ）它的动能转换成势能. （B ）它的势能转换成动能. （C ）它从相邻的一段质元获得能量，其能量逐渐增大. （D ）它把自己的能量传给相邻的一段质元，其能量逐渐减小. 10.（3分，答B ）在波长为λ的驻波中，两个相邻波腹之间的距离为 （A ）λ/4 （B ）λ/2 （C ）3λ/4 （D ）λ11.（3分,答C ）某时刻驻波波形曲线如图所示，则a 、b 两点振动的相位差是 （A ）0 （B ）/2π （C ）π （D ）5/4π12.（本题3分，答B)在驻波中，两个相邻波节间各质点的振动（A ）振幅相同，相位相同 （B ）振幅不同，相位相同 （C ）振幅相同，相位不同 （D ）振幅不同，相位不同 二、填空题1. （3分）已知一个简谐振动的振幅A=2cm, 角频率14s ωπ-=，以余弦函数表达式运动规律时的A －Ayxλ λ/2O ··a b · · · · · · · · ··x 2A A/2x 1初相12φπ=，试画出位移和时间的关系曲线（振动图线） 2.（4分）两个简谐振动方程分别为x 1=Acos(ω t ) ；x 2=Acos(ω t +π/3) 在同一坐标上画出两者的x-t 曲线.3. (3分）有两相同的弹簧，其劲度系数均为k .（1）把它们串联起来，下面挂一个质量为m 的重物，此系统作简谐振动的周期为；（2）把它们并联起来，下面挂一个质量为m 的重物，此系统作简谐振动的周期为.[答案：（1）22m k π,（2）22mkπ] 4.(4分)一弹簧振子系统具有1.0J 的振动能量，0.10m 的振幅和1.0m/s 的最大速率，则弹簧的劲度系数，振子的振动频率.[答案：2210N/m,1.6Hz ⨯]5.（3分）一平面机械波沿x =-1m 轴负方向传播，已知处质点的振动方程cos()y A t ωϕ=+，若波速为u ，求此波的波函数.[答案：cos{[(1)/]}y A t x u ωϕ=+++]6.（3分）一作简谐振动的振动系统，振子质量为2kg ，系统振动频率为1000Hz ，振幅为0.5cm ，则其振动能量为.（答案：29.9010J ⨯ ）7.（3分）两个同方向同频率的简谐振动211310cos(),3x t ωπ-=⨯+221410cos()(SI)6x t ωπ-=⨯-，它们的合振幅是. （答案：2510m -⨯ ）8.（3分）一平面简谐波沿Ox 轴正方向传播，波动表达式为cos[(/)/4]y A t x u ωπ=-+，则1x L =处质点的振动方程是；2x L =-处质点的振动和1x L =处质点的振动相位差为21φφ-=. （答案：1cos[(/)/4]y A t L u ωπ=-+，12()/L L u ω+）9.（5分）一余弦横波以速度u 沿x 轴正向传播，t 时刻波形曲线如图所示.试分别指出图中A ，B ，C 各质点在该时刻的运动方向.A 向下 ，B 向上 ，C 向上.10. （本题4分）一平面简谐波的表达式cos (/)cos(/)y A t x u A t x u ωωω=-=-其中/x u 表示，/x u ω表示，y 表示.[答案：波从坐标原点传至x 处所需时间（2分），x 处质点此原点处质点滞后的相位（1分），t 时刻x 处质点的振动位移（1分）]11. （本题3分）如图所示，两相干波源S 1和S 2相距为3λ/4，λ为波长，设两波在S 1 S 2连O Cyxu · · · A B线上传播，它们的振幅都是A ，并且不随距离变化，已知在该直线上S 1左侧各点的合成波强度为其中一个波强度的4倍，则两波源应满足的相位条件是__π/2_ 12. （3分）一驻波的表达式为y =2A cos(2πx/λ) cos(2πνt )，两个相邻波 腹之间的距离是.（答案：λ/2） 三、计算题1. （5分）一质点作简谐运动，其振动方程为110.24cos()()23x t SI ππ=+，试用旋转矢量法求出质点由初始状态运动到x =-0.12 m ，v <0的状态所经过的最短时间． 解：旋转矢量如图所示．图3分 由振动方程可得π21=ω，π=∆31φ1分667.0/=∆=∆ωφt s 1分2（本题10分）一质量m =0.25kg 的物体，在弹簧的力作用下沿x 轴运动，平衡位置在原点，弹簧的劲度系数k =25N/m.（1）求振动的周期T 和频率ω. （2）如果振幅A =15cm ，t =0时物体位于x =7.5cm 处，且物体沿x 轴反方向运动，求初速度v 0及初相φ.（3）写出振动的数值表达式. 解：（1）12/10k m s ωπ-== (2分)2/0.63T s πω== (1分)(2) A=15cm ， 在t =0时，07.5cm x =，00v < 由2200(/)A x v ω=+得2200 1.3m/s v A x ω=--=- (2分)100(/)/3/3tg v x φωππ-=-=或400,/3x φπ>∴=(3分)（3）21510cos(10/3)(SI)x t π-=⨯+(2分)3.（10分）在一轻弹簧下端悬挂0100g m =砝码时，弹簧伸长8cm. 现在这根弹簧下端悬挂0250g m =物体，构成弹簧振子，将物体从平衡位置向下拉动4cm ，并给以向上的21cm/s 的初速度（令这时t=0）.选x 轴向下，求振动方程的数值式.解：k = m 0g / ∆l 25.12N/m 08.08.91.0=⨯=N/mx (m) ωωπ/3π/3t = 0t0.12 0.24 -0.12 -0.24 OAAO xS 1S 211s 7s 25.025.12/--===m k ω(2分) 5cm )721(4/2222020=+=+=ωv x A cm (2分) 4/3)74/()21()/(tg 00=⨯--=-=ωφx v ，φ = 0.64 rad (3分))64.07cos(05.0+=t x (SI) (1分)4．（8分）在一竖直轻弹簧的下端悬挂一小球，弹簧被拉长0 1.2cm l =而平衡.再经拉动后，该小球在竖直方向作振幅为2cm A =的振动，试证此振动为简谐振动；选小球在正最大位移处开始计时，写出此振动的数值表达式.解：设小球的质量为m ，则弹簧的劲度系数（图参考上题）0/k mg l = 选平衡位置为原点，向下为正方向. 小球在x 处时，根据牛顿第二定律得202()d x mg k l x m dt -+=将k 代入整理后得 220d x g x dt l =-所以振动为简谐振动，其角频率为0/28.589.1(rad/s)g l ωπ===(5分)设振动表达式为 c o s ()x A t ωφ=+ 由题意：t=0时，200210m0x A v -==⨯=解得：0φ=2210cos(9.1)x t π-∴=⨯m (3分)5.(10分)在一轻弹簧下端悬挂m 0=100g 的砝码时,弹簧伸长8cm,现在这根弹簧下端悬挂m =250g 的物体, 构成弹簧振子. 将物体从平衡位置向下拉动4cm,并给以向上的21cm/s 的初速度(这时t =0) ，选x 轴向下，求振动方程的数值式. 解：物体受向下的重力和向上的弹性力.k=m 0g/∆l , x 0=4×10-2m, v 0=-21×10-2m/sω=()m l g m m k Δ0==7s -1A=22020ω/v x +=5×10-2m因A cos ϕ=4×10-2m, A sin ϕ=-v 0/ω=3×10-2m,有 ϕ=0.64rad 所以x=5×10-2cos(7t +0.64) (SI)6.（本题5分）一质量为0.2kg 的质点作简谐振动，其振动方程为10.6cos(5)(SI)2x t π=-求：（1）质点的初速度；（2）质点在正向最大位移一半处所受的力.解：（1）003.0sin(5)()0, 3.0m/s 2dx v t SI t v dt π==--==（2分） （2）2F ma m x ==-ω12x A =时， 1.5N F =-（无负号扣1分） （3分） 7.（5分）一平面简谐波沿x 轴正方向传播，波速为1m/s ，在x 轴上某质点的振动频率为1Hz ，振幅为0.01m. t = 0时该质点恰好在正最大位移处，若以该质点的平衡位置为x 轴的原点. 求此一维简谐波的表达式.解. 0.01cos[2()](m)y t x =-π8.（本题10分）某质点作简谐振动，周期为2s ，振幅为0.06m ，t =0时刻，质点恰好处在负最大位移处，求（1）该质点的振动方程.（2）此振动以波速u =2m/s 沿x 轴正方向传播时，形成的一维简谐波的波动表达式，（以该质点的平衡位置为坐标原点）；（3）该波的波长. 解：（1）振动方程 00.06cos(2/2)0.06cos()(SI)y t t ππππ=+=+3分 （2）0.06cos[((/))0.06cos[(/2))(SI)y t x u t x ππππ=-+=-+ 4分（3）波长4m uT λ==9.（10分）一列平面简谐波在以波速5m/s u =，沿x 轴正向传播，原点O 处质点的振动曲线如图所示.1）求解并画出25cm x =处质元的振动曲线 2）求解并画出3s t =时的波形曲线 解：1）原点O 处质元的振动方程为211210cos(),(SI)22y t ππ-=⨯-(2分)波的表达式 (2分)211210cos((/5)),(SI)22y t x ππ-=⨯--x =25m 处质元的振动方程21210cos(3),(SI)2y t ππ-=⨯-振动曲线如右y-t 图 (2分)2）t=3s 时的波形曲线方程2210cos(/10),(SI)y x ππ-=⨯-(2分)波形曲线见右y-x 图 (2分)10.（10分）某质点作简谐振动，周期为2s ，振幅为0.6m ，t =0时刻，质点恰好处在负最大4O2 y(cm)t (s)2位移处，求（1）该质点的振动方程；（2）此振动以波速u =2m/s 沿x 轴正方向传播时，形成的一维简谐波的波动表达式，（以该质点的平衡位置为坐标原点）；（3）该波的波长.解：(1) 振动方程)22cos(06.00π+π=ty )cos(06.0π+π=t (SI) (3分) (2) 波动表达式])/(cos[06.0π+-π=u x t y (4分)])21(cos[06.0π+-π=x t (SI)(3) 波长4==uT λm (3分)11.（5分）如图所示，一简谐波向x 轴正向传播，波速0500/,1,u m s x m P ==点的振动方程为10.03cos(500)(SI)2y t ππ=-. （1） 按图所示坐标系，写出相应的波的表达式； （2） 在图上画出t=0时刻的波形曲线.解：(1) 2m )250/500(/===νλu m 波的表达式 ]/2)1(21500cos[03.0),(λπ--π-π=x t t x y110.03cos[500(1)2/2]0.03cos(500)(SI)22t x t x =π-π--π=π+π-π(3分)(2) t = 0时刻的波形曲线x x x y π=π-π=sin 03.0)21cos(03.0)0,( (SI) (2分)12.（10分）图示一平面余弦波在t = 0 时刻与t = 2 s 时刻的波形图(波向左传播)．已知波速为u ，波的周期大于2 s ，求(1) 坐标原点处介质质点的振动方程；(2) 该波的波动表达式． 解：(1) 比较t = 0 时刻波形图与t = 2 s 时刻波形图，可知此波向左传播．在t = 0时刻，O 处质点φcos 0A =，φωsin 00A -=<v ，故2πφ-= 又t = 2 s ，O 处质点位移为)24cos(2/ππ-=νA A 所以244πππ-=-ν，ν = 1/16 Hz 振动方程为)28/cos(0ππ-=t A y (SI)(2) 波速u = 20 /2 m/s = 10 m/s,波长λ = u /ν = 160 m 波动表达式]21)16016(2cos[π-+π=x t A y (SI) x (m)uP y (m)O-2-112-0.030.03x (m)O160A y (m)8020t =0t =2 s2A。

物体的振动和波动练习题一、选择题1. 下列哪个不属于机械振动的基本特征？A. 振幅B. 周期C. 频率D. 波长2. 以下哪种波不需要介质传播？A. 机械波B. 横波C. 纵波D. 都需要介质传播3. 以下哪个现象不属于机械波传播中的失能?A. 反射B. 折射C. 干涉D. 散射4. 把频率为30Hz的振动用电路方式表示，需要设备的最小档位是A. 10sB. 1sC. 1msD. 1us5. 振幅越大，波的能量传播速度越快，这一说法A. 对B. 错6. 当一个横波传播时，传播介质上的每一个质点的振动方向A. 垂直于波的传播方向B. 与波的传播方向相同C. 与波的传播方向相反D. 与波的振动方向相同7. 下列不属于机械波的是A. 音波B. 光波C. 水波D. 地震波8. 声音能传播的介质是A. 真空B. 水C. 铁D. 木头9. 长度为0.1m的弦上传播的频率为500Hz的波，其波长为A. 10cmB. 20cmC. 40cmD. 50cm10. 一个在弹簧中传播的波，它所具有的振动特点可以用频率 f 表示。

当频率 f 增大时，振动速度将A. 不变B. 增大C. 减小D. 变为零二、填空题1. 机械波在介质中的传播速度与_________、_________有关。

2. 波长和_________成反比。

3. 波的频率和振动的_________有关。

4. 当光束从水中垂直射入空气时，光的_________发生折射。

5. 在两根相互平行的弹簧上各拧一节，右手拇指指向电流的方向，右手四指的弯曲方向表示_________。

三、简答题1. 请简要说明机械波和电磁波的区别。

2. 请解释频率和周期的概念，并写出它们的单位。

3. 什么是衰减? 请说明衰减对波传播的影响。

4. 什么是驻波? 它是如何形成的？5. 请举例说明机械波的反射和折射现象。

四、计算题1. 一支弦上传播的横波的振动频率为100Hz，波长为0.5m。

高中物理波动学试题及答案一、选择题（每题2分，共10分）1. 波的传播速度与介质的密度和弹性模量有关，以下哪个选项是错误的？A. 波速与介质密度成反比B. 波速与介质弹性模量成正比C. 波速与介质的密度成正比D. 波速与介质的弹性模量成反比2. 在同一均匀介质中，以下哪种波的传播速度最快？A. 横波B. 纵波C. 表面波D. 体波3. 以下哪个现象不属于机械波？A. 声波B. 电磁波C. 光波D. 水波4. 波的干涉现象中，以下哪个条件是必要的？A. 波源必须相同B. 波源必须不同C. 波源频率必须相同D. 波源频率必须不同5. 以下哪个选项是波的衍射现象？A. 波在障碍物后面形成阴影B. 波在障碍物后面形成增强区C. 波在障碍物前面形成阴影D. 波在障碍物前面形成增强区二、填空题（每空1分，共10分）6. 波的频率是指单位时间内波的________。

7. 波的振幅是指波的________的最大值。

8. 波的周期是指波的________完成一次循环的时间。

9. 波的波长是指相邻两个波峰之间的________。

10. 波的传播方向与振动方向垂直的波称为________。

三、简答题（每题5分，共10分）11. 简述波的干涉条件。

12. 简述波的衍射现象及其特点。

四、计算题（每题10分，共20分）13. 已知一列波在空气中的传播速度为340m/s，波长为1.7m，求该波的频率。

14. 已知一列波的频率为50Hz，振幅为0.02m，求该波在空气中的传播速度（假设声速为340m/s）。

五、论述题（每题15分，共15分）15. 论述波的多普勒效应及其在日常生活中的应用。

六、结束语通过本试题的练习，同学们应该对波动学的基本理论有了更深入的理解。

希望同学们能够将所学知识应用于实际问题中，不断提高自己的物理思维能力。

答案：一、选择题1. D2. B3. B4. C5. B二、填空题6. 完整波形7. 位移8. 振动9. 距离 10. 横波三、简答题11. 波的干涉条件包括：波源频率相同，波源相位一致，波的传播介质相同。

第10章 振动与波动一. 基本要求1. 掌握简谐振动的基本特征，能建立弹簧振子、单摆作谐振动的微分方程。

2. 掌握振幅、周期、频率、相位等概念的物理意义。

3. 能根据初始条件写出一维谐振动的运动学方程，并能理解其物理意义。

4. 掌握描述谐振动的旋转矢量法，并用以分析和讨论有关的问题。

5. 理解同方向、同频率谐振动的合成规律以及合振幅最大和最小的条件。

6. 理解机械波产生的条件。

7. 掌握描述简谐波的各物理量的物理意义及其相互关系。

8. 了解波的能量传播特征及能流、能流密度等概念。

9. 理解惠更斯原理和波的叠加原理。

掌握波的相干条件。

能用相位差或波程差概念来分析和确定相干波叠加后振幅加强或减弱的条件。

10. 理解驻波形成的条件，了解驻波和行波的区别，了解半波损失。

二. 内容提要1. 简谐振动的动力学特征 作谐振动的物体所受到的力为线性回复力，即kx F -= 取系统的平衡位置为坐标原点，则简谐振动的动力学方程（即微分方程）为x tx 222d d ω-= 2. 简谐振动的运动学特征 作谐振动的物体的位置坐标x 与时间t 成余弦（或正弦）函数关系，即)cos(ϕ+ω=t A x由它可导出物体的振动速度 )sin(ϕ+ωω-=t A v 物体的振动加速度 )cos(ϕ+ωω-=t A a 23. 振幅A 作谐振动的物体的最大位置坐标的绝对值，振幅的大小由初始条件确定，即2v ω+=2020x A4. 周期与频率 作谐振动的物体完成一次全振动所需的时间T 称为周期，单位时间内完成的振动次数γ称为频率。

周期与频率互为倒数，即ν=1T 或 T1=ν 5. 角频率(也称圆频率）ω 作谐振动的物体在2π秒内完成振动的次数，它与周期、频率的关系为 ωπ=2T 或 πν=ω26. 相位和初相 谐振动方程中（ϕ+ωt ）项称为相位，它决定着作谐振动的物体的状态。

t=0时的相位称为初相，它由谐振动的初始条件决定，即0x v ω-=ϕtan应该注意，由此式算得的ϕ在0~2π范围内有两个可能取值，须根据t=0时刻的速度方向进行合理取舍。

一、选择题：1．3001：把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时。

若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π (B) π/2 (C) 0 (D) θ ［ ］2．3002：两个质点各自作简谐振动，它们的振幅相同、周期相同。

第一个质点的振动方程为x 1 = A cos(ωt + α)。

当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处。

则第二个质点的振动方程为：(A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x ［ ］3．3007：一质量为m 的物体挂在劲度系数为k 的轻弹簧下面，振动角频率为ω。

若把此弹簧分割成二等份，将物体m 挂在分割后的一根弹簧上，则振动角频率是(A) 2 ω (B) ω2 (C) 2/ω (D) ω /2 ［ ］4．3396：一质点作简谐振动。

其运动速度与时间的曲线如图所示。

若质点的振动规律用余弦函数描述，则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 ［ ］5．3552：一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2。

将它们拿到月球上去，相应的周期分别为1T '和2T '。

则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >' ［ ］ 6．5178：一质点沿x 轴作简谐振动，振动方程为)312cos(1042π+π⨯=-t x (SI)。

振动习题一、选择题1. 对一个作简谐振动的物体，下面哪种说法是正确的 [ ](A) 物体处在运动正方向的端点时，速度和加速度都达到最大值； (B) 物体位于平衡位置且向负方向运动时，速度和加速度都为零； (C) 物体位于平衡位置且向正方向运动时，速度最大，加速度为零；(D) 物体处在负方向的端点时，速度最大，加速度为零。

2. 一沿X 轴作简谐振动的弹簧振子，振幅为A ，周期为T ，振动方程用余弦函数表示，如果该振子的初相为43π，则t=0时，质点的位置在： [ ](A) 过1x A 2=处，向负方向运动； (B) 过1x A 2=处，向正方向运动；(C) 过1x A 2=-处，向负方向运动；(D) 过1x A 2=-处，向正方向运动。

3. 一质点作简谐振动，振幅为A ，在起始时刻质点的位移为/2A ，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为 [ ](C)(3)题4. 一谐振子作振幅为A 的谐振动，它的动能与势能相等时，它的相位和坐标分别为：[ ]215(A),or ;A;(B),;3326632(C),or ;(D),;4433ππ±±π±±±π±ππ±±π±±±π±5. 一质点沿x 轴作简谐振动，振动方程为 10.04cos(2)3x t ππ=+（SI ），从t = 0时刻起，到质点位置在x = m 处，且向x 轴正方向运动的最短时间间隔为 [ ](A)s 81； (B) s 61； (C) s 41； (D) s 216. 图中所画的是两个简谐振动的振动曲线，这两个简谐振动叠加后合成的余弦振动的初相为 [ ]xtOx 1x 2(A) π23； (B) π； (C) π21 ； (D) 0一、 填空题1. 一简谐振动用余弦函数表示，振动曲线如图所示，则此简谐振动的三个特征量为： , ，2. 一质点作简谐振动，周期为T ，质点由平衡位置到二分之一最大位移处所需要的时间为 ；由最大位移到二分之一最大位移处所需要的时间为 。

波动学基础练习题及答案一、选择题1、一平面简谐波沿ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y (SI)，该波在t = 0.5 s 时刻的波形图是 ［ B ］-2、在下面几种说法中，正确的说法是： ［ C ］ (A) 波源不动时，波源的振动周期与波动的周期在数值上是不同的 (B) 波源振动的速度与波速相同(C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于π计)(D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前(按差值不大于π计)3、机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则 ［ B ］ (A) 其振幅为3 m (B) 其周期为s 31(C) 其波速为10 m/s (D) 波沿x 轴正向传播4、在简谐波传播过程中，沿传播方向相距为λ21（λ 为波长）的两点的振动速度必定［ A ］(A) 大小相同，而方向相反 (B) 大小和方向均相同 (C) 大小不同，而方向相同 (D) 大小不同，且方向相反 5、横波以波速u 沿x 轴负方向传播．t 时刻波形曲线如图．则该时刻 (A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动 (D) D 点振动速度小于零［ D ］6、一简谐波沿x 轴正方向传播，t = T /4时的波形曲线如图所示．若振动以余弦函数表示，且此题各点振动的初相取-π 到π 之间的值，则(A) O 点的初相为00=φ(B) 1点的初相为π-=211φ(C) 2点的初相为π=2φ (D) 3点的初相为π-=213φ ［ D ］7、图示一简谐波在t = 0时刻的波形图，波速 u = 200 m/s ，则P 处质点的振动速度表达式为(A) )2cos(A 2v πππ--=t (SI)． ［ A ］ (B) )cos(A 2v πππ--=t (SI)． (C) )22cos(A 2v πππ-=t (SI)．(D) )2/3cos(A 2v πππ-=t (SI)．二、 填空题1、A ，B 是简谐波波线上的两点．已知，B 点振动的相位比A 点落后π31，A 、B 两点相距0.5 m ，则该波的波长 λ = __3______ m 。

)振动学基础一、选择题：1、一质量为m 的物体挂在倔强系数为k 的轻弹簧下面，振动园频率为ω，若把此弹簧分割 为二等份，将物体m 挂在分割后的一根弹簧上，则振动园频率为： （A ）ω2。

（C ）ω2。

（C ）2ω。

（D ）22ω。

2、一质点沿x 轴作简谐振动，振动方程为))(32cos(1042SI t x ππ+⨯=-,从0=t 时刻起，到质点位置在cm x 2-=处，且向x 轴正方向运动的最短时间间隔为： （A ）s )8/1(。

（B ）s )4/1(。

（C ）s )2/1(。

（D ）s )3/1(。

（E ）s )6/1(。

3 （A ）s 62.2。

（B ）s 40.2。

（C ）s 20.2。

（D ）s 00.2。

4、已知某简谐振动的振动曲线如图所示，位移的单位为厘米，时间单位为秒，则此简谐振动方程为：（A ）cm t x )3232cos(2ππ+=。

（B ）cm t x )3232cos(2ππ-=。

（C ）cm t x 3234cos(2ππ+=。

（D ）cm t x 3234cos(2ππ-=。

（E ）cm t x )434cos(2ππ-=。

5、一弹簧振子作简谐振动，总能量为1E ，如果简谐振动动振幅增加为原来的两倍，重物的质量增为原来的四倍，则它的总能量1E 变为：（A ）4/1E 。

（B ）2/1E 。

（C ）12E 。

（D ）14E 。

6、一物体作简谐振动，振动方程为)2/cos(πω+=t A x 。

则该物体在0=t 时刻的动能与8/T t =（T 为周期）时刻的动能之比为：（A ）4:1。

（B ）2:1。

（C ）1:1。

（D ）1:2。

（E ）1:4。

7、一质点在x 轴上作简谐振动，振幅cm A 4=，周期s T 2=，其平衡位置取作坐标原点。

若0=t 时刻质点第一次通过cm x 2-=处，且向x 轴负方向运动，则质点第二次通过cm x 2-=处的时刻为： （A ）s 1。

振动和波动习题(总7页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--振动习题 一、选择题1. 对一个作简谐振动的物体，下面哪种说法是正确的 [ ](A) 物体处在运动正方向的端点时，速度和加速度都达到最大值； (B) 物体位于平衡位置且向负方向运动时，速度和加速度都为零； (C) 物体位于平衡位置且向正方向运动时，速度最大，加速度为零； (D) 物体处在负方向的端点时，速度最大，加速度为零。

2. 一沿X 轴作简谐振动的弹簧振子，振幅为A ，周期为T ，振动方程用余弦函数表示，如果该振子的初相为43π，则t=0时，质点的位置在： [ ](A) 过1x A 2=处，向负方向运动； (B) 过1x A 2=处，向正方向运动； (C) 过1x A 2=-处，向负方向运动；(D) 过1x A 2=-处，向正方向运动。

3. 一质点作简谐振动，振幅为A ，在起始时刻质点的位移为/2A ，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为 [ ](C)(3)题4. 一谐振子作振幅为A 的谐振动，它的动能与势能相等时，它的相位和坐标分别为： [ ]215(A),or ;A;(B),;3326632(C),or ;(D),;4433ππ±±π±±±π±ππ±±π±±±π±5. 一质点沿x 轴作简谐振动，振动方程为 10.04cos(2)3x t ππ=+（SI ），从t = 0时刻起，到质点位置在x = m 处，且向x 轴正方向运动的最短时间间隔为 [ ](A) s 81； (B) s 61； (C) s 41； (D) s 216. 图中所画的是两个简谐振动的振动曲线，这两个简谐振动叠加后合成的余弦振动的初相为 [ ]xtOx 1x 2(A) π23； (B) π； (C) π21 ； (D) 0一、 填空题 1. 一简谐振动用余弦函数表示，振动曲线如图所示，则此简谐振动的三个特征量为： , ，2. 一质点作简谐振动，周期为T ，质点由平衡位置到二分之一最大位移处所需要的时间为 ；由最大位移到二分之一最大位移处所需要的时间为 。

振动、波动练习题一．选择题1．一质点在X 轴上作简谐振动，振幅A=4cm 。

周期T=2s 。

其平衡位置取作坐标原点。

若t=0时刻质点第一次通过x= -2cm 处，且向X 轴负方向运动，则质点第二次通过x= -2cm 处的时刻为（ ）。

A 1sB 32s C 34s D 2s2．一圆频率为ω的简谐波沿X 轴的正方向传播，t=0时刻的波形如图所示，则t=0时刻，X 轴上各点的振动速度υ与X 轴上坐标的关系图应（ ）。

3．图示一简谐波在t=0时刻的波形图，波速υ=200m/s ，则图中O 点的振动加速度的表达式为（ ）。

)22cos(4.0)2cos(4.0)23cos(4.0)2cos(4.02222ππππππππππππ+-=--=-=-=t a D t a C t a B t a A4．频率为100Hz点振动的相位差为3π，则这两点相距（ ）。

A 2mB 2.19mC 0.5mD 28.6m5．一平面简谐波在弹性媒质中传播，媒质质元从平衡位置运动到最大位置处的过程中，（ ）。

A 它的动能转换成势能B 它的势能转换成动能C 它从相邻的一段质元获得能量其能量逐渐增大D 它把自己的能量传给相邻的一段质元，其能量逐渐减小6．在下面几种说法中，正确的说法是：（ ）。

A 波源不动时，波源的振动周期与波动的周期在数值上是不同的B 波源振动的速度与波速相同C 在波传播方向上的任一质点振动位相总是比波源的位相滞后D 在波传播方向上的任一质点振动位相总是比波源的位相超前7．一质点作简谐振动，周期为T ，当它由平衡位置向X 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为（ ）。

A 4T B 12T C 6T D 8T8．在波长为λ的驻波中两个相邻波节之间的距离为（ ）。

A λ B 3λ/4 C λ/2 D λ/49．在同一媒质中两列相干的平面简谐波的强度之比421=I I 是，则两列波的振幅之比是：（ ） A=21A A 4 B =21A A 2 C =21A A 16 D =21A A 4110．有二个弹簧振子系统，都在作振幅相同的简谐振动，二个轻质弹簧的劲度系数K 相同，但振子的质量不同。

一、选择题：（每题3分）1、把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时．若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π． (B) π/2．(C) 0 ． (D) θ． ［2、两个质点各自作简谐振动，它们的振幅相同、周期相同．第一个质点的振动方程为x 1 = A cos(ωt + α)．当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处．则第二个质点的振动方程为(A) )π21cos(2++=αωt A x ． (B) )π21cos(2-+=αωt A x ． (C) )π23cos(2-+=αωt A x ． (D) )cos(2π++=αωt A x ． ［ ］3、一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2．将它们拿到月球上去，相应的周期分别为1T '和2T '．则有(A) 11T T >'且22T T >'． (B) 11T T <'且22T T <'．(C) 11T T ='且22T T ='． (D) 11T T ='且22T T >'． ［ ］4、一弹簧振子，重物的质量为m ，弹簧的劲度系数为k ，该振子作振幅为A 的简谐振动．当重物通过平衡位置且向规定的正方向运动时，开始计时．则其振动方程为：(A) )21/(cos π+=t m k A x (B) )21/cos(π-=t m k A x (C) )π21/(cos +=t k m A x (D) )21/cos(π-=t k m A x (E) t m /k A x cos = ［ ］5、一物体作简谐振动，振动方程为)41cos(π+=t A x ω．在 t = T /4（T 为周期）时刻，物体的加速度为(A) 2221ωA -． (B) 2221ωA ． (C) 2321ωA -． (D) 2321ωA ． ［ ］6、一质点作简谐振动，振动方程为)cos(φω+=t A x ，当时间t = T /2（T 为周期）时，质点的速度为(A) φωsin A -． (B) φωsin A ．(C) φωcos A -． (D) φωcos A ． ［ ］7、一质点作简谐振动，周期为T ．当它由平衡位置向x 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为(A) T /12． (B) T /8．(C) T /6． (D) T /4． ［ ］8、两个同周期简谐振动曲线如图所示．x 1的相位比x 2的相位 (A) 落后π/2． (B) 超前π/2． (C) 落后π ． (D) 超前π．［ ］9、一质点作简谐振动，已知振动频率为f ，则振动动能的变化频率是(A) 4f . (B) 2 f . (C) f .(D) 2/f . (E) f /4 ［ ］10、一弹簧振子作简谐振动，当位移为振幅的一半时，其动能为总能量的(A) 1/4. (B) 1/2. (C) 2/1. (D) 3/4. (E) 2/3. ［ ］11、一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的(A) 7/16. (B) 9/16. (C) 11/16.(D) 13/16. (E) 15/16. ［ ］12 一质点作简谐振动，已知振动周期为T ，则其振动动能变化的周期是(A) T /4． (B) 2/T ． (C) T ．(D) 2 T ． (E) 4T ． ［ ］13、当质点以频率ν 作简谐振动时，它的动能的变化频率为(A) 4 ν． (B) 2 ν ． (C) ν． (D) ν21． ［ ］14、图中所画的是两个简谐振动的振动曲线．若这两个简谐振动可叠加，则合成的余弦振动的初相为(A) π23． (B) π． (C) π21． (D) 0． ［ ］15、若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则(A) 波速为C ． (B) 周期为1/B ．(C) 波长为 2π /C ． (D) 角频率为2π /B ． ［ ］16、下列函数f (x , t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量．其中哪个函数表示沿x 轴负向传播的行波？(A) )cos(),(bt ax A t x f +=． (B) )cos(),(bt ax A t x f -=．(C) bt ax A t x f cos cos ),(⋅=． (D) bt ax A t x f sin sin ),(⋅=． ［ ］17、频率为 100 Hz ，传播速度为300 m/s 的平面简谐波，波线上距离小于波长的两点振动的相位差为π31，则此两点相距(A) 2.86 m ． (B) 2.19 m ．A/ -A(C) 0.5 m ． (D) 0.25 m ． ［ ］18、已知一平面简谐波的表达式为 )cos(bx at A y -=（a 、b 为正值常量），则(A) 波的频率为a ． (B) 波的传播速度为 b/a ．(C) 波长为 π / b ． (D) 波的周期为2π / a ． ［ ］19、一平面简谐波的表达式为 )3cos(1.0π+π-π=x t y (SI) ，t = 0时的波形曲线如图所示，则(A) O 点的振幅为-0.1 m ．(B) 波长为3 m ． (C) a 、b 两点间相位差为π21 ． (D) 波速为9 m/s ． ［ ］20、机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则 (A) 其振幅为3 m ． (B) 其周期为s 31．(C) 其波速为10 m/s ． (D) 波沿x 轴正向传播． ［ ］21、图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形．若波的表达式以余弦函数表示，则O 点处质点振动的初相为(A) 0．(B) π21． (C) π． (D) π23． ［ ］22、一横波沿x 轴负方向传播，若t 时刻波形曲线如图所示，则在t + T /4时刻x 轴上的1、2、3三点的振动位移分别是 (A) A ，0，-A. (B) -A ，0，A. (C) 0，A ，0. (D) 0，-A ，0. ［ ］23一平面简谐波表达式为 )2(sin 05.0x t y -π-= (SI)，则该波的频率 ν (Hz)， 波速u (m/s)及波线上各点振动的振幅 A (m)依次为(A) 21，21，－0.05． (B) 21，1，－0.05． (C) 21，21，0.05． (D) 2，2，0.05． ［ ］24、在下面几种说法中，正确的说法是：(A) 波源不动时，波源的振动周期与波动的周期在数值上是不同的．(B) 波源振动的速度与波速相同．(C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于π计)．(D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前．(按差值不大于π计) ［ ］25、在简谐波传播过程中，沿传播方向相距为λ21（λ 为波长）的两点的振动速度必定x y O u(A) 大小相同，而方向相反． (B) 大小和方向均相同．(C) 大小不同，方向相同． (D) 大小不同，而方向相反．［ ］26、一平面简谐波沿x 轴负方向传播．已知 x = x 0处质点的振动方程为)cos(0φω+=t A y ．若波速为u ，则此波的表达式为(A) }]/)([cos{00φω+--=u x x t A y ． (B) }]/)([cos{00φω+--=u x x t A y ． (C) }]/)[(cos{00φω+--=u x x t A y ． (D) }]/)[(cos{00φω+-+=u x x t A y ． ［ ］27、一平面简谐波，其振幅为A ，频率为ν ．波沿x 轴正方向传播．设t = t 0时刻波形如图所示．则x = 0处质点的振动方程为(A) ]21)(2cos[0π++π=t t A y ν． (B) ]21)(2cos[0π+-π=t t A y ν． (C) ]21)(2cos[0π--π=t t A y ν． (D) ])(2cos[0π+-π=t t A y ν． ［ ］28、一平面简谐波的表达式为 )/(2cos λνx t A y -π=．在t = 1 /ν 时刻，x 1 = 3λ /4与x 2 = λ /4二点处质元速度之比是(A) -1． (B) 31． (C) 1． (D) 3 ［ ］29、在同一媒质中两列相干的平面简谐波的强度之比是I 1 / I 2 = 4，则两列波的振幅之比是(A) A 1 / A 2 = 16． (B) A 1 / A 2 = 4．(C) A 1 / A 2 = 2． (D) A 1 / A 2 = 1 /4． ［ ］30、如图所示，两列波长为λ 的相干波在P 点相遇．波在S 1点振动的初相是φ 1，S 1到P 点的距离是r 1；波在S 2点的初相是φ 2，S 2到P 点的距离是r 2，以k 代表零或正、负整数，则P 点是干涉极大的条件为：(A) λk r r =-12． (B) π=-k 212φφ． (C) π=-π+-k r r 2/)(21212λφφ． (D) π=-π+-k r r 2/)(22112λφφ．［ ］31、沿着相反方向传播的两列相干波，其表达式为)/(2cos 1λνx t A y -π= 和 )/(2cos 2λνx t A y +π=．叠加后形成的驻波中，波节的位置坐标为 (A) λk x ±=． (B) λk x 21±=． (C) λ)12(21+±=k x ． (D) 4/)12(λ+±=k x ． x y t =t 0u O其中的k = 0，1，2，3, …． ［ ］32、有两列沿相反方向传播的相干波，其表达式为)/(2cos 1λνx t A y -π= 和 )/(2cos 2λνx t A y +π=． 叠加后形成驻波，其波腹位置的坐标为：(A) x =±k λ． (B) λ)12(21+±=k x ． (C) λk x 21±=． (D) 4/)12(λ+±=k x ． 其中的k = 0，1，2，3, …． [ ]33某时刻驻波波形曲线如图所示，则a 、b 两点振动的相位差是(A) 0 (B) π21(C) π． (D) 5π/4． ［ ］34、沿着相反方向传播的两列相干波，其表达式为)/(2cos 1λνx t A y -π= 和 )/(2cos 2λνx t A y +π=．在叠加后形成的驻波中，各处简谐振动的振幅是(A) A ． (B) 2A ．(C) )/2cos(2λx A π． (D) |)/2cos(2|λx A π． ［ ］35、在波长为λ 的驻波中，两个相邻波腹之间的距离为(A) λ /4． (B) λ /2．(C) 3λ /4． (D) λ ． ［ ］36、在波长为λ 的驻波中两个相邻波节之间的距离为(A) λ ． (B) 3λ /4．(C) λ /2． (D) λ /4． ［ ］37在真空中沿着x 轴正方向传播的平面电磁波，其电场强度波的表达式是)/(2cos 0λνx t E E z -π=，则磁场强度波的表达式是：(A) )/(2cos /000λνμεx t E H y -π=． (B) )/(2cos /000λνμεx t E H z -π=．(C) )/(2cos /000λνμεx t E H y -π-=． (D) )/(2cos /000λνμεx t E H y +π-=． ［ ］38、在真空中沿着z 轴负方向传播的平面电磁波，其磁场强度波的表达式为)/(cos 0c z t H H x +-=ω，则电场强度波的表达式为：(A) )/(cos /000c z t H E y +=ωεμ． (B) )/(cos /000c z t H E x +=ωεμ． (C) )/(cos /000c z t H E y +-=ωεμ．(D) )/(cos /000c z t H E y --=ωεμ． ［ ］39、电磁波的电场强度E 、磁场强度 H 和传播速度 u 的关系是：(A) 三者互相垂直，而E 和H 位相相差π21． (B) 三者互相垂直，而且E 、H 、 u 构成右旋直角坐标系． (C) 三者中E 和H 是同方向的，但都与 u 垂直． (D) 三者中E 和H 可以是任意方向的，但都必须与 u 垂直． ［ ］40、电磁波在自由空间传播时，电场强度E 和磁场强度H(A) 在垂直于传播方向的同一条直线上．(B) 朝互相垂直的两个方向传播．(C) 互相垂直，且都垂直于传播方向．(D) 有相位差π21． ［ ］ 二、填空题：（每题4分）41、一弹簧振子作简谐振动，振幅为A ，周期为T ，其运动方程用余弦函数表示．若t = 0时，(1) 振子在负的最大位移处，则初相为______________________；(2) 振子在平衡位置向正方向运动，则初相为________________；(3) 振子在位移为A /2处，且向负方向运动，则初相为______．42、三个简谐振动方程分别为 )21cos(1π+=t A x ω，)67cos(2π+=t A x ω和)611cos(3π+=t A x ω画出它们的旋转矢量图，并在同一坐标上画出它们的振动曲线．43、一物体作余弦振动，振幅为15×10-2 m ，角频率为6π s -1，初相为0.5 π，则振动方程为x = ________________________(SI)．44、一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点．已知周期为T ，振幅为A ．(1) 若t = 0时质点过x = 0处且朝x 轴正方向运动，则振动方程为x =_____________________________．(2) 若t = 0时质点处于A x 21=处且向x 轴负方向运动，则振动方程为 x =_____________________________．45、一弹簧振子，弹簧的劲度系数为k ，重物的质量为m ，则此系统的固有振动 周期为______________________．46、在两个相同的弹簧下各悬一物体，两物体的质量比为4∶1，则二者作简谐振动的周期之比为_______________________．47、一简谐振动的表达式为)3cos(φ+=t A x ，已知 t = 0时的初位移为0.04 m ，初速度为0.09 m/s ，则振幅A =_____________ ，初相φ =________________．48、一质点作简谐振动，速度最大值v m = 5 cm/s ，振幅A = 2 cm ．若令速度具有正最大值的那一时刻为t = 0，则振动表达式为_________________________．49、两个简谐振动曲线如图所示，则两个简谐振动 的频率之比ν1∶ν2=__________________，加速度最 大值之比a 1m ∶a 2m =__________________________，初始速率之比v 10∶v 20=____________________．50、有简谐振动方程为x = 1×10-2cos(π t +φ)(SI)，初相分别为φ1 = π/2，φ2 = π，φ3 = -π/2的三个振动．试在同一个坐标上画出上述三个振动曲线．51、一简谐振动曲线如图所示，则由图可确定在t = 2s时刻质点的位移为 ____________________，速度为 __________________．52、已知两个简谐振动的振动曲线如图所示．两 简谐振动的最大速率之比为_________________．53、一水平弹簧简谐振子的振动曲线如图所示．当振子处在位移为零、速度为-ωA 、加速度为零和弹性力为零 的状态时，应对应于曲线上的________点．当振子处在位移的绝对值为A 、速度为零、加速度为-ω2A 和弹性力 为-kA 的状态时，应对应于曲线上的____________点．x (cm)t (s)O- x (cm)54、一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为A =_____________；ω =________________； φ =_______________．55、已知两个简谐振动曲线如图所示．x 1的相位比x 2 的相位超前_______．56、两个简谐振动方程分别为 t A x ωcos 1=，)31cos(2π+=t A x ω 在同一坐标上画出两者的x —t 曲线．xtO57、已知一简谐振动曲线如图所示，由图确定振子：(1) 在_____________s 时速度为零．(2) 在____________ s 时动能最大．(3) 在____________ s 时加速度取正的最大值．58、已知三个简谐振动曲线如图所示，则振动方程分别为：x 1 =______________________，x 2 = _____________________，x 3 =_______________________．59、图中用旋转矢量法表示了一个简谐振动．旋转矢量的长度为0.04 m ，旋转角速度ω = 4π rad/s ．此简谐振动以余弦函数表 x (cm)t (s)O 12示的振动方程为x =__________________________(SI)．60、一质点作简谐振动的角频率为ω 、振幅为A ．当t = 0时质点位于A x 21=处，且向x 正方向运动．试画出此振动的旋转矢量图．61、两个同方向的简谐振动曲线如图所示．合振动的振幅 为_______________________________，合振动的振动方程 为________________________________． 62、一平面简谐波．波速为6.0 m/s ，振动周期为0.1 s ，则波长为___________．在波的传播方向上，有两质点（其间距离小于波长）的振动相位差为5π /6，则此两质点相距___________．63、一个余弦横波以速度u 沿x 轴正向传播，t 时刻波形曲线如图所示．试分别指出图中A ，B ，C 各质点在 该时刻的运动方向．A _____________；B _____________ ；C ______________ ． 64、一横波的表达式是 )30/01.0/(2sin 2x t y -π=其中x 和y 的单位是厘米、t 的单位是秒，此波的波长是_________cm ，波速是_____________m/s ．65、已知平面简谐波的表达式为 )cos(Cx Bt A y -=式中A 、B 、C 为正值常量， 此波的波长是_________，波速是_____________．在波传播方向上相距为d 的两点的振动相位差是____________________．66、一声波在空气中的波长是0.25 m ，传播速度是340 m/s ，当它进入另一介质时， 波长变成了0.37 m ，它在该介质中传播速度为______________．67、已知波源的振动周期为4.00×10-2 s ，波的传播速度为300 m/s ，波沿x 轴正方向传播，则位于x 1 = 10.0 m 和x 2 = 16.0 m 的两质点振动相位差为__________．68、一平面简谐波沿x 轴正方向传播，波速 u = 100 m/s ，t = 0时刻的波形曲线如图所示． 可知波长λ = ____________； 振幅A = __________；频率ν = ____________．69、频率为500 Hz 的波，其波速为350 m/s ，相位差为2π/3 的两点间距离为________________________．70、一平面简谐波沿x 轴正方向传播．已知x = 0处的振动方程为 )cos(0φω+=t y ，波速为u ．坐标为x 1和x 2的两点的振动初相位分别记为φ 1和φ 2，则相位差φ 1－φ 2 =_________________．·---y (m)71、已知一平面简谐波的波长λ = 1 m ，振幅A = 0.1 m ，周期T = 0.5 s ．选波的传播方向为x 轴正方向，并以振动初相为零的点为x 轴原点，则波动表达式为y = _____________________________________(SI)．72、一横波的表达式是)4.0100(2sin 02.0π-π=t y (SI)， 则振幅是________，波长是_________，频率是__________，波的传播速度是______________．77、已知一平面简谐波的表达式为 )cos(bx at A -，（a 、b 均为正值常量），则波沿x 轴传播的速度为___________________．74、一简谐波的频率为 5×104 Hz ，波速为 1.5×103 m/s ．在传播路径上相距5×10-3 m 的两点之间的振动相位差为_______________．75、一简谐波沿BP 方向传播，它在B 点引起的振动方程为 t A y π=2cos 11．另一简谐波沿CP 方向传播，它在C 点引起的振动方程为)2cos(22π+π=t A y ．P 点与B 点相距0.40 m ，与C 点相距0.5 m （如图）．波速均为u = 0.20 m/s ．则两波在P 点的相位差为______________________．76、已知一平面简谐波的表达式为 )cos(Ex Dt A y -=，式中A 、D 、E 为正值常量，则在传播方向上相距为a 的两点的相位差为______________．77、在简谐波的一条射线上，相距0.2 m 两点的振动相位差为π /6．又知振动周期为0.4 s ，则波长为_________________，波速为________________．78、一声纳装置向海水中发出超声波，其波的表达式为)2201014.3cos(102.153x t y -⨯⨯=- (SI)则此波的频率ν = _________________ ，波长λ = __________________， 海水中声速u = __________________．79、已知14℃时的空气中声速为340 m/s ．人可以听到频率为20 Hz 至20000 Hz 范围内的声波．可以引起听觉的声波在空气中波长的范围约为______________________________．80、一平面简谐波（机械波）沿x 轴正方向传播，波动表达式为)21cos(2.0x t y π-π= (SI)，则x = -3 m 处媒质质点的振动加速度a 的表达式为________________________________________．81、在同一媒质中两列频率相同的平面简谐波的强度之比I 1 / I 2 = 16，则这两列波的振幅之比是A 1 / A 2 = ____________________．82、两相干波源S 1和S 2的振动方程分别是)cos(1φω+=t A y 和)cos(2φω+=t A y . S 1距P 点3个波长，S 2距P 点 4.5个波长．设波传播过程中振幅不变，则两波同时传到P 点时的合振幅是________________．83、两相干波源S 1和S 2的振动方程分别是t A y ωcos 1=和)21cos(2π+=t A y ω．S 1距P 点3个波长，S 2距P 点21/4个波长．两波在P 点引起的两个振动的相位差是____________．84、两个相干点波源S 1和S 2，它们的振动方程分别是 )21cos(1π+=t A y ω和 )21cos(2π-=t A y ω．波从S 1传到P 点经过的路程等于2个波长，波从S 2传到P 点的路程等于7 / 2个波长．设两波波速相同，在传播过程中振幅不衰减，则两波传到P 点的振动的合振幅为__________________________．85、一弦上的驻波表达式为)90cos()cos(1.0t x y ππ=(SI)．形成该驻波的两个反向传播的行波的波长为________________，频率为__________________．86、一弦上的驻波表达式为 t x y 1500cos 15cos 100.22-⨯= (SI)．形成该驻波的两个反向传播的行波的波速为__________________．87、在弦线上有一驻波，其表达式为 )2cos()/2cos(2t x A y νλππ=, 两个相邻波节之间的距离是_______________．88、频率为ν = 5×107 Hz 的电磁波在真空中波长为_______________m ，在折射率为n = 1.5 的媒质中波长为______________m ．89、在电磁波传播的空间（或各向同性介质）中，任一点的E 和H 的方向及波传播方向之间的关系是：_________________________________________________________________________________________________________．90、在真空中沿着x 轴正方向传播的平面电磁波，其电场强度波的表达式为)/(2cos 600c x t E y -π=ν (SI)，则磁场强度波的表达式是______________________________________________________．(真空介电常量 ε 0 = 8.85×10-12 F/m ，真空磁导率 μ 0 =4π×10-7 H/m)91、在真空中沿着x 轴负方向传播的平面电磁波，其电场强度的波的表达式为)/(2cos 800c x t E y +π=ν (SI)，则磁场强度波的表达式是________________________________________________________．(真空介电常量 ε 0 = 8.85×10-12 F/m ，真空磁导率 μ 0 =4π×10-7 H/m)92、在真空中沿着z 轴正方向传播的平面电磁波的磁场强度波的表达式为])/(cos[00.2π+-=c z t H x ω (SI)，则它的电场强度波的表达式为____________________________________________________．（真空介电常量 ε 0 = 8.85×10-12 F/m ，真空磁导率 μ 0 =4π×10-7 H/m ）93、在真空中沿着负z 方向传播的平面电磁波的磁场强度为)/(2cos 50.1λνz t H x +π= (SI)，则它的电场强度为E y = ____________________． （真空介电常量ε 0 = 8.85×10-12 F/m ，真空磁导率 μ 0 =4π×10-7 H/m ）94真空中一简谐平面电磁波的电场强度振幅为 E m = 1.20×10-2 V/m 该电磁波的强度为_________________________．（真空介电常量 ε 0 = 8.85×10-12 F/m ，真空磁导率 μ 0 =4π×10-7 H/m ）95、在真空中沿着z 轴的正方向传播的平面电磁波，O 点处电场强度为)6/2cos(900π+π=t E x ν，则O 点处磁场强度为___________________________． （真空介电常量 ε 0 = 8.85×10-12 F/m ，真空磁导率 μ 0 =4π×10-7 H/m ）96、在地球上测得来自太阳的辐射的强度=S 1.4 kW/m 2．太阳到地球的距离约为1.50×1011 m ．由此估算，太阳每秒钟辐射的总能量为__________________．97、在真空中沿着z 轴负方向传播的平面电磁波，O 点处电场强度为)312cos(300π+π=t E x ν (SI)，则O 点处磁场强度为_____________________________________．在图上表示出电场强度，磁场强度和传播速度之间的相互关系．98、电磁波在真空中的传播速度是_________________(m/s)（写三位有效数字）．99、电磁波在媒质中传播速度的大小是由媒质的____________________决定的．100、电磁波的E 矢量与H 矢量的方向互相____________，相位__________．三、计算题：（每题10分）101、一质点按如下规律沿x 轴作简谐振动：)328cos(1.0π+π=t x (SI)．求此振动的周期、振幅、初相、速度最大值和加速度最大值．102、一质量为0.20 kg 的质点作简谐振动，其振动方程为)215cos(6.0π-=t x (SI)．求：(1) 质点的初速度；(2) 质点在正向最大位移一半处所受的力．z yxO103、有一轻弹簧，当下端挂一个质量m 1 = 10 g 的物体而平衡时，伸长量为 4.9 cm ．用这个弹簧和质量m 2 = 16 g 的物体组成一弹簧振子．取平衡位置为原点，向上为x 轴的正方向．将m 2从平衡位置向下拉 2 cm 后，给予向上的初速度v 0 = 5 cm/s 并开始计时，试求m 2的振动周期和振动的数值表达式．104、有一单摆，摆长为l = 100 cm ，开始观察时( t = 0 )，摆球正好过 x 0 = -6 cm 处，并以v 0 = 20 cm/s 的速度沿x 轴正向运动，若单摆运动近似看成简谐振动．试求(1) 振动频率； (2) 振幅和初相．105、质量m = 10 g 的小球与轻弹簧组成的振动系统，按)318cos(5.0π+π=t x 的规律作自由振动，式中t 以秒作单位，x 以厘米为单位，求(1) 振动的角频率、周期、振幅和初相；(2) 振动的速度、加速度的数值表达式；(3) 振动的能量E ；(4) 平均动能和平均势能．106、一质量m = 0.25 kg 的物体，在弹簧的力作用下沿x 轴运动，平衡位置在原点. 弹簧的劲度系数k = 25 N ·m -1．(1) 求振动的周期T 和角频率ω．(2) 如果振幅A =15 cm ，t = 0时物体位于x = 7.5 cm 处，且物体沿x 轴反向运动，求初速v 0及初相φ．(3) 写出振动的数值表达式．107、一质量为10 g 的物体作简谐振动，其振幅为2 cm ，频率为4 Hz ，t = 0时位移为 －2 cm ，初速度为零．求(1) 振动表达式；(2) t = (1/4) s 时物体所受的作用力．108、两个物体作同方向、同频率、同振幅的简谐振动．在振动过程中，每当第一个物体经过位移为2/A 的位置向平衡位置运动时，第二个物体也经过此位置，但向远离平衡位置的方向运动．试利用旋转矢量法求它们的相位差．109、一物体质量为0.25 kg ，在弹性力作用下作简谐振动，弹簧的劲度系数k = 25 N ·m -1，如果起始振动时具有势能0.06 J 和动能0.02 J ，求(1) 振幅；(2) 动能恰等于势能时的位移；(3) 经过平衡位置时物体的速度．110、在一竖直轻弹簧下端悬挂质量m = 5 g 的小球，弹簧伸长∆l = 1 cm 而平衡．经推动后，该小球在竖直方向作振幅为A = 4 cm 的振动，求(1) 小球的振动周期； (2) 振动能量．111、一物体质量m = 2 kg ，受到的作用力为F = -8x (SI)．若该物体偏离坐标原点O 的最大位移为A = 0.10 m ，则物体动能的最大值为多少？112、一横波沿绳子传播，其波的表达式为)2100cos(05.0x t y π-π= (SI)(1) 求此波的振幅、波速、频率和波长．(2) 求绳子上各质点的最大振动速度和最大振动加速度．(3) 求x 1 = 0.2 m 处和x 2 = 0.7 m 处二质点振动的相位差．113、一振幅为 10 cm ，波长为200 cm 的简谐横波,沿着一条很长的水平的绷紧弦从左向右行进，波速为 100 cm/s ．取弦上一点为坐标原点，x 轴指向右方，在t = 0时原点处质点从平衡位置开始向位移负方向运动．求以SI 单位表示的波动表达式（用余弦函数）及弦上任一点的最大振动速度．114、一振幅为 10 cm ，波长为200 cm 的一维余弦波．沿x 轴正向传播，波速为 100 cm/s ，在t = 0时原点处质点在平衡位置向正位移方向运动．求(1) 原点处质点的振动方程．(2) 在x = 150 cm 处质点的振动方程．115、一简谐波沿x 轴负方向传播，波速为1 m/s ，在x 轴上某质点的振动频率为1 Hz 、振幅为0.01 m ．t = 0时该质点恰好在正向最大位移处．若以该质点的平衡位置为x 轴的原点．求此一维简谐波的表达式．116、已知一平面简谐波的表达式为 )37.0125cos(25.0x t y -= (SI)(1) 分别求x 1 = 10 m ，x 2 = 25 m 两点处质点的振动方程；(2) 求x 1，x 2两点间的振动相位差；(3) 求x 1点在t = 4 s 时的振动位移．117、一横波方程为 )(2cos x ut A y -π=λ， 式中A = 0.01 m ，λ = 0.2 m ，u = 25 m/s ，求t = 0.1 s 时在x = 2 m 处质点振动的位移、速度、加速度．118、如图，一平面简谐波沿Ox 轴传播，波动表达式为])/(2cos[φλν+-π=x t A y (SI)，求 (1) P 处质点的振动方程； (2) 该质点的速度表达式与加速度表达式．119、一平面简谐波，频率为300 Hz ，波速为340 m/s ，在截面面积为3.00×10-2 m 2的管内空气中传播，若在10 s 内通过截面的能量为2.70×10-2 J ，求(1) 通过截面的平均能流；(2) 波的平均能流密度；(3) 波的平均能量密度．120、一驻波中相邻两波节的距离为d = 5.00 cm ，质元的振动频率为ν =1.00×103 Hz ，求形成该驻波的两个相干行波的传播速度u 和波长λ ．O P大学物理------振动与波参考答案一、选择题1 - 5 CBDBB 6 -10 BCBBD 11-15 EBBBC 16-20 ACDCB 21-25 DBCCA 26-30 ABACD 31-35 DCCDB 36-40 CCCBC二、填空题41.（1） π； （2）2/π-； （3）3/π； 42. 略； 43. 21510cos[6]2t ππ-⨯+； 44. （1）2cos[]2A t T ππ-， (2) 2cos[]3A t T πλ+；45. 2 46. 1:2； 47. m 05.0，π205.0- or 09.36-； 48. 25210cos[]22x t π-=⨯- ； 49. 1:2，1:4，1:2； 51. 0，s m /3； 52. 1:1； 53. e a f b ,,,；54. cm 10，s rad /6/π，3/π；55. 3/4π； 56. 略 ；57.（1）,...2,1,0,2/)12(=+n n ，（2）,...2,1,0,=n n ，（3）,...2,1,0,2/)14(=+n n ，； 58. t πcos 1.0，)2/cos(1.0ππ-t ，)cos(1.0ππ±t ； 59. ]24cos[04.0ππ-t ； 60. 略； 61. 21A A -， ]22cos[12ππ+-=t T A A x ； 62. m 6.0，m 25.0； 63. 向下，向上；64. cm 30，30； 65. c /2π，c B /，cd ； 66. s m /503；67. π；68. m 8.0，m 2.0，Hz 125；69. m 233.0；70. u x x /)(12-ω；71. ]24cos[1.0x t ππ-；72. cm 2，cm 5.2，Hz 100，51~2500；73. b a /； 74. 3/π； 75. 0；76. aE ； 77. m 4.2， s m /0.6；78. Hz 4100.5⨯，m 21086.2-⨯，s m /1043.13⨯； 79. m 2107.1~17-⨯； 80. )23cos(2.02x t πππ+-； 81. 4； 82. 0； 83. 0； 84. A 2； 85. m 2，Hz 45； 86. s m /100； 87. 2/λ； 88. m 6， m 4； 89. H E S ⨯= ； 90. )](2cos[59.1c x t H z -=πν； 91. )](2cos[12.2cx t H z +-=πν； 92. ])(cos[754πω+--=c z t E y ； 93. )](2cos[565λνπz t +； 94. 271091.1--⨯wm ；95. ]62cos[39.2ππν+=t H y ； 96. J 26100.4⨯；97. ]32cos[796.0ππν+-=t H y ；98. 81000.3⨯； 99. με,； 100. 垂直，相同，相同三、计算题101、解：周期 25.0/2=π=ωT s ，振幅 A = 0.1 m ，初相 φ = 2π/3，v max = ω A = 0.8π m/s ( = 2.5 m/s )，a max = ω 2A = 6.4π2 m/s 2 ( =63 m/s 2 )．102、解：(1) )25sin(0.3d d π--==t t x v (SI) t 0 = 0 , v 0 = 3.0 m/s ．(2) x m ma F 2ω-==A x 21= 时， F = -1.5 N ． 103、解：设弹簧的原长为l ，悬挂m 1后伸长∆l ，则 k ∆l = m 1g ，k = m 1g/ ∆l = 2 N/m取下m 1上m 2后， 2.11/2==m k ω rad/sω/2π=T =0.56 st = 0时， φcos m 10220A x =⨯-=-φωsin m/s 10520A -=⨯=-v解得 220201005.2m )/(-⨯=+=ωv x A m =-=-)/(tg 001x ωφv 180°+12.6°=3.36 rad也可取 φ = -2.92 rad振动表达式为 x = 2.05×10-2cos(11.2t -2.92) (SI)或 x = 2.05×10-2cos(11.2t +3.36) (SI)104、解：(1) 13.3/==l g ω rad/s ，5.0)2/(=π=ων Hz(2) t = 0 时，x 0 = -6 cm= A cos φ， v 0 = 20 cm/s= -A ω sin φ由上二式解得 A = 8.8 cm ，φ = 180°＋46.8°= 226.8°= 3.96 rad ，（或－2.33 rad ）105、解：(1) A = 0.5 cm ；ω = 8π s -1；T = 2π/ω = (1/4) s ；φ = π/3 (2) )318sin(1042π+π⨯π-==-t x v (SI))318cos(103222π+π⨯π-==-t x a (SI)(3) 2222121A m kA E E E P K ω==+==7.90×10-5 J(4) 平均动能 ⎰=TK t m T E 02d 21)/1(v⎰π+π⨯π-=-T t t m T 0222d )318(sin )104(21)/1(= 3.95×10-5 J = E 21同理 E E P 21== 3.95×10-5 J106、解： (1) 1s 10/-==m k ω， 63.0/2=π=ωT s(2) A = 15 cm ，在 t = 0时，x 0 = 7.5 cm ，v 0 < 0由 2020)/(ωv +=x A得 3.12020-=--=x A ωv m/sπ=-=-31)/(tg 001x ωφv 或 4π/3∵ x 0 > 0 ，∴ π=31φ(3) )3110cos(10152π+⨯=-t x (SI)107、解：(1) t = 0时，x 0 = -2 cm = -A , 故初相 φ = π ，ω = 2 πν = 8 π s -1)8cos(1022π+π⨯=-t x (SI)(2) t = (1/4) s 时，物体所受的作用力 126.02=-=x m F ω N 108、解：依题意画出旋转矢量图。