整式的乘除培优

（完整版）整式的乘除培优（可编辑修改word版）整式的乘除培优⼀、选择题：1﹒已知x a＝2，x b＝3，则x3a+2b 等于（）A﹒17 B﹒72 C﹒24 D﹒362﹒下列计算正确的是（）A﹒5x6·(－x3)2＝－5x12 B﹒(x2+3y)(3y－x2)＝9y2－x4C﹒8x5÷2x5＝4x5 D﹒(x－2y)2＝x2－4y23、已知M＝20162，N＝2015×2017，则M 与N 的⼤⼩是（）A﹒M＞N B﹒M＜N C﹒M＝N D﹒不能确定4、已知x2－4x－1＝0，则代数式 2x(x－3)－(x－1)2+3 的值为（）A﹒3 B﹒2 C﹒1 D﹒－15、若a x ÷a y ＝a2，(b x)y＝b3，则(x+y)2的平⽅根是（）A﹒4 B﹒±4C﹒±6D﹒166、计算-(a -b)4 (b -a)3 的结果为（）A、-(a -b)7B、-(a +b)7C、(a-b)7D、(b-a)77、已知a=8131，b=2741，c=961，则a，b，c 的⼤⼩关系是（）B、A．a＞b＞c B．a＞c＞b C．a＜b＜c D．b＞c＞a8、图①是⼀个边长为（m+n）的正⽅形，⼩颖将图①中的阴影部分拼成图②的形状，由图①和图②能验证的式⼦是（）A．（m+n）2﹣（m﹣n）2=4mn B．（m+n）2﹣（m2+n2）=2mnC．（m﹣n）2+2mn=m2+n2 D．（m+n）（m﹣n）=m2﹣n29、若a﹣2=b+c，则a（a﹣b﹣c）+b（b+c﹣a）﹣c（a﹣b﹣c）的值为（）=90 pA．4 B．2 C．1 D．810、当x=1 时，ax+b+1 的值为﹣2，则（a+b﹣1）（1﹣a﹣b）的值为（）A．﹣16 B．﹣8 C．8 D．1611、已知a2+a﹣3=0，那么a2（a+4）的值是（）A．9 B．﹣12 C．﹣18 D．﹣1512、在求1+6+62+63+64+65+66+67+68+69 的值时，⼩林发现：从第⼆个加数起每⼀个加数都是前⼀个加数的6 倍，于是她设：S=1+6+62+63+64+65+66+67+68+69①，然后在①式的两边都乘以6，得：6S=6+62+63+64+65+66+67+68+69+610②，②﹣①得6S﹣S=610﹣1，即5S=610﹣1，所以S=，得出答案后，爱动脑筋的⼩林想：如果把“6”换成字母“a”（a≠0 且a≠1），能否求出1+a+a2+a3+a4+…+a2014 的值？你的答案是（）A． B． C． D．a2014﹣1⼆、填空：1、若ax3m y12÷3x3y2n＝4x6y8，则(2m+n－a)n＝﹒2、若(2x+3y)(mx－ny)＝4x2－9y2，则mn＝.3. 已知a+b＝8，a2b2＝4，则1(a2+b2)－ab＝. 2999 p999 , q =119，那么9q (填＞，＜或=)5.已知10a= 20, 10b=1，则3a÷ 3b= 56.设A =(x -3)(x - 7)，B =(x - 2)(x -8)，则A B（填＞，＜，或=）7.若关于x 的多项式x2-8x +m =(x - 4)2 ，则m 的值为若关于x 的多项式x2+nx +m2=(x - 4)2 ，则m n=4. 若225 4 3 2 1 3 1 若关于 x 的多项式 x 2 + nx + 9 是完全平⽅式，则 n=8.计算： 20162 - 2015? 2016 =9. 计算： ?1- 1 ??1- 1 ? ?1- 1 ??1- 1 ? =? 32 ? 992 1002 ? 10.计算： (2 +1)(22 +1)(24 +1)(22n+1)=11、已知：(x +1)5 = a x 5 + a x 4 + a x 3 + a x 2+ a x + a ，则 a + a + a =12、已知： x 2 - (m - 2)x + 36 是完全平⽅式，则 m=13、已知：x 2 + y 2- 6 y = 2x - 10 ，则 x - y =14、已知：13x 2 - 6xy + y 2 - 4x +1 = 0 ，则(x + y )2017 x 2016= 15、若 P = a 2 + 2b 2 + 2a + 4b + 2017 ，则 P 的最⼩值是=16、已知 a =1 2018 x2 + 2018，b = 1 2018 x 2 + 2017，c = 1 2018x 2+ 2016 ，则 a 2 + b 2 + c 2 - ab - bc - ac 的值为17、已知(2016 - a )(2018 - a ) = 2017 ，则(2016 - a )2 + (2018 - a )2 =x - 1 18、已知 x x 2 5，则 x 4+ 1 =19、已知： x 2 - 3x - 1 = 0 ，则 x 2 + 1x2三、解答题：=， x 4 +1=x41、（x 2－2x －1）（x 2＋2x －1）；②（2m+n ﹣p ）（2m ﹣n+p ）2、形如 a b c的式⼦叫做⼆阶⾏列式，它的运算法则⽤公式表⽰为da c = ad - bc ，⽐如 2b d 1 5= 2 ? 3 -1? 5 = 1，请按照上述法则计算 30 5 =-2ab -3ab2a2b(-ab)2的结果。

整式的乘除培优课教师寄语：.书山有路勤为径，学海无涯苦作舟。

【知识精要】 :1幂的运算性质：①〔、为正整数〕②〔为正整数〕③〔、为正整数〕④〔、为正整数，且〕〔〕〔，为正整数〕2整式的乘法公式：①②③3.科学记数法，其中4 单项式的乘法法那么：单项式与单项式相乘，把他们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，那么连同它的指数作为积的一个因式。

5. 单项式乘以多项式：就是用单项式去乘多项式的每一项，再把所得的积相加，多项式与多项式相乘的法那么；6．多项式与多项式相乘：先用多项式的每一项乘以另一个多项式的每一项，再把所的的积相加。

7 单项式的除法法那么： 单项式相除，把系数、同底数幂分别相除， 作为商的因式，对于只在被除式里含有的字母，那么连同它的指数作为商的一个因式。

8 多项式除以单项式：先把这个多项式的每一项除以这个单项式，在把所的的商相加。

【例题剖析】 :例 1, 计算:21、(a ＋ b ＋ c)(a － b － c)2a b c，,3 、 20212－2021×2007 4、 (2a-b)2(b+2a) 2例2，求 的值。

例3 [ 例2]， ，求 的值。

例4 [例 3]，求的值。

例5 [ 例4]，，求的值。

【课堂精练】 :1.〔为偶数〕2.用科学记数法表示为3.4.5.6.7.假设，那么8.若是，那么=〔〕A. B. C. D.9.所得结果是〔〕A. B. C.10.为正整数，假设能被整除，那么整数的取值范围是〔〕A. B. C. D.11.要使成为一个完好平方式，那么的值为〔〕A. B. C. D.12.以下各式能用平方差公式计算的是〔〕A. B.C. D.13.计算：〔1〕〔2〕〔3〕〔为正整数〕〔4〕【培优拓展】 :1. ，求的值。

2.假设，求的值。

3.，求的值。

4. 己知 x+5y=6 ,求x2+5xy+30y的值。

5 算〔 1－1〕〔1－1〕〔1－1〕⋯〔 1－1〕〔 1－1〕的．223242921026. 假设〔x2＋px＋q〕〔x2－ 2x－ 3〕张开后不含x2， x3，求 p、 q 的．7．〔a－ 1〕〔b－ 2〕－a〔b－ 3〕＝ 3，求代数式? 〔a2 +b2 〕－ ab 的．8.化简求值： [ 〔x＋1y〕2＋〔x－1y〕2] 〔 2x2－1y2〕，其中x＝－ 3，y＝ 4．2229. 填空①. 设4x2mx 121 是一个完好平方式，那么 m =_______。

北师⼤版七年级下册第1章《整式的乘除》培优拔尖习题训练（带答案）北师⼤版第1章《整式的乘除》培优拔尖习题训练⼀．选择题（共10⼩题）1．下⾯计算正确的是（）A．a2?a3＝a5B．3a2﹣a2＝2C．4a6÷2a3＝2a2D．（a2）3＝a52．化简（x+4）（x﹣1）+（x﹣4）（x+1）的结果是（）A．2x2﹣8B．2x2﹣x﹣4C．2x2+8D．2x2+6x3．若要使4x2+mx+成为⼀个两数差的完全平⽅式，则m的值应为（）A．B．C．D．4．下列计算错误的是（）A．（﹣2a3）3＝﹣8a9B．（ab2）3?（a2b）2＝a7b8C．（xy2）2?（9x2y）＝x6y6D．（5×105）×（4×104）＝2×10105．已知长⽅形ABCD可以按图⽰⽅式分成九部分，在a，b变化的过程中，下⾯说法正确的有（）①图中存在三部分的周长之和恰好等于长⽅形ABCD的周长②长⽅形ABCD的长宽之⽐可能为2③当长⽅形ABCD为正⽅形时，九部分都为正⽅形④当长⽅形ABCD的周长为60时，它的⾯积可能为100．A．①②B．①③C．②③④D．①③④6．若（x2+x+b）?（2x+c）＝2x3+7x2﹣x+a，则a，b，c的值分别为（）A．a＝﹣15，b＝﹣3，c＝5B．a＝﹣15，b＝3，c ＝﹣5C．a＝15，b＝3，c＝5D．a＝15，b＝﹣3，c＝﹣57．如图1，在边长为a的正⽅形中剪去⼀个边长为b的⼩正⽅形（a＞b），把剩下部分沿图1中的虚线剪开后重新拼成⼀个梯形（如图2），利⽤这两幅图形⾯积，可以验证的乘法公式是（）A．（a﹣b）2＝a2﹣2ab+b2B．（a+b）2＝a2+2ab+b2C．a（a+b）＝a2+ab D．（a+b）（a﹣b）＝a2﹣b28．若（a﹣c+b）2＝21，（a+c+b）2＝2019，则a2+b2+c2+2ab的值是（）A．1020B．1998C．2019D．20409．我们知道，同底数幂的乘法法则为a m?a n＝a m+n（其中a≠0，m、n为正整数），类似地我们规定关于任意正整数m、n的⼀种新运算：h（m+n）＝h（m）?h（n）；⽐如h（2）＝3，则h（4）＝h（2+2）＝3×3＝9，若h（2）＝k（k≠0），那么h（2n）?h（2020）的结果是（）A．2k+2020B．2k+1010C．k n+1010D．1022k10．观察下列各式：（x2﹣1）÷（x﹣1）＝x+1．（x3﹣1）÷（x﹣1）＝x2+x+1，（x4﹣1）÷（x﹣1）＝x3+x2+x+1，（x5﹣1）÷（x﹣1）＝x4+x3+x2+x+1，根据上述规律计算2+22+23+…+262+263的值为（）A．264﹣1B．264﹣2C．264+1D．264+2⼆．填空题（共8⼩题）11．2015年诺贝尔⽣理学或医学奖得主中国科学家屠呦呦，发现了⼀种长度约为0.000000456毫⽶的病毒，把0.000000456⽤科学记数法表⽰为．12．已知x2﹣2（m+3）x+9是⼀个完全平⽅式，则m＝．13．计算：（16x3﹣8x2+4x）÷（﹣2x）＝．14．若计算（x﹣2）（3x+m）的结果中不含关于字母x的⼀次项，则m的值为．15．若（x﹣2）x＝1，则x＝．16．如图所⽰，如图，边长分别为a和b的两个正⽅形拼接在⼀起，则图中阴影部分的⾯积为．17．在我们所学的课本中，多项式与多项式相称可以⽤⼏何图形的⾯积来表⽰，例如：（2a+b）（a+b）＝2a2+3ab+b2就可以⽤下⾯图中的图①来表⽰．请你根据此⽅法写出图②中图形的⾯积所表⽰的代数恒等式：18．观察下列各等式：x﹣2＝x﹣2（x﹣2）（x+2）＝x2﹣22（x﹣2）（x2+2x+4）＝x3﹣23（x﹣2）（x3+2x2+4x+8）＝x4﹣24……请你猜想：若A?（x+y）＝x5+y5，则代数式A＝．19．先化简，再求值：（m﹣2）2﹣（n+2）（n﹣2）﹣m（m﹣1），其中2m2+12m+18+|2n﹣3|＝0．20．计算：（1）（﹣4x2）﹣（1+2x）（8x﹣2）（2）（﹣2x﹣y）（y﹣2x）﹣（2x+y）2（3）先化简再求值：（12x3y2+x2y﹣x2y3）÷（﹣2x2y）﹣[2（x﹣y）]2，其中x＝﹣，y＝321．阅读材料：（1）1的任何次幂都为1：（2）﹣1的奇数次幂为﹣1：（3）﹣1的偶数次幂为1：（4）任何不等于零的数的零次幂为1．请问当x为何值时，代数式（2x+3）x+2020的值为1．22．（1）先化简，再求值已知：[（x﹣2y）2﹣4y2+2xy]÷2x，其中x＝1，y＝2．（2）先化简，再求值：（﹣3ab）2（a2+ab+b2）﹣3ab（3a3b+3a2b2﹣ab3），其中a＝﹣，b＝23．（1）计算：（a﹣2）（a2+2a+4）＝．（2x﹣y）（4x2+2xy+y2）＝．（2）上⾯的整式乘法计算结果很简洁，你⼜发现⼀个新的乘法公式（请⽤含a，b的字母表⽰）．（3）下列各式能⽤你发现的乘法公式计算的是．A．（a﹣3）（a2﹣3a+9）B．（2m﹣n）（2m2+2mn+n2）C．（4﹣x）（16+4x+x2）D．（m﹣n）（m2+2mn+n2）24．如图1，在⼀个边长为a的正⽅形⽊板上锯掉⼀个边长为b的正⽅形，并把余下的部分沿虚线剪开拼成图2的形状．（1）请⽤两种⽅法表⽰阴影部分的⾯积：图1得：；图2得；（2）由图1与图2⾯积关系，可以得到⼀个等式：；（3）利⽤（2）中的等式，已知a2﹣b2＝16，且a+b＝8，则a﹣b＝．参考答案1．【解答】解：A、结果是a5，故本选项符合题意；B、结果是2a2，故本选项不符合题意；C、结果是2a3，故本选项不符合题意；D、结果是a6，故本选项不符合题意；故选：A．2．【解答】解：（x+4）（x﹣1）+（x﹣4）（x+1）＝x2+3x﹣4+x2﹣3x﹣4＝2x2﹣8，故选：A．3．【解答】解：∵（2x﹣）2＝4x2﹣x+，或[2x﹣（﹣）]2＝4x2+x+，∴m＝﹣或．故选：A．4．【解答】解：A、（﹣2a3）3＝﹣8a9，正确；B、（ab2）3?（a2b）2＝a7b8，正确；C、（xy2）2?（9x2y）＝x4y5，错误；D、（5×105）×（4×104）＝2×1010，正确；故选：C．5．【解答】解：①四边形AEFG、FHKM、SKWC的周长之和等于长⽅形ABCD的周长；②长⽅形的长为a+2b，宽为2a+b，若该长⽅形的长宽之⽐为2，则a+2b＝2（2a+b）解得a＝0．这与题意不符，故②的说法不正确；③当长⽅形ABCD为正⽅形时，2a+b＝a+2b所以a＝b，所以九部分都为正⽅形，故③的说法正确；④当长⽅形ABCD的周长为60时，即2（2a+b+a+2b）＝60整理，得a+b＝10所以四边形GHWD的⾯积为100．故当长⽅形ABCD的周长为60时，它的⾯积不可能为100，故④的说法不正确．综上正确的是①③．故选：B．6．【解答】解：∵（x2+x+b）?（2x+c）＝2x3+7x2﹣x+a，2x3+2x2+2bx+cx2+cx+bc＝2x3+7x2﹣x+a，2x3+（2+c）x2+（2b+c）x+bc∴2+c＝7，2b+c＝﹣1，bc＝a．解得c＝5，b＝﹣3，a＝﹣15．故选：A．7．【解答】解：图1阴影部分的⾯积等于a2﹣b2，图2梯形的⾯积是（2a+2b）（a﹣b）＝（a+b）（a﹣b）根据两者阴影部分⾯积相等，可知（a+b）（a﹣b）＝a2﹣b2⽐较各选项，只有D符合题意故选：D．8．【解答】解：（a﹣c+b）2＝a2+b2+c2﹣2ac﹣2bc+2ab＝21①，（a+c+b）2＝a2+b2+c2+2ac+2bc+2ab＝2019②，①+②，得2（a2+b2+c2）+4ab＝2040，a2+b2+c2+2ab＝1020．故选：A．9．【解答】解：∵h（2）＝k（k≠0），h（m+n）＝h（m）?h（n），∴h（2n）?h（2020）＝h（）?h（）＝?＝k n?k1010＝k n+1010，故选：C．10．【解答】解：有上述规律可知：（x64﹣1）÷（x﹣1）＝x63+x62+…+x2+x+1当x＝2时，即（264﹣1）÷（2﹣1）＝1+2+22+…+262+263∴2+22+23+…+262+263＝264﹣2．故选：B．⼆．填空题（共8⼩题）11．【解答】解：把0.000000456⽤科学记数法表⽰为4.56×10﹣7，故答案为：4.56×10﹣7．12．【解答】解：∵x2﹣2（m+3）x+9是⼀个完全平⽅式，∴m+3＝±3，解得：m＝﹣6或m＝0，故答案为：﹣6或013．【解答】解：（16x3﹣8x2+4x）÷（﹣2x）＝﹣8x2+4x﹣2．故答案为：﹣8x2+4x﹣2．14．【解答】解：原式＝3x2+（m﹣6）x﹣2m，由结果不含x的⼀次项，得到m﹣6＝0，解得：m＝6，故答案为：615．【解答】解：∵（x﹣2）x＝1，∴x＝0时，（0﹣2）0＝1，当x＝3时，（3﹣2）3＝1，则x＝0或3．故答案为：0或3．16．【解答】解：∵去掉△DEF，则剩余部分为⼀个直⾓梯形∴图中阴影部分的⾯积为：（a+a+b）b﹣（b﹣a）a﹣（a+b）a＝ab+b2﹣ab+a2﹣a2﹣ab＝b2故答案为：．17．【解答】解：根据图形列得：（a+2b）（2a+b）＝2a2+5ab+2b2．故答案为：（a+2b）（2a+b）＝2a2+5ab+2b2．18．【解答】解：（x4﹣x3y+x2y2﹣xy3+y4）（x+y）＝x5+y5，故答案为：x4﹣x3y+x2y2﹣xy3+y4．三．解答题（共6⼩题）19．【解答】解：（m﹣2）2﹣（n+2）（n﹣2）﹣m（m﹣1）＝m2﹣4m+4﹣n2+4﹣m2+m＝﹣n2﹣3m+8，∵2m2+12m+18+|2n﹣3|＝0，∴2（m+3）2+|2n﹣3|＝0，∴m+3＝0，2n﹣3＝0，∴m＝﹣3，n＝1.5，当m＝﹣3，n＝1.5时，原式＝﹣1.52﹣3×（﹣3）+8＝﹣3．20．【解答】解：（1）（﹣4x2）﹣（1+2x）（8x﹣2）＝﹣4x2﹣8x+2﹣16x2+4x＝﹣20x2﹣4x+2；（2）（﹣2x﹣y）（y﹣2x）﹣（2x+y）2＝4x2﹣y2﹣4x2﹣4xy﹣y2＝﹣2y2﹣4xy；（3）（12x3y2+x2y﹣x2y3）÷（﹣2x2y）﹣[2（x﹣y）]2＝﹣6xy+y2﹣4x2+8xy﹣4y2＝2xy﹣4x2﹣y2﹣，当，y＝3时，原式＝2×（﹣）×3﹣4×（﹣）2﹣×32﹣＝﹣36．21．【解答】解：①由2x+3＝1，得x＝﹣1，当x＝﹣1时，代数式（2x+3）x+2020＝12019＝1；②由2x+3＝﹣1，得x＝﹣2，当x＝﹣2时，代数式（2x+3）x+2020＝（﹣1）2018＝1；③由x+2020＝0，得x＝﹣2020，当x＝﹣2020时，2x+3＝﹣4037≠0所以（2x+3）x+2020＝（﹣4037）0＝1．当x＝﹣2020时，代数式（2x+3）x+2020的值为1．答：当x为﹣1、﹣2、﹣2020时，代数式（2x+3）x+2020的值为1．22．【解答】解：（1）[（x﹣2y）2﹣4y2+2xy]÷2x＝[x2﹣4xy+4y2﹣4y2+2xy]÷2x＝[x2﹣2xy]÷2x＝，当x＝1，y＝2时，原式＝；（2）（﹣3ab）2（a2+ab+b2）﹣3ab（3a3b+3a2b2﹣ab3）＝9a2b2（a2+ab+b2）﹣（9a4b2+9a3b3﹣3a2b4）＝9a4b2+9a3b3+9a2b4﹣9a4b2﹣9a3b3+3a2b4＝12a2b4，当a＝，b＝时，原式＝．23．【解答】解：（1）原式＝a3﹣8；原式＝8x3﹣y3；（2）（a﹣b）（a2+ab+b2）＝a3﹣b3；（3）能⽤发现的乘法公式计算的是（4﹣x）（16+4x+x2）．故答案为：（1）a3﹣8；8x3﹣y3；（2）（a﹣b）（a2+ab+b2）＝a3﹣b3；（3）C．24．【解答】解：（1）图1中阴影部分的⾯积为：a2﹣b2，图2中阴影部分的⾯积为：（2b+2a）（a﹣b），即（a+b）（a﹣b）；故答案为：a2﹣b2，（a+b）（a﹣b）；（2）由图1与图2⾯积关系，可以得到⼀个等式：a2﹣b2＝（a+b）（a﹣b），故答案为：a2﹣b2＝（a+b）（a﹣b）；（3）∵a2﹣b2＝16，且a+b＝8，∴（a+b）（a﹣b）＝16，即8（a﹣b）＝16，∴a﹣b＝2．故答案为：2．。

浙教版七年级数学下册第三单元《整式的乘除》培优题一．选择题（共7小题）1．=（）A．1 B．C．2D．2．已知x m=a，x n=b（x≠0），则x3m﹣2n的值等于（）A．3a﹣2b B．a3﹣b2C．a3b2 D．3．根据图中数据，计算大长方形的面积，通过不同的计算方法，你发现的结论是（）A．（a+b）（a+2b）=a2+3ab+2b2B．（3a+b）（a+b）=3a2+4ab+b2C．（2a+b）（a+b）=2a2+3ab+b2D．（3a+2b）（a+b）=3a2+5ab+2b24．使（x2+px+8）（x2﹣3x+q）的乘积不含x3和x2，则p、q的值为（）A．p=0，q=0 B．p=﹣3，q=﹣1 C．p=3，q=1 D．p=﹣3，q=15．已知2a﹣b=2，那么代数式4a2﹣b2﹣4b的值是（）A．6 B．4 C．2 D．06．设0＜n＜m，m2+n2=4mn，则的值等于（）A．3 B．C．D．27．为了求1+2+22+23+…+22011+22012的值，可令S=1+2+22+23+…+22011+22012，则2S=2+22+23+24+…+22012+22013，因此2S﹣S=22013﹣1，所以1+22+23+…+22012=22013﹣1．仿照以上方法计算1+5+52+53+…+52012的值是（）A．52013﹣1 B．52013+1 C．D．8．若代数式x2+3x+2可以表示为（x﹣1）2+a（x﹣1）+b的形式，则a+b的值是．9．有足够多的长方形和正方形的卡片，如图．如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙）．（1）请画出如图这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．这个长方形的代数意义是．（2）小明想用类似的方法拼成了一个边长为a+3b和2a+b的矩形框来解释某一个乘法公式，那么小明需用2号卡片张，3号卡片张．10．4个数a，b，c，d排列成，我们称之为二阶行列式．规定它的运算法则为：=ad﹣bc．若=12，则x=．11．若x=2m﹣1，y=1+4m+1，用含x的代数式表示y为．12．若m1，m2，…m2015是从0，1，2这三个数中取值的一列数，若m1+m2+…+m2015=1525，（m1﹣1）2+（m2﹣1）2+…+（m2015﹣1）2=1510，则在m1，m2，…m2015中，取值为2的个数为．13．已知a是大于1的实数，且有a3+a﹣3=p，a3﹣a﹣3=q成立．（1）若p+q=4，求p﹣q的值；（2）当q2=22n+﹣2（n≥1，且n是整数）时，比较p与（a3+）的大小，并说明理由．14．归纳与猜想：（1）计算：①（x﹣1）（x+1）=；②（x﹣1）（x2+x+1）=；③（x﹣1）（x3+x2+x+1）=；（2）根据以上结果，写出下列各式的结果．①（x﹣1）（x6+x5+x4+x3+x2+x+1）=；②（x﹣1）（x9+x8+x7+x6+x5+x4+x3+x2+x+1）=；（3）（x﹣1）（x n﹣1+x n﹣2+x n﹣3+…+x2+x+1）=（n为整数）；（4）若（x﹣1）•m=x15﹣1，则m=；（5）根据猜想的规律，计算：226+225+…+2+1．15．杨辉三角形是一个由数字排列成的三角形数表，一般形式如图所示，其中每一横行都表示（a+b）n（此处n=0，1，2，3，4，5…）的计算结果中的各项系数．杨辉三角最本质的特征是，它的两条斜边都是数字1组成，而其余的数则是等于它“肩”上的两个数之和．（a+b）0=1（a+b）1=a+b（a+b）2=a2+2ab+b2（a+b）3=a3+3a2b+3ab2+b3（a+b）4=a4+4a3b+6a2b2+4ab3+b4（a+b）5=a5+5a4b+10a3b2+10a2b3+5ab4+b5…上面的构成规律聪明的你一定看懂了！（1）请直接写出（a+b）6的计算结果中a2b4项的系数是；（2）利用上述规律直接写出27=；杨辉三角还有另一个特征：（3）从第二行到第五行，每一行数字组成的数（如第三行为121）都是上一行的数与的积．（4）由此你可以写出115=．（5）由第行可写出118=．浙教版七年级数学下册第三单元《整式乘除》参考答案与试题解析一．选择题（共7小题）1．（2012秋•南陵县期末）=（）A．1 B．C．2D．【分析】根据x a•y a=（xy）a，进行运算即可．【解答】解：原式=（×）2004×=．故选B．【点评】此题考查了同底数幂的乘法运算，属于基础题，注意式子：x a•y a=（xy）a的运用．2．（2001•乌鲁木齐）已知x m=a，x n=b（x≠0），则x3m﹣2n的值等于（）A．3a﹣2b B．a3﹣b2C．a3b2 D．【分析】利用同底数幂的除法和幂的乘方的性质的逆运算计算即可．【解答】解：∵x m=a，x n=b（x≠0），∴x3m﹣2n=x3m÷x2n=．故选D．【点评】本题考查了同底数幂的除法，幂的乘方的性质，逆用性质是解题的关键．3．（2016春•苏州期中）根据图中数据，计算大长方形的面积，通过不同的计算方法，你发现的结论是（）A．（a+b）（a+2b）=a2+3ab+2b2B．（3a+b）（a+b）=3a2+4ab+b2C．（2a+b）（a+b）=2a2+3ab+b2D．（3a+2b）（a+b）=3a2+5ab+2b2【分析】大长方形的长为3a+2b，宽为a+b，表示出面积；也可以由三个边长为a的正方形，2个边长为b的正方形，以及5个长为b，宽为a的长方形面积之和表示，即可得到正确的选项．【解答】解：根据图形得：（3a+2b）（a+b）=3a2+5ab+2b2．故选：D．【点评】此题考查了多项式乘多项式，弄清题意是解本题的关键．4．（2016秋•简阳市期中）使（x2+px+8）（x2﹣3x+q）的乘积不含x3和x2，则p、q的值为（）A．p=0，q=0 B．p=﹣3，q=﹣1 C．p=3，q=1 D．p=﹣3，q=1【分析】根据多项式乘多项式的法则计算，然后根据不含x2项和x3项就是这两项的系数等于0列式，求出p和q的值，从而得出．【解答】解：（x2+px+8）（x2﹣3x+q），=x4+（p﹣3）x3+（8﹣3p+q）x2+（pq﹣24）x+8q，∵（x2+px+8）（x2﹣3x+q）的展开式中不含x2项和x3项，∴解得：．故选：C．【点评】本题考查了多项式乘多项式的运算法则，根据不含哪一项就是让这一项的系数等于0列式是解题的关键．5．（2015春•房山区期末）已知2a﹣b=2，那么代数式4a2﹣b2﹣4b的值是（）A．6 B．4 C．2 D．0【分析】根据完全平方公式，可得平方差公式，根据平方差公式，可得答案．【解答】解：4a2﹣b2﹣4b=4a2﹣（b2+4b+4）+4=（2a）2﹣（b+2）2+4=[2a+（b+2）][2a﹣（b+2）]+4=（2a+b+2）（2a﹣b﹣2）+4当2a﹣b=2时，原式=0+4=4，故选：B．【点评】本题考查了完全平方公式，利用完全平方公式得出平方差公式是解题关键．6．（2012•宁波模拟）设0＜n＜m，m2+n2=4mn，则的值等于（）A．3 B．C．D．2【分析】已知等式变形后利用完全平方公式化简得到关系式，代入所求式子计算即可得到结果．【解答】解：m2+n2=4mn变形得：（m﹣n）2=2mn，（m+n）2=6mn，∵0＜n＜m，∴m﹣n＞0，m+n＞0，∴m﹣n=，m+n=，∴原式===2．故选D．【点评】此题考查了完全平方公式，以及平方差公式，熟练掌握公式是解本题的关键．7．（2014•金水区校级模拟）为了求1+2+22+23+…+22011+22012的值，可令S=1+2+22+23+…+22011+22012，则2S=2+22+23+24+…+22012+22013，因此2S﹣S=22013﹣1，所以1+22+23+…+22012=22013﹣1．仿照以上方法计算1+5+52+53+…+52012的值是（）A．52013﹣1 B．52013+1 C．D．【分析】根据题目所给计算方法，令S=1+5+52+53+…+52012，再两边同时乘以5，求出5S，用5S﹣S，求出4S的值，进而求出S的值．【解答】解：令S=1+5+52+53+ (52012)则5S=5+52+53+…+52012+52013，5S﹣S=﹣1+52013，4S=52013﹣1，则S=．故选D．【点评】本题考查了同底数幂的乘法，利用错位相减法，消掉相关值，是解题的关键．二．填空题（共5小题）8．（2012•泰州）若代数式x2+3x+2可以表示为（x﹣1）2+a（x﹣1）+b的形式，则a+b的值是11．【分析】利用x2+3x+2=（x﹣1）2+a（x﹣1）+b，将原式进行化简，得出a，b的值，进而得出答案．【解答】解：∵x2+3x+2=（x﹣1）2+a（x﹣1）+b=x2+（a﹣2）x+（b﹣a+1），∴a﹣2=3，∴a=5，∵b﹣a+1=2，∴b﹣5+1=2，∴b=6，∴a+b=5+6=11，故答案为：11．【点评】此题主要考查了整式的混合运算与化简，根据已知得出x2+3x+2=x2+（a ﹣2）x+（b﹣a+1）是解题关键．9．（2012•杭州模拟）有足够多的长方形和正方形的卡片，如图．如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙）．（1）请画出如图这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．这个长方形的代数意义是a2+3ab+2b2=（a+b）（a+2b）．（2）小明想用类似的方法拼成了一个边长为a+3b和2a+b的矩形框来解释某一个乘法公式，那么小明需用2号卡片3张，3号卡片7张．【分析】（1）画出相关草图，表示出拼合前后的面积即可；（2）得到所给矩形的面积，看有几个b2，几个ab即可．【解答】解：（1）如图所示：故答案为：a2+3ab+2b2=（a+b）（a+2b）；（2）（a+3b）（2a+b）=2a2+ab+6ab+3b2=2a2+7ab+3b2，需用2号卡片3张，3号卡片7张．故答案为：a2+3ab+2b2=（a+b）（a+2b）；3；7．【点评】考查多项式与多项式相乘问题；根据面积的不同表示方法得到相应的等式是解决本题的关键．10．（2015•崇左）4个数a，b，c，d排列成，我们称之为二阶行列式．规定它的运算法则为：=ad﹣bc．若=12，则x=1．【分析】利用题中的新定义化简已知等式，求出解即可得到x的值．【解答】解：利用题中新定义得：（x+3）2﹣（x﹣3）2=12，整理得：12x=12，解得：x=1．故答案为：1．【点评】此题考查了整式的混合运算，弄清题中的新定义是解本题的关键．11．（2014春•苏州期末）若x=2m﹣1，y=1+4m+1，用含x的代数式表示y为y=4（x+1）2+1．【分析】将4m变形，转化为关于2m的形式，然后再代入整理即可【解答】解：∵4m+1=22m×4=（2m）2×4，x=2m﹣1，∴2m=x+1，∵y=1+4m+1，∴y=4（x+1）2+1，故答案为：y=4（x+1）2+1．【点评】本题考查幂的乘方的性质，解决本题的关键是利用幂的乘方的逆运算，把含m的项代换掉．12．（2015•雅安）若m1，m2，…m2015是从0，1，2这三个数中取值的一列数，若m1+m2+…+m2015=1525，（m1﹣1）2+（m2﹣1）2+…+（m2015﹣1）2=1510，则在m1，m2，…m2015中，取值为2的个数为510．【分析】通过m1，m2，…m2015是从0，1，2这三个数中取值的一列数，（m1﹣1）2+（m2﹣1）2+…+（m2015﹣1）2=1510从而得到1的个数，由m1+m2+…+m2015=1525得到2的个数．【解答】解：∵（m1﹣1）2+（m2﹣1）2+…+（m2015﹣1）2=1510，∵m1，m2，…，m2015是从0，1，2这三个数中取值的一列数，∴m1，m2，…，m2015中为1的个数是2015﹣1510=505，∵m1+m2+…+m2015=1525，∴2的个数为（1525﹣505）÷2=510个．故答案为：510．【点评】此题考查完全平方的性质，找出运算的规律．利用规律解决问题．三．解答题（共3小题）13．（2015秋•厦门期末）已知a是大于1的实数，且有a3+a﹣3=p，a3﹣a﹣3=q成立．（1）若p+q=4，求p﹣q的值；（2）当q2=22n+﹣2（n≥1，且n是整数）时，比较p与（a3+）的大小，并说明理由．【分析】（1）根据已知条件可得a3=2，代入可求p﹣q的值；（2）根据作差法得到p﹣（a3+）=2﹣n﹣，分三种情况：当n=1时；当n=2时；当n≥3时进行讨论即可求解．【解答】解：（1）∵a3+a﹣3=p①，a3﹣a﹣3=q②，∴①+②得，2a3=p+q=4，∴a3=2；①﹣②得，p﹣q=2a﹣3==1．（2）∵q2=22n+﹣2（n≥1，且n是整数），∴q2=（2n﹣2﹣n）2，∴q2=22n+2﹣2n，又由（1）中①+②得2a3=p+q，a3=（p+q），①﹣②得2a﹣3=p﹣q，a﹣3=（p﹣q），∴p2﹣q2=4，p2=q2+4=（2n+2﹣n）2，∴p=2n+2﹣n，∴a3+a﹣3=2n+2﹣n③，a3﹣a﹣3=2n﹣2﹣n④，∴③+④得2a3=2×2n，∴a3=2n，∴p﹣（a3+）=2n+2﹣n﹣2n﹣=2﹣n﹣，当n=1时，p＞a3+；当n=2时，p=a3+；当n≥3时，p＜a3+．【点评】考查了负整数指数幂：a﹣p=（a≠0，p为正整数），关键是加减消元法和作差法的熟练掌握．14．归纳与猜想：（1）计算：①（x﹣1）（x+1）=x2﹣1；②（x﹣1）（x2+x+1）=x3﹣1；③（x﹣1）（x3+x2+x+1）=x4﹣1；（2）根据以上结果，写出下列各式的结果．①（x﹣1）（x6+x5+x4+x3+x2+x+1）=x7﹣1；②（x﹣1）（x9+x8+x7+x6+x5+x4+x3+x2+x+1）=x10﹣1；（3）（x﹣1）（x n﹣1+x n﹣2+x n﹣3+…+x2+x+1）=x n﹣1（n为整数）；（4）若（x﹣1）•m=x15﹣1，则m=x14+x13+x12+…+x2+x+1；（5）根据猜想的规律，计算：226+225+…+2+1．【分析】（1）运用乘法公式以及多项式乘多项式的法进行计算即可；（2）根据（1）中的计算结果的变换规律进行判断即可；（3）根据（1）（2）中的计算结果总结变换规律即可；（4）根据（3）中的规律，直接求得m的表达式即可；（5）根据（3）中的规律列出等式进行变形，求得226+225+…+2+1的值．【解答】解：（1）①（x﹣1）（x+1）=x2﹣1；②（x﹣1）（x2+x+1）=x3﹣1；③（x﹣1）（x3+x2+x+1）=x4+x3+x2+x﹣x3﹣x2﹣1=x4﹣1；（2）①（x﹣1）（x6+x5+x4+x3+x2+x+1）=x7﹣1；②（x﹣1）（x9+x8+x7+x6+x5+x4+x3+x2+x+1）=x10﹣1；（3）（x﹣1）（x n﹣1+x n﹣2+x n﹣3+…+x2+x+1）=x n﹣1（n为整数）；（4）∵（x﹣1）•m=x15﹣1，∴m=x14+x13+x12+…+x2+x+1；（5）∵（2﹣1）（226+225+224+…+22+2+1）=227﹣1，∴226+225+…+2+1=227﹣1．【点评】本题主要考查了多项式与多项式相乘的法则：多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．计算时按一定的顺序进行，必须做到不重不漏．15．（2014春•泰兴市校级期末）杨辉三角形是一个由数字排列成的三角形数表，一般形式如图所示，其中每一横行都表示（a+b）n（此处n=0，1，2，3，4，5…）的计算结果中的各项系数．杨辉三角最本质的特征是，它的两条斜边都是数字1组成，而其余的数则是等于它“肩”上的两个数之和．（a+b）0=1（a+b）1=a+b（a+b）2=a2+2ab+b2（a+b）3=a3+3a2b+3ab2+b3（a+b）4=a4+4a3b+6a2b2+4ab3+b4（a+b）5=a5+5a4b+10a3b2+10a2b3+5ab4+b5…上面的构成规律聪明的你一定看懂了！（1）请直接写出（a+b）6的计算结果中a2b4项的系数是15；（2）利用上述规律直接写出27=128；杨辉三角还有另一个特征：（3）从第二行到第五行，每一行数字组成的数（如第三行为121）都是上一行的数与11的积．（4）由此你可以写出115=161051．（5）由第9行可写出118=214358881．【分析】观察图表寻找规律：三角形是一个由数字排列成的三角形数表，它的两条斜边都是数字1组成，而其余的数则是等于它“肩”上的两个数之和．【解答】解：（1）请直接写出（a+b）6的计算结果中a2b4项的系数是15；（2）利用上述规律直接写出27=128；杨辉三角还有另一个特征：（3）从第二行到第五行，每一行数字组成的数（如第三行为121）都是上一行的数与11的积．（4）由此你可以写出115=161051．（5）由第9行可写出118=214358881．故答案为：15，128，11，161051，9，214358881．【点评】考查了学生解决实际问题的能力和阅读理解能力，找出本题的数字规律是正确解题的关键．。

专题：B 卷得分能力提升一、填空题（代数类）1、已知：1052==b a ，则b a 11+的值为 2、已知：102558111===z y x ，则z y x ++=3、已知：1284212=⋅+y x ，则y x +=4、已知：53=a ，109=b ，则b a 23-=5、已知：25102=y ，则y -10=6、已知：)3)(8(22b x x ax x +-++的乘积中不含2x 和3x 项，则a = ，b = 7、若)1)(12(+-=a a M ，)1)(4(-+=a a N ，则M 、N 的大小关系为8、已知a 、b 满足522+=b a ，则33)()(b a b a -+= 9、若20)63(2)3(----a a 有意义，则a 的取值范围10、已知：36)2(2+--x m x 是完全平方式，则m= 11、已知：102622-=-+x y y x ，则y x -= 12、已知：01461322=+-+-x y xy x ，则20162017)(x y x +=13、若201742222++++=b a b a P ，则P 的最小值是= 14、已知201620181201720181201820181222+=+=+=x c x b x a ，，， 则ac bc ab c b a ---++222的值为15、已知（a －1）（b －2）－a （b －3）＝3，则代数式222b a +－ab 的值为 16、已知2017)2018)(2016(=--a a ，则22)2018()2016(a a -+-= 17、已知5=+b a ，3=ab ，则2)(b a -=18、已知：01223344555)1(a x a x a x a x a x a x +++++=+，则135a a a ++= 19、已知51=-xx ，则142+x x = 20、已知：0132=--x x ，则221x x += ，441x x += 20、已知：n mx x x +++2394能被322-+x x 整除，则n m -的值为 21、已知：099052=-+x x ，则代数式1027985623+-+x x x 的值为 22、计算：)201711()411)(311)(211(2222---- = 23、计算31164221)211()211)(211)(211(+++++ = 24、1)12()12)(12)(12(6442+++++ 的各位数字是二、填空题（几何类） 1、已知一个角的两边与另一个角的两边分别平行，则这两个角的数量关系是2、已知一个角的补角比这个角的余角的3倍大10度，则这个角的余角的度数为3、将一个直角三角板和一把直尺如图放置，如果∠α=43°，则∠β的度数是4、如图，已知AE ∥BD ，∠1=3∠2，∠2=25°，则∠C=（第3题图） （第4题图） （第5题图） （第6题图）5、如图，AB ∥EF ∥CD ，∠ABC=46°，∠CEF=154°，则∠BCE 等于6、如图，l ∥m ，等腰直角三角形ABC 的直角顶点C 在直线m 上，若∠β=20°，则∠α的度数为7、如图，已知AB ∥EF ∥CD ，EG 平分∠BEF ，∠B+∠BED+∠D =192°，∠B -∠D=24°，则∠GEF 的度数为（第7题图） （第8题图）（第9题图） （第10题图）8、如图，已知FD ∥BE ，则∠1+∠2-∠3=9、如图，12//l l ，∠1=120°，∠2=100°，则∠3=10、如图，1502110AB CD ∠=∠=∥，°，°，则3∠= 三、解答题1、图（1）是一个长为2m 、宽为2n 的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图（2）的形状拼成一个正方形．（1）你认为图（2）中阴影部分的正方形的边长等于多少？ ；（2）请用两种不同的方法求图（2）中阴影部分面积．方法一： ；方法二： ；（3）观察图（2），你能写出下列三个代数式之间的等量关系吗？代数式：（m+n ）2，（m ﹣n ）2，4mn ． ；（4）根据（3）题中的等量关系，解决如下问题：若a+b=7，ab=5，求（a ﹣b ）2的值．2、（1）、填空：))((b a b a +-=))((22b ab a b a ++-=))((2222b ab b a a b a +++-=（2）、猜想：))((1221---++++--n n n b ab b a a b a n = （其中n 为正整数，且n ≥2）（3）、利用（2）猜想的结论计算：22222223789+-+-+-3、如图，已知l1∥l2，MN分别和直线l1、l2交于点A、B，ME分别和直线l1、l2交于点C、D，点P在MN上（P点与A、B、M三点不重合）．（1）如果点P在A、B两点之间运动时，∠α、∠β、∠γ之间有何数量关系请说明理由；（2）如果点P在A、B两点外侧运动时，∠α、∠β、∠γ有何数量关系（只须写出结论）．4、如图3个图中，均有AB∥CD，（1）如图1，点P为AB、CD间的一个折点，则∠1、∠2、∠3的关系是___________；（2）如图2，在（1）的基础上增加一个折点，则∠1、∠2、∠3、∠4的关系是___________；（3）如图3，当AB、CD间有三个折点时，则∠1、∠2、∠3、∠4、∠5的关系是___________；（4）通过以上4题的探究，从中寻找规律，并解答，当AB、CD间有n个折点时，则∠1、∠2、……∠n+2之间的关系是____________________________________。

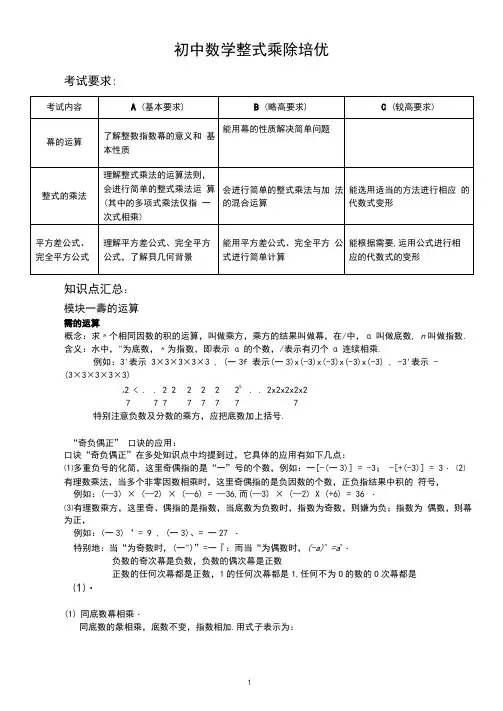
初中数学整式乘除培优考试要求:知识点汇总：模块一壽的运算需的运算概念：求〃个相同因数的积的运算，叫做乘方，乘方的结果叫做幕，在/中，α叫做底数, n叫做指数. 含义：水中，"为底数，〃为指数，即表示α的个数，/表示有刃个α连续相乘.例如：3'表示3×3×3×3×3 , (一3f 表示(一3)x(-3)x(-3)x(-3)x(-3) , -3'表示 -(3×3×3×3×3)5. . 2x2x2x2x2z2 < . . 2 2 2 2 2 27 7 7 7 7 7 7 7特别注意负数及分数的乘方，应把底数加上括号.“奇负偶正” 口诀的应用：口诀“奇负偶正”在多处知识点中均提到过，它具体的应用有如下几点：⑴多重负号的化简，这里奇偶指的是“一”号的个数，例如：一[-(一3)] = -3； -[+(-3)] = 3・⑵有理数乘法，当多个非零因数相乘时，这里奇偶指的是负因数的个数，正负指结果中积的符号，例如：(—3) × (—2) × (—6) = —36,而(—3) × (—2) X (+6) = 36 ・⑶有理数乘方，这里奇、偶指的是指数，当底数为负数时，指数为奇数，则嫌为负；指数为偶数，则幕为正，例如：(一3)‘ = 9 , (一3)、= 一27 ・特别地：当“为奇数时，(一")”=一『：而当“为偶数时，(-a)n =a n・负数的奇次幕是负数，负数的偶次幕是正数正数的任何次幕都是正数，1的任何次幕都是1,任何不为O的数的O次幕都是⑴・(1)同底数幕相乘・同底数的彖相乘，底数不变，指数相加.用式子表示为：(m√ι都是正整数)・(2) 策的乘方.幕的乘方的运算性质：幕的乘方.底数不变，指数相乘.用式子麦示为: (町=旷(m 9n 都是正整数)・ ⑶积的乘方.积的乘方的运算性质：积的乘方，等于把积的每一个因式分别乘方，再把所得的無相乘•用 式子表示为： (ab)n ≈a fl h fl(“是正整数)・ (4)同底数彖相除・同底数的幕相除，底数不变，指数相减.用式子表示为:模块二整式的乘法⑴单项式与单项式相乘：系数、同底数幕分别相乘作为积的因式，只有一个单项式里含有的 字母，则连同它的指数作为积的一个因式・以下举例说明单项式与单项式相乘的规则如下：Ub • 3a 2b y c 2= 3a^c 2,两个单项式的系数分 别为1和3,乘积的系数是3,两个单项式中关于字母α的幕分别是α和/,乘积中d 的幕 是才,同理，乘积中b 的幕是戻，另外，单项式“b 中不含C 的幕，而3i l 2b i c 2中含¢2,故乘 积中含疋・ ⑵单项式与多项式相乘：单项式分别与多项式中的每一项相乘，然后把所得的积相加，公式为：m(a + b + c) = ma + mb + me ,其中加为单项式，a+b + c为 多项式.⑶多项式与多项式相乘:将一个多项式中的每一个单项式分别与另一个多项式中的每一个单 项式相乘，然后把积相加，公式为：(∕π + n)(a + b) = ma + mb + Ha + Hh模块三整式的除法(1) 单项式除以单项式^系数、同底数的幕分别相除作为商的因式，对于只在被除式中含有 的字母，則连同它的指数作为商的一个因式•如：3a 2b 3c 2*ab = 3ab 2c 2,被除式为3a 2b 3c 2, 除式为肪，系数分别为3和1,故商中的系数为3, α的彖分别为/和α,故商中α的 幕为∕τ=α,同理，〃的幕为，，另外，被除式中含Y,而除式中不含关于c ・的策，故 商中e 的幕为c'・(2) 多项式除以单项式：多项式中的每一项分别除以单项式，然后把所得的商相加， 公式为：(" + b + c ∙)÷∙m = "*"2 + b*m + c*"?,其中加为单项式，a + h + c 为多项式.(3) 多项式除以多项式后有专题介绍.模块四平方差公式(a+ h){a-b) = a 2 -h 2平方差公式的特点：即两数和与它们差的积等于这两数的平方差。

北师大版七年级数学下册第一章：整式的乘除—计算专题培优训练一、计算题1．计算：（1）(a 3)3·(a 4)3；（2）(－a 2)3·(b 3)2·(ab)4.（3）(3x －1)(2x －1)；（4）5x(x ＋1)2－(2x ＋3)(2x －3)．2．计算：（1）（﹣2a 2b ）3+8（a 2）2•（﹣a ）2•（﹣b ）3；（2）（x﹣3）0﹣（）﹣2+（﹣1）2021+|﹣5|．123．计算：（1）x 3y 2··．23(32xy 2)2(23x )（2）；[(−a 5)4÷a 12]2⋅(−2a 4)4．要求：利用乘法公式计算（1）2023×2021−20222（2）(2x−y +3)(2x−y−3)5．计算：（1）；(−2022)0−(12)−2+(−2)3（2）．(3a−b)2−(a−3b)(a +3b)6．计算：（1）；(π−2)0−(12)−2+32（2）．(−2x 2)2+x 3⋅x−x 5÷x 7．计算：（1）(π−3)0+(12)−2×2−1（2）2x 2⋅x 4+(−2x 2)3−x 7÷x8．计算：（1）；(3−π)0+(−13)−3+(−3)3÷(−3)2（2） .(x−2)2−(x−1)(x +3)9．计算：（1）(12)−1+(π−3.14)0−(−1)2022（2）(−2x 2)3+x 2⋅x 4+(−3x 3)210．计算：（1）；(2022−π)0−32+(12)−3（2）．m 2⋅m 6−(2m 2)4+m 9÷m 11．计算（1）．15x 5(y 4z)2÷(−3x 4y 5z 2)（2）．(x +1)(x−1)+x(2−x)12．计算：（1）(−2a 2bc 4)3（2）3x 2−x 6÷x 4（3）[−8a 2b 3+6ab 2−(−2ab)]÷(−2ab)（4）6x 2−2(2x−3)(4x +1)（5）(a +2b)2−(a−2b)2+(a +b)(a−b)13．计算：（1）；−42⋅(−12)3−(−1)202（2）．[(3xy +1)(3xy−1)+(xy−1)2]÷2xy 14．化简：．[(2a +b)(2a−b)−4(a−b)2−b 2]÷(−2b )15．化简：．[(x−y)(x +y)+(3x−y)2]÷2x 16．计算：（1） ．(2m 3)⋅(3m 2p)÷(2mp)（2） ．(a +1)2+(a +3)(a−3)17．计算：（1）（﹣x 2y 5）•（xy ）3；（2）（a 2﹣b 2）2+2a （ab﹣1）.18．计算：（1）a 5·（﹣a ）4﹣（﹣a 3）3；（2）20210+（）﹣1；13（3）（15x 2y﹣10xy 2）÷5xy ．（4）x （x﹣3）﹣（x﹣1）（x+2）．（1）已知：＝5，＝3，计算的值．4m 8n 22m +3n （2）已知：3x+5y ＝8，求的值．8x ⋅32y 20．计算：（1）；|−2|−(2−π)0+(13)−1（2）；(3x 2)2⋅(−4y 3)÷(6xy)2（3）（简便运算）；1032−102×104（4）．[(2x−y)(2x +y)+y(y−6x)]÷2x 21．计算：（1）；(x−3)(x +2)（2）；(3+a )(3−a )（3）；a 3⋅a 4⋅a +(a 2)4+(−2a 4)2（4）．(a +b )2−b (2a +b )22．计算题：（1）(−13)−1+(−2)2+(π−2015)0（2）(4x 3y−6x 2y 2+2xy )÷(−2xy )（3）(2a 2b )3⋅(−7ab 2)÷14a 4b 3（4）（用简便方法计算）20152−2014×2016（5）(x +2)2−(x +1)(x−1)（6）（2a-b+3）（2a+b-3）（1）2-3÷＋（﹣）2；1212（2）（﹣2x 3y ）2·（﹣3xy 2）÷（6x 4y 3）；（3）（2x ＋1）（2x﹣1）＋（x ＋2）2；（4）20212﹣2020×202224．计算或化简：（1）(−x 2)3⋅x 4（2）(13)2022×(−3)2021（3）(m +1)2−(m +1)(m−1)+2m(m−1)（4）(a 4−8a 2+16)÷(a 2+4a +4)25．计算（1）x 5•（-2x ）3+x 9÷x 2•x-（3x 4）2（2）（2a-3b ）2-4a （a-2b ）（3）（3x-y ）2（3x+y ）2（4）（2a-b+5）（2a+b-5）26．计算：（1）4mn 2 （2m+3n －n 2）；（2）（3m + 4n ） 2－（3m －4n ）2；（3）（6a 3b 2－3a 2b 2+9a 2b ）（－3a 2b ）；÷（4）（-8）2020 ×（-0.125）2021．（1）3x(2x−3)（2）（a+b ）（3a-2b ）（3）（4a 2-6ab+2a ）÷2a（4）20192-2017×2021（用乘法公式）28．计算：（1）；(−34)2021×(−43)2022（2）；(−2a 2)3⋅a 2−3a 11÷a 3（3）.(x +2y−3)(x−2y−3)29．计算：（1）2a （3a ＋2）；（2）（4m 3﹣2m 2）÷（﹣2m ）；（3）（x ＋2）（x﹣2）﹣（x﹣2）2；（4）．(π−3)0+(−12)−2−21+(−1)202130．算一算：（1）3m 2⋅m 8−(m 2)2⋅(m 3)2（2）[(a 5)3⋅(b 3)2]5（3）−t 3⋅(−t)4⋅(−t)5（4）已知，求的值.2x +3y−3=09x ⋅27y （5）已知，求x 的值.2×8x ×16=223（1）a 2⋅a 4+(−a 2)3（2）(a 2)3⋅(a 2)4⋅(−a 2)5（3）(−2a 2b 3)4+(−a)8⋅(2b 4)3（4）−t 3⋅(−t)4⋅(−t)5（5）(p−q)4⋅(q−p)3⋅(p−q)2（6）(−3a)3−(−a)⋅(−3a)232．化简：（1）；(x 2)3⋅x 3−(−x)2⋅x 9÷x 2（2）（m﹣n ）（m+n ）﹣m （m﹣n ）；（3）；(3a +2b)2−(2a−3b)2（4）.[(2x +y)2−(3x−y)(3x +y)−2y 2]÷(−12x)33．计算：（1）35×(−3)3×(−3)2（2）−x 11÷(−x)6⋅(−x)5（3）y 3⋅y 3+(−2y 3)2（4）(3x 2y−xy 2+2xy)÷xy34．计算：（1）(−x)(−x)5+(x 2)3；（2） ；2x 3(−x)2−(−x 2)2×(−3x)（3） ；(−4x−3y 2)(3y 2−4x)（4） .(2x−y)2⋅(2x +y)235．计算.（1）（-）9÷（-）5；1313（2）（-a ）10÷（-a ）3；（3）（2a ）7÷（2a ）4；（4）a 19÷（a 12÷a 3）；（5）（-）6÷（-）2；1414（6）（-x-y ）6÷（x+y ）4.36．计算.（1）a 2·（ab ）3；（2）（ab ）3·（ac ）4；（3）a 5·（-a ）3+（-2a 2）4；（4）（-2x 2）3+x 2·x 4-（-3x 3）237．逆用积的乘方公式计算.（1）（）2022·（-1.25）2022；45（2）（-4）3×（-）3×（-）33413（3）（3）12×（）11x （-2）318825（4）（）100×（1）100x （）2021x4202223121438．计算.（1）（-5a 2b 3）（-3a ）（2）6a 2x 5·（-3a 3b 2x 2）（3）（-a 2b ）3·（-3ab 3）413（4）（-3a n+2b ）3·（-4ab n+3）2（5）（ab 2-2ab ）·ab2312（6）-2x·（x 2y+3y-1）1239．计算.（1）20170+2-2-（）2+2017；12（2）（-2ab ）（3a 2-2ab-b 2）；（3）（2a+3b ）2-（2a-b ）（2a+b ）；（4）（9x 2y-6xy 2+3xy ）÷（）40．计算.（1）x 3·（2x 3）2÷（x 4）2；（2）（a 4）3÷a 6÷（-a ）3；（3）（-x ）3÷x·（-x ）2；（4）-102n ×100÷（-10）2n-1.41．计算（1）(−x 2y)3÷(−13xy 3)（2）(−14x−3y)(−14x+3y)（3）(3x−1)(x+2)+(x−3)2（4）(a−b)3÷(a−b)+2ab 42．计算.（1）102×105（2）x·x5x7·（3）a2·（-a）4（4）x2m+1·x m43．计算（1）a2⋅a3（2）(y2)3⋅y2（3）(−15x2y3)3−x6y4（4） .(x−y)8÷(y−x)5⋅(y−x)2二、解答题44．已知，，求代数式的值．(a+b)2=5ab=−2(a−b)245．计算：已知(x+y)2=1，(x-y)2=49，求x2+y2和xy的值．46．已知：，求2xy的值．x2+y2=25， x+y=747．已知（a+b）2＝25，（a﹣b）2＝9．求a2﹣6ab+b2．48．已知a+b=3，ab=2，求①；②的值a2+b2a2+b2−ab 49．①已知a m=2，a n=3，求a m+2n的值。

培优训练(一)(30分钟 50分)一、选择题(每小题4分，共12分)1.(2014·南通中考)计算(－x )2·x 3的结果是( )(A )x 5 (B )－x 5 (C )x 6 (D )－x 62.已知n 是大于1的自然数，则(－c )n －1·(－c )n +1等于( )(A )()2n 1c -- (B )－2nc (C )－c 2n (D )c 2n3.(2014·滨州中考)求1+2+22+23+…+22 012的值，可令S =1+2+22+23+…+22 012，则2S =2+22+23+24+…+22 013，因此2S －S =22 013－1.仿照以上推理，计算出1+5+52+53+…+52 012的值为( )(A )52 012－1 (B )52 013－1 (C )2 013514- (D )2 012514- 二、填空题(每小题4分，共12分)4.已知4m +1=28,则4m =______.5.居里夫人发现了镭这种放射性元素.1千克镭完全衰变后，放出的热量相当于375 000千克煤燃烧所放出的热量.估计地壳内含有100亿千克镭，这些镭完全衰变后所放出的热量相当于______千克煤燃烧所放出的热量(用科学记数法表示).6.已知2x ·2x ·8=212，则x =_____.三、解答题(共26分)7.(8分)计算：(1)(－3)3·(－3)4·(－3); (2)a 3·a 2－a ·(－a )2·a 2;(3)(2m －n )4·(n －2m )3·(2m －n )6.8.(8分)已知a x=5,a y=4，求下列各式的值：(1)a x+2. (2)a x+y+1.【拓展延伸】9.(10分)化简：(1)(－2)n+(－2)n·(－2)(n为正整数). (2)(－x)2n－1·(－x)n+2(n为正整数).培优训练(二)(30分钟50分)一、选择题(每小题4分，共12分)1.(2014·重庆中考)计算(ab)2的结果是( )(A)2ab(B)a2b(C)a2b2 (D)ab22.下列运算中，正确的是( )(A)3a2－a2=2 (B)(－a2b) 3=a6b3(C)a3·a6=a9 (D)(2a2)2=2a43.已知一个正方体的棱长为2×102毫米，则这个正方体的体积为( )(A)6×106立方毫米(B)8×106立方毫米(C)2×106立方毫米(D)8×105立方毫米二、填空题(每小题4分，共12分)4.已知22×83=2n，则n的值为______.5.若2x+y=3，则4x×2y=______.6.计算：(1)［(56)6×(－65)6］7=________.(2)82 013× (－2 012=______.三、解答题(共26分)7.(8分)已知x－y=a，试求(x－y)3·(2x－2y)3·(3x－3y)3的值.8.(8分)比较3555，4444，5333的大小.【拓展延伸】9.(10分)阅读材料：一般地，如果a(a＞0，且a≠1)的b次幂等于N，那么数b叫做以a为底N的对数，记作log a N=b.例如，因为54=625，所以log5625=4；因为32=9，所以log39=2.对数有如下性质：如果a＞0，且a≠1，M＞0，N＞0，那么log a(MN)=log a M+log a N. 完成下列各题(1)因为______，所以log28=_______；(2)因为______，所以log216=______；(3)计算：log2(8×16)=_______+_______=_______.培优训练(三)(30分钟50分)一、选择题(每小题4分，共12分)1.(2014·江西中考)下列运算正确的是( )(A)a3+a3=2a6 (B)a6÷a－3=a3(C)a3·a3=2a3 (D)(－2a2)3=－8a62.和3－2的结果相同的数是( )(A)－6 (B)9的相反数(C)9的绝对值(D)9的倒数3.(2014·东营中考)若3x=4，9y=7，则3x－2y的值为( )(A)47(B)74(C)－3 (D)27二、填空题(每小题4分，共12分)4.(2014·滨州中考)根据你学习的数学知识，写出一个运算结果为a6的算式_____.5.根据里氏震级的定义，地震所释放的相对能量E与地震级数n的关系为：E=10n，那么9级地震所释放的相对能量是7级地震所释放的相对能量的______倍.6.计算：a－1·a－2÷a－3=_____.三、解答题(共26分)7.(8分)用小数或分数表示下列各数：(1)4－3×2 0130；(2)×10－3.8.(8分)小丽在学习了“除零以外的任何数的零次幂的值为1”后，遇到这样一道题：“如果(x－2)x+3=1，求x的值”，她解答出来的结果为x=－3.老师说她考虑的问题不够全面，你能帮助小丽解答这个问题吗？【拓展延伸】9.(10分)(1)通过计算比较下列各式中两数的大小：(填“＞”“＜”或“=”).①1－2 _____ 2－1;②2－3_____3－2;③3－4_____4－3;④4－5_____5－4;….(2)由(1)可以猜测n－(n+1)与(n+1)－n(n为正整数)的大小关系：当n______时，n－(n+1)＞(n+1)－n;当n______时，n－(n+1)<(n+1)－n.培优训练(四)(30分钟50分)一、选择题(每小题4分，共12分)1.某种细胞的直径是5×10－4毫米，这个数是( )(A)毫米(B)毫米(C) 5毫米(D) 05毫米2.(2014·大庆中考)科学家测得肥皂泡的厚度约为000 7米，用科学记数法表示为( )(A)×10－6米(B)×10－7米(C)7×10－7米(D)7×10－6米3.小聪在用科学记数法记录一个较小的数时，多数了2个零，结果错误地记成×10－8，正确的结果应是( )(A)×106 (B)×10－6(C)×1010 (D)×10－10二、填空题(每小题4分，共12分)4.(2014·玉林中考)某种原子直径为×10－2纳米，把这个数化为小数是_____纳米.5.(2014·本溪中考)已知1纳米=10－9米，某种微粒的直径为158纳米，用科学记数法表示该微粒的直径为_____.本100页的书大约厚cm,则书的一页厚约______ m(用科学记数法表示).三、解答题(共26分)7.(8分)某种计算机的存储器完成一次存储的时间为十亿分之一秒,则该存储器用百万分之一秒可以完成多少次存储?8.(8分)在显微镜下，人体的一种细胞形状可以近似地看成圆形，它的半径为×10－7米，它相当于多少微米？若1张百元人民币约09米厚，那么它相当于约多少个这种细胞首尾相接的长度？【拓展延伸】9.(10分)1微米相当于一根头发直径的六十分之一,一根头发的直径大约为多少米? 一根头发的横断面的面积为多少平方米？一般人约有10万根头发,把这些头发捆起来的横断面约有多少平方米(π取?培优训练(五)(30分钟50分)一、选择题(每小题4分，共12分)1.(2014·沈阳中考)计算(2a)3·a2的结果是( )(A)2a5 (B)2a6 (C)8a5 (D)8a62.下列运算正确的是( )(A)|－3|=3 (B)－(－12)=－12(C)(a3)2=a5(D)2a·3a=6a3.如果－2m2×□=－8m2n3,则□内应填的代数式是( )(A)6n3 (B)4n3(C)－6n3 (D)4m2n3二、填空题(每小题4分，共12分)4.计算：(－2x) 3·(－5xy2)=______.5.已知x m+1y n－2·x m y2=x5y3，那么m n的值是______.6.如图，沿正方形的对角线对折，把对折后重合的两个小正方形内的单项式相乘，乘积是_____(只要求写出一个结论).三、解答题(共26分)7.(8分)若1+2+3+…+n=m，求(ab n)·(a2b n－1)…(a n－1b2)·(a n b)的值.8.(8分)用18个棱长为a的正方体木块拼成一个长方体，有几种不同的拼法，分别表示你所拼成的长方体的体积，不同的拼法中，你能得到什么结论(至少用两种方法)？【拓展延伸】9.(10分)已知三角表示2ab c，方框表示(－3x z w)y，求×.培优训练(六)(30分钟50分)一、选择题(每小题4分，共12分)1.今天数学课上，老师讲了单项式乘以多项式，放学后，小华回到家拿出课堂笔记，认真复习老师课上讲的内容，他突然发现一道题：－3xy·(4y－2x－1)=－12xy2+6x2y+_____.空格的地方被钢笔水弄污了，你认为横线上应填写( )(A)3xy(B)－3xy(C)－1 (D)12.要使(x2+ax+1)(－6x3)的展开式中不含x4的项，则a应等于( )(D)0(A)6 (B)－1 (C)16(－a+b－c)与－a(a2－ab+ac)的关系是( )(A)相等(B)互为相反数C)前式是后式的－a倍D)前式是后式的a倍二、填空题(每小题4分，共12分)4.计算：－2a(b2+ab)+(a2+b)b= _______ .5.若2x(x－1)－x(2x+3)=15，则x=_____.6.如图所示图形的面积可表示的代数恒等式是______.三、解答题(共26分)7.(8分)某同学在计算一个多项式乘以－3x2时，因抄错运算符号，算成了加上－3x2，得到的结果是x2－4x+1，那么正确的计算结果是多少？8.(8分)已知某长方形的长为(a+b)cm，它的宽比长短(a－b)cm，求这个长方形的周长与面积.【拓展延伸】a米.9.(10分)一条防洪堤坝，其横断面是梯形，上底宽a米，下底宽(a+2b)米，坝高12(1)求防洪堤坝的横断面面积；(2)如果防洪堤坝长100米，那么这段防洪堤坝的体积是多少立方米？培优训练(七)(30分钟50分)一、选择题(每小题4分，共12分)1.下列计算中，正确的有( )①(2a－3)(3a－1)=6a2－11a+3; ②(m+n)(n+m)=m2+mn+n2;③(a－2)(a+3)=a2－6; ④(1－a)(1+a)=1－a2.(A)4个(B)3个(C)2个(D)1个2.已知(x+a)(x+b)=x2－13x+36，则a+b的值是( )(A)13 (B)－13 (C)36 (D)－363.一个三角形的一边长为m+2，这条边上的高比它长m，则这个三角形的面积为( )(A)2m2+6m+4 (B)m2+3m+2 (C)m+2 (D)1m+12二、填空题(每小题4分，共12分)4.已知a2－a+5=0，则(a－3)(a+2)的值是_____.5.将一个长为x、宽为y的长方形的长增加1、宽减少1得到的新长方形的面积是_____.6.有若干张如图所示的A类、B类正方形卡片和C类长方形卡片，如果要拼成一个长为3a+b，宽为a+2b的大长方形，则需要C类卡片_____张.三、解答题(共26分)7.(8分)说明：对于任意的正整数n，代数式n(n+7)－(n+3)(n－2)的值总能被6整除.8.(8分)如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a(a+b)=a2+ab成立.(1)根据图乙，利用面积的不同表示方法，写出一个代数恒等式______；(2)试写出一个与(1)中代数恒等式类似的等式，并用上述拼图的方法说明它的正确性. 【拓展延伸】9.(10分)观察下列等式：12×231=132×21，13×341=143×31，23×352=253×32，34×473=374×43，62×286=682×26，……以上每个等式中两边数字是分别对称的，且每个等式中组成两位数与三位数的数字之间具有相同规律，我们称这类等式为“数字对称等式”.(1)根据上述各式反映的规律填空，使式子成为“数字对称等式”：①52×_____=_____×25；②_____×396=693×_____.(2)设这类等式左边两位数的十位数字为a，个位数字为b，且2≤a+b≤9，写出表示“数字对称等式”一般规律的式子(含a，b)，并说明其正确性.培优训练(八)(30分钟50分)一、选择题(每小题4分，共12分)1.计算(3a－b)(－3a－b)等于( )(A)9a2－6ab－b2 (B)－9a2－6ab－b2(C)b2－9a2 (D)9a2－b22.由m(a+b+c)=ma+mb+mc①，可得：(a+b)(a2－ab+b2)=a3－a2b+ab2+a2b－ab2+b3=a3+b3，即(a+b)(a2－ab+b2)=a3+b3②.我们把等式②叫做多项式乘法的立方公式.下列应用这个立方公式进行的变形不正确的是( )(A)(x+4y)(x2－4xy+16y2)=x3+64y3(B)(2x+y)(4x2－2xy+y2)=8x3+y3(C)(a+1)(a2＋a+1)=a3+1 (D)x3+27=(x+3)(x2－3x+9)3.下列各式中，计算结果为81－x2的是( )(A)(x+9)(x－9) (B)(x+9)(－x－9) (C)(－x+9)(－x－9) (D)(－x－9)(x－9)二、填空题(每小题4分，共12分)4.当x=3，y=1时，代数式(x+y)(x－y)+y2的值是______.5.如果(a+b+1)(a+b－1)=63，那么a+b的值为______.6.观察下列各式：(x－1)(x+1)=x2－1，(x－1)(x2+x+1)=x3－1，(x－1)(x3+x2+x+1)=x4－1，根据前面各式的规律可得(x－1)(x n+x n－1+…+x+1)=_____(其中n为正整数).三、解答题(共26分)7.(8分)a，b，c是三个连续的正整数(a＜b＜c)，以b为边长作正方形，分别以c，a为长和宽作长方形，哪个图形的面积大？为什么？8.(8分)如图所示，小明家有一块L型的菜地，要把L型的菜地按图中所示的样子分成面积相等的两个梯形，种上不同的蔬菜，已知这两个梯形的上底都是a米，下底都是b 米，高是(b－a)米.请你给小明家算一算，小明家的菜地的面积是多大？当a=10米，b=30米时，面积是多少？【拓展延伸】9.(10分)两个连续偶数的平方差能被4整除吗？为什么？培优训练(九)(30分钟50分)一、选择题(每小题4分，共12分)1.化简：(a+1)2－(a－1)2=( )(A)2 (B)4 (C)4a(D)2a2+22.一个正方形的边长增加了3 cm，它的面积增加了51 cm2，这个正方形原来的边长是( )(A)5 cm(B)6 cm(C)7 cm(D)8 cm3.计算5a(2－5a)－(5a+1)(－5a+1)的结果是( )(A)1－10a+50a2 (B) 1－10a(C)10a－50a2－1 (D)10a－1二、填空题(每小题4分，共12分)=______.4.100⨯+9910115.为了便于直接应用平方差公式计算，应将(a+b－c)·(a－b+c)变形为［a______］［a______］.6.(2014·万宁中考)观察下列各式，探索发现规律：22－1=1=1×3；42－1=15=3×5；62－1=35=5×7；82－1=63=7×9；102－1=99=9×11；……用含正整数n的等式表示你所发现的规律为______.三、解答题(共26分)7.(8分)利用平方差公式计算：(1)31×29. (2)×.8.(8分)计算：(1)4x 2－(2x +3)(－2x －3). (2)(3ab +12)(3ab －12)－a 2b 2.【拓展延伸】9.(10分)阅读下列材料：某同学在计算3×(4+1)(42+1)时，把3写成4－1后，发现可以连续运用平方差公式计算：3×(4+1)(42+1)=(4－1)(4+1)(42+1)=(42－1)(42+1)=162－1.很受启发，后来在求(2+1)·(22+1)(24+1)(28+1)…(21 024+1)的值时，又改造此法，将乘积式前面乘以1，且把1写为2－1得(2+1)(22+1)(24+1)(28+1)…(21 024+1) =(2－1)(2+1)(22+1)(24+1)(28+1)…(21024+1)=(22－1)(22+1)(24+1)(28+1)…(21 024+1) =(24－1)(24+1)(28+1)…(21 024+1)=…=(21 024－1)(21 024+1)=22 048－1. 回答下列问题：(1)请借鉴该同学的经验，计算： (3+1)(32+1)(34+1)(38+1).(2)借用上面的方法，再逆用平方差公式计算： (2112 )(1－213)(1－214)…(1－2110).培优训练(十)(30分钟50分)一、选择题(每小题4分，共12分)1.(2014·临沂中考)下列计算正确的是( )(A)2a2+4a2=6a4 (B)(a+1)2=a2+1 (C)(a2)3=a5 (D)x7÷x5=x22.图①是一个边长为(m+n)的正方形，小颖将图①中的阴影部分拼成图②的形状，由图①和图②能验证的式子是( )(A)(m+n)2－(m－n)2=4mn(B)(m+n)2－(m2+n2)=2mn(C)(m－n)2+2mn=m2+n2(D)(m+n)(m－n)=m2－n23.若a,b是正数，a－b=1,ab=2,则a+b=( )(A)－3 (B)3 (C)±3 (D)9二、填空题(每小题4分，共12分)4.(2014·河北中考)已知y=x－1，则(x－y)2+(y－x)+1的值为_____.5.(2014·江西中考)已知(m－n)2=8,(m+n)2=2,则m2+n2=______.6.(2014.六盘水中考)如图是我国古代数学家杨辉最早发现的，称为“杨辉三角”.它的发现比西方要早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的！“杨辉三角”中有许多规律，如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如，(a+b)2=a2+2ab+b2展开式中的系数1，2，1恰好对应图中第三行的数字；再如，(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1，3，3，1恰好对应图中第四行的数字.请认真观察此图，写出(a+b)4的展开式，(a+b)4=______.三、解答题(共26分)7.(8分)利用完全平方公式计算：(1)482.(2)1032.8.(8分)( 2014·丽水中考)已知A＝2x＋y，B＝2x－y，计算A2－B2.【拓展延伸】9.(10分)如图所示,有四个同样大小的直角三角形,两条直角边分别为a,b,斜边为c,拼成一个正方形,但中间却留有一个小正方形,你能利用它们之间的面积关系,得到关于a,b,c 的等式吗?培优训练(十一)(30分钟50分)一、选择题(每小题4分，共12分)1.下列计算36a8b6÷13a2b÷4a3b2的方法正确的是( )(A)(36÷13÷4)a8－2－3b6－1－2(B)36a8b6÷(13a2b÷4a3b2)(C)(36－13－4)a8－2－3b6－1－2(D)(36÷13÷4)a8－2－3b6－0－22.一颗人造地球卫星的速度为×107米/时，一架喷气式飞机的速度为×106米/时，则这颗人造地球卫星的速度是这架喷气式飞机的速度的( )(A)1 600倍(B)160倍(C)16倍(D)倍3.已知a3b6÷a2b2=3，则a2b8的值等于( )(A)6 (B)9 (C)12 (D)81二、填空题(每小题4分，共12分)4.计算a5b÷a3=_____.5.已知28a3b m÷28a n b2=b2，那么m=_____，n=_____.6.若(2a)3·(－b2)2÷12a3b2·M=－b8，则M=_____.三、解答题(共26分)7.(8分)计算：(1)(－3xy2)2·2xy÷3x2y5. (2)(x－y)5÷(y－x)3.8.(8分)三峡一期工程结束后的当年发电量为×109度，某市有10万户居民，若平均每户用电×103千瓦时.那么三峡工程该年所发的电能供该市居民使用多少年？【拓展延伸】9.(10分)观察下列单项式：x，－2x2，4x3，－8x4，16x5，…(1)计算一下这里任一个单项式与前面相连的单项式的商是多少？据此规律写出第n个单项式.(2)根据你发现的规律写出第10个单项式.培优训练(十二)(30分钟50分)一、选择题(每小题4分，共12分)1.对于任意正整数n，按照n→平方→+n→÷n→－n→答案程序计算，应输出的答案是( )(A)n2－n+1 (B)n2－n (C)3－n(D)12.计算［2(3x2)2－48x3+6x］÷(－6x)等于( )(A)3x3－8x2 (B)－3x3+8x2(C)－3x3+8x2－1 (D)－3x3－8x2－13.下列计算正确的是( )(A)(9x4y3－12x3y4)÷3x3y2=3xy－4xy2(B)(28a3－14a2+7a)÷7a=4a2－2a+7a (C)(－4a3+12a2b－7a3b2)÷(－4a2)=a－3b+74ab2(D)(25x2+15x2y－20x4)÷(－5x2)=－5－3xy+4x2二、填空题(每小题4分，共12分)4.填上适当的式子，使以下等式成立：2xy2+x2y－xy=xy·_____.5.如果用“★”表示一种新的运算符号，而且规定有如下的运算法则：m★n=m2n+n，则(2x★y)÷y的运算结果是_____.6.已知梯形的面积是3a3b4－ab2，上、下底的长度之和为2b2，那么梯形的高为_____.三、解答题(共26分)7.(8分)计算：(1)(64x5y6－48x4y4－8x2y2)÷(－8x2y2). (2)－12a3b2－16a4b3)÷(－.8.(8分)先化简，再求值：(a2b－2ab2－b3)÷b－(a+b)(a－b)，其中a=12，b=－1.【拓展延伸】9.(10分)一堂习题课上，数学老师在黑板上出了这样一道题：当a=2 012，b=2时，求［3a2b(b－a)+a(3a2b－ab2)］÷a2b的值.一会儿，雯雯说：“老师，您给的‘a=2 012’这个条件是多余的.”一旁的小明反驳道：“题目中有两个字母，不给这个条件，肯定求不出结果！”他们谁说得有道理？请说明理由.单元评价检测(一)第一章(45分钟100分)一、选择题(每小题4分，共28分)1.(2014·益阳中考)下列计算正确的是( )(A)2a+3b=5ab(B)(x+2)2=x2+4 (C)(ab3)2=ab6 (D)(－1)0=12.计算：2－2=( )(A)14(B)2 (C)－14(D)43.(2014·天门中考)下列运算不正确的是( )(A)a5+a5=2a5 (B)(－2a2)3=－2a6 (C)2a2·a－1=2a(D)(2a3－a2)÷a2=2a－14.若关于x的积(x－m)(x+6)中常数项为12,则m的值为( )(A)2 (B)－2 (C)6 (D)－65.(－112)2 013×(23)2 013等于( )(A)1 (B)－1 (C)－94(D)－496.若x2+mx－15=(x+3)(x+n)，则m的值为( )(A)－5 (B)5 (C)－2 (D)27. 现规定一种运算：a*b=ab+a－b，其中a,b为实数，则a*b+(b－a)*b等于( )(A)a2－b(B)b2－b(C)b2 (D)b2－a二、填空题(每小题5分，共25分)8.(2014·贺州中考)微电子技术的不断进步，使半导体材料的精细加工尺寸大幅度缩小.某种电子元件的面积大约为000 53平方毫米，用科学记数法表示为____平方毫米.9.已知(9n)2=38，则n=_____.10.要使(ax2－3x)(x2－2x－1)的展开式中不含x3项，则a=_____.11.已知(x－ay)(x+ay)=x2－16y2，那么a=_____.12.(2014·黔东南中考)如图，第(1)个图有2个相同的小正方形，第(2)个图有6个相同的小正方形，第(3)个图有12个相同的小正方形，第(4)个图有20个相同的小正方形，……，按此规律，那么第(n)个图有_____个相同的小正方形.三、解答题(共47分)13.(10分)计算：(1)(－2x+5)(－5－2x)－(x－1)2. (2)［－6a3x4－(3a2x3)2］÷(－3ax2).14.(12分)先化简，再求值：3(2a－b)2－3a(4a－3b)+(2a+b)(2a－b)－b(a+b)，其中a=1，b=2.15.(12分)在一次联欢会上，节目主持人让大家做一个猜数的游戏，游戏的规则是：主持人让观众每人在心里想好一个除0以外的数，然后按以下顺序计算：(1)把这个数加上2后平方.(2)然后再减去4.(3)再除以原来所想的那个数，得到一个商.最后把你所得到的商是多少告诉主持人，主持人便立即知道你原来所想的数是多少，你能解释其中的奥妙吗？16.(13分)新知识一般有两类：第一类是不依赖于其他知识的新知识，如“数”“字母表示数”这样的初始性的知识；第二类是在某些旧知识的基础上进行联系、推广等方式产生的知识，大多数知识是这样的知识.(1)多项式乘以多项式的法则，是第几类知识？(2)在多项式乘以多项式之前，你已拥有的有关知识是哪些？(写出三条即可)(3)请你用已拥有的有关知识，通过数和形两个方面说明多项式乘以多项式的法则是如何获得的?(用(a+b)(c+d)来说明)答案解析一1.【解析】选A.(－x) 2·x3=x2·x3=x2+3=x5.2.【解析】选D .(－c )n －1·(－c )n +1=(－c )n －1+n +1=(－c )2n =c 2n .3.【解析】选C .设S =1+5+52+53+…+52 012，则5S =5+52+53+54+…+52 013，因此，5S －S =52 013－1，S =2 013514. 4.【解析】因为4m +1=4m ×41，所以4m ×4=28，所以4m =7.答案：75.【解析】100亿千克=1010千克，所以100亿千克镭完全衰变后所放出的热量相当于375 000×1010=×105×1010=×1015(千克)煤燃烧所放出的热量.答案：×10156.【解析】因为2x ·2x ·8=2x ·2x ·23=2x +x +3，所以x +x +3=12,解得x =92. 答案：927.【解析】(1)(－3)3·(－3)4·(－3)=(－3)3+4+1=(－3)8=38.(2)a 3·a 2－a ·(－a )2·a 2=a 3+2－a ·a 2·a 2=a 5－a 5=0.(3)(2m －n )4·(n －2m )3·(2m －n )6=(n －2m )4·(n －2m )3·(n －2m ) 6=(n －2m )4+3+6=(n －2m )13.8.【解析】(1)a x +2=a x ×a 2=5a 2.(2)a x +y +1=a x ·a y ·a =5×4×a =20a .9.【解析】(1)(－2)n +(－2)n ·(－2)=(－2+1)(－2)n=－(－2)n .当n 为偶数时，原式=－2n ，当n为奇数时，原式=2n.(2)(－x)2n－1·(－x)n+2=(－x)2n－1+n+2=(－x)3n+1.当n为偶数时，原式=－x3n+1,当n为奇数时，原式=x3n+1.答案解析二1.【解析】选C.(ab)2=a2b2.2.【解析】选－a2=2a2，(－a2b)3=－a6b3，a3·a6=a9，(2a2)2=4a4，故A，B，D错误.3.【解析】选B.正方体的体积为：(2×102)3=8×106(立方毫米).4.【解析】因为22×83=22×(23)3=22×29=211，所以n=11.答案：115.【解析】因为4x×2y=(22)x×2y=22x×2y=22x+y，所以4x×2y=23=8.答案：86.【解析】(1)［(56)6×(－65)6］7=［(56)6×(65)6］7=［(5665)6］7=1.(2)82 013×(－2 012=8×82 012× 012=8×(8×2 012=8×1=8. 答案：(1)1 (2)87.【解析】(x－y)3·(2x－2y)3·(3x－3y)3=(x－y)3［2(x－y)］3［3(x－y)］3=(x－y)3·8(x－y)3·27(x－y)3=216(x－y)9=216a9.8.【解析】因为3555=3111×5=(35)111=243111，4444=4111×4=(44)111=256111，5333=5111×3=(53)111=125111，又因为125<243<256，所以125111<243111<256111，所以5333<3555<4444.9.【解析】(1)因为23=8，所以log 28=3；(2)因为24=16,所以log 216=4;(3)log 2(8×16)=log 28+log 216=3+4=7.所以依次应填：(1)23=83(2)24=164 (3)log 28 log 216 7 答案解析三1.【解析】选+a 3=2a 3,a 6÷a －3=a 9,a 3·a 3=a 6,(－2a 2)3=－8a 2×3=－8a 6.2.【解析】选D .因为3－2=21139=，所以和3－2的结果相同的数是9的倒数. 3.【解析】选－2y =3x ÷32y =3x ÷(32)y =3x ÷9y =4÷7=47. 4.【解析】本题属于开放题，答案不惟一，如a 8÷a 2=a 6(a ≠0)或a 4·a 2=a 6.答案：a 8÷a 2(a ≠0)(答案不惟一)5.【解析】因为9级地震所释放的相对能量为109，7级地震所释放的相对能量为107，所以109÷107=102=100.即9级地震所释放的相对能量是7级地震所释放的相对能量的100倍.答案：1006.【解析】a －1·a －2÷a －3=a －3÷a －3=1.答案：17.【解析】 (1)4－3×2 0130=3111464⨯=.(2)×10－3=×3110=× = 29. 8.【解析】当x －2=1时，即x =3，(3－2)3+3=16=1,满足题意；当x －2=－1时，即x =1时，(1－2)1+3=(－1)4=1，满足题意；当x =－3时，而x －2=－5≠0满足题意，所以当(x －2)x +3=1时，x 的值为3或1或－3.9.【解析】(1)①∵1－2=1，2－1=12，1＞12，∴1－2＞2－1；②∵2－3=18，3－2=19，18＞19，∴2－3＞3－2；③∵3－4=181，4－3=164，181＜164，∴3－4＜4－3；④4－5=11 024，5－4=1625，∵11 024＜1625， ∴4－5＜5－4.故答案依次为：＞＞ ＜ ＜.(2)≤2 ＞2.答案解析四1.【解析】选×10－4= 5.2.【解析】选 000 7米=7×10－7米.3.【解析】选B .因为×10－8= 000 040 3，所以原数是 004 03=×10－6.4.【解析】×10－2=.答案：5.【解析】158×10－9= 000 158米=×10－7米.答案：×10－7米6.【解析】 cm ÷100= cm = 05 m =5×10－5m .答案：5×10－57.【解析】因为百万分之一秒=6110秒=10－6秒， 又因为十亿分之一秒=9110秒=10－9秒， 所以10－6÷10－9=10－6－(－9)=103=1 000(次).所以百万分之一秒可以完成1 000次存储.8.【解析】×10－7米=×10－7×106=微米.×10－7米= 000 78米，09÷(2× 000 78)≈58(个).9.【解析】由1微米=10－6米，可求出一根头发直径为10－6×60=6×10－5(米).由圆的面积公式S =πr 2可得一根头发的横断面的面积为×(56102-⨯)2=×10－9(平方米).10万根头发捆绑起来的横断面面积为：×10－9×105=×10－4(平方米).答案解析五1.【解析】选C .(2a )3·a 2=8a 5.2.【解析】选A .|－3|=3；－(－12)=12；(a 3)2=a 6；2a ·3a =6a 2，故选A .3.【解析】选B .因为－2m 2·4n 3=－8m 2n 3,所以□内应填4n 3.4.【解析】(－2x )3·(－5xy 2)=(－8x 3)·(－5xy 2)=40x 4y 2.答案：40x 4y 25.【解析】因为x m +1y n －2·x m y 2=x 2m +1y n ，所以2m +1=5，n =3，所以m n =23=8.答案：86.【解析】当a 与2a 重合时，其乘积为2a 2；当b 与－2b 重合时，其乘积为－2b 2. 答案：2a 2(或－2b 2)7.【解析】因为1+2+3+…+n =m ，所以(ab n )·(a 2b n －1)…(a n －1b 2)·(a n b )=a 1+2+…+n b n +n －1+…+1=a m b m .8.【解析】拼法不惟一，现列举5种：(1)长为18a，宽为a，高为a，体积为18a·a·a=18a3；(2)长为9a，宽为2a，高为a，体积为9a·2a·a=18a3；(3)长为6a，宽为3a，高为a，体积为6a·3a·a=18a3；(4)长和宽都为3a，高为2a，体积为3a·3a·2a=18a3；(5)长为3a，宽为2a，高为3a，体积为3a·2a·3a=18a3.可以发现，不管怎样拼，体积总是18a3.9.【解析】×=2mn3·(－3n5m)2=2mn3·9n10m2=18n13m3.答案解析六1.【解析】选A.－3xy·(4y－2x－1)=－3xy·4y+(－3xy)·(－2x)+(－3xy)·(－1)=－12xy2+6x2y+3xy，所以应填写3xy.2.【解析】选D.(x2+ax+1)(－6x3)=－6x5－6ax4－6x3.展开式中不含x4项，则－6a=0，所以a=0.3.【解析】选A.因为a2(－a+b－c)=－a3+a2b－a2c；－a(a2－ab+ac)=－a3+a2b－a2c，所以两式相等.4.【解析】－2a(b2+ab)+(a2+b)b=－2ab2－2a2b+a2b+b2=－2ab2－a2b+b2.答案：－2ab2－a2b+b25.【解析】2x(x－1)－x(2x+3)=15，去括号，得2x2－2x－2x2－3x=15，－5x=15，所以x=－3.答案：－36.【解析】因为长方形的长是2a，宽是a+b，所以上图的面积是2a(a+b).因为长方形的面积为a2+a2+ab+ab=2a2+2ab，所以2a(a+b)=2a2+2ab.答案：2a(a+b)=2a2+2ab7.【解析】这个多项式是(x2－4x+1) －(－3x2)=4x2－4x+1，正确的计算结果是：(4x2－4x+1)·(－3x2)=－12x4+12x3－3x2.8.【解析】由题意可得：这个长方形的宽为(a+b)－(a－b)=2b(cm)，长方形的周长为2(a+b+2b)=2a+6b(cm)，长方形的面积为(a+b)×2b=2ab+2b2(cm2).9.【解析】(1)防洪堤坝的横断面积S=12［a+(a+2b)］×12a=14a(2a+2b)=1 2a2+12ab.故防洪堤坝的横断面面积为(12a2+12ab)平方米.(2)堤坝的体积V=(12a2+12ab)×100=50a2+50ab.故这段防洪堤坝的体积是(50a2+50ab)立方米.答案解析七1.【解析】选C.因为(2a－3)(3a－1)=6a2－11a+3；(m+n)(n+m)=m2+2mn+n2；(a－2)(a+3)=a2+a－6；(1－a)(1+a)=1－a2，故正确的有2个.2.【解析】选B.(x+a)(x+b)=x2+(a+b)x+ab，又因为(x+a)(x+b)=x2－13x+36，所以a+b=－13.3.【解析】选B.由题意知这条边上的高为2m+2，所以这个三角形的面积为12(m+2)(2m+2)=1(2m2+6m+4)=m2+3m+2.24.【解析】(a－3)(a+2)=a2－a－6，因为a2－a+5=0，所以a2－a=－5，所以原式=－5－6=－11.答案：－115.【解析】由题意可得(x+1)(y－1)=xy－x+y－1.答案：xy－x+y－16.【解析】长为3a+b、宽为a+2b的大长方形的面积为(3a+b)(a+2b)=3a2+2b2+7ab；A类卡片的面积为a·a=a2；B类卡片的面积为b·b=b2；C类卡片的面积为a·b=ab.因此，拼成一个长为3a+b，宽为a+2b的大长方形，需要3张A类卡片、2张B类卡片和7张C 类卡片.答案：77.【解析】因为n(n+7)－(n+3)(n－2)=n2+7n－(n2+n－6)=6n+6=6(n+1)，所以当n为正整数时，6(n+1)总能被6整除.8.【解析】(1)观察图乙得知，长方形的长为a+2b，宽为a+b，所以面积为(a+2b)(a+b).又因为这个图形由6部分组成，所以其面积为a2+ab+ab+ab+b2+b2 =a2+2b2+3ab，所以(a+b)(a+2b)=a2+2b2+3ab，(2)如图所示：恒等式是(a+b)(a+b)=a2+2ab+b2.(答案不惟一)9.【解析】(1)①因为5+2=7，所以左边的三位数是275，右边的三位数是572，所以52×275=572×25.②因为左边的三位数是396，所以左边的两位数是63，右边的两位数是36，63×396=693×36.(2)因为左边两位数的十位数字为a，个位数字为b，所以左边的两位数是10a+b，三位数是100b+10(a+b)+a，右边的两位数是10b+a，三位数是100a+10(a+b)+b，所以一般规律的式子为：(10a+b)×［100b+10(a+b)+a］=［100a+10(a+b)+b］×(10b+a)，理由：左边=(10a+b)×［100b+10(a+b)+a］=(10a+b)(100b+10a+10b+a)=(10a+b)(110b+11a)=11(10a+b)(10b+a)，右边=［100a+10(a+b)+b］×(10b+a)=(100a+10a+10b+b)(10b+a)=(110a+11b)(10b+a)=11(10a+b)(10b+a)，左边=右边，所以“数字对称等式”一般规律的式子为：(10a+b)×［100b+10(a+b)+a］=［100a+10(a+b)+b］×(10b+a).答案解析八1.【解析】选C.－b是相同的项，互为相反数的项是3a与－3a，故结果是(－b)2－(3a)2=b2－9a2.2.【解析】选C.因为C中正确的算式应是(a+1)(a2－a+1)=a3+1.3.【解析】选D.因为(x+9)(x－9)=x2－81；(x+9)(－x－9)=－x2－18x－81；(－x+9)(－x－9)=x2－81；(－x－9)(x－9)=81－x2，所以选D.4.【解析】(x+y)(x－y)+y2=x2－y2+y2=x2=32=9.答案：95.【解析】因为(a+b+1)(a+b－1)=63，即(a+b)2－1=63，所以(a+b)2=64，所以a+b=±8. 答案：±86.【解析】(x－1)(x n+x n－1+…+x+1)=x n+1－1.答案：x n+1－17.【解析】以b为边长的正方形面积大.因为a，b，c是三个连续的正整数(a＜b＜c)，所以a=b－1，c=b+1，所以以c，a为长和宽所作长方形的面积为ac=(b－1)·(b+1)=b2－1.又因为以b为边的正方形的面积为b2，且b2－1＜b2，所以以b为边长的正方形面积大.8.【解析】由题意得，菜地的面积为：(a+b)(b－a)=(b2－a2)(平方米).2×12当a=10米，b=30米时，b2－a2=302－102=900－100=800(平方米).答：小明家的菜地面积为(b2－a2)平方米，当a=10米，b=30米时，其面积为800平方米.9.【解析】设两个连续偶数为2n ，2n +2，则有 (2n +2)2－(2n )2 =(2n +2+2n )(2n +2－2n ) =(4n +2)×2 =4(2n +1). 因为n 为整数，所以4(2n +1)中的2n +1也是整数， 所以4(2n +1)是4的倍数.答案解析九1.【解析】选C .(a +1)2－(a －1)2=［(a +1)－(a －1)］·［(a +1)+(a －1)］=2×2a =4a .2.【解析】选C .设原来的边长为x cm ， 则(x +3)2－x 2=51,所以(x +3+x )(x +3－x )=51，(2x +3)×3=51， 所以2x +3=17，解得x =7.3.【解析】选D .原式=10a －25a 2－(1－25a 2) =10a －25a 2－1+25a 2=10a －1.4.【解析】100991011⨯+=()()22100100100110011001110011100100===-++-+.答案：11005.【解析】通过观察发现两个多项式中a 完全相同，而b ，c 前的符号相反，所以把b －c 看作一项，构造平方差公式为［a +(b －c )］［a －(b －c )］=a 2－(b －c )2. 答案：+(b －c )－(b －c )6.【解析】观察式子，每个式子中等号左边的被减数是偶数的平方，减数都是1，等号右边是此偶数前后两个连续奇数的乘积，所以用含正整数n 的等式表示其规律为(2n )2－1=(2n －1)(2n +1).答案：(2n ) 2－1=(2n －1)(2n +1)7.【解析】(1)31×29=(30+1)(30－1)=302－12=900－1=899. (2)×=(10－(10+=102－=100－=. 8.【解析】(1)4x 2－(2x +3)(－2x －3) =4x 2+4x 2+12x +9 =8x 2+12x +9.(2)(3ab +12)(3ab －12)－a 2b 2 =(3ab )2－(12)2－a 2b 2=9a 2b 2－14－a 2b 2=8a 2b 2－14.9.【解析】(1)(3+1)(32+1)(34+1)(38+1)=12(32－1)(32+1)(34+1)(38+1)=12(34－1)(34+1)(38+1)=12(38－1)(38+1) =12(316－1). (2) (2112-)(1－213)(1－214)…(1－2110)=(1－12)(1+12)(1－13)(1+13)…(1－110)(1+110)=132491122331010⨯⨯⨯⨯⨯⨯L =111210⨯=1120. 答案解析十1.【解析】选D .选项A 结果为6a 2，选项B 结果为a 2+2a +1，选项C 结果为a 6.2.【解析】选B .根据图示可知，阴影部分的面积是边长为m +n 的正方形减去中间白色的正方形的面积m 2+n 2，即(m +n )2－(m 2+n 2)=2mn .3.【解析】选B .因为a －b =1,ab =2,可将a －b =1两边同时平方,ab =2两边同乘以4,两式相加可得(a+b)2=9.又a，b为正数，从而B正确.4.【解析】由y=x－1得y－x=－1，所以(x－y)2+(y－x)+1=(y－x)2+(y－x)+1=(－1)2+(－1)+1=1.答案：15.【解析】两式相加得：m2－2mn+n2+m2+2mn+n2=10，所以2(m2+n2)=10,所以m2+n2=5.答案：56.【解析】(a+b)4=a4+4a3b+6a2b2+4ab3+b4答案：a4+4a3b+6a2b2+4ab3+b47.【解析】(1)482=(50－2)2=2 500－200+4=2 304.(2)1032=(100+3)2=10 000+600+9=10 609.8.【解析】A2－B2＝(2x＋y)2－(2x－y)2＝(4x2＋4xy＋y2)－(4x2－4xy＋y2)＝4x2＋4xy＋y2－4x2＋4xy－y2＝8xy.9.【解析】因为小正方形的边长为b－a，所以它的面积为(b－a)2,所以大正方形的面积为4×1×a×b+(b－a)2.2又因为大正方形的面积为c2,所以4×12×a×b+(b－a)2=c2,即2ab+b2－2ab+a2=c2,得a2+b2=c2.答案解析111.【解析】选÷13a2b÷4a3b2=(36÷13÷4)a8－2－3b6－1－2.2.【解析】选C.×107)÷×106)=(2. 88÷×(107÷106)=×10=16，所以这颗人造地球卫星的速度是这架喷气式飞机的速度的16倍.3.【解析】选B.因为a3b6÷a2b2=3，即ab4=3，所以a2b8=ab4·ab4=3×3=9.4.【解析】a5b÷a3=(a5÷a3)·b=a2b.答案：a2b5.【解析】因为28a3b m÷28a n b2=a3－n b m－2，所以3－n=0，m－2=2，解得m=4，n=3. 答案：4 36.【解析】因为(2a)3·(－b2)2÷12a3b2=8a3b4÷12a3b2=23b2，所以23b2·M=－b8，M=－b8÷23b2=－32b6.答案：－32b67.【解析】(1)(－3xy2)2·2xy÷3x2y5=9x2y4·2xy÷3x2y5=18x3y5÷3x2y5=6x.(2)(x－y)5÷(y－x)3=(x－y)5÷［－(x－y)3］=－(x－y)5－3=－(x－y)2=－x2+2xy－y2.8.【解析】该市用电量为×103×105=×108，×109)÷×108)=÷×109－8=20(年).答：三峡工程该年所发的电能供该市居民使用20年.9.【解析】(1)－2x,(－2)n－1·x n.(2)第n个单项式为(－2)n－1·x n，则第10个单项式为－512x10.答案解析121.【解析】选D.由题意，有(n2+n)÷n－n=n+1－n=1.2.【解析】选C.［2(3x2)2－48x3+6x］÷(－6x)=(18x4－48x3+6x)÷(－6x)=－3x3+8x2－1.3.【解析】选C.因为(9x4y3－12x3y4)÷3x3y2=3xy－4y2；(28a3－14a2+7a)÷7a=4a2－2a+1；(－4a3+12a2b－7a3b2)÷(－4a2)=a－3b+74ab2；(25x2+15x2y－20x4)÷(－5x2)=－5－3y+4x2，所以A，B，D错误，C正确.4.【解析】因为(2xy2+x2y－xy)÷xy=2y+x－1，所以2xy2+x2y－xy=xy·(2y+x－1).答案：(2y+x－1)5.【解析】(2x★y)÷y=［(2x)2y+y］÷y=(4x2y+y)÷y=4x2+1.答案：4x2+16.【解析】梯形的高为2(3a3b4－ab2)÷2b2=(6a3b4－2ab2)÷2b2=3a3b2－a.答案：3a3b2－a7.【解析】(1)(64x5y6－48x4y4－8x2y2)÷(－8x2y2)=64x5y6÷ (－8x2y2)－48x4y4÷(－8x2y2)－8x2y2÷(－8x2y2)=－8x3y4+6x2y2+1.(2) －12a3b2－16a4b3)÷(－=－÷+12a3b2÷+16a4b3÷=－+ab +13a 2b 2.8.【解析】(a 2b －2ab 2－b 3)÷b －(a +b )(a －b ) =a 2b ÷b －2ab 2÷b －b 3÷b －(a 2－b 2) =a 2－2ab －b 2－a 2+b 2 =－2ab ，当a =12,b =－1时，原式=－2×12×(－1)=1. 9.【解析】因为［3a 2b (b －a )+a (3a 2b －ab 2)］÷a 2b =(3a 2b 2－3a 3b +3a 3b －a 2b 2)÷a 2b =2a 2b 2÷a 2b =2b ，所以化简的结果中不含a ，这样代入求值就与a 无关，所以雯雯说得有道理.答案解析 单元检测1.【解析】选D .选项A 不是同类项，不能合并;选项B 中乘法公式应用错误;选项C 应为a 2b 6,错误；选项D 正确.2.【解析】选－2=21124. 3.【解析】选B .(－2a 2)3=－8a 6.4.【解析】选B .(x －m )(x +6)=x 2+6x －mx －6m =x 2+(6－m )x －6m ，得－6m =12，m =－2.5.【解析】选B .原式=(－32)2 013×(23)2 013=(－32×23)2 013=－1. 6.【解析】选C .因为(x +3)(x +n )=x 2+(3+n )x +3n ， 所以3n =－15,n =－5；3+n =m ，即m =3－5=－2. 7.【解析】选*b +(b －a )*b =ab +a －b +(b －a )b +(b －a )－b =ab +a －b +b 2－ab +b －a －b=b2－b.8.【解析】000 53=×10－7答案：×10－79.【解析】因为(9n)2=92n=(32)2n=34n，所以4n=8，n=2.答案：210.【解析】原式=ax4－2ax3－ax2－3x3+6x2+3x=ax4－(2a+3)x3－(a－6)x2+3x，因为展开式中不含x3项，所以2a+3=0，a=－3.2答案：－3211.【解析】因为(x－ay)(x+ay)=x2－a2y2，所以a2=16，a=±4.答案：±412.【解析】第(1)个图有2个相同的小正方形，而2=1×2；第(2)个图有6个相同的小正方形，而6=2×3；第(3)个图有12个相同的小正方形，而12=3×4；第(4)个图有20个相同的小正方形，而20=4×5；……所以第(n)个图有n(n+1)个相同的小正方形.答案：n(n+1)13.【解析】(1)(－2x+5)(－5－2x)－(x－1)2=(－2x+5)(－2x－5)－(x－1)2=4x2－25－(x2－2x+1)=4x2－25－x2+2x－1=3x2+2x－26.(2)［－6a3x4－(3a2x3)2］÷(－3ax2)=(－6a3x4－9a4x6)÷(－3ax2)=－6a3x4÷(－3ax2)－9a4x6÷(－3ax2)=2a2x2+3a3x4.14.【解析】3(2a－b)2－3a(4a－3b)+(2a+b)(2a－b)－b(a+b)=3(4a2－4ab+b2)－(12a2－9ab)+(4a2－b2)－(ab+b2)=12a2－12ab+3b2－12a2+9ab+4a2－b2－ab－b2=4a2－4ab+b2，当a=1，b=2时，原式=4×12－4×1×2+22=0.15.【解析】设这个数为x，据题意得，［(x+2)2－4］÷x=(x2+4x+4－4)÷4=x+4.如果把这个商告诉主持人，主持人只需减去4就知道这个数是多少.16.【解析】(1)是第二类知识.(2)单项式乘以多项式(分配律)、字母表示数、数可以表示线段的长或图形的面积等.(3)用数来说明：(a+b)(c+d)=(a+b)c+(a+b)d=ac+bc+ad+bd.用形来说明：如图，边长分别为a+b和c+d的矩形，分割前后的面积相等，即(a+b)(c+d)=ac+bc+ad+bd.。

初中数学《整式的乘除》培优、拔高（奥数）专题讲义阅读与思考指数运算律是整式乘除的基础，有以下5个公式：a m a n=a m4n, （a m）n = a mn, （ab）n = a n b n,a m+a n =a m"（a #0）, a0=1（a¥0）, a"=1（a¥0）.a p学习指数运算律应注意：1.运算律成立的条件；2.运算律中字母的意义：既可以表示一个数，也可以表示一个单项式或者多项式；3.运算律的正向运用、逆向运用、综合运用.多项式除以多项式是整式除法的延拓与发展，方法与多位数除以多位数的演算方法相似，基本步骤是:1.将被除式和除式按照某字母的降哥排列，如有缺项，要留空位；2.确定商式，竖式演算式，同类项上下对齐；3.演算到余式为零或余式的次数小于除式的次数为止.例题与求解【例1】（1）若n为不等式n200> 6300的解，则n的最小正整数的值为 .（华罗庚杯”香港中学竞赛试题）（2）已知x2 +x =1 ,那么x4 +2x3 —x2 -2x + 2005 =. （华杯赛”试题）（3）把（x2—x+1）6 展开后得ai2x12+&1/+|||+a2x2+a1x + a0 ,则a12 +a10 +a8 +a6 +a4 +a2 +a0 = （祖冲之杯”邀请赛试题）（4）若x5 -3x4 +7x3 -6x2 +2x + 9 = （x - a）（x - b）（x -c）（x -d ）（x -e）则ab+ac + ad +ae + bc + bd+be + cd +ce+de=. （创新杯训练试题）解题思路：对于（1）,从哥的乘方逆用入手；对于（2）,目前无法求x值，可考虑高次多项式用低次多项式表示；对于（3）,它是一个恒等式，即在x允许取值范围内取任何一个值代入计算，故可考虑赋值法；对于（4）,可考虑比较系数法.1 1【例2】已知25x =2000 , 80y =2000，则一十一等于（）x y，一一 1 1 x yx, y 的值，而一十—= ,所以只需求出 x+y,xy 的值或x y xy它们的关系，于是自然想到指数运算律.【例3】设a,b,c,d 都是正整数，并且a5=b 4,c 3 =d 2,c —a =19 ,求d —b 的值.（江苏省竞赛试题）解题思路：设a5=b 4 =m 20,c 3 =d 2=n 6,这样a,b 可用m 的式子表示，c,d 可用n 的式子表示，通过减少字母个数降低问题的难度.m 3 1 ,,【例 4】已知多项式 2x +3xy —2y —x+8y-6 = (x + 2y + m)(2 x - y + n),求 ——的值. n - 1解题思路：等号左右两边的式子是恒等的，它们的对应系数对应相等，从而可考虑用比较系数法.【例5】是否存在常数p,q 使得x4+ px 2 +q 能被x 2+2x+5整除？如果存在，求出 p,q 的值，否则请说 明理由.解题思路：由条件可推知商式是一个二次三项式（含待定系数），根据被除式=除式 X 式”，运用待定系数法求出p,q 的值，所谓p,q 是否存在，其实就是关于待定系数的方程组是否有解.【例6】已知多项式2x 4 -3x3+ax 2 +7x + b 能被x 2 +x-2整除，求-的值.（北京市竞赛试题）bA. 2B. 1 D.（“希望杯”邀请赛试题）解题思路：x,y 为指数，我们无法求出解题思路：本题主要考查了待定系数法在因式分解中的应用. 本题关键是能够通过分析得出当x = -2和x=1时，原多项式的值均为0,从而求出a,b的值.当然本题也有其他解法.能力训练A级.24 23 . ...........1. （1） 4 M（—0.25）—1=. （福州市中考试题）（2）若a2n =3 ,则2a6n -1 =. （广东省竞赛试题）2.若2x +5y -3=0 ,则4x U2y.3.满足（x -1 ）200> 3300的x的最小正整数为 . （武汉市选拔赛试题）4. a,b,c,d 都是正数，且a2 =2,b3 =3,c4 =4,d5 =5 ,则a,b,c,d 中，最大的一个是 .（“英才杯”竞赛试题）5.探索规律：31 =3,个位数是3; 32=9,个位数是9; 33 =27,个位数是7；34=81,个位数是1;35 =243,个位数是3; 36=729,个位数是9;…那么37的个位数字是, 330的个位数字是. （长沙市中考试题）6.已知a =8131,b =2741,c = 961,则a,b,c 的大小关系是（）A. a >b >cB. a >c >bC. a<b<cD. b >c> a 55 44 33 227.已知a =2 ,b =3 ,c = 5 ,d =6 ,那么a,b,c,d从小到大的顺序是（）A . a<b<c<d B. a<b<d<c C. b <a <c<d D. a<d<b<c（北京市“迎春杯”竞赛试题）8.若x =2n++2n, y =2n4+2T ,其中n为整数，则x与y的数量关系为（）B.y=4xC.x=12y（江苏省竞赛试题）9.已知2a =3,2b =6,2c =12，则a,b,c的关系是A.2b<a+cB.2b = a +cC.2b〉a + cD. a b c（河北省竞赛试10.化简2n 4 -2(2n) 2(2n 3)A.2nJB.~2n*C.-87 D.—2 . 23 . 3 4.411.已知ax + by =7, ax +by =49,ax +by =133,ax +by =406,、…17 .一试求1995(x + y) +6xy - - (a +b)的值.12.已知6x2 -7xy -3y2 +14x + y +a = (2x -3y +b)(3x + y +c).试确定a,b, c的值.13.已知x3+kx2+3除以x+3,其余数较被x+1除所得的余数少2,求k的值.（香港中学竞赛试题）（青少年数学周“宗沪杯”竞赛试题）3. （1） 1516与3313的大小关系是15163313 （填 4"之"建"）.. 23 2 4.如果x +x -1 =0,则x 3 +2x 2 +3=.（“希望杯”邀请赛试题）55. 43. 25 .已知（x +2） =ax +bx +cx +dx +ex+ f ,贝U 16b +4d + f =.（“五羊杯”竞赛试题）6 .已知a,b,c 均为不等于1的正数，且a" =b 3= c 6,则abc 的值为（）…1A. 3B. 2C. 1D.一2（CASIO 杯”武汉市竞赛试题）7,若 x 3 +x 2 +x+1 =0 ,则 x^7 +x* +IH+x'+1+x+x 2+||| 十 x 26 + x 27 的值是（）A. 1B. 0C. -1D. 2.一 328 .如果x +ax +bx +8有两个因式x+1和x+2 ,则a + b =（）A. 7B. 8C. 15D. 21（奥赛培训试题）9 .已知 a 1，a 2, a 3,川 a 1996, a 1997 均为正数，又 M = （a ] + a ? ’a ）996 ）L （a 2 + a 3 +…* a-?）,N =（a 1 +a 2 +…+ a [997）L （a 2 +a 3 +… 匕语），则M 与N 的大小关系是（）A. M =NB. M <NC. M >ND.关系不确定1.已知 2a=3,4b =5,8c =7,则8a*Nb =（第16届“希望杯”邀请竞赛试题）（2） 如果5555_5_5_5_5_5_54 4 4 46 6 6 6 6 6 25• 25= 2n, 32001 -1 32002 1 的大小关系是:32000 , 1 32001 1 32001 - 1 32002-2. （1）计算:c20002000315V ___________________ -,2000 CL 200010.满足（n2 -n -1）nH2 =1的整数门有（）个A. 1B. 2C. 3D. 411.设a,b,x, y 满足ax +by =3,ax2 +by2 = 7,ax3 +by3 =16,ax4 +by4 = 42,求ax5 +by5的值.512.右x, y,z, w 为整数，且x>y〉z>w, 2 +2 +2 +2 = 20—，求(x+y + z + w — 1) 的值.8(美国犹他州竞赛试题)13.已知a, b,c为有理数，且多项式x3+ax2+bx+c能够被x2+3x — 4整除.(1)求4a +c的值；(2)求2a-2b-c 的值；(3)若a,b,c为整数，且c> a >1.试比较a,b,c的大小.(四川省竞赛试题)。

整式的乘除 一、选择题 1、以下式子运算结果是m 2n 4－2mn 2+1的是( )A.(m 2n+1)2B. (m 2n-1)2C. (mn 2-1)2 D. (mn 2+1)2 2、已知a+b=10，ab=24,则a 2+b 2等于（ ）A.52B.148C.58D.763、若(x －1)(x +3)＝x 2+mx +n ，那么m ,n 的值分别是( )A.m =1，n =3B.m =4，n =5C.m =2，n =－3D.m =－2 ，n =34、设()()A b a b a +-=+223535，则A =（ ） A. 30ab B. 60ab C. 15ab D. 12ab5、已知,5,3==ba x x 则=-b a x 23（ ） A. 2527 B. 109 C. 53 D. 52 6、通过计算几何图形的面积可表示一些代数恒等式，如图可表示的代数恒等式是（ ）A ．()2222a b a ab b -=-+B ．()2222b ab a b a ++=+C ．()ab a b a a 2222+=+D ．()()22a b a b a b +-=-7、乘积)200011)(199911()311)(211(2222----等于( )． A ．20001999 B ．20002001 C ．40001999 D ．40002001 8、如果(x +p )(x +5)的乘积中不含x 的项，那么p 等于（ ）A 、5B 、－5C 、0D 、－109、若x 是不为0的有理数，已知)12)(12(22+-++=x x x x M ，)1)(1(22+-++=x x x x N ，则M 与N 的大小是（ ）A ．M>NB ． M<NC ． M=ND ．无法确定10、在1，2，3，……，98共98个自然数中，能够表示成两整数的平方差的数有（ ）个A 、8B 、10C 、12D 、15二、填空题1、已知x 2-y 2=6,x+y=3,则x-y=__________.2、若a －b ＝1，ab=-2，则(a ＋1)(b －1)＝___________________.3、已知2514x x -=，求()()()212111x x x ---++的值nmb a4、方程()()()()41812523=-+--+x x x x 的解是_______5、当2y –x =5时，()()6023252-+---y x y x =6、若4x 2＋kx ＋25＝(2x －5)2，那么k 的值是7、若1007=+y x ，2x y -=，则代数式22x y -的值是8、一个正方形的边长增加了cm 2，面积相应增加了232cm ，则这个正方形的边长为____9、如图，甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式：①(2a +b )(m +n );②2a (m +n )+b (m +n );③m (2a +b )+n (2a +b ); ④2am +2an +bm +bn ，你认为其中正确的有___________________(填序号） 10、若622=-n m ，且3=-n m ，则=+n m ． 三、解答题1、计算下列各题：（1）()()()()233232222x y x xy y x ÷-+-⋅ （2） ()()222223366m m n m n m -÷--（3）)12)(12(-+++y x y x （4）)2)((4)2(2y x y x y x +---（5）2(a+1)2－4(a+1)(a-1)+3(a-1)2 （6）1)17()17()17()17(6842++⨯+⨯+⨯+⨯(7)1.345×0.345×2.69—1.3452一1.345×0.3452．（巧算 设0.345=a ）2、已知)1()3)(3(1,09322---+++=-+x x x x x x x ）求（的值.3、先化简，再求值：（1）2b 2+(a +b )(a －b )－ (a －b )2， （2）22(2)(2)2(2)(2)a b a b a b a b ++---+ 其中a =－3,b =21. 其中26279b a ==．4、（1）已知5=+b a ，6=ab ，求 （2）已知13x x -=，求 x 2+ 1x 222b a +，2)(b a -，33b a +的值。

整式的乘法与除法数学更高的价值在于培养纯粹的思维能力，启发人们向往理念的端倪，便于将灵魂从变化的世界转向真理的存在。

——柏拉图《理想国》 知识枞横指数运算律是整式乘除的基础，有以下四个：n m n m n m n mn n m n m a a a b a ab a a a a -+=÷===•,)(,)(,b n m 。

学习指数运算律应注意：1．运算律成立的条件；2．运算律字母的意义：既可以表示一个数，也可以是一个单项式或者多项式； 3．运算律的正向运用、逆向运用、综合运用。

多项式除以多项式是整式除法的延拓与发展，方法与多位数除以多位数的演算方法相似，基本步骤是：1．将被除式和除式按照某字母的降幂排列，如有缺项，要留空位； 2．确定商式、竖式演算式，同类项上下对齐； 3．演算到余式为零或余式的次数小于除式的次数为止。

【例题1】（1）把621x ）（+-x 展开后得022********...a x a x a x a x a +++++，则024681012a a a a a a a ++++++= ；（“祖冲之杯”邀请赛）（2）已知882210322)2(...)2()2(71+++++++=-+x a x a x a a x x ）（）（，则7654321a a a a a a a +-+-+-= ；（“祖冲之杯”邀请赛） 思路点拨 我们很难将相应多项式的展开式写出，因此想通过展开式去求出每一个系数是不实际的，事实上，上列等式在的x 允许值范围内取任何一个值代入计算，等式都成立，考虑赋值法解。

[例2]已知,200025x =,200080y =则yx 11+等于（ ） A ．2 B ． 1 C ．21 D ．23 （“希望杯”邀请赛试题）思路点拨 因x 、y 为指数，我们目前无法求出x 、y 的值，xyyx y +=+1x 1，其实只需求出xy y x 、+的值或他们的关系，自然想到指数运算律。

第 12 章整式的乘除幂的运算专题一与幂的计算有关的研究题1. 我们商定 a&b=10a×10b，如 2&3=102× 103=105，那么 4&8为（）A． 3232 12D ． 1210 B．10 C ．102. 已知 10a=3， 10b=5， 10c =7，试把 105 写成底数是10 的幂的形式 ___________．3. 小丽给小明出了一道计算题：若（-3x（ -32 3 7） ? ） ? （ -3 ） =（ -3 ），求 x 的值，小明的答案是 -2 ，小亮的答案是2，你以为 ___________的答案正确（请填“小丽”、“小明”或“小亮”）．并说明原因.4．我们规定： a*b=10 a× 10b，比如 3*4=10 3×104=107．（1）试求 12*3 和 2*5 的值；（2）想想（ a*b ）*c 与 a* （ b*c ）相等吗假如相等，请考证你的结论．专题二阅读理解题2 3 4 2013的值，可令2 3 4 20135. 为了求 1+2+2 +2 +2 + +2 S=1+2+2 +2 +2 + +2 ，则 2S=2+22+23+24+ +22013+22014，所以 2S-S=（ 2+22 +23+ +22013+22014） - （ 1+2+22+23++22013） =22014-1 ．所以： S=22014-1 ．即 1+2+22+23+24++22013=22014-1 ．请依据此法，求：1+4+42+43 +44++42013的值．6.阅读以下解题过程，试比较2100与 375的大小．解：∵ 2100=（ 24）25=1625， 375=（ 33）25=2725，，而 16＜27,∴2100＜ 375.请依据上述解答过程解答：若 a=2555， b=3444，c=4333， d=5222，试比较a、 b、c、 d 的大小．（写出过程）状元笔录：[ 知识重点 ]1.同底数幂的乘法法例：同底数幂相乘，底数不变，指数相加. 即 a m· a n=a m+n(m、 n 都是正整数） .a m表示 m个 a 相乘， a n表示 n 个 a 相乘， a m·a n表示 m个 a 相乘再与 n 个 a 相乘，依据乘方的意义可得 a m· a n =a m+n.2.幂的乘方是指几个同样的幂相乘法例：幂的乘方，底数不变，指数相乘．即(a m) n=a mn（ m， n 都是正整数） .3.积的乘方是指底数是乘积形式的乘方法例：积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘，即（ ab) n=a n b n（ n 是正整数）．4.同底数幂的除法法例：同底数幂相除，底数不变，指数相减．即 a m÷ a n= a m-n（ a≠ 0， m，n 都是正整数，且m>n)．参照答案1. C 【分析】 4&8=104× 108=1012．应选 C．2. 10 a+b+c【分析】 105=3× 5× 7，而 3=10a b c，∴ 105=10ab ca+b+c，5=10 ， 7=10 ? 10? 10 =10 .故应填 10a+b+c．3.小亮【分析】小亮的答案是正确的．原因以下：∵（ -3 ）x? （ -3 ）2? （ -3 ）3 =（ -3 ）x+2+3=（ -3 ）7，∴ x+2+3=7，解得 x=2．故填小亮．4.解：（ 1） 12*3=10 12×103=1015， 2*5=10 2× 105=107；a b a b（2）相等．∵（ a*b ）*c= （ 10a× 10b）*c= 1010× 10c=1010+c，a*（b*c）=a*（10b×10c）=10a+10b+c．∴（ a*b ） *c ≠ a* （ b*c ）．5.解：为了求1+4+42+43+44+ +42013的值，可令S=1+4+42+43+44++42013，则 4S=4+42+43+44+ +42014，所以 4S-S=（ 4+42 +43+44+ +42014） - （ 1+4+42+43+44++42013）=42014-1 ，所以 3S=42014-1 ，所以 S=1（42014-1 ），3即 1+4+42+43+44+ +42013= 1（ 42014-1 ）．36.解：∵ a=2555，b=3444，c=4333，d=5222，∴a=（ 25）111， b=（34）111， c=（ 43）111， d=（ 52）111，∴a=32111， b=81111， c=64111， d=25111．∵81＞ 64＞32＞ 25，∴81111＞ 64111＞ 32111＞ 25111，∴b＞ c＞ a＞ d．整式的乘法专题阅读研究题1.阅读以下解答过程，并回答以下问题．在（x2+ax+b）与（ 2x2-3x-1 ）的积中， x3系数为 -5 ，x2系数为 -6 ，求 a， b 的值．解： (x 2+ax+b） ? （ 2x2-3x-1 ） =2x4-3x 3+2ax3+3ax2-3bx①=2x4- （ 3-2a ） x3- （ 3a-2b ） x2-3bx..②3 2a 5依据对应项系数相等，有. ③3a 2b 6回答：（1）上述解答过程能否正确 ____________．（2）若不正确，从第_________步开始出现错误，其余步骤能否还有错误__________________ ．（ 3）写出正确的解答过程．2.（ 1）计算（ x+1）（ x+2）=_____________ ，（x-1 ）（ x-2 ）=___________，（x-1 ）（ x+2）=__________，（x+1）（ x-2 ）=_______________．（2）你发现（ 1）小题有何特点，会用公式表示出来吗？（3）已知 a、 b、 m均为整数，且（ x+a）（ x+b） =x2+mx+12，则 m的可能取值有多少个状元笔录【知识重点】1.单项式与单顶式相乘法例：单项式与单项武相乘，把它们的系数、同样字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式．2.单项式与多项式相乘法例：单项式与多项式相乘，就是依据分派律用单项式去乘多项式的每一项，再把所得的积相加．3.多项式与多项式相乘法例：多项式与多项式相乘，先用一个多项式的每一项分别乘另一个多项式的每一项，再把所得的积相加.【方法技巧】1.先利用乘法交换律和乘法联合律，再利用同底数幂的乘法法例可达成单项式乘法．关于法例不要照本宣科，要注意以下几点：(1)积的系数等于各单项式的系数的积，应先确立符号后计算绝对值．(2)要注意只在一个单项式里含有的字母要连同它的指数写在积里，不可以将这个因式扔掉．(3)单项式乘法法例关于三个以上的单项式相乘也合用.参照答案1. 解：（ 1）不正确，（ 2）第①步出现错误，第②③步还有错误；（ 3）（ x 2+ax+b ）（ 2x 2-3x-1 ）的睁开式中含 x 3 的项有： -3x 3+2ax 3=（ 2a-3 ）x 3， 含 x 2 的项有： -x 2+2bx 2-3ax 2=（ -3a+2b-1 ）x 2． 又∵ x 3 项的系数为 -5 ， x 2 项的系数为 -6 ，2a3，a 1 5，解得 ∴有．3a 2b 1， b462. 解：（ 1）（ x+1）（ x+2）=x 2+3x+2， （ x-1 ）（ x-2 ） =x 2-3x+2 ， （ x-1 ）（ x+2） =x 2+x-2 ，（ x+1）（ x-2 ） =x 2-x-2 ；（ 2）能够发现题（ 1）中，左右两边式子切合（x+p ）（ x+q ） =x 2+（ p+q ） x+pq 结构．（ 3）由于 12 能够分解以下 6 组数， a × b=1× 12， 2× 6，3× 4，（ -1 ）×（ -12 ），（ -2 ）×（ -6 ），（ -3 ）×（ -4 ），所以 m=a+b 应有 6 个值．乘法公式专题一与乘法公式有关的规律研究题1.察看以下各式：（ x-1 ）（ x+1）=x2-1（x-1 ）（ x2+x+1）=x3 -1（x-1 ）（ x3+x2 +x+1） =x4-1（x-1 ）（ x4+x3 +x2+x+1）=x5 -1（1）你可否由此概括出一般性规律：（x-1 ）（ x n-1 +x n-2 +x n-3 + +x2+x+1）=____；（2）依据（ 1）求出： 1+2+2++262+263的结果 .2.察看下边各式规律：222 21 +（ 1× 2） +2 =（ 1×2+1）；22+（ 2× 3）2+32=（ 2×3+1）2；32+（ 3× 4）2+42=（ 3×4+1）2写出第 n 个的式子，并证明你的结论．专题二与平方差公式有关的图形问题3.以以下图，把正方形的方块，按不一样的方式区分，计算其面积，即可获得不一样的数学公式．按图 1 所示区分，计算面积，便获得一个公式：（x+y ）2=x2 +2xy+y 2．若按图 2 那样区分，大正方形则被区分红一个小正方形和两个梯形，经过计算图中的面积，请你达成下边的填空．（1）图 2 中大正方形的面积为 __________ ；（2）图 2 中两个梯形的面积分别为 __________；（3）依据（ 1）和（ 2），你获得的一个数学公式为______________________ ．5.图 1 是一个长为 2m，宽为 2n 的长方形，沿图中虚线用剪刀均匀分红四块小长方形，而后按图 2 的形状拼成一个正方形．（ 1）图2 中的暗影部分的面积为_______；_______若x+y=-6 ，（ 2）察看图2，三个代数式（m+n)2，（ m-n) 2， mn之间的等量关系是xy=，则 x-y=___________(4 ）察看图3，你能获得如何的代数恒等式呢（ 5）试画出一个几何图形，使它的面积能表示（2 2 m+n）（ m+3n） =m+4mn+3n.专题三平方差公式的逆运用5.假如一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神奇数”．如： 4=22-0 2， 12=42-2 2，20=62-4 2，所以 4， 12， 20 都是“神奇数”（1） 28 和 2 012 这两个数是“神奇数”吗为何？（2）设两个连续偶数为 2k+2 和 2k（此中 k 取非负整数），由这两个连续偶数结构的神奇数是 4 的倍数吗为何？（3）两个连续奇数的平方差（ k 取正数）是神奇数吗为何状元笔录【知识重点】1.平方差公式： (a+b) （ a-b ） =a2-b 2．用语言表达为：两数和与这两数差的积，等于它们的平方差．3. 完整平方公式：(a+b) 2=a2+2ab+b2，(a-b) 2=a2 -2ab+b 2.语言表达为：两数和（或差）的平方，【方法技巧】平方差公式常用的几种变化形式：(1) 地点变化： (b+a)(-b+a ） =(a+b)(a-b ） =a2 -b 2；(2) 符号变化：（-a-b ）（ a-b ） =- （a+b）（ a-b ） =-(a 2 2 -b ) ；(3) 系数变化： (2a+3b)(2a-3b)=4a 2 -9b 2；（4）指数变化： (a 2+b2)(a 2-b 2)=(a 2) 2-(b 2) 2=a4-b 4（ 5）增项变化：（ a-b-c)(a-b+c)=(a-b) 2-c 2,完整平方公式常有以下几种变化形式：(l)a2+b2=(a+b)2-2ab;2 2 2(2)a +b =(a-b) +2ab；(3)2ab=(a+b)2-(a2+b2);(4)2ab=(a 2+b2) -(a-b)2；(5)(a+b)2=(a-b)2+4ab；（ 6） (a-b) 2-(a+b)2=4ab.参照答案1.解：①（ x-1 ）（ x n-1 +x n-2 +x n-3 + +x2+x+1 ） =x n-1 ；②原式 =（ 2-1 ）（ 263+262+ +22+2+1） =264 -1 ．2.解：第 n 个式子： n2+[n （ n+1） ] 2+（ n+1）2=[n （n+1） +1] 2.证明：由于左侧 =n2+[n （ n+1） ] 2+（ n+1）2=n2+（ n2+n）2+（n+1）222 2=（ n +n） +2n +2n+1=（ n2+n）2+2（ n2+n） +1=（ n2+n+1）2，而右侧 =（ n2+n+1）2，所以，左侧 =右侧，等式建立3.解：（ 1）图中大正方形的面积为 x2；（ 2）两个梯形的面积分别为1（x+y）（x-y）；2（3） x2-y 2=2×1（ x+y ）（ x-y ）；即 x2-y 2=（x+y ）（ x-y ）．24.解：（ 1）（ m-n）2（2）（ m-n）2+4mn=（ m+n）2（3）± 52 2（4）（ m+n）（ 2m+n） =2m+3mn+n （5）答案不独一，比如：222 25.解：（1）28=2×14=（8-6）（8+6）=8 -6；2012=4× 503=504 -502，所以 28 和 2012 是神奇数．（ 2）（ 2k+2）2- （2k ）2=（ 2k+2-2k ）（ 2k+2+2k ）=4（ 2k+1），∴由 2k+2 和 2k 结构的神奇数是 4 的倍数．（3）设两个连续奇数为 2k+1 和 2k-1 ，则（ 2k+1）2- （ 2k-1 ）2=8k=4× 2k，∴两个连续奇数的平方差不是神奇数．整式的除法专题与乘除互逆运算有关的问题1.已知一个多项式与单项式-7x 2y3的积为 21x4y5-28x 7y4+14x6y6，试求这个多项式.2.已知被除式为x3+3x2-1 ，商式是x，余式是 -1 ，求除式．状元笔录【知识重点】1.单项式除以单项式法例：单项式相除，把系数、同底数幂分别相除后，作为商的因式；关于只在被除式里含有的字母，则连同它的指数一同作为商的一个因式，2.多项式除以单项式法例：多项式除以单项武，先把这个多项式的每一项分别除以这个单项式，再把所得的商相加，即：（ a+b+c) ÷ m=a÷ m+b÷ m+c÷ m．【温馨提示】1.计算单项式除以单项式时要注意：(1)商的符号；(2)运算次序与有理数运算次序同样．2.在进行多项式除以单项式时，必定要注意符号，不要漏除每一项．多项式除以单项式的重点是逐项去除，结果的项数与多项的项数同样，这是查验能否漏项的重要方法．注意多项式带单位对要加括号 .参照答案1.解：依题意：所求多项式=（ 21x 4y5-28x 7y4 +14x6y6）÷（ -7x 2y3） =-3x 2y2+4x5y-2x 4y3．2.解：[x3+3x2-1-（-1）]÷ x=（x3+3x2）÷ x=x2+3x．因式分解专题因式分解的奇妙应用2 21．假如 m－ n=－ 5，mn=6，则 mn－ mn的值是（）A． 30 B．－ 30 C． 11 D．－ 112．利用因式分解计算32×+×+×2013=___________．3．在以下三个不为零的式子：x2－4x， x2+2x， x2－ 4x+4 中 .（1）请你选择此中两个进行加法运算，并把结果因式分解；（2）请你选择此中两个并用不等号连结成不等式，并求其解集．状元笔录【知识重点】我们把一个多项式化成几个整式的积的形式，像这样的式子边形叫做这个多项式因式分解，也叫做把这个多项式分解因式．【方法技巧】因式分解的方法：(1)提公因式法：假如多项式的各项有公因式，能够把这个公因式提拿出来，将多项式写成公因式与另一个因式的乘积的形式，这样分解因式的方法叫做提公因式法．(2)将乘法公式的等号两边交换地点，获得用于分解因式的公式，用来把某些拥有特别形式的多项式分解因式，这类分解因式的方法叫做公式法．(3)平方差公式： a2－ b2=(a+b)(a － b) ，两个数的平方差，等于这两个数的和与这两个数的差的积．(4)完整平方公式：a2± 2ab+b2=(a ± b) 2，两个数的平方和，加上( 或减去 ) 它们的积的 2 倍，等于这两个数的和( 或差 ) 的平方．参照答案2 21． B【分析】∵ m－n=－5，mn=6，∴m n－mn=mn（m－n）=6×（－5）=－30.应选B．2． 2013【分析】32×+×+× 2013=× 2013+× 2013+× 2013=2013×（++）=2013×1=2013．3．解： (1) （ x2－ 4x） +（x2+2x）=2x2－ 2x=2x （x－ 1）．(2)x2－4x＞x2+2x，归并同类项，得－6x＞ 0，解得 x＜ 0．。

乘法公式1. 2 2 1x mx 是一个完整平方式，那么 m 的值为〔〕A、1B、－1C、1D、0２.假定a ＞０，且a 2 1a ，那么2a42a＝〔〕A、３B、－1C、－３D、５３.假定ab ＜０，那么2(a b) 与2(a b) 的大小关系是４.设x 2z 3y ，试判断 2 9 2 4 2 4x y z xz 的值能否是定值？假如是定值，求出它的值；否那么请说明原因。

５.假定2 2 2 2 2 2 2A 1 2 3 4 ...... 99 100 101 ，那么A被３除得的余数是。

6、假定x y 2， 2 2 4x y ，那么2002 2002x y 的值是：7、〔1〕计算：220042003 12 220042002 20042004〔2〕计算：2200520042 220052003 20052005 2〔3〕 3 2培优训练〔 2〕1、在多项式 29x 1中,增添一个单项式 ,使其成为一个完整平方式 .那么增添的单项式能够是 (起码填 3 种)2、a,b 知足等式 2 2 20x a b , y 4(2 b a), 请比较x, y的大小关系.3、 2 2 2 2M (x 2x 1) x 2x 1 ,N (x x 1) x x 1 ,( x 0)比较M , N 的大小关系.4、(希望杯邀请赛 ) x,y知足 2 2 5x y 2x y ,求代数式4xyx y的值 .5.计算 :1) 2 2(2 x 3y) (2 x 3y) 2)2 2 2 3(2a 1) (2a 1) (2a 3) (2a 3)6. 2(x y) 2x 2y 1 0 ，那么999 (x y) ＝7. x y 1， 2 2 2x y ，那么4 4x y 的值是〔〕A、４B、３C、72 D、528、假定a,b为有理数，且2 22a 2ab b 4a 4 0，求2 2a b ab 的值。

培优训练〔 3〕1.a 1999，b 1，那么 2 2 2 3a b ab 。

整式的乘除培优专题（学生版）一．选择题（共3小题）1．计算202020191(2)()2-⨯-等于（ ） A ．2- B ．2 C ．12- D ．122．化简(4)(1)(4)(1)x x x x +-+-+的结果是（ ）A ．228x -B ．224x x --C ．228x +D ．226x x +3．如图1，将一张长方形纸板四角各切去一个同样的正方形，制成如图2的无盖纸盒，若该纸盒的容积为24a b ，则图2中纸盒底部长方形的周长为（ ）A ．4abB ．8abC ．4a b +D ．82a b +二．填空题（共8小题）4．已知2m n +=，1mn =-，则(1)(1)m n --的值是 ．5．计算：(21)(3)x x +-的结果是 ．6．若1(3)1a a +-=，则a = ．7．设(2)(5)M x x =--，(3)(4)N x x =--，则M N ．（填<，=，)>8．若2(3)()x x px q -++的结果不含2x 和x 项，则p q += ．9．若3m x =，2n x =，则23m n x += ⋅10．如图．现有正方形卡片A 类，B 类和长方形卡片C 类各若干张，如果要拼一个长为(3)a b +，宽为(32)a b +的大长方形，那么需要C 类卡片的张数是 ．11．已知m n t y z x z x y x y z==+-+-+-，则()()()y z m z x n x y t -+-+-的值为 ．三．解答题（共9小题）12．如图，现有一块长为(4)a b +米，宽为(2)a b +米的长方形地块，规划将阴影部分进行绿化，中间预留部分是边长为a 米的正方形．（1）求绿化的面积S （用含a ，b 的代数式表示，并化简）；（2）若2a =，3b =，绿化成本为100元/平方米，则完成绿化共需要多少元？13．先化简，再求值：（1）已知：213x y ++=，求393x y ⨯⨯的值．（2）已知：23m x =，25n y =，求323211()()m n m n m n x y x y x y -++--⋅的值．14．观察下列各式2(1)(1)1x x x -+=-23(1)(1)1x x x x -++=-324(1)(1)1x x x x x -+++=-…（1）分解因式：51x -= ；（2）根据规律可得(1)x -(1n x -+…+x +1) （其中n 为正整数）；（3）计算：(31)-(504948333+++…+2331++)．15．观察以下等式：23(1)(1)1x x x x +-+=+23(3)(39)27x x x x +-+=+23(6)(636)216x x x x +-+=+…（1）按以上等式的规律，填空：()(a b + 33)a b =+（2）利用多项式的乘法法则，证明（1）中的等式成立．（3）利用（1）中的公式化简：2222()()()()x y x xy y x y x xy y +-+--++16．规定两数a ，b 之间的一种运算，记作(,)a b ；如果c a b =，那么(,)a b c =．例如：因为328=，所以(2,8)3=．（1）根据上述规定，填空：①(5,125)= ，(2,32)--= ；②若1(,)416x =-，则x = ． （2）若(4,5)a =，(4,6)b =，(4,30)c =，试说明下列等式成立的理由：a b c +=．17．已知关于x 、y 的方程组22(24x y m m x y +=⎧⎨-=⎩为常数）． （1）计算：224x y -= （用含m 的代数式表示）；（2）若236()()(x y a a a a ÷=是常数0)a ≠，求m 的值；（3）若m 为正整数，满足0||n x y <-的正整数n 有且只有8个，求m 的值．18．我们已经学习过多项式除以单项式，多项式除以多项式一般可用竖式计算，步骤如下： ①把被除式、除式按某个字母作降幂排列，井把所缺的项用零补齐；②用被除式的第一项除以除式第一项，得到商式的第一项；③用商式的第一项去乘除式，把积写在被除式下面（同类项对齐），消去相等项；④把减得的差当作新的被除式，再按照上面的方法继续演算，直到余式为零或余式的次数低于除式的次数时为止，被除式=除式⨯商式+余式，若余式为零，说明这个多项式能被另一个多项式整除．例如：计算432(671)(21)x x x x ---÷+，可用竖式除法如图：所以432671x x x ---除以21x +，商式为323521x x x -+-，余式为0．根据阅读材料，请回答下列问题：（1）32(475)(2)x x x x -+-÷-的商是 ，余式是 ；（2）32x x ax b -++能被222x x ++整除，求a ，b 的值．19．阅读以下材料：材料一：如果两个两位数ab ，cd ，将它们各自的十位数字和个位数字交换位置后得到两个完全不同的新数ba ，dc ，这两个两位数的乘积与交换后的两个两位数的乘积相等，则称这样的两个两位数为一对“有缘数对”．例如：469664694416⨯=⨯=，所以，46和96是一对“有缘数对”，材料二：在进行一些数学式计算时，我们可以把某一单项式或多项式看作一个整体，运用整体换元，使得运算更简单．例如：计算22(31)(38)x x x x +-+-，令：2(3)x x A +=，原式2222(1)(8)98(3)9(3)8A A A A x x x x =--=-+=+-++436278x x x =+-+解决如下问题：（1）①请任写一对“有缘数对” 和 ．②并探究“有缘数对” ab 和cd ，a ，b ，c ，d 之间满足怎样的等量关系．并写出证明过程．（2）若两个两位数22(23)(24)x x x x ++-+与22(25)(25)x x x x -+++是一对“有缘数对”，请求出这两个两位数．20．观察下列式子：2(1)(1)1x x x -÷-=+；32(1)(1)1x x x x -÷-=++；432(1)(1)1x x x x x -÷-=+++；5432(1)(1)1x x x x x x -÷-=++++；（1）猜想：7(1)(1)x x -÷-= ；7(21)(21)-÷-= ；（2）根据（1）猜想的结论计算：23456712222222+++++++．。