高思奥数一年级下册含答案第15讲图形剪拼
- 格式:wps
- 大小:2.10 MB
- 文档页数:12

一年级数学思维训练:《剪拼图形》所属体系板块:第二级上主要知识点:1)图形的剪分:对折、过中心点折;等分2)图形的拼组:一般先拼大图形3)图形的剪拼:在原图上找目标能力培养:动手能力,空间想象能力体系对接:第三级上图形七十二变预习题目:下面有一张正方形纸,你能把它分成四个形状、大小都一样的图形吗?你能想到几种方法呢?《剪拼图形》知识点一、图形的剪分1、等分:①对折②过中心点折【例】剪一刀使下面的正方形变成两个形状、大小一样的图形.【解析】将图形分成形状、大小一样的图形,这样的分法叫等分.等分,可以通过“对折”、“过中心点折”,折纸帮助我们找到“折痕”,沿着相应折痕剪,就可以将图形等分.剪法如下:2、二等分→四等分→八等分→……对折一次:两等分对折两次:四等分(对折三次:八等分)二、图形的拼组先找大图形,补成目标图形能拼就能分【例】用下面同样大小的两个直角三角形拼成一个平行四边形.【解析】首先要了解直角三角形和目标图形“平行四边形”的特点.拼图形,必须边对边拼,而且是一样长的边才能拼.可以拼出两种平行四边形,如下:三、图形的剪拼找目标(原图上找)【例】把下面形状的纸片剪一刀,再拼成一个正方形.【解析】观察图形,目标是正方形,可以在原图上画出目标正方形,多出的部分剪掉,补到缺的地方,即可得到目标图形.四、七巧板游戏1、认识七巧板的七个图形2、一般先拼大的,再拼特殊的《剪拼图形》课后拓展练习1、小山羊带来一个等边三角形,你能帮忙剪一刀把等边三角形变成两个形状、大小一样的图形吗?2、小蜜蜂找到了下面三种图形,你能拼成一个梯形吗?3、小蜜蜂右边有四个图形中,选哪两个可以拼成一个长方形的图形呢?4、把左边的图形剪一刀,你能拼成右边的图形么?【参考答案】:1、知识点:对折、等分2、知识点:拼图形3、知识点:拼图形,先拼大图形(1)和(3)可以拼成一个长方形.4、知识点:剪拼图形,在原图上找目标将下面的粗黑线剪开,把左边剪下来的拼到右边.。

我会比一比推理比较图形的折叠我会算一算——加法数学活动我会算一算——减法你能把下面的加法算式改成道加法算式和两道减法算式吗?你能把下面的加法算式改成一道加法算式和两道减法算式吗小动物教你学减法,一起来练一练。
小猫钓鱼算出小鱼身上算式的结果小鱼就被钓上来啦!比一比小猫钓鱼,算出小鱼身上算式的结果小鱼就被钓上来啦!比比,看谁钓的又快又多!每只小动物的车应该停在几号停车场呢?连一连。
聪明的小朋友们,你能在一分钟内口算出下面各题吗?我们来比赛吧!吗?请画出找球的线路。
生活中的数学小老虎在和小牛捉迷藏,小老虎只有从1开始按每次多2的数字往前走才能找到小牛小朋友们试试小牛。
小朋友们试一试。
小朋友们,学习了20以内加减法的计算大家都成了计算小能手的计算,大家都成了计算小能手了。
你知道加减法有什么用途呢?利用加减法可以解决生活中的许利用减可解决中的许多数学问题,这节课我们就一起看图来解决问题。
⑴根据下面的图写算式⑴根据下面的图写算式。
⑵根据下面的图写算式⑵根据下面的图写算式。
说一说每个图表示什么意思然后写出算式说说每个图表示什么意思,然后写出算式。
看图填空,并列出算式。
⑴⑵聪明的小朋友,你知道下面每幅图的意思吗?请你根据图意写出算式。
⑴原来有11只兔子。
我已经卖出去了5只。
还剩下几只没有卖出去?棵花还有棵没有栽已经栽了多少棵了?⑵一共要栽14棵花。
还有4棵没有栽。
已经栽了多少棵了?你能根据下面的图列出算式吗?⑴⑵原来车上有15人。
草地上原来有15只白兔子和7只灰兔子,后来又跑来了4只灰兔子,跑走了5只白兔子。
你能跟据下面不同的问题列出不同的算式吗?⑴草地上原来共有几只兔子?⑵草地上现在有几只白兔子?⑶草地上现在有几只灰兔子?比一比,算一算。
⑴小明折了多少架纸飞机?12个同学排成一队去游玩,小明的后面有3个同学,他的前面有几个同学?钟面上的数学钟面上有时针、分针和12个数字。
短而粗的是时针,长而细的是分针。
钟面上把一圈平均分成12个大格,每个大格又分成相等的5个小格,分针走一圈是分钟;时针走一圈是分针走圈是60分钟;时针走圈是12小时。

1、请你准备一张长方形纸,按下面要求剪一剪。
① 将这个长方形剪一刀,剪成两个形状和大小一样的图形。
② 将这个长方形剪两刀,剪成四个形状和大小都一样的图形。
2、请你把下面的正方形分成形状、大小一样的 2 份,有几种分法?
3、我会剪图形。
① 将下面的正三角形剪成 2 个形状、大小一样的三角形。
② 将下面的正三角形剪成 4 个形状、大小一样的三角形。
4、你能把下面的图形剪一刀再拼一拼,拼成长方形吗?
5、请把下面的图形剪 2 刀,变成 3 块,然后再拼成一个正方形。
6、把下面的图形剪 2 刀,然后拼成一个正方形。
7、下面的图形各是由几个同样大小的小三角形拼成的?
8、把下图划分成大小形状都相同的三部分,而且每部分要求要有一个圆圈。
9、下面两个图形,可以分割成 4 个大小相等,形状相同的图形。
下面 A、B、
C、D 四个选项中的哪个图形?
10、你能把下面的图形分割成 4 个形状相同、大小相等的图形吗?
1、【答案与解析】
等分过中心即可!
①
②
2、【答案与解析】
3、【答案与解析】
①②
4、【答案与解析】
5、【答案与解析】
6、【答案与解析】
分法不唯一,只要能拼成正方形的都可以。
7、【答案与解析】 6 个,10 个,8 个
8、【答案与解析】
9、【答案与解析】选择 D
10、【答案与解析】。

第十五讲图形规律初步前续知识点:一年级第一讲;XX模块第X讲后续知识点:X年级第X讲;XX模块第X讲君⑨阿呆和阿瓜也忌迫後子'穴泉笑的前仰肓伏阿瓜莉娅:把相应的人物换成红字标明的人物.图形是数学中的一个重要分支,把数和图形结合起来,可以从中获取有用的信息,较好地激发再造性想象,实现形象思维与抽象思维的互助互补、相辅相成.寻找图形规律是解决数学问题中的一种重要手段,通过归纳图形变化,培养敏锐的观察力和严密的逻辑推理能力.(1)▲ ▲ ▲ ▲ ________________________________⑵,、二 U U I. .(3) -------------------------【提示】仔细观察每组图形的规律.图形推理的两大灵魂:数量关系和图形的转动•寻找图形变化规律,可以有意识的从图形的移动、旋转、周期以及数量等变化角度来思考.找出下列图形的排列规律,再接着画4个图形.(2)例题2请你按照前面图案的变化规律,画出第4个图案.【提示】画出每组的第1个图,动手转一转.练习2在下面的各图案中,涂色的部分是按一定方向转动的•请按照规律,补全最后一个图案.⑴㊉㊉㊉㊉例题3iQfC/ ■■■■找到下列图案的排列规律,补全缺少部分的图案.【提示】同心圆的位置发生了什么变化?(1)(2)f<4•—□T-o](2)找到下列图案的排列规律,补全缺少部分的图案.O△□☆☆O△□□☆O△例题4请你根据前3个方框中字母的变化规律,补全第(1)(2) A B C D E B C D E AA B C D E B D C E AC D E A BD E C A B4个方框.【提示】观察A的位置变化.练习4△▲0・口・O•口请你根据前3个方框中图形的变化规律,补全第4个方框.例题5找到下列图案的排列规律,补全缺少部分的图案.?找出下列图形的排列规律,补全“?”处的图形X XZ□nK?【提示】每行图形之间有规律吗?星期的来历“星期”就是星的日期的意思•现在通用的以7天为一星期的制度,产生于古代西亚的两河流域•公元前7至6世纪,亚述帝国和新巴比伦王国时期,巴比伦人便有了星期制.他们把一个月分为4周,每周有7天,即为一个星期•这是因为巴比伦人有一座祭祀星神的建筑,共7层,称作7星坛•从上到下依次为日、月、火、水、木、金、土7个星神,巴比伦人认为这7个星神是轮流值日的,各主管一天,他们每一天祭祀一个神,7天为一个周期,而且每一天都以一个星神的名字命名.太阳神沙玛什主管星期日,称为日曜日;月神南纳主管星期一,称为月曜日;火星神吉比尔主管星期二,称为火曜日;水星神纳布主管星期三,称为水曜日;木星神马尔都克主管星期四,称为木曜日;金星神伊什塔尔主管星期五,称为金曜日;土星神尼努尔达主管星期六,称为土曜日.巴比伦人创立的星期制,首先传到希腊罗马等古代世界各地•公元321年3月7日,君士坦丁大帝正式宣布7天为一星期,形成定律后一直相沿至今•一星期又称为一礼拜,这是后来基督徒把一星期作为参拜上帝的宗教仪式的周期,故称为“礼拜”作业1.找出下列图案的排列规律,再接着画出 4个图形.(2) _______________________________________________________________________________2.请你根据前3个图案的变化规律,画出第 4个图案.O O △ □ □ O△△ O4.请你根据前3个方框中图形的变化规律,补全第 4个方框.(1)(2)•□■△▲O O •口 ▼▽★☆♦◊♦◊▼▽★☆3.5.找出下列图案的排列规律,补全缺少部分的图案.12.第十五讲图形规律初步1.例题1答案:▲ ▲ ;—] ——;• ★详解:属于最简单的形状变化规律和颜色规律.第一列图形的排列规律是△和▲为一组循环出现•第二列图形的排列规律是□为一组循环出现•第三列图形的排列规律是★为一组循环出现.2.例题2答案:详解:属于典型的旋转规律•做旋转规律的题一定要找到一个固定的参考位置,以参考位置变化为准•第一排参考位置可以选取笔的尖端,是顺时针旋转规律,第二排可以选取黑点为参考,所以是顺时针规律.3.例题3答案:详解:属于有序移位型问题•可以把图形同心圆当作参考位置•图形同心圆第一排在最后一个位置,第二排在最后位置的前一个位置,第三排则又往前面移动一个位置.4.例题4答案:B C D E A ; E A C B D详解:属于有序移位型问题•观察两列字母的移动规律.5.例题5答案:详解:属于组合规律问题•第一列图形与第二列中不同位置的球组合形成第三列图形.6.例题6答案:详解:第三列是第一列和第二列图形不同点的集合.7.练习1答案:8. 练习2简答:旋转规律•以蓝色的块作为参考位置,找到蓝色块的移动规律.9. 练习3答案:△ □☆O简答:以o 作为固定参考对象,观察它的位置变化发现:第一排的第 个;同时,第一排的第 1个图形变成第二排的第 2个•以此类推10. 练习4答案:简答:属于有序移位型问题•观察□的位置.11. 作业1答案:(1)( 2)_简答:第一行的规律是两个图案:工狩:.循环,按照图案的排列顺序画 三个图案 ^on 循环,按照图案的排列顺序画 4个图案.作业2答案:(1) 简答:观察两个图案的变化规律,其变化规律均为按顺时针方向进行旋转,按照这个规律补全图 案. 4个图形在第二排时移到第 1 4个图案.第二行的规律是简答:按照一定顺序排列,缺什么补什么.答案: (2)13.作业3答案:O△□□O△△□O简答:每一行、每一列都有O、△和□三个图形,且各出现一次,只要找出缺失项就好.14.作业4答案:(1)(2)简答:第一行规律是:最后一个图形移至最前,其他图形依次向后推移.第二行规律是:最后两个图形移至最前,其他图形依次向后推移.15.作业5答案:简答:观察发现每行的第一列和第二列的黑色方块结合在一起,组成第三列的图案.12.。


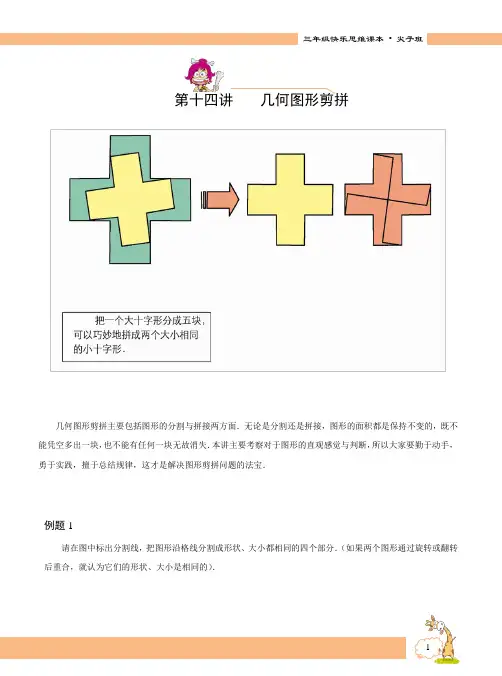
图形的折叠、剪拼与分割一页普通的纸,童年时我们用稚气的双手把它折成有趣的动物,民间艺人可以把它剪成美丽的图案.折纸与剪纸是最富于自然情趣而又形象生动的实验,是丰富想象力与心灵手巧的结合.对图形进行折叠与剪拼,是学习几何不可或缺的重要一环,通过折叠与剪拼图形,我们可以发现一些几何结论并知晓这些结论是怎样被证明的.把图形或部分沿某直线翻折叫图形的折叠,对图形通过有限次的剪裁再重新拼接成新的图形叫图形的剪拼.解与图形折叠或剪拼相关的问题,利用不变量解题是关键,在折叠过程中,线段的长度、角的度数保持不变;在剪拼过程中,新图形与原图形的面积一般保持不变.例题求解【例1】如图,有一块直角三角形纸片,两直角边AC=6㎝,BC=8㎝,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于.(南通市中考题)思路点拨设CD=x,由折叠的性质实现等量转换,将条件集中到Rt△BDE中,建立x的方程.注图形折叠与剪拼问题可考壹我们的动手操作能力和分析推理能力,解题时需要把计算、推理与合情想象结合起来.折叠问题可以对称观点认识:(1)折痕两边是全等的;(2)对应点连线被折痕垂直平分.解折叠问题常用到勾股定理、相似形、方程思想等知识与方法.【例2】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为( ) A.12 D10 C.8 D.6 (2004年武汉市选拔赛试题)思路点拨只需求出AF长即可.【例3】取一张矩形的纸进行折叠,具体操作过程如下:第一步:先把矩形ABCD对折,折痕为MN,如图1;第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B′,得Rt△AB'E,如图2;第三步:沿EB'线折叠得折痕EF,如图3.利用展开图4探究:(1)△AEF是什么三角形?证明你的结论.(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.(山西省中考题)思路点拨本例没有现成的结论,需经历实验、观察、猜想、证明等数学活动,从而探究得到结论.【例4】如图,是从边长为40cm、宽为30cm的矩形钢板的左上角截取一块长为20cm、宽为10cm的矩形后,剩下的一块下脚料.工人师傅要将它作适当地切割,重新拼接后焊成一个面积与原下脚料的面积相等,接缝尽可能短的正方形工件.(1)请根据上述要求,设计出将这块下脚料适当分割成三块或三块以上的两种不同的拼接方案(在图2和图3中分别画出切割时所沿的虚线,以及拼接后所得到的正方形,保留拼接的痕迹);(2)比较(1)中的两种方案,哪种更好一些?说说你的看法和理由.(山东省中考题)思路点拨 拼接后正方形的边长为221030 ㎝,它恰是以30cm 和10cm 为两直角边的直角三角形的斜边的长,为此可考虑设法在原钢板上构造两直角边长分别为30㎝和l0cm 的直角三角形,这是解本例的关键. 注 有效的数学学习过程不能单纯地依赖模仿与记忆,应该通过观察、实验、操作、猜测、验证、推理等数学活动,形成自己对数学知识的理解和有效的学习策略,从而使知识得到内化,形成能力. 近年中考中涌现的设计新颖、富有创意的折叠、剪拼与分割等问题,注重对动手实践操作、应用意识、学习潜能的考查.【例5】 用10个边长分别为3,5,6,11,17,19,22,23,24,25的正方形,可以拼接成一个矩形.(1)求这个矩形的长和宽; (2)请画出拼接图.思路点拨 利用拼接前后图形面积不变求矩形的长和宽;运用矩形对边相等这一性质画拼接图. 【例6】 如图,已知△ABC 中,∠B=∠C=30°,请设计三种不同的分法,将△ABC 分割成四个三角形,使得其中两个是全等三角形,而另外两个是相似但不全等的直角三角形.请画出分割线段,标出能够说明分法的所得三角形的顶点和内角度数(或记号).(画图工具不限,不要求证明,不要求写出画法) (温州市中考题)思路点拨 充分运用几何计算、推理和作图,综合运用动手操作、空间想象、解决问题.学力训练1. 将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到 条折痕,如果对折n 次,可以得到 条折痕.(2002年南宁市中考题)2.一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A 、B 重合,若∠B=30°,AC=3,则折痕DE 的长等于 . (三明市中考题)3.如图,将一块长为12的正方形纸片ABCD 的顶点A 折至DC 边上的点E ,使DE =5,折痕为PQ ,则线段PM= .4.在△ABC 中,已知AB=20,∠A=30°,CD 是AB 边的中线,若将△ABC 沿CD 对折起来,折叠后两个小三角形ACD 与三角形BCD 重叠部分的面积恰好等于折叠前△ABC 的面积的41,有如下结论:①AC 边的长可以等于a ;②折叠前的△ABC 的面积可以等于223a ;③折叠后,以A 、B 为端点的线段AB 与中线CD 平行且相等,其中,正确结论有 个. (天津市中考题)5.将四个相同的矩形(长是宽的3倍),用不同的方式拼成一个大矩形,设拼得大矩形的面积是四个小矩形的面积和,则大矩形周长的值只可能有( )A .1种B .2种C .3种D .4种 (2003年南昌市中考题)6.如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,则∠A 与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( ) A .∠A=∠1+∠2 B .2∠A =∠1+∠2 C .3∠A =2∠1+∠2 D .3∠A=2(∠l+∠2) (北京市海淀区中考题)7.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①、②两部分.将①展开后得到的平面图形是( )A .矩形B .三角形C .梯形D .菱形 (陕西省中考题)8.如图1,小强拿一张正方形的纸,沿虚线对折一次得图2,再对折一次得图3,然后用剪刀沿图3中的虚线剪去一个角,再打开后的形状是( ) (济南市中考题)9.如图,东风汽车公司冲压厂冲压汽车零件的废料都是等腰三角形的小钢板,其中AB=AC,该冲压厂为了降低汽车零件成本,变废为宝,把这些废料再加工成红星农业机械厂粉碎机上的零件,销售给红星农业机械厂,这些零件的形状都是矩形.现在要把如图所示的等腰三角形钢板切割后再焊接成两种不同规格的矩形,每种矩形的面积正好等于该三角形的面积,每次切割的次数最多两次(切割的损失可忽略不计).(1)请你设计两种不同的切割焊接方案,并用简要的文字加以说明;(2)若要把该三角形废料切割后焊接成正方形零件(只切割一次),则该三角形需满足什么条件? (十堰市中考题)10.如图,ABCD是矩形纸片,E是AB上一点,且BE:EA=5:3,EC=155,把△BCE沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点为F,求AB、BC的长.11.如图,在△ABC中,AB=3,AC=4,BC=5,现将它折叠,使点B与点C重合,则折痕的长是. (四川省竞赛题)12.如图,一张矩形纸片沿BC折叠,顶点A落在点A,处,第二次过A,再折叠,使折痕DE∥BC,若AB=2,AC=3,则梯形BDEC的面积为.( “宇振杯”上海市竞赛题)13.如图,将矩形ABCD的四个角向内折起,恰好拼成既无缝隙又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AD与AB的比等于. ( “希望杯”邀请赛试题)14.要剪切如图l(尺寸单位mm)所示的两种直角梯形零件,且使两种零件的数量相等.有两种面积相等的矩形铝板,第一种长500mm,宽300mm(如图2);第二种长600mm,宽250mm(如图3);可供选用.(1)填空:为了充分利用材料,应选用第种铝板,这时一块铝板最多能剪甲、乙两种零件共个,剪出这些零件后,剩余的边角料的面积是 mm2.(2)画图,从图2或图3中选出你要用的铝板示意图,在上面画出剪切线,并把边角余料用阴影表示出来.15.如图,EF为正方形ABCD的对折线,将∠A沿DK折叠使它的顶点A落在EF上的G点,则∠DKG为( ) A.15° B.30° C.55° D.75°16.某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形彩条,如图,在Rt△ABC的长都不小于5cm ,则每张直角三角形彩纸能裁成的矩形纸条的总数是( )A .24B .25C . 26D .27 (山东省济南市中考题)17.如图,若将左边正方形剪成四块,恰能拼成右边的矩形,设a =1,则这个正方形的面积为( )A .2537+ B .253+ C .251+ D .2)21(+ (2003年山东省竞赛题)18.如图,已知Rt △ABC 中,∠C =90°,沿过点月的一条直线BE 折叠这个三角形,使点C 落在AB 边上的点为D ,要使点D 恰为AB 的中点,问在图中还需添加什么条件? (1)写出两个满足边的条件; (2)写出两个满足角的条件;(3)写出一个满足除边角以外的其他条件. (黄冈市竞赛题)19.如图,正方形纸片ABCD 中,E 为BC 的中点,折叠正方形,使点A 与点E 重合,压平后,得折痕MN ,设梯形ADMN 的面积为S 1,梯形BCMN 的面积为S 2,求21S S 的值20.已知一个三角形纸片ABC ,面积为25,BC 的长为l0,∠B 、∠C 都为锐角,M 为AB 边上的一动点(M 与A 、B 不重合),过点M 作MN ∥BC 交AC 于点N ,设MN=x . (1)用x 表示△AMN 的面积;(2)△AMN 沿MN 折叠,使△AMN 紧贴四边形BCNM(边AM 、AN 落在四边形BCNM 所在的平面内),设点A 落在平面BCNM 内的点A ′,△A ′MN 与四边形BCNM 重叠部分的面积为y . ①用的代数式表示y ,并写出x 的取值范围.②当x 为何值时,重叠部分的面积y 最大,最大为多少?。

第十五讲图形剪拼这个很容易,你们看,这块地是正方这 大么 阿瓜 阿呆 萱萱 小高 地方 我们 8,— Ifc.种个 人 四 树 怎么分3 配呀? 6小高形的,我们把它平均分成4块,然后每人负责一块地方就可以了.前续知识点:一年级第一讲;XX模块第X讲后续知识点:X年级第X讲;XX模块第X讲的把相应的人物换成红字标明的人物.在前面的学习中,我们已经认识了很多的图形,如果将我们已经认识的图形拼一拼、剪一剪,它们会变成什么图形呢?看看我们自己能够想到多少种不同的方法.例题1用4个完全相同的小正方形,可以拼成哪些不同的平面图形呢?拼一拼,画一画.【提示】自己动手拼一拼.练习1如图,有4个完全相同的三角形,用它们可以拼成哪些平面图形呢?拼一拼,画一画.例题2把下面的正方形分成形状相同、大小相等的示)4个图形,可以怎么分?(用虚线表【提示】把正方形折一折.练习2把一张形状为“ L”的纸,剪成4个形状相同、大小相等的图形•你有几种剪法?(用虚线表将认识的图形剪成形状相同、大小相等的图形有多种方法•但在有限制条件的情况下应该如何考虑呢?一起动手试一试.例题3请把下面的正六边形分割成4个形状相同、大小相等的图形,使每个图形中都含有一个小朋友.【提示】要保证小朋友的完整.练习3请把下面的图形分割成4个形状相同、大小相等的图形,使每个图形中都含有一个蘑菇娃娃.例题4 请把下面的长方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一只小青蛙.【提示】一共有12个格子,分割成4个形状相同、大小相等的图形,每个图形应该有几个格子呢?练习4 请把下面图形分割成4个形状相同、大小相等的图形,使每个图形中都含有一只小老虎.例题5 请把下面的正方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一只小猫.【提示】紧挨着的相同的动物一定是要隔开的.例题6请把下面的正方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一只小鸟和一条小鱼.【提示】4个形状相同、大小相等的图形可以是这样的吗?3.请把下面的长方形分割成 4个形状相同、大小相等的图形,使每个图形中都含有一个★.四巧板由下图中的四块拼板组成.拼一拼,看看下面的图形是不是由这四块板拼成的?你能自己拼出下列图形吗?作业1.如图,有4个完全相同的三角形,用它们可以拼成哪些不同的平面图形呢?在右边的方框中画一画.2.请把下面的长方形剪成形状相同、大小相等的 4个图形.(用虚线表示)课外阅读四巧板» I 1 1 1 :★: 1ll 1 1 i i★ 1 i i i :★: ■■■■■■■J 1 II 1 1 : :★4. 请把下面的正方形分割成 4个形状相同、大小相等的图形,使每个图形中都含有一个☆.II « II I " I: :☆: ☆ i ■II 5. 把下面的正方形分割成 4个形状相同、大小相等的图形,使每个图形中都含有一个☆和一个★.★■ I ■ I --- r ------1I 1★ ☆ I I I 1* II V ☆☆■Ii I»I★★☆4个形状相同、大小相等的图形,使每个图形中都含有一个☆. ☆☆4个形状相同、大小相等的图形,使每个图形中都含有一个☆和一个★.★☆☆☆4. 请把下面的正方形分割成5. 把下面的正方形分割成4. 请把下面的正方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一个☆.☆☆5. 把下面的正方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一个☆和一个★.★★☆★☆☆☆★★☆4. 请把下面的正方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一个☆.☆☆5. 把下面的正方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一个☆和一个★.★★☆★☆☆☆★★☆4. 请把下面的正方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一个☆.☆☆5. 把下面的正方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一个☆和一个★.★★☆★☆☆☆★★☆。

实用标准文档2021年四年级数学思维训练:几何图形剪拼1.如图,将一个正方形纸片剪成形状、大小都相同的四块,可以怎么剪?请大家画出尽量多的方法.〔如果两个图形通过旋转或翻转后重合,就认为它们的形状、大小是相同的〕2.观察图,ABCDEF是正六边形,O是它的中心,画出线段PQ后,就把正六边形ABCDEF分成了两个形状、大小都相同的五边形.能否画出3条线段,把正六边形分成6个形状、大小都相同的图形?能否画出几条线段,把正六边形分成3个形状、大小都相同的四边形?能否画出几条线段,把正六边形分成3个形状、大小都相同的五边形?3.如图,在一块正方形纸片中有一个正方形的空洞.现在要求用一条经过大正方形中心点的线段,把纸片分成面积相等的两局部,应该怎么办?4.请把图中的两个图形分别沿格线剪成四个形状、大小都相同的图形.5.请把图沿格线分成形状、大小都相同的三局部,使得每局部都恰好含有一个“○〞.6.如图,三角形和六角星的每条边长都相等,那么用多少个三角形可以拼成六角星?请在图中表示出来.文案大全实用标准文档7.图1是由五个相同大小的小正方形拼成的,图2是一个正方形和一个等腰直角三角形拼成的.请把这两个图形分别剪成四个形状、大小都相同的图形.8.如图,请把一个大正方形分割为两种面积不同的小正方形.〔1〕如果要求两种小正方形一共有6个,应该怎么分?〔2〕如果要求两种小正方形一共有7个,应该怎么分?9.如图,有两个面积相等的正方形纸片,现在想把它们剪拼成一个更大的正方形,要求如下:1〕如果分别剪开这两个正方形,再拼接成一个大正方形,应该怎么办?2〕如果只允许剪开一个正方形,再拼接成一个大正方形,应该怎么办?10.如图是由假设干个小正方形组成的图形,你能将其剪成两块,然后拼成一个正方形吗?11.请在图中标出分割线,把下列图沿格线分成形状、大小都相同的四个局部,〔如果两个图形通过旋转或翻转后重合,就认为它们的形状、大小是相同的〕12.把图沿格线分割成形状、大小都相同的四个局部,请在图中画出具体的分割方法.文案大全实用标准文档13.将图分割成形状、大小完全相同的四块,请至少画出4种不同的分法.14.一个边长是7厘米的正方形纸片,最多能裁出多少个长是4厘米,宽是1厘米的纸条,请画图说明.15.将图分成大小、形状都相同的四块,使得每一块中都有A、B、C、D.16.将边长分别是3厘米和4厘米的两个正方形切割成四块,然后将它们拼成一个边长是5厘米的大正方形.〔先在左下列图画出切割示意图,后在右下列图画出新拼成的正方形示意图.〕17.请将图剪成三块,再拼成一个正方形.18.将图分割成四个形状和大小都相同的局部,然后将它们拼接成一个正方形,请在原图上标明分割线,并画出正方形的拼接图.19.如图中长方形的长和宽分别是9厘米和4厘米,请把这个长方形剪成两块再拼成一个正方形.文案大全实用标准文档20.有一张长方形纸片,按图所示剪成了三块,这三块纸片可拼成一个正方形,那么正方形的边长为多少?请画出具体的拼法.21.把七个长为4厘米、宽为3厘米的长方形既互不重叠又不留空隙地拼成一个大长方形,那么这个大长方形的周长最小是多少厘米?请画出具体的拼法.22.用假设干个边长为1、2、3、4的正方形纸片互不重叠地拼成一个边长为5的大正方形,那么最少需要纸片多少张?请画出具体的拼法.23.将图沿格线分割成大小、形状完全相同的四个局部,你能想出几种方法?〔如果两个图形通过旋转或翻转后重合,就认为它们的形状、大小是相同的〕24.如图,长方形的长和宽分别是25厘米和16厘米.请把这个长方形剪成两块,再拼成一个正方形.25.如图1是一块25×49〔单位:厘米〕的长方形纸片,现在要沿虚线将它分成三块,再拼成图2的边长为35厘米的正方形纸片.请用实线标明剪切和拼接的方法,在这里,虚线划分成的小长方形的大小均为5×7〔单位:厘米〕.26.将图沿格线分割成七个形状不同的长方形〔包含正方形〕,请在图中用实线标出分割线.文案大全实用标准文档27.如图是由5个小正方形组成的一个“十字架〞.请将它剪成假设干块,然后拼成一个大正方形.28.如图,一个大长方形左上角缺少一个2×3的小长方形.请把这个图形分成三局部,再拼成一个正方形.29.有一个大正方形,现在要把它分割为12个小正方形,那么:〔1〕要形成2种面积不同的小正方形,可以如何分割?〔2〕要形成3种面积不同的小正方形,可以如何分割?〔3〕要形成4种面积不同的小正方形,可以如何分割?30.请画出一个三角形,并把它分成大小形状都完全相同的4个小三角形.如果要分为完全相同的16个小三角形,该如何画?文案大全实用标准文档参考答案1.比拟常见的方法:【解析】试题分析:前三种是比拟常见的方法,又因为正方形是中心对称图形,根据中心对称的性质,正方形一定被经过中心的直线平分据此解答即可.解:比拟常见的方法:因为只是要求分成形状、大小都相同的四个局部,没要求具体什么图形,所以只要这两条直线过正方形中心且相互垂直即可,因而有无数种剪法:点评:此题考查了中心对称及正方形的性质,解决此类问题,要充分考虑题意的要求.2.根据分析画图如下:【解析】试题分析:不管把六边形平均分成几局部,六边形的六条边必须在分成的每一局部的外沿,其他边不可能在六边形的外边,只能处在六边形的内部,从这个角度来计算,分成的每一部分保存的六边形原来边的条数是:图〔2〕,分成6个形状、大小都相同的正三角形,含有原来边的条数是:6÷6=1条,相当于1条边的长度,所以连接它的中心O,和六个顶点,即可符合要求;图〔3〕分成3个形状、大小都相同的四边形,含有原来边的条数是:6÷3=2条,相当于2条边的长度,这就有两种可能,一是:相邻的两条边的长度,二是:相邻的3条边,其中两文案大全实用标准文档条边的长度各取一半,所以只有前者才可满足条件.图〔4〕把正六边形ABCDEF分成3个形状、大小都相同的五边形,含有原来边的条数是:6÷3=2条,相当于2条边的长度,这就有两种可能,一是:相邻的两条边的长度,二是:相邻的3条边,其中两条边的长度各取一半,所以只有后者才可满足条件.解:根据分析画图如下:点评:此题要从平均分成的每一局部图形的特征和规律入手,找到每一局部图形保存原有的边的长度.3.如下图:【解析】试题分析:这两个图形都是中心对称图形,找出两个图形的对称中心,过这两个中心做直线,即可把纸片分成面积相等的两局部.解:如下图:点评:解答此题需结合图形,利用中心对称图形的性质即可解决问题.4.把图分成四个大小相等、形状相同的图形如下列图:【解析】试题分析:〔1〕第一个图共12个小方格,要分成四个大小相等,形状相同的图形,每个图形应由12÷4=3个小方格组成;通过观察,画图即可;〔2〕第二个图共12个三角形,要分成四个大小相等,形状相同的图形,每个图形应由12÷4=3个三角形组成;进而分析画出即可;解:把图分成四个大小相等、形状相同的图形如下列图:文案大全实用标准文档点评:此题应结合题意,根据各图的特点,进行分析,然后试画,进而得出问题答案.5.答案如图,【解析】试题分析:此题需要认真的观察,共有12个小正方形,说明4个一组,根据图形的特点,分成正规的小正方形是不可能的,因此只能分成不规那么的图形,方案如下.解:答案如图,点评:此题应结合题意进行分析,分析过程中最好通过实践操作得出问题答案,并进行验证.6.12个,如下图:【解析】试题分析:观察图形,先把六角形的外部的六个角分割出6个与小三角形完全相同的三角形,那么内部是一个正六边形,再把正六边形的六个顶点分别与正六边形的中心连接起来,又可以分割成6个与小三角形完全相同的三角形,所以拼成这个六角形,一共要6+6=12个小三角形,据此即可解答.解:根据题干分析可得,拼成这个六角形,一共要6+6=12个小三角形,文案大全实用标准文档故答案为:12.点评:根据六角形的特点,先把这个图形进行分割,即可解答问题.7.如下图:红线为切割线:1〕2〕【解析】试题分析:〔1〕因为给出的是五个正方形拼成的图形,所以要将图形切分成四块形状、大小都一样的图形,也就是必须把这5个正方形平均分成四份,所以要把其中的正方形切割完成,如下列图.〔2〕设正方形的面积为2,那么△BEC的面积为1,根据题意,分成的每一个直角梯形的面积为,然后找出正方形的中心O,过中心O分别作OF∥AD交AB于点F、作OG∥CD交BE于点H,交BC边于点G,连接OD、HE,即可作出.解:如下图:红线为切割线:〔1〕2〕点评:〔1〕解答此题的关键是如何将五个正方形平均分成四份,由此根据图形的特点进行分割.2〕此题主要考查了复杂作图,根据面积确定出从正方形的中心入手求解是解题的关键,难度中等,但不容易考虑.8.〔1〕文案大全实用标准文档2〕【解析】试题分析:〔1〕将大正方形方的边长平均分成3等份,那么可将大正方形分割为9个相等的小正方形,其中4个相邻的组成1个,其余5个小的各成1个.2〕将大正方形方的边长平均分成4等份,分成3个2×2,4个1×1即可.解:〔1〕2〕点评:此题考查了学生实际操作以及空间想象能力.9.:如下图:1〕(2〕文案大全实用标准文档【解析】试题分析:〔1〕分别剪开这两个正方形的对角线,各分成两个直角三角形,把这两个三角形拼成一个大三角形,这样就把四个小直角三角形拼成了两个大直角三角形,再拼成正方形即可.2〕沿对角线切开,分成四个三角形,把四个三角形拼成一个菱形,找出菱形各边中点,连结即可.解:如下图:1〕2〕点评:此题考查了图形的拆拼,正确分析图形,做题时最好是先结合实物进行分割,进行观察,然后选出最正确答案.10.如图:文案大全实用标准文档【解析】试题分析:因为正方形的四条边都相等,四个角都是直角,所以根据给出的图的特点,进行如下切割和重新拼组为正方形如下.解:如图:点评:此题主要考查了学生的拼组的能力,要根据给出的图形的特点和正方形的特点解答.11.作图如下【解析】试题分析:因为共有16个方格,分成形状、大小都相同的四个局部,那么每个局部就有4个方格,根据原图形状,可分成4个“L〞形的图形,解决问题.解:作图如下点评:仔细观察图形,根据图形特点,结合“如果两个图形通过旋转或翻转后重合,就认为它们的形状、大小是相同的〞即可作出图形.12.【解析】试题分析:因为共有24个三角形,沿格线分割成形状、大小都相同的四个局部,每局部包括6个三角形,由此进行划分即可.解:文案大全实用标准文档点评:此题考查了图形的拆拼,明确每局部包括6个三角形,是解答此题的关键.13.【解析】试题分析:将图分割成形状、大小完全相同的四块,即每个图形的面积占整个图形面积的,结合图形,进行分割即可.解:点评:此题要抓住“把该图形要分割成四个大小相等、形状相同的图形,〞这条信息,从中得出每个图形要占整个图形面积的是顺利分割的突破口.14.最多能剪出12个这样的长方形.【解析】试题分析:根据题干中图形的剪切方法可得:在正方形的每条边长上,可以剪出一个长边4厘米,剩下的3厘米可以截成3条1厘米的宽边,如此一共可以剪出3+3+3+3=12个出4厘米、宽1厘米的小长方形,据此即可解答问题.解:根据题干分析可得,最多能裁出3+3+3+3=12个这样的长方形:文案大全实用标准文档答:最多能剪出12个这样的长方形.点评:此题利用画图的方法解答更简单、直观,此题也可以利用面积公式解答:7×7÷〔4×1〕≈12〔个〕.15.根据分析,分割如下:【解析】试题分析:因为每一块中都要带有A、B、C、D各一个.根据A、B、C、D的位置特点,先把A、B、C、D划分出四个局部,再根据A、B、C、D的位置特点将中图形划分出四个完全相同的四个图形即可.解:根据分析,分割如下:点评:此题主要考查图形的划分,要结合A、B、C、D的位置特征进行划分.16.如下列图所示,即可将这两个正方形拼组成一个边长为5厘米的大正方形:文案大全实用标准文档【解析】试题分析:大正方形不动,把小正方形切割成宽为1厘米的三局部,即可拼组成一个边长为5厘米的正方形.解:如下列图所示,即可将这两个正方形拼组成一个边长为5厘米的大正方形:点评:抓住正方形的特点进行讨论拼组.17.【解析】试题分析:依据图示可得:原图中可分为上面边长为3的正方形,以及下面边长为4的正方形,假设想把原图分成三块再拼成正方形,拼成正方形的边长一定不能是两个正方形的边长,且一定大于4,故此只能把原图中边长是7的边分开,据此即可解答.解:点评:此题比拟抽象,也比拟难以找出突破口,分图时不要仅仅局限于原图的边长,要根据文案大全实用标准文档具体情况进行重组.18.拼成的正方形的边长为6,画图分割如下:【解析】试题分析:我们不难技术处题中图形的面积为36,因为36=6×6,所以拼成的正方形的边长为6,由此画出正方形的拼接图.解:2×3+6×〔2+1+1〕+2×3=6+24+6=36因为36=6×6,所以拼成的正方形的边长为6,画图分割如下:点评:此题考查了图形的切拼,通过分析、计算得出拼成的正方形的边长为6,是解答此题的关键.19.如图分割即可:【解析】试题分析:长和宽分别为9厘米和4厘米的长方形,它的面积为36平方厘米,剪拼后的正方形的面积也应该是36平方厘米,它的边长为6厘米;由此把长方形的面积平均分成36份,然后分成2局部,并且使两局部的形状一样即可.解:9×4=36〔平方厘米〕,因为6×6=36,所以剪拼后的正方形的面积也应该是36平方厘米,它的边长为6厘米;如图分割即可:文案大全实用标准文档点评:此题考查了图形的切拼,明确剪拼后的正方形的面积是36平方厘米,它的边长为6厘米,是解答此题的关键.20.拼成的正方形的边长为12,拼接如下:【解析】试题分析:因为长方形的面积=长×宽,由此即可求出长方形的面积,为:〔12+4〕×9=144,因为:12×12=144,所以拼成的正方形的边长为12,由此根据给出的图形,把三块进行拼接即可.解:〔12+4〕×9=144,因为:12×12=144,所以拼成的正方形的边长为12,拼接如下:点评:此题考查了图形的切拼,明确拼成是正方形的边长是12,是解答此题的关键.21.由以上分析,周长最小的拼法如下图:周长为:38厘米.【解析】试题分析:可以拼成3种,其周长分别是:38cm,50cm,62cm.周长最小的拼法是:3个长方形横着拼接成12厘米乘3厘米的长方形,剩下的4个长方形竖着拼成12厘米乘4厘米的长方形再把这两个长方形拼成12厘米乘7厘米的长方形.这个长方形的周长是38厘米.解:由以上分析,周长最小的拼法如下图:文案大全周长为:〔4×3+3+4〕×2=19×2=38〔厘米〕.点评:此题属于图形的切拼问题,考查学生的空间想象力,通过画图,解决问题.22.由以上分析,拼法如下:【解析】试题分析:根据题意,要求用的纸片最少,应尽量用边长最大的,但通过操作,如果用边长4的,但用的边长1的会更多.因此应用:一张边长为3的,三张边长为2的,四张边长为的,这样用的张数最少.解:由以上分析,拼法如下:共用了8张纸片.一张边长为3的,三张边长为2的,四张边长为1的,共用了8张纸片.点评:此题既要抓住拼成的正方形边长为5,还要考虑“最少〞.23.如下图:文案大全【解析】试题分析:通过观察,图中一共32个小正方形,平均分成四个局部,每个局部就要有8个小正方形,根据要求,作出图形即可.解:如下图:点评:此题考查了学生想象、思维以及实际操作能力.24.如下图:【解析】试题分析:因为长方形面积为25×16=400〔平方厘米〕,拼成的正方形的面积也应是400平方厘米,因此正方形的边长应为20厘米,如下列图所示.解:如下图:点评:根据长方形和正方形面积相等进行剪拼.25.由以上分析,图示如下:【解析】文案大全实用标准文档试题分析:把长方形纸片右边2列5行剪去,再把剪下的局部2列2行〔即a〕,补在右下角〔即a〕;然后再在剪下的剩余局部中剪掉b和c,补在如下图图2的b和c局部;最后把剩下的d和c剪开,补在图二d和c局部即可.解:由以上分析,图示如下:点评:此题属于实际操作题,运用实物实际操作一下,问题不难解决.26.①是1个正方形;②4个;③2个;④3个;⑤5个;⑥6个;⑦4个.【解析】试题分析:大正方形中共有25个小正方形,要求分割成七个形状不同的长方形〔包含正方形〕,那么先从分成的正方形的个数入手:1+2+3+4+5+6=21,还剩4个,拼成一个正方形即可.解:①是1个正方形;②4个;③2个;④3个;⑤5个;⑥6个;⑦4个.点评:此题考查学生综合分析以及进行实际操作的能力.27.由分析可知,答案如图,【解析】试题分析:首先沿着其中两个方格的对角线分割成两局部:;文案大全实用标准文档拼成如图:再沿图分割:对应把①②放到④③的位置即可.解:由分析可知,答案如图,点评:此题主要考查图形的分割与拼凑,注意第一次分割拼凑后第二次分割.28.由分析可得:效果图:文案大全实用标准文档【解析】试题分析:由题意,一个大长方形左上角缺少一个2×3的小长方形,那么这个图形的面积是7×5﹣2×3=29,把这个图形分成三局部,再拼成一个正方形,那么正方形的面积就是29,因为5×5=25,可知正方形的边长大于5,由于29=25+4,所以可想法剪下两个直角边为5、2的直角三角形来拼组,其斜边就是正方形的边长;据此解答即可.解:由分析可得:效果图:点评:解答此题关键是明确正方形的面积是29,29=25+4,进而得出剪切小直角三角形拼组.29.〔1〕要形成2种面积不同的小正方形,假设大正方形面积为6×6,那么分成8个2×2,4个1×1;〔2〕要形成3种面积不同的小正方形,假设大正方形面积为6×6,那么分成1个4×4,3个2×2,8个1×1;文案大全实用标准文档〔3〕要形成4种面积不同的小正方形,假设大正方形面积为7×7,那么分成1个4×4,2个3×3,2个2×2,7个1×1.【解析】试题分析:根据分成正方形面积的三种情况,假设大正方形面积为6×6或7×7,很容易解决问题.解:〔1〕要形成2种面积不同的小正方形,假设大正方形面积为6×6,那么分成8个2×2,4个1×1;〔2〕要形成3种面积不同的小正方形,假设大正方形面积为6×6,那么分成1个4×4,3个2×2,8个1×1;〔3〕要形成4种面积不同的小正方形,假设大正方形面积为7×7,那么分成1个4×4,2个3×3,2个2×2,7个1×1.点评:此题考查了学生实际操作以及空间想象力,此题有多种答案.30.由以上分析可得:文案大全实用标准文档【解析】试题分析:先画出一个三角形,然后找出每边的中点,两两连接这3个中点,就把三角形分割成4个,同理,继续找出四个三角形的中点,连接就可以了.解:由以上分析可得:点评:此题解答的关键在于找出三角形的中点,两两连接这3个中点,进行分割.文案大全。

第十五讲一个图形的等积变换
把一个图形切开后组拼成另一个图,它的形状变了但(面积)大小未变,这样的过程叫做图形的等积变换。
例1 把下面的长方形剪一刀,将它分成两个同样的直角三角形。
然后用这两个直角三角形拼成另外形状的图形。
试试看。
解:
例2 给你一个梯形,先将它折叠两次(如图示),再沿三角形一边的那条折痕剪开,拼成一个三角形。
解:
例3右图由五个小正方形组成,请先用剪刀把它剪开,然后重新拼成一个大正方形。
解:此题有很多种不同的切拼方法,这里只举一种。
把小正方形剪下来,再将剩下的大正方形等分成四个直角三角形,再像下面的右图那样拼成一个大正方形。
习题十五
1.把一个平行四边形折叠展开描痕分成二等分,沿折痕剪开后,再拼成另一个平行四边形。
2.把下图中的长方形纸片先剪成两个大小相同的正方形,再把每个正方形纸片剪成两块,然后拼成一个大正方形。
怎样剪,怎样拼?
3.下图所示这块木料可看成由五个小正方形组成。
聪明的木工只据了两次,就拼出了一个正方形桌面。
想一想,他是怎样锯、怎样拼的?
4.请把下图中的长方形分成形状相同、大小相等的两块,然后再拼成一个正方形。
5.请把下图中的正方形分成形状相同、大小相等的四块,然后再拼成一个等腰直角三角形。
6.把下面的图形剪两刀变成三块,再把这三块拼成一个正方形。
习题十五解答。
图形的剪拼kèqiánhuódòng课前活动míyǔcāi yīzhǒngkūnchóng 谜语( 猜一种昆虫) tiānrèpáshàngshùshāo天热爬上树梢,yǎnjīng 眼睛zǒngàidàhǎndàjiào 总爱大喊大叫。
c hìbǎng 翅膀míngmíngsháyěbùdǒng明明啥也不懂,piānshuōzhīdàozhīdào偏说知道知道。
dáàn zhīliǎo chán答案:知了( 蝉)【例1】(★★)qǐng nǐzhǔnbèi yīzhāngzhèngfāngxíngdezhǐànxiàmiàndeyāoqiújiǎn yī请你准备一张正方形的纸,按下面的要求剪一jiǎn剪。
jiǎnyīdāoshǐxiàmiandezhèngfāngxíngbiànchéngliǎnggèxíngzhuàng⑴剪一刀使下面的正方形变成两个形状,dàxiǎoyíyàngdetúxíng大小一样的图形。
jiǎnliǎngdāoshǐzhèngfāngxíngbiànchéng sìgèxíngzhuàng dàxiǎo yí⑵剪两刀使正方形变成四个形状,大小一yàngdetúxíng样的图形。
zàiyīzhāngzhǐdezhōngjiānjiǎnxiàyīgèyuán⑶在一张纸的中间剪下一个圆。
第十五讲 图形剪拼前续知识点:一年级第一讲;XX 模块第X 讲 后续知识点:X 年级第X 讲;XX 模块第X 讲萱萱 阿瓜萱萱 小高小高阿呆小高阿瓜阿呆这么大的地方,我们四个人种树,怎么分配呀?这个很容易,你们看,这块地是正方形的,我们把它平均分成4块,然后每人负责一块地方就可以了.把相应的人物换成红字标明的人物.在前面的学习中,我们已经认识了很多的图形,如果将我们已经认识的图形拼一拼、剪一剪,它们会变成什么图形呢?看看我们自己能够想到多少种不同的方法.例题1用4个完全相同的小正方形,可以拼成哪些不同的平面图形呢?拼一拼,画一画.【提示】自己动手拼一拼.练习1如图,有4个完全相同的三角形,用它们可以拼成哪些平面图形呢?拼一拼,画一画.例题2把下面的正方形分成形状相同、大小相等的4个图形,可以怎么分?(用虚线表示)【提示】把正方形折一折.练习2把一张形状为“L”的纸,剪成4个形状相同、大小相等的图形.你有几种剪法?(用虚线表示)将认识的图形剪成形状相同、大小相等的图形有多种方法.但在有限制条件的情况下应该如何考虑呢?一起动手试一试.例题3请把下面的正六边形分割成4个形状相同、大小相等的图形,使每个图形中都含有一个小朋友.【提示】要保证小朋友的完整.练习3请把下面的图形分割成4个形状相同、大小相等的图形,使每个图形中都含有一个蘑菇娃娃.例题4请把下面的长方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一只小青蛙.【提示】一共有12个格子,分割成4个形状相同、大小相等的图形,每个图形应该有几个格子呢?练习4请把下面图形分割成4个形状相同、大小相等的图形,使每个图形中都含有一只小老虎.例题5请把下面的正方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一只小猫.【提示】紧挨着的相同的动物一定是要隔开的.例题6请把下面的正方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一只小鸟和一条小鱼.【提示】4个形状相同、大小相等的图形可以是这样的吗?课外阅读四巧板作业1. 如图,有4个完全相同的三角形,用它们可以拼成哪些不同的平面图形呢?在右边的方框中画一画.2.请把下面的长方形剪成形状相同、大小相等的4个图形.(用虚线表示)3. 请把下面的长方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一个★.4. 请把下面的正方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一个☆.5. 把下面的正方形分割成4个形状相同、大小相等的图形,使每个图形中都含有一个☆和一个★.☆☆ ☆★ ☆ ★★★☆☆☆☆★ ★★★第十五讲图形剪拼1.例题1答案:答案不唯一“一”型“L”型“T”型“Z”型“田”型详解:拼的过程中有序思考:一行有4个正方形;一行有3个正方形;一行有2个正方形;一行有1个正方形.2.例题2答案:答案不唯一详解:想把一个图形4等分,可以先对其2等分,再对每一份2等分,就是把原图形4等分.此题答案无穷多种.另外,可以通过找中心点进行分割.(如最后3个图,先找到正方形的中心点,从中心点出发,分割成相同的4个图形,有无穷多种分割方法.)3.例题3答案:详解:这是一个正六边形,先把它一分为二,再对每一份二等分.由于有了包含小朋友的限制,所以在分割时要注意保证小朋友的完整.4.例题4答案:详解:“一”型分割法和“拐角”分割法.5.例题5答案:详解:运用“L”型分割法.6.例题6答案:详解:运用“L”型分割法.7.练习1答案:答案不唯一简答:动手拼一拼.8.练习2答案:……简答:把一个图形4等分,可以先对其2等分,再对每一份2等分,就是把原图形4等分.9.练习3答案:答案不唯一简答:先把它一分为二,再对每一份二等分.10.练习4答案:简答:运用“拐角”分割法.11.作业1答案:答案不唯一简答:通过尝试,可以得到:4个小正三角形可以拼成一个大平行四边形或大三角形等.12.作业2答案:答案不唯一简答:想把一个图形4等分,则先对其2等分.再对每一份2等分,即把原图形4等分.13.作业3答案:答案不唯一简答:可以采用“一”型和“拐角”分割法.14. 作业4答案:答案不唯一 简答:如图所示,划分成4个田字形即可,也有其它划分方法.15. 作业5答案:简答:可以采用“L ”型分割法.☆☆ ☆★ ☆★★ ★ ☆☆☆☆ ★★★ ★ ★ ★ ★★。
一年级数学思维训练:《剪拼图形》所属体系板块:第二级上主要知识点:1)图形的剪分:对折、过中心点折;等分2)图形的拼组:一般先拼大图形3)图形的剪拼:在原图上找目标能力培养:动手能力,空间想象能力体系对接:第三级上图形七十二变预习题目:下面有一张正方形纸,你能把它分成四个形状、大小都一样的图形吗?你能想到几种方法呢?《剪拼图形》知识点一、图形的剪分1、等分:①对折②过中心点折【例】剪一刀使下面的正方形变成两个形状、大小一样的图形.【解析】将图形分成形状、大小一样的图形,这样的分法叫等分.等分,可以通过“对折”、“过中心点折”,折纸帮助我们找到“折痕”,沿着相应折痕剪,就可以将图形等分.剪法如下:2、二等分→四等分→八等分→……对折一次:两等分对折两次:四等分(对折三次:八等分)二、图形的拼组先找大图形,补成目标图形能拼就能分【例】用下面同样大小的两个直角三角形拼成一个平行四边形.【解析】首先要了解直角三角形和目标图形“平行四边形”的特点.拼图形,必须边对边拼,而且是一样长的边才能拼.可以拼出两种平行四边形,如下:三、图形的剪拼找目标(原图上找)【例】把下面形状的纸片剪一刀,再拼成一个正方形.【解析】观察图形,目标是正方形,可以在原图上画出目标正方形,多出的部分剪掉,补到缺的地方,即可得到目标图形.四、七巧板游戏1、认识七巧板的七个图形2、一般先拼大的,再拼特殊的《剪拼图形》课后拓展练习1、小山羊带来一个等边三角形,你能帮忙剪一刀把等边三角形变成两个形状、大小一样的图形吗?2、小蜜蜂找到了下面三种图形,你能拼成一个梯形吗?3、小蜜蜂右边有四个图形中,选哪两个可以拼成一个长方形的图形呢?4、把左边的图形剪一刀,你能拼成右边的图形么?【参考答案】:1、知识点:对折、等分2、知识点:拼图形3、知识点:拼图形,先拼大图形(1)和(3)可以拼成一个长方形.4、知识点:剪拼图形,在原图上找目标将下面的粗黑线剪开,把左边剪下来的拼到右边.。
2019年小学奥数几何专题——图形剪拼1.用一条线段把一个长方形平均分割成两块,一共有多少种不同的分割法?2.把任意一个三角形分成面积相等的4个小三角形,有许多种分法.请你画出4种不同的分法.3.把任意一个三角形分成面积相等的2个小三角形,有许多种分法.请你画出3种不同的分法.4.怎样把一个等边三角形分别分成8块和9块形状、大小都一样的三角形.5.下图是一个直角梯形,请你画一条线段,把它分成两个形状相同并且面积相等的四边形.6.在一块长方形的地里有一正方形的水池(如下图).试画一条直线把除开水池外的这块地平分成两块.7.把下图四等分,要求剪成的每个小图形形状、大小都一样.除了剪正方形外,你还有别的方法吗?8.下图是一个34⨯的方格纸,请用四种不同的方法将它分割成完全相同的两部分,但要保持每个小方格的完整.9.右图是一个44⨯的方格纸,请用六种不同的方法将它分割成完全相同的两部分,但要保持每个小方格的完整.10.下图是一个被挖去了为总面积四分之一小正方形的大正方形,请你将它分成大小形状完全一样的四部分.11.下图是一个被挖去了为总面积四分之一小正方形的大正方形,请你将它分成大小形状完全一样的两部分.如果分三部分呢?12.图中是由三个正三角形组成的梯形.你能把它分割成4个形第1页/共26页状相同、面积相等的梯形吗?13.下图是由五个正方形组成的图形.把它分成形状、大小都相同的四个图形,应怎样分?14.已知左下图是由同样大小的5个正方形组成的.试将图形分割成4块形状、大小都一样的图形.15.把右图剪成形状、大小相等的8个小图形,怎么剪?作出分出的小图形.16.下图是由18个小正方形组成的图形,请你把它分成6个完全相同的图形.17.一个正三角形形状的土地上有四棵大树(如下图所示),现要把这块正三角形的土地分成和它形状相同的四小块,并且要求每块地中都要有一棵大树.应怎样分?18.将下图分割成大小、形状相同的三块,使每一小块中都含有一个○.19.请把下面这个长方形沿方格线剪成形状、大小都相同的4块,使每一块内都含有“奥数读本”这四个字中的一个,该怎么剪?20.请把下面的图形分成形状、大小都相同的4块,使每一块里面都有“春蕾杯赛”4个字.21.学习与思考对小学生的发展是很重要的,学习改变命运,思考成就未来,请你将下图分成形状和大小都相同的四个图形,并且使其中每个图形都含有“学习思考”这四个字.应怎样分?22.如下图所示,请将这个正方形分切成两块,使得两块的形状、大小都相同,并且每一块都含有学而思奥数五个字.23.如下图所示的正方形是由36个小正方格组成的.如图那样放着4颗黑子,4颗白子,现在要把它切割成形状、大小都相同的四块,并使每一块中都有一颗黑子和一颗白子.试问如何切割?24.如图,甲、乙是两个大小一样的正方形.要求把每一个正方形分成四块,两个正方形共分为八块,使每块的大小和形状都相同,而且都带一个○.甲乙25.正三角形ABC的面积是1平方米,将三条边分别向两端各延长一倍,连结六个端点得到一个六边形(如图),求六边形的面积.26.正六边形ABCDEF的面积是1平方米,将六条边分别向两端各延长一倍,交于六个点,组成如下图的图形,求这个图形的面积.27.如图,它是由15个边长为1厘米的小正方形组成的.⑴请在原图中沿正方形的边线,把它划分为5个大小形状完全相同的图形,分割线用笔描粗.⑵分割后每个小图形的周长是厘米.⑶分割后5个小图形的周长总和与原来大图形的周长相差厘米.28.如何把下图中的三个图形分割成两个相同的部分(除了沿正方形的边进行分割外,还可沿正方形的对角线进行分割).29.如图,将一个等边三角形分割成互相不重叠的23个较小的等边三角形(这些较小的等边三角形的大小不一定都相同),请在图中画出分割的结果.30.如图,将一个正方形分割成互相不重叠的21个小正方形,这第3页/共26页些小正方形的大小不一定相同,请画图表示.31.用两块大小一样的等腰直角三角形能拼成几种常见的图形?32.用3个等腰直角三角形拼图,要求边与边完全重合,能拼出几种图形?33.用同样大小的四块等腰直角三角板,能否拼出一个三角形、一个正方形、一个长方形、一个梯形、一个平行四边形五种图形?若能,画出示意图.34.下面哪些图形自身用4次就能拼成一个正方形?35.用下面的3个图形,拼成右边的大正方形.36.用“四连块”拼成一个正方形,按编号画入右边图中.37.有6个完全相同的,你能将它们拼成下面的形状吗?38.三种塑料板的型号如图:已有A型板30块,要购买B、C两种型号板若干,拼成55⨯正方形10个,B型板每块价格5元,C型板每块价格为4元.请你考虑要各买多少块,使所花的总钱数尽可能少,那么购买B、C两种板要花多少元?39.试用图a中的8个相等的直角三角形,拼成图b中的空心正八边形和图c中的空心正八角星.40.试将一个正方形分成相同的四块,然后用这四块分别拼成三角形、平行四边形和梯形.41.把两个小正方形剪开以后拼成一个大正方形.42.将下图分成4个形状、大小都相同的图形,然后拼成一个正方形.43.试将一个49⨯的长方形分割成两个大小相等、形状相同的图形,然后拼成一个正方形.44.长方形的长和宽各是9厘米和4厘米,要把它剪成大小、形状都相同的两块,并使它们拼成一个正方形.45.将下图分成两块,然后拼成一个正方形.46.将图分成4个形状、大小都相同的图形,然后拼成一个正方形.47.小龙的妈妈在街上卖边角布料的地摊上,买回了一块形状是等腰直角三角形的绸布,想用它来做长方形的窗帘,为了不把布剪的太碎,裁剪的块数就要尽可能的少,请问小龙的妈妈应该怎样剪拼呢?48.试将任意一个三角形分成三块,然后拼成一个长方形.49.试将任意一个矩形分成两块,然后拼成一个三角形.50.试将任意一个矩形分成三块,然后拼成一个三角形.51.把一个正方形分成8块,再把它们拼成一个正方形和一个长方形,使这个正方形和长方形的面积相等.52.有一块长8米、宽3米的长方形地毯,现在要把它移到长6米、宽4米的新房间里.请找出一种剪裁方法,使剪后的各块拼合后正好能铺满房间的地面,为了使剪后的地毯尽量完整,就要使剪裁的块数尽可能地少,应怎样剪拼?53.如何把一个长20厘米、宽12厘米的长方形切成两块,拼成一个长16厘米、宽15厘米的新长方形.54.长方形长24厘米,宽15厘米.把它剪成两块,使它们拼成一个长20厘米,宽18厘米的长方形.55.如下图长方形的长、宽分别为120厘米、90厘米,正中央开第5页/共26页有小长方形孔,长为80厘米,宽为10厘米,要拼成面积为100平方厘米的正方形.问如何切分,能使划分的块数最少.56.把下图中两个图形中的某一个分成三块,最后都拼在一起,使它们成为一个正方形.57.如下图两个正方形的边长分别是a和b(a b ),将边长为a的正方形切成四块大小、形状都相同的图形,与另一个正方形拼在一起组成一个正方形.58.如下图所示,这是一张十字形纸片,它是由五个全等正方形组成,试沿一直线将它剪成两片,然后再沿另一直线将其中一片剪成两片,使得最后得到的三片拼成两个并列的正方形.参考答案1.无穷多【解析】怎样把一个图形按照规定的要求分割成若干部分呢?这就是图形的分割问题.按照规定的要求合理分割图形,是很讲究技巧的,多做这种有趣的训练,可以培养学生的创造性思维,发展空间观念,丰富想象,提高观察能力.这道题要求把长方形平均分割成两块,过长方形中心的任意一条直线都可以把长方形平均分割成两块,根据这点给出如下分法(如右图):⑴做长方形的两条对角线,设交点为O⑵过O点任作一条直线AB,直线AB将长方形平均分割成两块.可见用线段平分长方形的分法是无穷多的.2.【解析】根据等底等高的三角形面积相等这一结论,只要把原三角形分成4个等底等高的小三角形,它们的面积必定相等.而要得到这4个等底等高的小三角形,只需把原三角形的某条边四等分,再将各分点与这边相对的顶点连接起来就行了.根据上面的分析,可得如左下图所示的三种分法.又因为4 1 4 22=⨯=⨯,所以,如果我们把每一个小三角形的面积看做1,那么14⨯就可以视为把三角形的面积直接分成4等份,即分成4个面积为1的小三角形;而22⨯可以视为先把原三角形分成两等份,再把每一份分别分成两等份.根据前面的分析,在每次等分时,都要想办法找等底等高的三角形.根据上面的分析,又可以得到如右下图的另两种分法.第1页/共26页3.【解析】根据等底等高的三角形面积相等这一结论,只要把原三角形分成2个等底等高的小三角形,它们的面积必定相等.而要得到这2个等底等高的小三角形,只需找出原三角形的某条边的中点与这边相对的顶点连接起来就行了.4.【解析】⑴分成8块的方法是:先取各边的中点并把它们连接起来,得到4个大小、形状相同的三角形,然后再把每一个三角形分成两部分,得到如左上图所示的图形. ⑵分成9块的方法是:先把每边三等分,然后再把分点彼此连接起来,得到加上右上图所示的符合条件的图形.5.【解析】直角梯形的上底为1,下底为2,要分成两个相同的四边形,需要一条边可以分成1和2,AD 边长正好为3,所以AD 边分成两段,找到AD 的三等分点E ,现在,CD AE =,DE AB =,BF EF =,所以还要找到BC 的中点F ,连接EF ,就把梯形ABCD 分成完全相同的两部分.如右上图.6.【解析】用连对角线的办法找出这块长方形地的中心O 和正方形水池的中心A .过O 、A 画一条直线,这条直线正好能把除开水池外的这块地平分为两块(如右上图).7.【解析】先把图形分成2040⨯相等的两块,每一块中再分成相等的两份,这样就不难分成四块了,如右上图.8.【解析】分成的两块每块有1226÷=(个)小格,并且这两块要关于中心点对称,大小和形状完全一样,我们从对称线入手,介绍一种分割技巧——染色法,先选中一个小格,找它关于中心点或中心线的对称位置,标上相应的符号.当找它关于中心线的对称位置时是一种情况,关于中心点的对称位置是另一种情况。