一年级奥数之有趣的立体图形

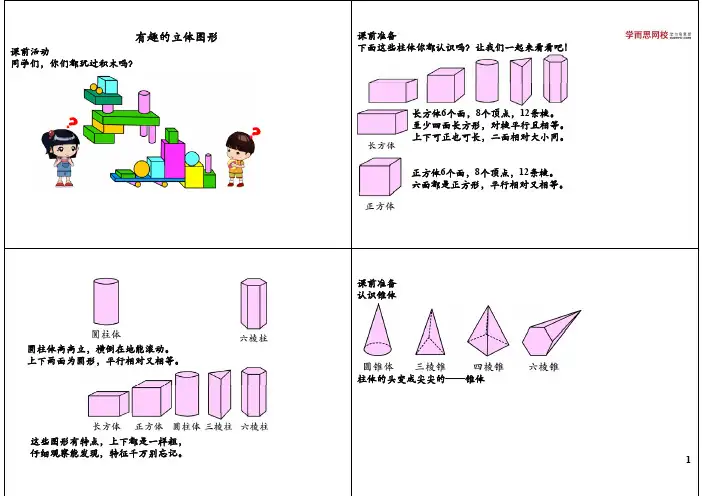
课前活动课同学们，你们都玩过积木吗？课前准备下面这些柱体你都认识吗？让我们一起来看看吧！长方体个面个顶点条棱6个面，8个顶点，12条棱。

至少四面长方形，对棱平行且相等。

上下可正也可长二面相对大小同上下可正也可长，二面相对大小同。

正方体6个面，8个顶点，12条棱。

六面都是正方形，平行相对又相等。

圆柱体高高立，横倒在地能滚动。

上下两面为圆形平行相对又相等上下两面为圆形，平行相对又相等。

这些图形有特点上下都是样粗这些图形有特点，上下都是一样粗，课前准备认识锥体柱体的头变成尖尖的——锥体课前准备认识球体将实物与中间对应的图形连接起来。

“我是球，我圆圆的脑袋，圆圆的脸，我站不稳，我跑得快。

篮球排球都是我，娱乐健身好伙伴！”小提示：球是可以滚动的立体的球是球体的简称球是可以滚动的，立体的，球是球体的简称。

圆是不能滚动的，平面的，可以用球体来画出圆。

【拓展】(★★)左边的两堆方块拼起来，是右边的哪一堆？用线连起来。

【例2】(★★★)找不同，把下图中不同于其它类的立体图形圈起来。

上面的这些图形可以拼成下面的哪种立体图形呢？连一连。

从下面的立体图形中能找到哪些平面图形？请你连一连。

大圆变小圆在一张纸上画了一个大圆，聪明的小朋友们，你能够将这张纸折叠，使大圆变成一个小圆吗？快来试一试吧！乐乐老师答疑互动群【铺垫】(★★)我会数方块同学们，你知道下图一共有多少个方块吗？【例5】(★★★★)下图由正方体堆成，数一数共有多少个正方体？【拓展】(★★★★)数一数，下图的图形各用几个方块堆成的？【例6】(★★★★★)下面的塔是由几块小方块堆成的？【拓展】(★★★★)数一数，下图的图形各用几个方块堆成的？二、(常见)的立体图形三、立体图形与平面图形的转换①立体图形→→平面图形①图拆平图。

数立体图形善智知识点：认真思考，结果要用算式表达出来•数图形，按顺序，先数小，再数大立体的，有隐藏，分层数，再相加课堂共同练习：1. 下图有（）个正方形?2. 下图有（）个长方形?5. 数一数下面的图形各由几个小正方体组成，并画出从它们的正面看到的形状.6. 用正方体摆成下图，数一数一共有几个小正方体，其中几个能看见，几个看不见?一共（）个看见（）个看不见（）个一共（）个看见（）个看不见（）个LW一共（）个看见（）个看不见（）个7. 数一数下面每个立体图形各有几个小正方体.4.数图形:(［个）牛8. 数一数，下面的立体图形是由几个小正方体搭成的?10.数一数下面物体中各有几个小正方体.12.数一数，下图中一共有（ ）个正方体A.6个B.7 个C.8 个9.给下列图形，再添加（）个小正方体，就能组成一个大正方体( )个11.数一数下面物体中各有几个小正方体.（ ）个 （ ）个课后自我提升:1. 数一数下图分别有几个图形？田m()个正方形()个长方形2. 数一数，下图有几个三角形?(1) ________________________ 按层数：下面一层有 __________ 个正方体，中间一层有 _________ 个正方体，上面一层有_______________________ 个正方体.(2) ________________________ 按前后排数：前排有 ____ 个正方体，后排有个正方体.(3) _____________ —共有个正方体.5.数一数下列物体是由几个小正方体拼成的( )个( )个( )个6.数一数下面物体中各有几个小正方体.()个7.数一数下面物体中各有几个小正方体.( )个( )个参考答案：课堂共同练习：5 6 10 5 、4、7 5 、8、7 6 13、10、10 3 个8 、10 20 、30课后自我提升题略5 、9、8 C。

立体几何图形是数学中一个重要的组成部分。

这节课通过看一看、认一认、想一想等活动使大家认识最基础的立体几何图形，从而增加对图形的感性认识，培养初步的图形概念认识，为以后的学习打下良好的基础。

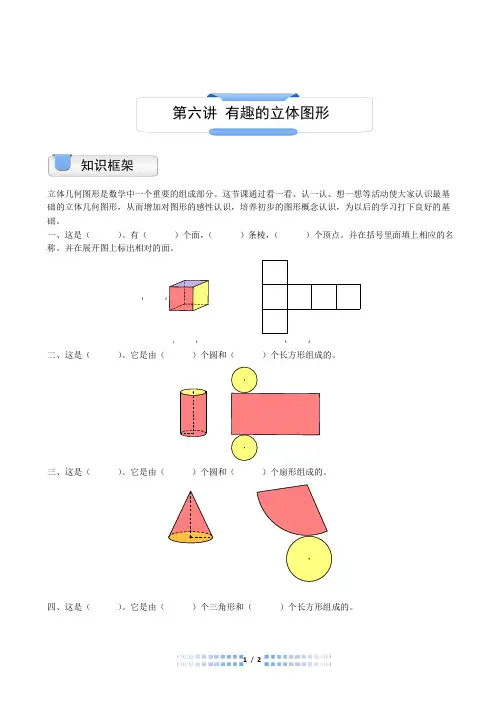
一、这是（ ）。

有（ ）个面，（ ）条棱，（ ）个顶点。

并在括号里面填上相应的名称。

并在展开图上标出相对的面。

二、这是（ ）。

它是由（ ）个圆和（ ）个长方形组成的。

三、这是（ ）。

它是由（ ）个圆和（ ）个扇形组成的。

四、这是（ ）。

它是由（ ）个三角形和（ ）个长方形组成的。

( )
( )( )知识框架
第六讲 有趣的立体图形
五、将下图中(1)、(2)号棱锥剪开铺平后，哪一个是它对应的展开图，请用线连起来。

六、下图有哪些图形组成？
七、请你将能找到的包装盒如：月饼盒、冷饮盒、鞋盒等等，用剪刀剪开，平铺在桌面上观察并画出展开图。

立体几何图形是数学中一个重要的组成部分。

这节课通过看一看、认一认、想一想等活动使大家认识最基础的立体几何图形，从而增加对图形的感性认识，培养初步的图形概念认识，为以后的学习打下良好的基础。

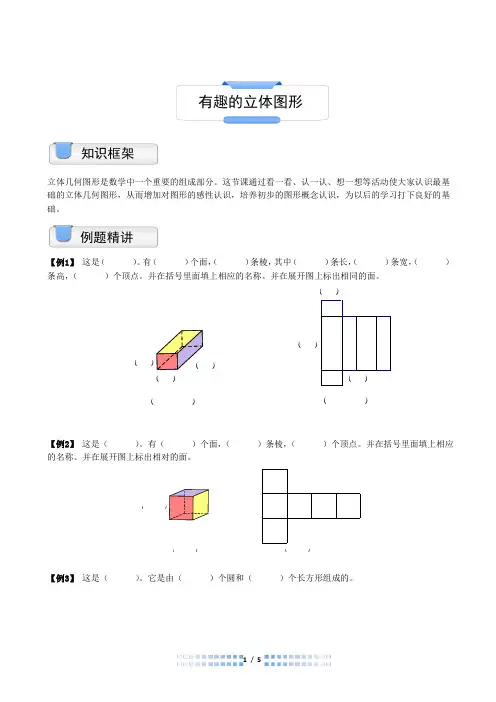
【例1】 这是（ ）。

有（ ）个面，（ ）条棱，其中（ ）条长，（ ）条宽，（ ）条高，（ ）个顶点。

并在括号里面填上相应的名称。

并在展开图上标出相同的面。

【例2】 这是（ ）。

有（ ）个面，（ ）条棱，（ ）个顶点。

并在括号里面填上相应的名称。

并在展开图上标出相对的面。

【例3】 这是（ ）。

它是由（ ）个圆和（ ）个长方形组成的。

( )( )( )( )( )( )( )( )( )( )( )例题精讲知识框架有趣的立体图形【例4】这是（）。

它是由（）个圆和（）个扇形组成的。

【例5】这是（）。

它是由（）个三角形和（）个长方形组成的。

【例6】这些是（）。

【例7】这是（）。

【例8】 这是（ ）。

【随练1】 认一认，请在下面的括号里填上正确的名称。

【随练2】 将下图中(1)、(2)号棱锥剪开铺平后，哪一个是它对应的展开图，请用线连起来。

( )( )( )( )( )( )( )( )( )( )( )( )课堂检测家庭作业【作业1】看看摸摸，并在自己周围寻找具有这些形状的物体。

1．长方体2．正方体3．圆柱4．圆锥5．棱锥6．球【作业2】下图有哪些图形组成？【作业3】下列图中的（1）（2）（3）号盒子剪开铺平后，展开图是哪一个，请你用线连起来。

【作业4】用一些立体图形画一幅画吧！【作业5】请你将能找到的包装盒如：月饼盒、冷饮盒、鞋盒等等，用剪刀剪开，平铺在桌面上观察并画出展开图。

第十一讲立体图形计数前续知识点：一年级第一讲；XX模块第X讲后续知识点：X年级第X讲；XX模块第X讲墨莫墨莫卡莉娅小高把相应的人物换成红字标明的人物．还记得我们都学习过哪些立体图形吗？正方体、长方体、圆柱体、球体……数不胜数．今天我们来学习一下立体图形的计数．在地球上，一个小正方体可以在没有任何支撑的情况下悬浮在空中吗？答案当然是不可以！聪明的你赶快来看一看，下面题目中的立体图形到底由几个小正方体组成的呢？例题1数一数，它们分别由几个小正方体组成？【提示】有没有看不见的正方体？练习1数一数，它们分别由几个小正方体组成？数正方体有许多方法，其中我们可以一层一层的分层数，试试看．例题2左边方框中的立体图形和右边哪个立体图形中的小正方体个数相同呢？【提示】数一数，分别有几个小正方体！练习2左边方框中的立体图形和右边哪个立体图形中的小正方体个数相同呢？分层数的方法不仅简单快捷，而且清晰明了，不容易数重数漏．结合找规律的方法，我们更能轻松数出立体图形的个数．例题3数一数，下面这个“宝塔”由多少个小正方体组成？A BC DA B【提示】找一找，每层之间有什么规律？练习3数一数，下面这个“楼梯”由多少个小正方体组成？例题4要想把下面左边的立体图形补全成为一个完整的大正方体，至少需要再加几个小正方体呢？【提示】左边的立体图形由几个小正方体组成的？右边的呢？练习4要想把下面左边的立体图形补全成为一个完整的大正方体，至少需要再加几个小正方体呢？例题5要想把下面的立体图形补全成为一个完整的大正方体，至少需要再加几个小正方体呢？【提示】补全后的大正方体是什么样的呢？例题6如图所示，将大正方体中的“L”形挖穿，你能数出现在这个立体图形有多少个小正方体吗？【提示】挖穿了几层？课外阅读长方体和正方体的故事长方体是一个聪明的小男孩儿，他生活在一个数学图形的古老部落．长老们说他们一直拥有自然女神的庇护，自然女神总是不定期地出现在他们部落，每一次，她都只见一个有缘人，如果这个有缘人能够通过她的考验，她就会满足这个有缘人的一个合理的愿望．有一天，长方体去小河边玩，已经有一些伙伴在河边嬉戏，有三角形，正方形，圆等等……长方体刚走到附近就听到三角形喊救命，原来是平行四边形掉到河里去，长方体奋不顾身地跳进了河里，拼死救人．最后长方体把平行四边形救出来了．大家都很感谢长方体．长方体坐在草原上看风景，自然女神出现了．自然女神说：“你已经通过了我的考验，告诉我，你有什么愿望？”长方体说：“我没有什么愿望．”自然女神说：“既然你不说，那我就自作主张替你做决定了．”自然女神知道长方体一个人玩，没有伙伴，就创造了正方体，正方体和长方体一样聪明，而且，正方体和长方体还十分相似，有许多共同的特点．长方体很喜欢这个新伙伴．长方体对自然女神说；“我很喜欢正方体，他有许多和我相似的地方，像我的影子，但又和我完全不一样，有自己的个性．”自然女神说：“你喜欢就好，其实，正方体是另一个特殊的你．比你自己还要特别的你．以后，你自然会明白的．”作业1. 数一数，它们分别由几个小正方体组成？2. 左边方框中的立体图形和右边哪个立体图形中的小正方体个数相同呢？3. 数一数，下面这个“楼梯”由多少个小正方体组成？C B4. 要想把下面左边的立体图形补全成为一个完整的大正方体，至少需要再加几个小正方体呢？5. 如图所示，将大正方体中的“T”字形挖穿，现在这个图形中有几个小正方体？第十一讲 立体图形计数1. 例题1答案：5；5；9；10详解：先数出能看到的正方体个数，再数出看不见的正方体个数，相加即可．2. 例题2答案：A详解：左边方框中的立体图形的小正方体个数为10个，A 的小正方体个数为10个，B 的小正方体个数为9个，C 的小正方体个数为8个，D 的小正方体的个数为11个．3. 例题3答案：35详解：每层的小正方体个数分别为1、3、6、10、15，加起来的和为35．规律是每层分别在上一层的基础上增加2、3、4、5个小正方体．4. 例题4答案：2；17详解：第一个图中完整的大正方体中的小正方体个数为8个，左边立体图形中的小正方体个数为6个，还需要862-=（个）．第二个图中完整的大正方体中的小正方体个数为27个，左边立体图形中的小正方体个数为10个，还需要271017-=（个）．5. 例题5答案：48详解：符合要求的完整的大正方体至少需要64个小正方体组成，现在有16个小正方体，还需要再加小正方体641648-=（个）． 6. 例题6答案：52详解：完整的大正方体一共有1616161664+++=个)小正方体，“镂空”部分有333312+++= (个)小正方体，所以还剩下641252-= (个)小正方体．7. 练习1答案：5；4；6；8简答：第三个中有1个看不见的正方体，第四个中有3个看不见的正方体．8. 练习2答案：D简答：左边方框中的立体图形的小正方体的个数为7个，D 的小正方体的个数也为7个．9. 练习3答案：60简答：每层小正方体的个数分别为4、8、12、16、20，加起来的和为60．10. 练习4答案：3；13简答：第一个图中完整的大正方体中的小正方体个数为8个，左边立体图形中的小正方体个数为5个，还需要853-=（个）．第二个图中完整的大正方体中的小正方体个数为27个，左边立体图形中的小正方体个数为4个，还需要271413-=（个）．11. 作业1答案：6；8；9；10简答：观察这两层小正方体，分别数出每一层小正方体的个数，注意“看不见”的小正方体．也可分别数出每列的小正方体个数，加在一起即可．12. 作业2答案：A简答：左边方框中小正方体的个数是10个，而右边各立体图形的小正方体个数分别为：A .10个；B .13个；C .9个；D .9个．13. 作业3答案：20简答：从顶层开始数，最顶层为2个，第二层为4个，第三层为6个，第四层为8个，所以小正方体的个数为246820+++=（个）．14. 作业4答案：9简答：左边的立体图形中小正方体的个数为36918++=（个），完整的大正方体中小正方体的个数为99927++=（个）．还需要小正方体27189-=（个）．15. 作业5答案：44简答：方法一：整个大正方体中小正方体的个数为1616161664+++=（个），“T ”字形中小正方体的个数为555520+++=（个）或4444420++++=（个），所以现在有小正方体642044-=（个）． 方法二：每层剩下的小正方体有11个，共有4层，所以现在有小正方体：1111111144+++=（个）．。

第十二讲 立体图形展开前续知识点：一年级第一讲；XX 模块第X 讲 后续知识点：X 年级第X 讲；XX 模块第X 讲阿呆阿呆卡莉娅 阿呆 卡莉娅阿呆 卡莉娅把相应的人物换成红字标明的人物．把相应的人物换成红字标明的人物．上一讲我们学习了立体图形计数，今天我们来学习一下正方体的展开图．首先来了解下什么是展开图吧．么是展开图吧．例题1桌上的物体有几个面？【提示】别忘了挨在桌子上的面哦！练习1动动手，沿着红粗线剪开小盒子，它有几个面？动动手，沿着红粗线剪开小盒子，它有几个面？例题2沿蓝色粗线剪开画在黑板上的立体图形，得到的平面展开图会是哪个呢？【提示】动手剪一剪！练习2动手试一试，下面哪个图形是左图沿橙黄色粗线剪开的平面图？BA我们学会了立体图形的展开图，下面这些图形有的能折成正方体的小盒子，而有的不能折成正方体的小盒子，你能找出这些“小特务”吗？成正方体的小盒子，你能找出这些“小特务”吗？例题3下面哪个图形能折成正方体的小盒子？为什么？【提示】折一折！想一想！练习3在能折成正方体小盒子的图形下面画“√”．A B CFE D A B C D“一条线，不过4；凹田7，应舍弃．”这句话概括了不能折成正方体小盒子的大部分情况，大家记住了吗？大家记住了吗？我们继续来看看展开图中相对的面有什么特点吧．我们继续来看看展开图中相对的面有什么特点吧．例题4沿虚线折起来，把折成正方体后相对的两个面用相同的符号表示．【提示】折一折！你能发现折成正方体后，对着的面有什么特点吗？练习4找对面游戏：折成正方体后，把相对的两个面用相同的符号表示．找对面游戏：折成正方体后，把相对的两个面用相同的符号表示．（ ） （ ） （ ） （ ）例题5骰子相对两个面的点子数和都为7，根据左边的正方体骰子，在右边的空白部分画出适当的点子图．【提示】找到相对面！例题6【提示】图案的方向要分清哦！课外阅读正方体的平面展开图你知道正方体的平面展开图有多少种吗？你能准确的记忆它们吗？一起来看看这个小窍门吧！下面的正方体中， 的对面是 ， 的对面是 ， 的对面是 ．根据左边的正方体，在右边的空白部分画出适当的图形．作业作业1. 将下图中的（1）、（2）号罐子分别剪开铺平后，哪一个是它们分别对应的展开图，请用线连起来．）号罐子分别剪开铺平后，哪一个是它们分别对应的展开图，请用线连起来．（1） （2）A B第一类，1，4，1型，共六种．记忆方法：中间四个面，上下各一面第二类，2，3，1型，共三种．记忆方法：中间三个面，一、二隔河见第三类，2，2，2型，只有一种． 记忆方法：中间两个面，楼梯天天见记忆方法：中间两个面，楼梯天天见第四类，3，3型，只有一种．记忆方法：中间没有面，三三连一线记忆方法：中间没有面，三三连一线2. 沿粗实线和粗虚线剪开左边的正方体，所得到的平面展开图是（沿粗实线和粗虚线剪开左边的正方体，所得到的平面展开图是（ ）．3. 在不能折成正方体小盒子的图形下面画“×”．4. 折一折．把下图相对的面用相同的符号表示．折一折．把下图相对的面用相同的符号表示．5. 骰子相对的两个面的点子数和都为7，根据左边的正方体骰子，在右边的空白部分画出适当的点子图．（ ）） （ ））（ ））（））AB第十二讲 立体图形展开1. 例题1答案：6个面个面详解：一共有上、下、左、右、前、后6个面．个面． 2. 例题2答案：B详解：找一个基准面，这个基准面就是以原正方体中实线最多的面为准，然后在各个面标上序号，基准面不动，其他面沿着虚线一一展开，观察展开的其他面与基准面的位置关系． 3. 例题3答案：C详解：含有“凹、田、7”或者一条线上的正方形为5个的图形不能折成正方体．A 中含有“凹”，B 中含有“田”，D 中一条线为5，E 中含有“7”，F 中含有“凹”． 4. 例题4答案：答案：详解：“目”“Z ”两端是相对面，找到相对面即可．”两端是相对面，找到相对面即可． 5. 例题5答案：答案：详解：详解：先将图中已有的骰子点数补全，先将图中已有的骰子点数补全，先将图中已有的骰子点数补全，找到对面，找到对面，找到对面，根据骰子相对面的点子数和为根据骰子相对面的点子数和为7的规律，的规律，补全相对面的点子图．补全相对面的点子图．补全相对面的点子图． 6. 例题6答案：答案：详解：首先根据左边正方体上面的图案判断出的位置，然后找到相对面即可．的位置，然后找到相对面即可．7. 练习1答案：6简答：一共有上、下、左、右、前、后6个面．个面．8. 练习2 答案：B简答：沿着蓝色粗线剪开试一试．简答：沿着蓝色粗线剪开试一试．9. 练习3答案：答案：简答：第一个、第三个和第四个都含有“田”，第二个可以折成正方体．，第二个可以折成正方体．10. 练习4答案：答案：简答：找到相对面即可．简答：找到相对面即可．11. 作业1答案：答案：简答：观察立体图形的特征，找到相应的立体图形展开图．12. 作业2答案：A简答：动手剪一剪，可发现剪出来的展开图应为A ．13. 作业3答案：答案： （1） （2）A B (√)简答：一条线，不过四，凹田7，应舍弃．第2个图形中包含“田”，所以不可以折成正方体小盒子．，所以不可以折成正方体小盒子．14. 作业4答案：答案：简答：先判断“目”字形的两个相间的面是对面，剩下的面即为对面．15. 作业5答案：答案：简答：根据左边的正方体骰子可以判断··的·上面，骰子两个相对面的点子数和都为7，再根据找对面的方法判断出每个相对面上的点子数．断出每个相对面上的点子数．（×）（×）。

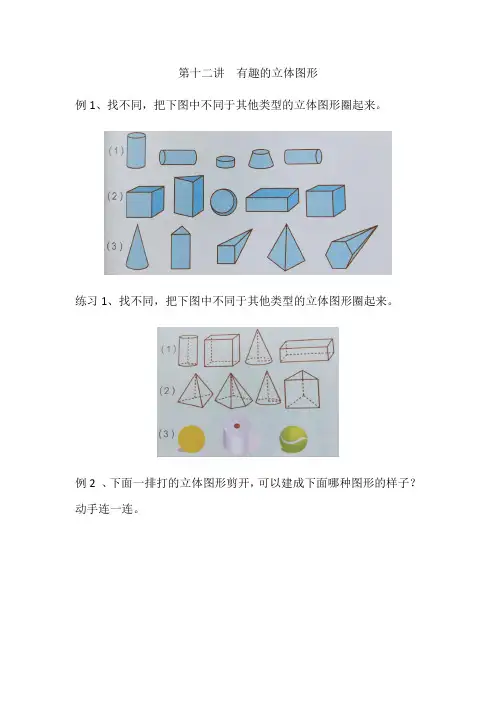
第十二讲有趣的立体图形
例1、找不同，把下图中不同于其他类型的立体图形圈起来。

练习1、找不同，把下图中不同于其他类型的立体图形圈起来。

例2 、下面一排打的立体图形剪开，可以建成下面哪种图形的样子？动手连一连。

练习2、你知道下面的展开图是哪些图形的吗？让我们来连一连吧。

例3、你知道下面的立体图形各有多少个面吗？请把答案填在括号里
练习3、你知道下面的锥体们各有几个面吗？
例4、下面的图形可以折成一个正方体和长方体吗？根据折成的图形判断各面上的字母跟哪个字母是相对的？
（1） （2）
（ ）和（ ）相对
（ ）和（ ）相对 （ ）和（ ）相对 （ ）和（ ）相对
（ ）和（ ）相对 （ ）和（ ）相对
例5、一个正方体剪开可以得到多种不同形状的展开图，下面三个都可以折成正方体吗？可以的画“√”，错误的画“×”。

（
） （ ） （ ） 练习5、下面的展开图都可以折成正方体吗？可以的画“√”，错误
的画“×”。

（）（）（）
例6、判断题你会做吗？正确的画“V”，错误的画“ X ”。

（1）正方体的六个面一定都是正方形。

( )
（2）圆柱和圆柱体的是不同的立体图形。

( )
（3）圆和球是不同的图形。

( )
练习6、判断题：
（1）长方体的六个面一定都是长方形。

（）
（2）球和球体是不同的立体图形。

（）
（3）正方形和正方体是一样的图形。

（）。