八年级上册数学《三角形》单元综合检测(含答案)

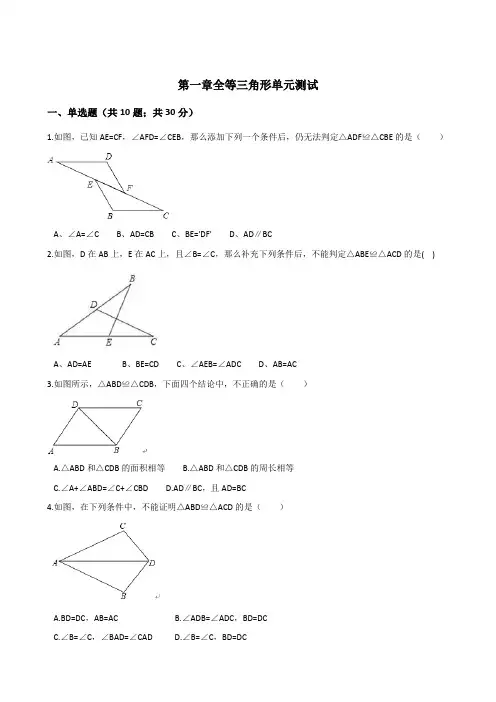
第一章全等三角形单元测试

一、单选题（共10题；共30分）

1.如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（ ）

A、∠A=∠C B、AD=CB C、BE='DF' D、AD∥BC

2.如图，D在AB上，E在AC上，且∠B=∠C，那么补充下列条件后，不能判定△ABE≌△ACD的是( )

A、AD=AE B、BE=CD C、∠AEB=∠ADC D、AB=AC

3.如图所示，△ABD≌△CDB，下面四个结论中，不正确的是（ ）

A.△ABD和△CDB的面积相等 B.△ABD和△CDB的周长相等

C.∠A+∠ABD=∠C+∠CBD D.AD∥BC，且AD=BC

4.如图，在下列条件中，不能证明△ABD≌△ACD的是（ ）

A.BD=DC，AB=AC B.∠ADB=∠ADC，BD=DC

C.∠B=∠C，∠BAD=∠CAD D.∠B=∠C，BD=DC 5.已知图中的两个三角形全等，则∠1等于（ ）

A.72° B.60° C.50° D.58°

6.两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积=12AC•BD，其中正确的结论有（ ）

A.0个 B.1个 C.2个 D.3个

7.如图，已知△ABE≌△ACD，∠1=∠2，∠B=∠C，不正确的等式是（ ）

A.AB=AC B.∠BAE=∠CAD C.BE=DC D.AD=DE

8.如图，已知MB=ND，∠MBA=∠NDC，下列条件中不能判定△ABM≌△CDN的是（ ）

A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN

第7、8单元综合能力检测

(时间：90分钟，满分：100分)

题号 一 二 三 四 总分

得分

一、我会填。(每空2分，共40分)

1．一只平底锅上一次只能同时煎两个蛋，用它煎一个鸡蛋需要2分钟(正、反面各1分钟)，煎3个鸡蛋至少需要( )分钟，煎9个鸡蛋至少需要( )分钟。

2．如图，小明早上起床后要做下面的几件事情。要使所用的时间最少，最少需要( )分钟。

3．条形统计图是用一个格表示一定的( )，根据数量的( )，画成长短不同的( )。因它们是由一个个直条组成的，所以叫条形统计图。

4．如图是星星制药厂2016年前半年的产量统计图，请看图填空。

这半年中，( )月份产量最高，产量是( )吨；( )月份产量最低，产量是( )吨。

5．四(1)班和四(2)班进行乒乓球比赛。每班选出打乒乓球最好的五名同学

(下表中按五名同学的水平高低编号，1号水平最高，5号水平最低)，共打5场球，5局3胜制。假如你是四(1)班同学，你将如何设计，才有可能打赢这次比赛？(把想法填入表中)

第一场 第二场 第三场 第四场 第五场

四(2)班战略 1 2 3 4 5

四(1)班战略

结果

二、我会看。(共18分)

1．(10分)五名学生进行投篮比赛，编号依次是1号、2号、……、5号，每人投20次，投中篮的个数如下图所示。

(1)根据统计图，填写下表：

编号 1号 2号 3号 4号 5号

投中个数(个)

(2)( )号投中最多，( )号投中最少，两人相差( )个。

(3)平均每人投中( )个。

(4)投中个数比平均数少的学生编号是( )。

2．(8分)请根据四年级同学数学考试成绩统计表完成条形统计图。

分数段 100分 80～99分 60～79分 60分以下

人数(人) 6 16 8 10

三、我会合理安排。(每小题6分，共18分)

人教版数学八年级上册

第11章三角形单元检测（A）

（满分：120分时间：120分钟）

一、精心选一选（共2小题，每小题3分，共36分）

1．请根据凸多边形的定义，判断下列选项中不是凸多边形的是（）

2．小华在计算四个多边形的内角和时，得到下列四个答案，则他计算不对的是

（）

A．0

720B．0

1080C．0

1440D．0

1900

3．随着一个多边形的边数增加，它的外角和（）

A．随着增加B．随着减少

C．保持不变D．无法确定

4．过多边形的一个顶点的所有对角线把这个多边形分成6个三角形，则这个多

边形的内角和等于（）

A．0

720B．0

900C．0

1080D．0

1260

5．若四边形ABCD中，∠A：∠B：∠C：∠D=1：2：4：5，则∠A+∠D等于

（）

A．0

30B．0

75C．0

180D．0

210

6．能进行镶嵌的正多边形组合是（）

A．正三角形和正八边形B．正五边形和正十边形

C．正方形和正八边形D．正六边形和正八边形

7．如图，∠1，∠2，∠3，∠4是五边形ABCDE的外角，且∠1=∠2=∠3=∠4=0

70，

则∠AED的度数是（）

A．0

110B．0

108C．0

105D．0

100A B C D

8．能构成如图所示的图案的基本图形是（）

9．若一个多边形的每个外角都是锐角，那么这个多边形的边数至少是（）

A．3 B．4 C．5 D．6

10．鹿鸣社区里有一个五边形的小公园（如图所示），

王老师每天晚饭后都要到公园里去散步，已知图中的

∠1=0

95，王老师沿公园边由A点经B→C→D→Ｅ一

直到F时，他在行程中共转过了（）

A．0

265B．0

275

C．0

360D．0

445

11．一个多边形的每一个内角都是0

144，则它的内角和等于（）

A．0

1260B．0

1440C．0

1620D．0

1800

12．四边形ABCD中，∠A+∠C=∠B+∠D，∠A的一个外角为0

105，则∠C的

度数为（）

A．0

75B．0

90C．0

105D．0

120

二、填空题（共10小题，每小题3分，共30分）

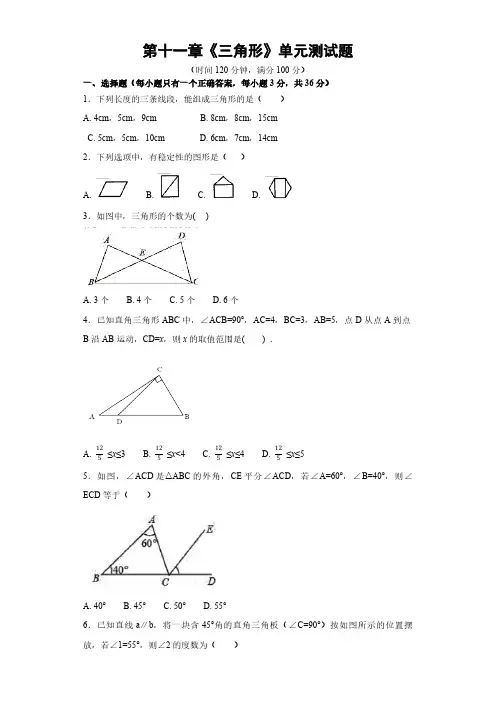
第十一章《三角形》单元测试题

（时间120分钟，满分100分）一、选择题（每小题只有一个正确答案，每小题3分，共36分）1．下列长度的三条线段，能组成三角形的是（ ）

A. 4cm，5cm，9cm B. 8cm，8cm，15cm

C. 5cm，5cm，10cm D. 6cm，7cm，14cm

2．下列选项中，有稳定性的图形是（ ）A. B. C. D.

3．如图中，三角形的个数为( )

A. 3个 B. 4个 C. 5个 D. 6个

4．已知直角三角形ABC中，∠ACB=90°，AC=4，BC=3，AB=5，点D从点A到点

B沿AB运动，CD=x，则x的取值范围是( ) ．

A. ≤x≤3 B. ≤x<4 C. ≤x≤4 D. ≤x≤51251251251255．如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A=60°，∠B=40°，则∠

ECD等于（ ）

A. 40° B. 45° C. 50° D. 55°

6．已知直线a∥b，将一块含45°角的直角三角板（∠C=90°）按如图所示的位置摆

放，若∠1=55°，则∠2的度数为（ ）

A. 80° B. 70° C. 85° D. 75°

7．如图所示，直线a∥b，∠1=35°，∠2=90°，则∠3的度数为（ ）

A. 125° B. 135° C. 145° D. 155°

8．如果一个多边形的内角和是外角和的3倍，则这个多边形的边数是（ ）

A. 8 B. 9 C. 10 D. 11

9．三角形的重心是三角形的（ ）

A. 三条中线的交点 B. 三条角平分线的交点

C. 三边垂直平分线的交点 D. 三条高所在直线的交点

10．如图，已知在△ABC中，AD是高，若∠DAC=50°，则∠C的度数为（ ）

A. 60° B. 50° C. 40° D. 30°

11．已知实数x，y满足，则以x，y的值为两边长的等腰三角形7160xy

的周长是（ ）

A. 30或39 B. 30

八年级数学《全等三角形》单元试卷

考试时间100分钟 满分100分

一、选择题（每题3分共30分）

1、如图1，已知∠A=∠D，∠1=∠2，那么要得到△ABC≌△DEF，还应给出的条件是（ ）

A、∠E=∠B B、ED=BC C、AB=EF D、AF=CD

2、如图2在△ABC中，D、E分别是边AC、BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数为（ ）

A、15° B、20° C、25° D、30°

3、如图3所示，在△ABC中，∠B=∠C，AD为△ABC的中线，那么下列结论错误的是（ ）

A、△ABD≌△ACD B、AB=A

C、AD是△ACD的高 D、△ABC是等边三角形

图1 图2 图3

4、如图4，已知△ABC的六个元素，则下面甲、乙、丙三个三角形中和△ABC全等的图形是（ ）

A、甲和乙 B、乙和丙 C、只有乙 D、只有丙

图4

5、如图5，AO=BO，CO=DO，AD与BC交于E，则图中全等三角形的对数为（ ）

A、2对 B、3对 C、4对 D、5对 6、如图6，已知∠1=∠2，欲证△ABD≌△ACD，还必须从下列选项中补选一个，则错误的选项是（ ）

A、∠ADB=∠ADC B、∠B=∠C C、BD=CD D、AB=AC

图5 图6

7、下列说法正确的有（ ）

①角平分线上任意一点到角两边的距离相等

②到一个角两边的距离相等的点在这个角的平分线上

③三角形三个角平分线的交点到三个顶点的距离相等

④三角形三条角平分线的交点到三边的距离相等

A、1个 B、2个 C、3个 D、4个

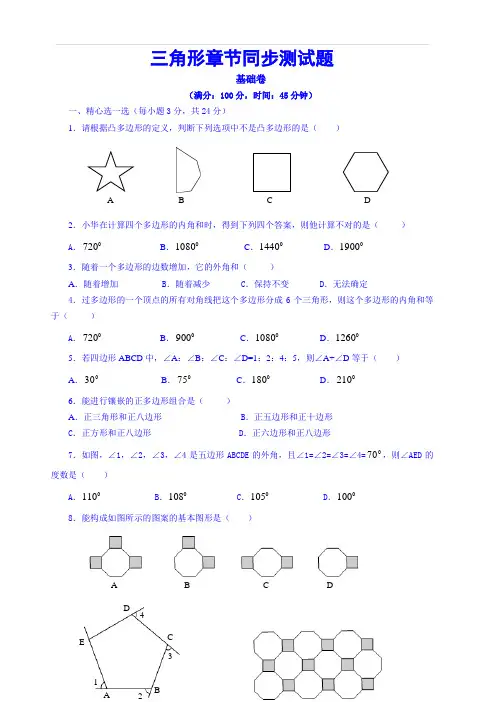
三角形章节同步测试题

基础卷

（满分：100分，时间：45分钟）

一、精心选一选（每小题3分，共24分）

1．请根据凸多边形的定义，判断下列选项中不是凸多边形的是（ ）

2．小华在计算四个多边形的内角和时，得到下列四个答案，则他计算不对的是（ ）

A．0720 B．01080 C．01440 D．01900

3．随着一个多边形的边数增加，它的外角和（ ）

A．随着增加 B．随着减少 C．保持不变 D．无法确定

4．过多边形的一个顶点的所有对角线把这个多边形分成6个三角形，则这个多边形的内角和等于（ ）

A．0720 B．0900 C．01080 D．01260

5．若四边形ABCD中，∠A：∠B：∠C：∠D=1：2：4：5，则∠A+∠D等于（ ）

A．030 B．075 C．0180 D．0210

6．能进行镶嵌的正多边形组合是（ ）

A．正三角形和正八边形 B．正五边形和正十边形

C．正方形和正八边形 D．正六边形和正八边形

7．如图，∠1，∠2，∠3，∠4是五边形ABCDE的外角，且∠1=∠2=∠3=∠4=070，则∠AED的度数是（ ）

A．0110 B．0108 C．0105 D．0100

8．能构成如图所示的图案的基本图形是（ ）

A B C

D

A B C

D

A B C D

E

1

2 3 4

二、细心填一填（每小题4分，共32分）

9．正十边形的内角和等于 度，每个内角等于 度．

第1页 共5页 第一章 全等三角形 单元检测卷

（总分100分 时间90分钟）

一、选择题（每小题3分，共30分）

1．在△ABC中，∠C＝∠B，与△ABC全等的三角形有一个角是100°，那么△ABC中与这个角对应的角是 ( )

A．∠B B．∠A C．∠C D．∠B或∠C

2．如图，已知AB＝AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是

( )

A．CB＝CD B．∠BAC＝∠DAC

C．∠BCA＝∠DCA D．∠B＝∠D＝90°

3．如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是 ( )

A．SSS B．SAS C．AAS D．ASA

4．如图，已知AB∥DC，AD∥BC，BE＝DF，则图中全等的三角形有 ( )

A．3对 B．4对 C．5对 D．6对

5．在△ABC和△DEF中，已知AB＝DE，∠A＝∠D，若补充下列条件中的任意一条，就能判定△ABC≌△DEF的是 ( )

①AC＝DF ②BC＝EF ③∠B＝∠E ④∠C＝∠F

A．①②③ B．②③④ C．①③④ D．①②④

6．在△ABC中，∠A＝90°，CD平分∠ACB，DE⊥BC于点E，若AB＝6，则DE＋DB＝ ( )

A．4 B．5 C．6 D．7

7．根据下列已知条件，能唯一画出△ABC的是 ( )

A．AB＝3，BC＝4，CA＝8 B．AB＝4，BC＝3，∠A＝30°

C．∠A＝60°，∠B＝45°，AB＝4 D．∠C＝90°，AB＝6

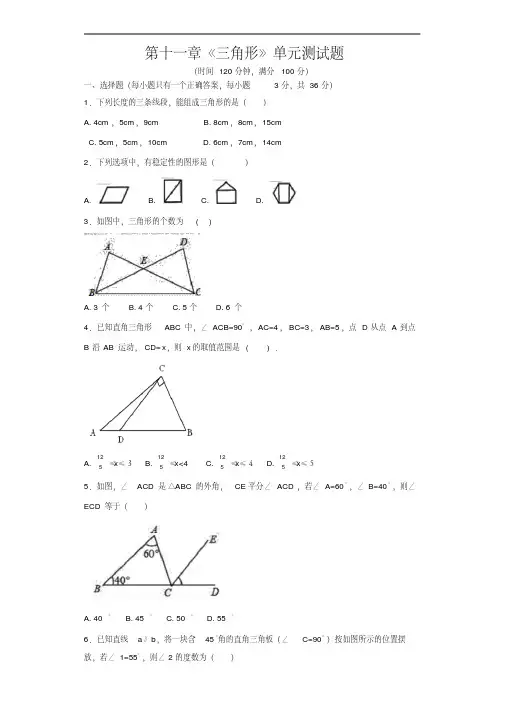
第十一章《三角形》单元测试题

（时间120分钟，满分100分）一、选择题（每小题只有一个正确答案，每小题3分，共36分）1．下列长度的三条线段，能组成三角形的是（ ）A. 4cm，5cm，9cm B. 8cm，8cm，15cm

C. 5cm，5cm，10cm D. 6cm，7cm，14cm

2．下列选项中，有稳定性的图形是（）

A. B. C. D.

3．如图中，三角形的个数为( )

A. 3个B. 4个C. 5个D. 6个

4．已知直角三角形ABC中，∠ACB=90°，AC=4，BC=3，AB=5，点D从点A到点B沿AB运动，CD=x，则x的取值范围是( ) ．

A. ≤x≤３B. ≤x<4 C. ≤x≤４D. ≤x≤５1251251251255．如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A=60°，∠B=40°，则∠

ECD等于（ ）

A. 40° B. 45° C. 50° D. 55°

6．已知直线a∥b，将一块含45°角的直角三角板（∠C=90°）按如图所示的位置摆放，若∠1=55°，则∠2的度数为（ ）

A. 80° B. 70° C. 85° D. 75°

7．如图所示，直线a∥b，∠1=35°，∠2=90°，则∠3的度数为（ ）

A. 125° B. 135° C. 145° D. 155°

8．如果一个多边形的内角和是外角和的3倍，则这个多边形的边数是（ ）

A. 8 B. 9 C. 10 D. 119．三角形的重心是三角形的（）

A. 三条中线的交点B. 三条角平分线的交点C. 三边垂直平分线的交点D. 三条高所在直线的交点

10．如图，已知在△ABC中，AD是高，若∠DAC=50°，则∠C的度数为（ ）

A. 60° B. 50° C. 40° D. 30°

11．已知实数x，y满足，则以x，y的值为两边长的等腰三角形7160xy

的周长是（ ）

A. 30或39 B. 30

C. 39 D. 以上答案均不对12．在中，，，则的形状是（）△??????∠??+∠??=134°∠??+∠??=136°△??????

第一章全等三角形检测题

（时间：90分钟，满分：100分）

一、选择题（每小题3分，共30分）

1. 在△中，∠∠，若与△全等的一个三角形中有一个角为95°，那么95°

的角在△中的对应角是（）

A. ∠

B. ∠

C.∠

D D. ∠∠

2. 下列说法正确的是（）

A.形状相同的两个三角形全等B.面积相等的两个三角形全等

C.完全重合的两个三角形全等D.所有的等边三角形全等

3.下列说法正确的个数为( )

①形状相同的两个三角形是全等三角形；②在两个三角形中，相等的角是对应角，

相等的边是对应边；③全等三角形对应边上的高、中线及对应角平分线分别相

等.

人教版数学八年级上 第十一章 《三角形》 单元检测卷（含答案）一、选择题(每题3分，共30分)1.下列各组数可能是一个三角形的边长的是( )A.1，2，4B.4，5，9C.4，6，8D.5，5，112.下列说法正确的是( )A.三角形的角平分线、中线、高都在三角形的内部B.三角形的角平分线、高都在三角形的内部C.三角形的高、中线都在三角形的内部D.三角形的角平分线、中线都在三角形的内部3.一个等腰三角形的两边长分别是3和7，则它的周长为( )A.17B.15C.13D.13或174.若从一个多边形的一个顶点出发，最多可画2014条对角线，则它是( )A.2017边形B.2016边形C.2015边形D.2014边形5.一个多边形的每个外角都等于72°，则这个多边形的边数为( )A.5B.6C.7D.86.如图，在5×4的方格纸中，每个小正方形边长为1，点O，A，B在方格纸的交点(格点)上，在第四象限内的格点上找点C，使△ABC的面积为3，则这样的点C共有( )A.2个B.3个C.4个D.5个7.如图，已知l1∥l2，∠A＝40°，∠1＝60°，则∠2的度数为( )A.40°B.60°C.80°D.100°8.如图，点O是△ABC内一点，∠A＝80°，∠1＝15°，∠2＝40°，则∠BOC等于( )A.95°B.120°C.135°D.无法确定9.如图，在锐角△ABC中，CD，BE分别是AB，AC边上的高，且CD，BE交于一点P.若∠A＝50°，则∠BPC的度数是( )A.50°B.90°C.100°D.130°10.如图，∠CBD，∠ADE为△ABD的两个外角，∠CBD＝70°，∠ADE＝149°，则∠A的度数是( )A.28°B.31°C.39°D.42°二、填空题(每题3分，共18分)11.如图，在△ABC中，∠A＝80°，点D是BC延长线上一点，∠ACD＝150°，则∠B＝______.12.如图所示，直线a∥b.直线c与直线a，b分别相交于点A，点B，AM⊥b，垂足为点M，若∠1＝58°，则∠2＝____.13.如图所示是一个起重机的示意图，在起重架中间增加了很多斜条，它所运用的几何原理是____.14.如图，在四边形ABCD中，∠A＝45°.直线l与边AB，AD分别相交于点M，N，则∠1＋∠2＝____.15.如图，若该图案是由8个相同的等腰梯形拼成的，则图中的∠1＝____.16.将一副直角三角板如图摆放，点C在EF上，AC经过点D.已知∠A＝∠EDF＝90°，AB＝AC.∠E＝30°，∠BCE＝40°，则∠CDF＝____.三、解答题(共52分)17.(8分)如图，在△ABC中，AD，AE分别是边BC上的中线和高，AE＝3cm，S△ABC＝12cm2.求BC和DC的长.18.(10分)某工程队准备开挖一条隧道，为了缩短工期，必须在山的两侧同时开挖，为了确保两侧开挖的隧道在同一条直线上，测量人员在如图所示的同一高度定出了两个开挖点Ｐ和Ｑ，然后在左边定出开挖的方向线ＡＰ，为了准确定出右边开挖的方向线ＢＱ，测量人员取一个可以同时看到点Ａ，Ｐ，Ｑ的点Ｏ，测得∠A＝28°，∠AOC＝100°，那么∠QBO应等于多少度才能确保ＢＱ与ＡＰ在同一条直线上？19.(10分)如图，∠B＝45°，∠A＋15°＝∠1，∠ACD＝60°.求证：AB∥CD.20.(12分)(1)已知等腰三角形的一边等于6cm，一边等于7cm，求它的周长；(2)已知等腰三角形的一边长为5cm，周长为20cm，求其他的边长.21.(12分)如图所示，在四边形ABCD中，∠A与∠C互补，BE平分∠ABC，DF平分∠ADC.若BE∥DF，求证：△DCF为直角三角形.参考答案1.C2.D3.A4.A5.A6.B7.C8.C9.D10.C11.70°12.32°13.三角形具有稳定性14.225°15.67.5°16.25°17.∵S△ABC＝21BC·AE＝21cm2,AE＝3cm,∴BC＝8cm.∵AD是BC边上的中线,∴DC＝21BC＝4cm.18.在△AOB中，∠ＱＢＯ＝180°－∠Ａ－∠Ｏ＝180°－28°－100°＝52°.即∠QBD应等于52°才能确保BQ与AP在同一条直线上.19.证明：∵∠B＝45°，∠A＋15°＝∠1，∴在△ABC中，∠A＋∠A＋15°＋45°＝180°.∴∠A＝60°.∵∠ACD＝60°，∴∠A＝∠ACD.∴AB∥CD.20.(1)当6cm长为腰长时，三边长为6cm，6cm，7cm,则周长为19cm；当7cm长为腰长时，三边长为6cm，7cm，7cm，则周长为20cm.所以这个等腰三角形的周长为19cm或20cm.(2)当5cm长为腰长时，三边长为5cm，5cm，10cm，∵5＋5＝10，∴5cm不可能为腰长；当5cm长为底边长时，三边长为5cm，7.5cm和7.5cm.所以这个等腰三角形的边长分别为5cm，7.5cm和7.5cm.21.证明：∵在四边形ABCD中，∠A与∠C互补，∴∠ABC＋∠ADC＝180°.又∵BE平分∠ABC，DF平分∠ADC，∴∠EBC＋∠FDC＝90°.∵BE∥DF,∴∠EBC＝∠DFC.∴∠DFC＋∠FDC＝90°.∴△DCF为直角三角形.

第1页 共7页 三角形综合应用（讲义）

 知识点睛

在三角形背景下处理问题的思考方向：

1. 三角形中的隐含条件是：

边：_______________________________________________．

角：①______________________________________________；

②_____________________________________________．

2. 角平分线出现时，为了计算方便，通常采用__________解决问题．

3. 高线出现时考虑__________或__________．

 精讲精练

1. 现有3 cm，4 cm，7 cm，9 cm长的四根木棒，任取其中三根组成一个三角形，那么可以组成的三角形的个数是（ ）

A．1个 B．2个 C．3个 D．4个

2. 如图，用四个螺丝将四条不可弯曲的木条围成一个木框，不计螺丝大小，其中相邻两螺丝的距离依次为2，3，4，6，且相邻两木条的夹角均可调整．若调整木条的夹角时不破坏此木框，则任两螺丝之间的距离最大值是（ ）

A．5 B．6 C．7 D．10

3. 下列五种说法：①三角形的三个内角中至少有两个锐角；

②三角形的三个内角中至少有一个钝角；③一个三角形中，至少有一个角不小于60°；④钝角三角形中，任意两个内角的和必大于90°；⑤直角三角形中两锐角互余．其中正确的说法有__________________（填序号）．

4. 如图，在三角形纸片ABC中，∠A=60°，∠B=55°．将纸片一角折叠使点C落在△ABC内，则∠1+∠2=_________．

BC21A ABCDE

第4题图 第5题图

5. 如图，一个五角星的五个角的和是________．

6. 如图，∠A+∠B+∠C+∠D+∠E+∠F=________． 6432第2题图

2019-2020学年 第十一章三角形单元测试

一、单选题（共10题；共30分）

1、如图，小正方形边长为1，连结小正方形的三个顶点，可得△ABC，则AC边上的高是（ ）

A、 B、 C、 D、

2、等腰三角形的两边分别为5cm、4cm，则它的周长是（ ）

A、14cm B、13cm C、16cm或9cm D、13cm或14cm

3、若一个多边形有14条对角线，则这个多边形的边数是（ ）

A、10 B、7 C、14 D、6

4、在四边形的内角中，直角最多可以有（ ）

A、1个 B、2个 C、3个 D、4个

5、一个多边形的内角和是720°，则这个多边形的边数为（ ）

A、4 B、5 C、6 D、7

6、下列图形中有稳定性的是（ ）

A、正方形 B、直角三角形 C、长方形 D、平行四边形

7、八边形的对角线共有（ ）

A、8条 B、16条 C、18条 D、20条

8、多边形的每个内角都等于150°，则从此多边形的一个顶点出发可作的对角线共有（ ）

A、8条 B、9条 C、10条 D、11条

2019-2020学年 9、若一个多边形的外角和与它的内角和相等，则这个多边形是（ ）

A、三角形 B、五边形 C、四边形 D、六边形

10、如图，在证明“△ABC内角和等于180°”时，延长BC至D，过点C作CE∥AB，得到∠ABC=∠ECD，∠BAC=∠ACE，由于∠BCD=180°，可得到∠ABC+∠ACB+∠BAC=180°，这个证明方法体现的数学思想是（ ）

A、数形结合 B、特殊到一般 C、一般到特殊 D、转化

人教版数学八年级上学期

《三角形》单元测试

(时间：120分钟 满分：150分)

一．选择题（共10小题）

1.课堂上，老师把教学用的两块三角板叠放在一起，得到如图所示的图形，其中三角形的个数为（ ）

A. 2 B. 3 C. 5 D. 6

2.如图，BD是△ABC的高，EF∥AC，EF交BD于G，下列说法正确的有（ ）

①BG是△EBF的高；②CD是△BGC的高；③DG是△AGC的高；④AD是△ABG的高．

A. 1个 B. 2个 C. 3个 D. 4个

3.下列说法正确的是（ ）

A. 三角形的三条中线交于一点 B. 三角形的三条高都在三角形内部

C. 三角形不一定具有稳定性 D. 三角形的角平分线可能在三角形的内部或外部

4.下列线段长能构成三角形的是（ ）

A. 3、4、8 B. 2、3、6 C. 5、6、11 D. 5、6、10

5.一个缺角的三角形ABC残片如图所示，量得∠A＝60°，∠B＝75°，则这个三角形残缺前的∠C的度数为（ ）

A. 75° B. 60° C. 45° D. 40°

6.如图，在△ABC中，∠A＝80°，点D在BC的延长线上，∠ACD＝145°，则∠B是（ ）

A. 45° B. 55° C. 65° D. 75°

7.已知直角三角形ABC，有一个锐角等于50°，则另一个锐角的度数是（ ）

A. 30° B. 40° C. 45° D. 50°

8.将一个四边形截去一个角后，它不可能是（ ）

A. 六边形 B. 五边形 C. 四边形 D. 三角形

9.如果n边形的内角和是它外角和的4倍，则n等于（ ）

A. 7 B. 8 C. 10 D. 9

10.如图，小明从A点出发，沿直线前进10米后向左转36°，再沿直线前进10米，再向左转36°……照这样走下去，他第一次回到出发点A点时，一共走的路程是（ ）

人教版八年级上册《三角形》单元测试卷

(时间：120分钟 满分：150分)

一、选择题（本大题共10小题,共30.0分）

1.如图,在△A B C 中,A D 是B C 边上的高,B E平分∠A B C 交A C 边于E,∠B A C =60°,∠A B E=25°,则∠D A

C 的大小是（ ）

学,科,网...

A . 15° B . 20° C . 25° D . 30°

2.如图,将△A B C 沿D E,EF翻折,顶点A ,B 均落在点O处,且EA 与EB 重合于线段EO,若∠D OF=142°,则∠C 的度数为（ ）

A . 38° B . 39° C . 42° D . 48°

3.如图,A D 是△A B C 的外角∠C A E的平分线,∠B =30°,∠D A E=55°,则∠A C B 的度数是（ ）

A . 80° B . 85° C . 100° D . 110°

4.如图,在△A B C 中,以点B 为圆心,以B A 长为半径画弧交边B C 于点D ,连接A D ．若∠B =40°,∠C =36°,则∠D A C 的度数是（ ）

A . 70° B . 44° C . 34° D . 24° 5.如图,在△A B C 中,∠A C B =100°,∠A =20°,D 是A B 上一点,将△A B C 沿C D 折叠,使B 点落在A C 边上的B ′处,则∠A D B ′等于（ ）

A . 40° B . 20° C . 55° D . 30

6.如图,△A B C 中,B D 、B E分别是高和角平分线,点F在C A 的延长线上,FH⊥B E,交B D 于点G,交B C

于点H．下列结论：①∠D B E＝∠F； ②2∠B EF＝∠B A F＋∠C ；③∠F＝∠B A C －∠C ；④∠B

部编版语文八年级上学期

第三单元综合测试

时间：90分钟 满分：100分

一、积累(20分)

1.下边句子朗读节奏划分有误的一项是(2分)( )

A.自/三峡七百里中 B.未复有/能与其奇者

C.但少闲人/如吾两人者耳 D.蝉则/千转不穷

2.解释下列句中加点词语的古义和今义.(4分)

(1)良．多趣味 古义： ；今义：

(2)晓雾将歇． 古义： ；今义：

(3)但少闲人如吾两人者耳． 古义： ；今义：

(4)蝉则千转不穷． 古义： ；今义：

3.解释下列句中加点词语的意思.(4分)

(1)绝．巘多生怪柏( ) 天下独绝．( )

(2)自．非亭午夜分( ) 自．康乐以来( )

(3)未复有能与．其奇者( ) 相与．步于中庭( )

(4)负势竞上．( ) 横柯上．蔽( )

4.古诗文名句默写.(7分)

(1) ,山山唯落晖.(王绩《野望》)

(2)山随平野尽, .(李白《渡荆门送别》)

(3) ,四时俱备.(陶弘景《答谢中书书》)

(4)崔颢在《黄鹤楼》一诗中情景交融,抒发了游子悲苦的思乡之情的诗句是：

第1页共4页三角形综合应用（习题）

例题示范

例1：如图，BD，CD分别平分∠ABC，∠ACB，CE⊥BD交BD的延长线于点E．

求证：∠DCE=∠CAD．

DE

CBA

【思路分析】

①看到条件BD，CD平分∠ABC，可知AD也平分∠BAC，得到：1

2DACBAC，

1

2DBCABC，1

2DCBACB；

②根据CE⊥BD，得90DEC

，所以90DCEEDC

；

③题目所求为∠DCE=∠CAD，若能够说明90CADEDC

即可；

④根据三角形的内角和定理得：180BACABCACB

，所以

90CADDBCDCB，再根据三角形的外角定理可知

EDCDBCDCB，所以90CADEDC，证明成立．

【过程书写】

证明：如图，

∵BD，CD分别平分∠ABC，∠ACB

∴1

2DACBAC，1

2DBCABC，1

2DCBACB

在△ABC中，180BACABCACB

∴90CADDBCDCB

∵∠EDC是△BCD的一个外角

∴EDCDBCDCB

∴90CADEDC

∵CE⊥BE

∴90DEC

∴90DCEEDC

∴∠DCE=∠CAD

巩固练习

1.现有2 cm，4 cm，6 cm，8 cm长的四根木棒，任意选取三根组成一个三角形，

那么可以组成三角形的个数为（）

A．1个B．2个C．3个D．4个DE

CBA