下载文档原格式
向量的投影与正交在线性代数中，向量的投影和正交是非常重要的概念。
它们不仅可以帮助我们理解向量的性质，还可以应用于实际问题的求解。
本文将详细介绍向量的投影和正交的概念、性质以及应用。
一、向量的投影向量的投影是指一个向量在另一个向量上的投影长度。
对于两个向量A和A，如果我们希望计算向量A在向量A上的投影长度，可以通过以下方法进行计算：1. 计算向量的点积：将向量A和向量A的点积除以向量A的模长的平方。
2. 将结果乘以向量A：将步骤1中得到的结果乘以向量A，即可得到向量A在向量A上的投影向量。
向量的投影可以帮助我们理解两个向量之间的关系。
如果两个向量的投影为零，则它们是正交的；如果两个向量的投影长度相等，则它们是平行的。
二、向量的正交向量的正交是指两个向量之间的夹角为90度。
如果两个向量的点积等于零，则它们是正交的。
点积是通过将两个向量的对应分量相乘，并将相乘的结果相加而得到的。
正交向量具有许多重要的性质。
例如，如果两个向量是正交的，则它们的张成空间也是正交的。
这可以用来解决一些实际问题，比如线性回归中的多重共线性问题。
三、向量投影与正交的应用向量的投影和正交在实际问题中有广泛的应用。
以下是一些常见的应用场景：1. 图像处理：在图像处理中，向量的投影可以用来进行图像压缩和降噪处理。
通过计算图像中像素点的投影长度，可以提取出图像中的主要特征，并减少噪声的影响。
2. 三维图形学：在三维图形学中，向量的投影和正交被广泛应用于图形的旋转、变换和投影等计算中。
通过计算物体在不同坐标轴上的投影长度，可以实现物体在三维空间中的变换和投影效果。
3. 机器学习：在机器学习中，向量的正交可以用于特征选择和降维。
通过找到数据集中相互正交的特征向量，可以提取出最具有代表性的特征，从而提高机器学习算法的准确性和效率。
综上所述，向量的投影和正交是线性代数中重要的概念。
通过理解和应用向量的投影和正交，我们可以更好地理解向量的性质，并将其应用于实际问题的求解中。
线性代数教学教案第3章 向量与向量空间授课序号01 教 学 基 本 指 标教学课题 第3章 第1节 维向量及其线性运算课的类型 新知识课 教学方法 讲授、课堂提问、讨论、启发、自学教学手段 黑板多媒体结合 教学重点 维向量的概念、向量的线性运算的性质教学难点 向量的线性运算的性质 参考教材 同济版《线性代数》作业布置 课后习题大纲要求 理解维向量的概念 教 学 基 本 内 容一． 维向量的概念1．维向量：由个数组成的有序数组称为维向量.2．称为维行向量，称为维列向量. 二．维向量的线性运算1．定义：（1）分量全为0的向量称为零向量；（2）对于，称为的负向量； （3）对于，，当且仅当时，称与相等；（4）对于，，称为与的和；（5）对于，，称为与的差； （6）对于，为实数，称为的数乘，记为.2．向量的线性运算的性质：对任意的维向量和数，有：n n n n n n n a a a ,,,21 n ),,,(21n a a a n 12⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦n a a a n n ()12T n αa ,a ,,a = ()12---Tn a ,a ,,a αT n a a a ),,,(21 =αT n b b b ),,,(21 =β),,2,1(n i b a i i ==αβT n a a a ),,,(21 =αT n b b b ),,,(21 =βT n n b a b a b a ),,,(2211+++ αβT n a a a ),,,(21 =αT n b b b ),,,(21 =β()1122---Tn n a b ,a b ,,a b αβT n a a a ),,,(21 =αk T n ka ka ka ),,,(21 ααk n γβα，，l k ,（1）;（2）;（3）;（4）;（5）;（6）;（7）；（8）.三．例题讲解例1． 某工厂两天的产量(单位:吨)按照产品顺序用向量表示,第一天为第二天为求两天各产品的产量和.αββα+=+)()(γβαγβα++=++αα=+00-αα=αα=⋅1αα)()(kl l k =βαβαk k k +=+)((k l )αk αl α+=+1(15,20,17,8),=T α2(16,22,18,9),=T α授课序号02 教 学 基 本 指 标教学课题 第3章 第2节 向量组的线性关系 课的类型 新知识课 教学方法 讲授、课堂提问、讨论、启发、自学 教学手段 黑板多媒体结合教学重点 线性组合与线性表示、向量组线性相关、线性无关的定义，向量组线性相关、线性无关的有关性质及判别法教学难点 有关线性相关、线性无关的证明 参考教材 同济版《线性代数》作业布置 课后习题大纲要求 1．理解向量的线性组合与线性表示。
线性代数中的正交补与正交投影线性代数是数学中的一个重要分支，研究向量空间以及线性变换等概念和性质。
正交补与正交投影是线性代数中的两个重要概念，对于理解向量空间的性质和线性变换的特性具有重要意义。
一、正交补在线性代数中，给定一个向量空间V，如果存在一个向量空间W，使得W中的任意向量与V中的任意向量的内积为零，则称W为V的正交补，记作$W=V^{\perp}$。
在实向量空间中，正交补的概念更加容易理解。
例如，对于平面内的一个向量空间V，它的正交补W就是与V所张成的平面垂直的那条直线。
而对于三维空间，V的正交补W则是与V所张成的平面垂直的那个平面。
对于一个向量空间V，它的维数为n，则它的正交补的维数为m = dim(V) - dim(W)。
正交补的维数可以帮助我们判断向量空间的性质以及进行相关计算。
二、正交投影正交投影是线性代数中一个重要的概念，它可以帮助我们理解向量空间中的投影操作。
在给定一个向量空间V和一个向量v时，正交投影可以将向量v投影到V上。
具体而言，对于一个向量空间V和一个向量v，V的正交补空间为$V^{\perp}$。
我们想要将向量v在V上进行投影，可以通过正交补空间来实现。
投影操作的思想是，我们将向量v拆分成V上的一个分量和V的正交补空间上的一个分量。
其中，V上的分量可以称为正交投影。
正交投影的计算公式如下：$$P_V=\frac{v\cdot u}{u\cdot u}u$$其中，$u$为向量空间V上的一个向量，$v$为待投影的向量。
计算得到的正交投影向量$P_V$与向量空间V中的每个向量都正交，并且长度最短。
正交投影的概念和计算方法在实际应用中经常被使用。
例如，在计算机图形学中，正交投影可以帮助我们实现三维物体在二维屏幕上的投影效果。
三、应用实例1. 线性回归中的正交多项式回归在统计学中，线性回归是一种重要的数据分析方法。
当我们需要对多项式进行回归时，可以使用正交多项式回归方法。
正交多项式回归通过寻找一组正交多项式作为基函数，将输入数据在这组基函数上进行投影。
高等数学线性代数教材目录第一章行列式1.1 行列式的引入1.2 二阶和三阶行列式的计算1.3 行列式的性质和性质的应用1.4 行列式的性质证明第二章矩阵和向量2.1 矩阵的概念和基本运算2.2 矩阵的转置和逆2.3 向量的线性相关性和线性无关性2.4 向量组的秩和极大线性无关组第三章矩阵的运算3.1 矩阵的加法和减法3.2 矩阵的数乘3.3 矩阵的乘法3.4 矩阵的特殊类型第四章线性方程组4.1 线性方程组的概念和解的分类4.2 齐次线性方程组和非齐次线性方程组的解 4.3 线性方程组的向量表示第五章向量空间5.1 向量空间的定义和例子5.2 向量子空间和子空间的概念5.3 向量空间的线性组合和生成子空间5.4 基和维数第六章矩阵的特征值和特征向量6.1 特征值和对角化6.2 特征多项式和特征方程6.3 相似矩阵和相似对角矩阵6.4 实对称矩阵的对角化第七章线性变换7.1 线性变换的概念和性质7.2 线性变换的矩阵表示7.3 线性变换的特征值和特征向量7.4 线性变换的相似、迹和行列式第八章内积空间8.1 内积的定义和性质8.2 欧几里得空间和具有内积的实向量空间8.3 向量的正交性和正交子空间8.4 施密特正交化方法第九章广义特征值问题9.1 广义特征值问题的引入9.2 广义特征值的计算9.3 广义特征值与相似变换9.4 对称矩阵的广义特征值问题与对角化第十章特殊矩阵的标准形式10.1 对称矩阵的对角化10.2 正定矩阵和正定二次型10.3 实对称矩阵的正交对角化10.4 复数矩阵的标准型这是《高等数学线性代数》教材的目录, 包含了十个章节，每个章节中有相应的小节来详细介绍相关内容。
这本教材综合了高等数学和线性代数的知识，旨在帮助读者掌握线性代数的基本概念、理论和方法，以及应用于实际问题的能力。
希望读者通过学习这本教材，能够系统地理解和应用线性代数的知识，为今后的学习和研究打下坚实的基础。
高等代数知识点高等代数是大学数学专业的一门核心课程，主要研究线性代数的更深层次的内容和推广。
它是数学中的一门基础学科，对于很多数学分支都有着重要的应用。
下面是高等代数的主要知识点：1.向量空间理论：向量空间是高等代数的核心概念之一、它研究向量的基本性质和运算规律，包括向量的加法、数乘、内积、外积等。
2.线性变换和矩阵理论：线性变换是向量空间中的一个重要概念，它是一种保持向量加法和数乘运算的函数。
矩阵是线性变换在两个有限维向量空间基下的坐标矩阵表示。
3.特征值和特征向量：特征值和特征向量是线性变换中重要的概念，它们描述了一个线性变换在一些向量上的作用。
特征值是一个标量，特征向量是满足特定条件的非零向量。
4.行列式和特征多项式：行列式是一个方阵所确定的一个标量值，它描述了一个矩阵的一些特征。
特征多项式则是通过行列式来描述一个线性变换的特征。
5.正交性和正交矩阵：正交性是线性代数中重要的概念，它描述了向量空间中向量的垂直性质。
正交矩阵是一种特殊的方阵，它的列向量两两正交并且长度为16.线性方程组：线性方程组是高等代数中一个基本的研究对象。
通过矩阵的运算和消元法可以求解线性方程组的解。
7.广义逆矩阵和正规方阵：广义逆矩阵是矩阵理论的重要扩展，它在未必是方阵的情况下，求解矩阵方程和线性方程组具有重要应用。
正规方阵则是满足一定条件的方阵。
8.特殊矩阵：特殊矩阵是高等代数中特别重要的一类矩阵，包括对角矩阵、上三角矩阵、下三角矩阵、对称矩阵、反对称矩阵等。
9.特征值分解和奇异值分解：特征值分解是一种将线性变换表示成特征向量和对应特征值的形式的方法，奇异值分解则是一种将矩阵表示成特征值和特征向量的形式的方法。
10. Jordan标准形和Schur分解：Jordan标准形是复矩阵的一种标准形式，它可以将复矩阵进行相似变换后表示成一个特殊的形式。
Schur分解是一种将矩阵表示成三角形的形式的方法。
这些是高等代数的主要知识点，掌握了这些知识点，就能够理解和应用高等代数的基本原理和方法，为后续更深入的数学学习打下坚实的基础。
同济大学线性代数第六版正交向量与正交矩阵的性质正交向量和正交矩阵是线性代数中非常重要的概念，它们在各个领域中都有着广泛的应用。
在同济大学线性代数教材的第六版中，正交向量和正交矩阵的性质被详细地介绍和讲解。
本文将围绕这一主题展开，探讨正交向量和正交矩阵的性质及其应用。
一、正交向量的性质正交向量是指两个向量的内积为零，也就是说它们的夹角为九十度。
同济大学线性代数第六版中详细介绍了正交向量的性质。
首先，正交向量的数量不会超过向量空间的维数。
这一性质被称为正交向量的基本定理，它对于解决线性方程组和矩阵的特征值问题非常重要。
其次，同济大学线性代数第六版还介绍了正交向量组和正交补空间的概念。
正交向量组是指一组两两正交的向量，它们张成的子空间被称为正交子空间。
而正交补空间是指与一个向量空间正交的向量构成的子空间。
正交补空间的概念在矩阵和线性方程组的求解中经常出现，可以帮助我们简化问题，降低计算难度。
二、正交矩阵的性质正交矩阵是指方阵的转置矩阵等于其逆矩阵的矩阵。
同济大学线性代数第六版中详细介绍了正交矩阵的性质及其应用。
首先，正交矩阵的行向量组和列向量组都是正交向量组。
这一性质使得正交矩阵具有很好的几何意义，可以用来描述旋转和镜像。
其次，同济大学线性代数第六版介绍了正交矩阵的特殊形式——正交对角矩阵。
正交对角矩阵的对角线上的元素都是1或-1，其余元素都是0。
正交对角矩阵具有简单的性质和运算规则，在计算中比较方便。
另外，同济大学线性代数第六版还介绍了正交复合矩阵的概念。
正交复合矩阵是由多个正交矩阵相乘得到的，具有一些特殊的性质。
例如，正交复合矩阵的转置等于其逆矩阵，因此可以保证矩阵乘法的可逆性。
三、正交向量和正交矩阵的应用正交向量和正交矩阵在各个领域中都有着广泛的应用。
首先，在几何学中，正交向量可以用来描述平面和空间中的垂直关系，例如描述直线的法向量，计算投影和距离等。
其次，在物理学中，正交向量和正交矩阵经常用于描述旋转、镜像和坐标变换等问题。
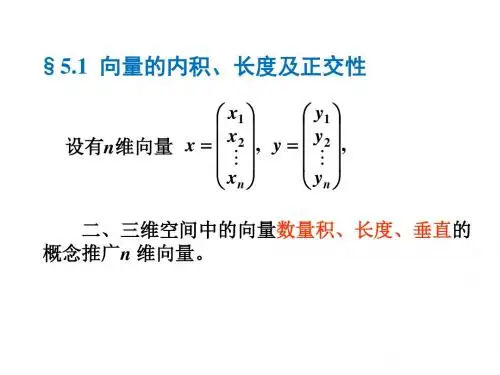
线性代数中正交变换与对角化线性代数是数学中的一个重要分支，它研究的是向量空间及其线性变换。
正交变换和对角化是线性代数中的两个重要概念，它们在矩阵理论、物理学、工程学等领域中具有广泛的应用。
本文将深入探讨线性代数中的正交变换和对角化。
1. 正交变换正交变换是指保持向量的长度和两向量之间的夹角不变的线性变换。
具体来说，设T为一个线性变换，如果对于任意向量u和v，有内积⟨Tu, Tv⟩ = ⟨u, v⟩，则称T为正交变换。
在二维空间中，常见的正交变换有旋转和翻转。
旋转变换保持向量的长度不变，翻转变换则改变向量的方向。
在三维空间中，正交变换可以通过矩阵表示。
一个3×3的实数矩阵A如果满足A^T · A = I（式中 I 是单位矩阵），则称A为正交矩阵。
正交矩阵表示了三维空间中的旋转和翻转变换。
2. 对角化对角化是线性代数中另一个重要的概念，它是指通过选择合适的坐标系，使得线性变换的矩阵表示具有对角形式。
具体来说，设T为一个线性变换，如果存在一个可逆矩阵P，使得P^-1 · A · P = D（式中 A 是线性变换T的矩阵表示，D是对角矩阵），则称T是可对角化的。
对角化的一个重要应用是简化线性变换的计算。
对于可对角化的线性变换，我们可以通过对角矩阵D来计算其作用，而不需要直接计算线性变换的矩阵表示。
这在很多实际问题中具有重要意义。
3. 正交变换与对角化的关系在线性代数中，正交矩阵具有非常有用的性质。
如果一个矩阵是正交矩阵，那么它的逆等于它的转置，即A^-1 = A^T。
这意味着一个正交矩阵同时也是一个酉矩阵（复数域上的正交矩阵）。
对于一个实对称矩阵，我们可以通过正交变换将其对角化。
具体来说，设A是一个实对称矩阵，存在正交矩阵P，使得P^-1 · A · P = D，其中D是对角矩阵。
对角矩阵的对角元素恰好是矩阵A的特征值，而P的列向量是对应的特征向量。
线性代数中的正交变换与正交矩阵线性代数是数学的一个重要分支，其中的正交变换与正交矩阵是其核心概念之一。
本文将详细探讨正交变换与正交矩阵的定义、性质以及应用。
一、正交变换的定义和性质在线性代数中，正交变换指的是在向量空间中保持向量长度和夹角不变的线性变换。
具体而言，给定一个向量空间V和其上的内积，一个线性变换T称为正交变换，如果对于任意的向量x和y，其满足内积不变性：⟨Tx, Ty⟩ = ⟨x, y⟩正交变换具有以下性质：1. 正交变换保持向量的长度不变，即对于向量x，有∥Tx∥ =∥x∥。
2. 正交变换保持向量之间的夹角，即对于向量x和y，有⟨Tx, Ty⟩= ⟨x, y⟩。
3. 若正交变换T将向量x映射为零向量，则原向量x也为零向量。
二、正交矩阵的定义和性质正交矩阵是一个满足以下条件的方阵：1. 矩阵的每一列都是单位向量。
2. 任意两列之间的内积等于零，即矩阵的列向量两两正交。
3. 矩阵的每一行都是单位向量。
4. 矩阵的转置等于其逆矩阵，即A^T A = AA^T = I。
正交矩阵具有以下性质：1. 正交矩阵的行向量组也为正交向量组。
2. 正交矩阵的列向量组也为正交向量组。
3. 正交矩阵的转置矩阵也是正交矩阵。
4. 正交矩阵的行列式的值为±1。
三、正交变换与正交矩阵的应用正交变换和正交矩阵在许多领域中都有广泛的应用，以下列举其中的几个重要应用：1. 几何变换：正交变换可以用来进行平移、旋转和镜像等几何变换操作。
例如，二维平面上的旋转可以通过乘以一个旋转矩阵实现。
2. 物体建模：在计算机图形学中，正交矩阵常用于表示物体的旋转和缩放变换，用来实现物体模型的变换和渲染。
3. 信号处理：正交矩阵可以用来对信号进行变换和分析，如傅里叶变换和卡拉OK变换。
4. 数据压缩：正交矩阵可以用于数据压缩领域，例如JPEG图像压缩中的离散余弦变换。
5. 特征值问题：正交变换与正交矩阵在求解特征值问题中起到关键作用，例如用于主成分分析和奇异值分解等。
