六年级列方程解决问题总复习

小学六年级列方程解决问题题型总结标题：小学六年级列方程解决问题题型总结字数要求：800字以上摘要：本文总结了小学六年级列方程解决问题的题型，包括等量代换法、运用“代数法”解决问题、常见的列方程解决问题等。

正文：一、等量代换法等量代换法是一种常用的解决问题的方法，通常用于列方程解决问题。

具体步骤如下：1. 读题理解，确定未知量和已知量；2. 在问题中设未知量为x，根据问题条件，用x表示已知量；3. 列方程，建立x与其他已知量之间的关系；4. 解方程，找到未知量x的值；5. 检查答案是否符合题意。

二、运用“代数法”解决问题运用“代数法”解决问题，也是一种常见的方法，可用于列方程解决问题。

具体步骤如下：1. 读题理解，确定未知量和已知量；2. 在问题中设未知量为x或其他字母，根据问题条件，用x或其他字母表示已知量；3. 列方程，建立未知量与其他已知量之间的关系；4. 解方程，找到未知量的值；5. 检查答案是否符合题意。

三、常见的列方程解决问题在小学六年级的数学研究中，存在一些常见的题型，可通过列方程解决，例如：1. “一共n个苹果，小明拿了5个，小强拿了3个，还剩几个？”2. “小红头发有x根，小明头发有y根，他们的头发一共有多少根？”3. “A班有x个学生，B班比A班多5个学生，一共有多少学生？”通过对这些题型的列方程解决，可以帮助学生提高解决问题的能力和运用代数的能力。

结论：通过掌握等量代换法、运用“代数法”解决问题以及常见的列方程解决问题题型，小学六年级的学生可以更好地理解和解决数学问题，提高数学思维能力和运用代数的能力。

六年级数学解决问题复习1、车队向灾区运送一批救灾物资，去时每小时行80km，5小时到达灾区。

回来时每小时行100km，这支车队要多长时间能够返回出发地？2、书店有一套科普丛书原价96元，现按6折出售，买一套可以便宜多少元？如果买6套，360元够吗？3、邮局汇款的汇率是1%，在外打工的小明的爸爸给家里汇钱，一共交了38元的汇费，小明的爸爸一共给家里汇了多少元？4、汽车厂计划25天组装汽车4000辆，实际提前5天完成，实际平均每天组装汽车多少辆？（用方程解）5、一个长方体玻璃鱼缸（鱼缸的上面没有玻璃），长5分米，宽3分米，高3.5分米。

制作这个鱼缸至少需要多少平方分米的玻璃？7、一个底面半径是6厘米的圆柱形玻璃器皿里装有一部分水，水中浸没着一个高9厘米的圆锥体铅锤。

当铅锤从水中取出后，水面下降了0.5厘米。

这个圆锥体的底面积是多少平方厘米？（π取3.14）8、一个食堂十一月份烧煤50吨，比原计划节约了5吨，节约了百分之几？9、学校数学小组的人数比美术小组的人数多20%，如果数学小组有30人，那么美术小组有多少人？（列方程解答）10、小华将4000元存入银行，定期2年，如果按月利率为0.25%计算的话，到期后应得利息多少元？缴纳5%的利息税后，一共可取回多少钱？11、一套西服共320元，裤子的单价是上衣单价的60%，求上衣的单价比裤子的单价多多少元？12、大厅里有8根圆柱形木桩要刷油漆，木桩底面周长2.5米，高4.2米，1千克的油漆可以漆6平方米，那么刷这些木桩要多少油漆？13、张爷爷用篱笆围成如图养鸡场，一边利用房屋墙壁，篱笆长35米，求养鸡场面积？14、用72块方砖铺了18平方米，那么铺24平方米，要这样的方砖几块？(用比例解)15、农机厂计划生产800台，平均每天生产44台，生产了10天，余下的任务要求8天完成，平均每天要生产多少台？16、一间教室要用方砖铺地。

用边长是3分米的正方形方砖，需要960块，如果改用边长为2分米的正方形方砖，需要多少块？（用比例解）17、红星小学去年有毕业生250人，今年比去年毕业生人数多2%。

列方程解应用题专项练习卷甲、乙、丙三条铁路共长1191千米，甲铁路长比乙铁路的2倍少189千米，乙铁路长比丙铁路少8千米，求甲铁路的长．一个工程队由6个粗木工和1个细木工组成．完成某项任务后，粗木工每人得200元，细木工每人工资比全队的平均工资多30元．求细木工每人得多少元．提示设细木工每人得x元，那么全队的平均工资是(x—30)元．这样全队总工资可由两个式子表示：7(x—30)或(200×6+x)．小明期中考试语文、数学、地理三科平均分为96分，常识分数比语文、数学、地理、常识四科平均分少3分．求常识分数．电视机厂装配一批电视机，计划25天完成，如每天多装35台，24天能超额完成60台．求原计划每天装配多少台．师徒俩要加工同样多的零件，师傅每小时加工50个，比徒弟每小时多加工10个．工作中师傅停工5小时，因此徒弟比师傅提前1小时完成任务．求两人各加工多少个零件．买2．5千克苹果和2千克橘子共用去13．6元，已知每千克苹果比每千克橘子贵2．2元，这两种水果的‘单价各是每千克多少元?买4支钢笔和9支圆珠笔共付24元，已知买2支钢笔的钱可买3支圆珠笔，两种笔的价钱各是多少元?一个两位数，个位上的数字是十位上数字的2倍，如果把十位上的数字与个位上的数字对调，那么得到的新两位数比原两位数大36．求原两位数．提示可以设原两位数的十位上的数字为x，那么个位上的数字是2x。

原两位数可表示为(10x+2x)，而新两位数可用(2x·10+x)表示．一个两位数，十位上的数字比个位上的数字小1，十位上的数字与个位上的数字的和是这个两位数的0．2倍．求这个两位数．有四只盒子，共装了45个小球．如变动一下，第一盒减少2个；第二盒增加2个；第三盒增加一倍；第四盒减少一半，那么这四只盒子里的球就一样多了．原来每只盒子中各有几个球?提示由于现在各盒中球的个数都相等，因此可设现在每只盒子中各有x个球，再写出原来各盒中球的个数分别为(x—2)个、(x+2)个、(x÷2)个、2x个。

南山实验学校六年级数学学科导学案课题：列方程解决行程问题主备人：李莉班级: 学生姓名：学习目标：1、会借助“线段图”分析行程问题中的相遇、追及问题，并能根据线段图找出等量关系。

2、会列方程解决行程（相遇、追及）问题。

目标三：追及问题例题：甲、乙两车自西向东行驶，甲车的速度是每小时48千米，乙车的速度是每小时72千米，甲车开出2小时后乙车开出，问几小时后乙车追上甲车？分析：设x小时后乙车追上甲车。

甲车先行2小时的路程（48×2）甲车x小时所行的路程（48x）乙车x小时所行的路程(72x)从图上可以看出的等量关系是，我们可以根据这个等量关系列出方程：解法如下：解：设x小时后乙车追上甲车。

答：小时后乙车追上甲车。

【自学检测】（先用线段图分析等量关系，再列方程解答）甲、乙两位同学练习赛跑，甲每秒跑7米，乙每秒跑6.5米。

如果甲让乙先跑1秒，几秒钟后甲可以追上乙？线段图：等量关系：解：设一、学、议环节目标一：解行程问题的应用题要用到路程、速度、时间之间的关系，如果用s、v、t分别表示路程、速度、时间，那么s、v、t三个量的关系为s= ，或v= ，或t= 。

目标二：相遇问题例题： A、B两地相距960千米，甲、乙两辆汽车分别从两地同时出发，相向开出，6小时后两车相遇；已知甲车的速度是乙车的倍。

求甲、乙两车的速度各是多少？B速度：1.5千米／时甲车6小时所行的路程乙车6小时所行的路程分析：如上图，设一倍数（乙车）的速度是x千米／时，那么甲车的速度就是1.5x千米／时。

从图上可以看出的等量关系是，我们可以根据这个等量关系列出方程：解法如下：解：设乙车的速度是x千米／时，那么甲车的速度就是1.5x千米／时。

答：甲的速度是千米／时，乙车的速度是千米／时。

【自学检测】（先用线段图分析等量关系，再列方程解答）甲、乙骑自行车同时从相距 65千米的两地相向而行，2小时相遇。

甲比乙每小时多骑2.5千米，求甲、乙的速度各是多少？线段图：等量关系：解：设二、展、导环节1、小明和小华从甲、乙两地同时出发，相向而行。

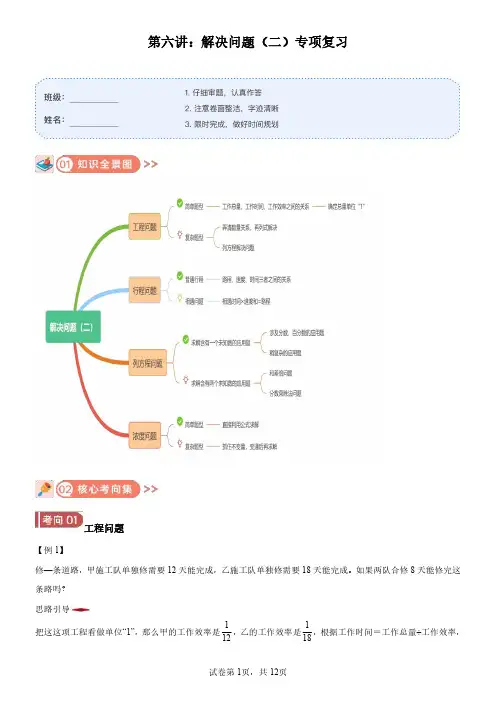
第六讲：解决问题（二）专项复习工程问题【例1】修—条道路，甲施工队单独修需要12天能完成，乙施工队单独修需要18天能完成。

如果两队合修8天能修完这条路吗？思路引导把这这项工程看做单位“1”，那么甲的工作效率是112，乙的工作效率是118，根据工作时间＝工作总量÷工作效率，求出甲乙两队合修需要的天数即可解答。

正确解答：1÷（112＋118）＝1÷（336＋236）＝1÷5 36＝36 5＝7.2（天）答：如果两队合修8天能修完这条路。

此题主要考查工作时间、工作效率、工作总量三者之间的数量关系，解答时往往把工作总量看做1，再利用它们的数量关系解答。

【变式1】1．一批货物，甲车单独运要10天运完，乙车单独运要15天运完。

甲、乙两车合运3天能运完整批货物的12吗？【例2】王阿姨编一个花篮，由原来的5分钟减少到4分钟，她的工作效率提高了百分之几？思路引导把编一个花篮的工作总量设为1，原来的工作时间是5分钟，那么原来的工作效率就是15；后来的工作时间是4分钟，那么后来的工作效率就是14；用（14－15）的差除以15，再将商化成百分数即可。

正确解答：（14－15）÷15＝（520－420）÷15＝120÷15＝1 4＝25%答：她的工作效率提高了25%。

解决本题先把工作总量设为1，分别表示出原来和现在的工作效率，再根据求一个数是另一个数百分之几的方法求解。

【变式2】2．一项工程，师傅用12小时可完成，徒弟用16小时可完成。

师傅的效率比徒弟快（）。

A．75%B．33.3%C．25%D．133.3%行程问题【例3】甲、乙两车同时从两地相向而行，半小时相遇。

已知两地相距90千米，甲乙两车速度比是5∶4，求甲乙两车的速度？思路引导根据公式：速度和＝两地距离÷相遇时间，用90除以0.5，即可求出两车的速度和，再按照5∶4进行分配即可据此解答。

小学六年级方程知识点总结方程是数学中的重要概念，在小学六年级的学习中，我们也开始接触和学习一元一次方程。

方程是一个数学等式，在方程中，我们用字母表示未知数，通过运算求出未知数的值。

接下来，让我们来总结一下小学六年级方程的主要知识点。

一、方程的基本概念方程是由等号连接的两个代数式，其中含有未知数。

在一元一次方程中，我们只有一个未知数。

例如：3x + 2 = 8，其中的 x 就是未知数。

二、方程的解在方程中，我们需要找到使等式成立的未知数的值，这个值就是方程的解。

对于一元一次方程，我们通常使用逆运算的方法求解。

例如：对于方程 3x + 2 = 8，我们可以先减去2，再除以3，得到 x = 2。

三、方程的解的判断在解方程的过程中，我们需要验证求得的解是否符合原始方程。

将求得的解代入方程中，如果等式仍然成立，则我们找到了方程的解；如果等式不成立，则需要重新检查求解步骤。

四、用方程解决问题方程可以帮助我们解决很多实际问题。

在解决问题时，我们需要先列出方程，然后通过求解方程找到问题的答案。

例如：小明年龄的三分之一比小红年龄少4岁，如果小明的年龄是 x，那么我们可以列出方程：(1/3)x = x - 4，通过求解这个方程，我们可以得到小明的年龄。

五、方程的应用方程在日常生活中有着广泛的应用。

除了用于解决问题外，方程还可以用来描述自然界中的现象规律，例如牛顿第二定律 F = ma，也是一个方程。

方程还可以用于经济学、物理学、化学等各个领域的研究中。

六、常见的方程错误在解方程的过程中，有些常见的错误需要我们注意避免。

例如，漏解方程中的负数解、在计算过程中的运算错误、代入验证时的计算错误等。

我们在解方程时，要仔细思考每一步的计算和验证，避免这些错误的出现。

通过本文的总结，我们了解了小学六年级方程的主要知识点。

方程作为数学的重要内容，不仅在学习中有着重要的作用，也广泛应用于各个领域。

在今后的学习和实践中，我们要继续加深对方程的理解，提高解方程的能力，更好地应用方程解决实际问题。

列方程解决问题知识点总结一、基本概念1.1 列方程解决问题的定义列方程解决问题是指在实际问题中，根据已知条件，将问题中的未知量用代数式表示出来，并根据代数式进行推理推导，最终得出未知量的值的过程。

列方程解决问题是数学中一个重要的解决问题方法，应用广泛，对学生的思维能力和逻辑推理能力有很好的锻炼作用。

1.2 列方程解决问题的要素在列方程解决问题的过程中，有一些重要的要素需要注意。

首先，需要明确问题中的未知量，例如长度、面积、体积等；其次，需要从已知条件中提取信息，并将其转化为已知量和关系；最后，需要通过列方程，利用代数式进行推理推导，最终得出未知量的值。

1.3 列方程解决问题的意义列方程解决问题是数学中的一个基本技能，掌握了这一技能，可以帮助学生更好地理解和应用代数知识。

同时，列方程解决问题也是一种思维能力的锻炼，有助于培养学生的逻辑推理能力和问题解决能力。

二、步骤2.1 理解问题在列方程解决问题的过程中，首先需要理解问题，明确问题要求和已知条件，找出问题中的未知量，并确定问题中的关键信息。

2.2 建立代数式根据问题中的已知条件，将未知量用代数式表示出来，并建立方程。

在建立代数式的过程中，需要注意运用代数知识，适当引入变量，并确保代数式与实际问题一一对应。

2.3 求解方程根据建立的代数方程，可以通过解方程的方法，求出未知量的值。

解方程的方法有代数法、图形法、数学归纳法等，根据问题的不同可以选择不同的方法。

2.4 验证答案在求出未知量的值后，需要将其代入到原方程中进行验证，确保所得的解是正确的。

如果验证结果正确，则说明所得的解是正确的；如果验证结果错误，则需要重新考虑解决问题的过程。

2.5 综合评价对于一些复杂的问题，可能需要综合考虑不同的条件和方法，对解题的过程和结果进行综合评价，确保解题的准确性和完整性。

三、实际应用3.1 长方形的面积问题假设一个长方形的长是x，宽是x-4，已知它的面积是24。

一方程1、列方程解决实际问题（一）改错：5x-40=20解：5x÷5-40=20÷5 改正：x-40=4x=44列方程解下面各题。

1.在2010年广州亚运会上，中国代表队获得奖牌416枚，比印度代表队获得奖牌数的7倍少32枚，印度代表队获得奖牌多少枚？2.2011年5月1日，王华在故宫晚时拍了35张相片，比他在颐和园游玩拍的照片的2倍多9张。

他在颐和园游玩拍了多少张相片？先写出题中等量关系，再列方程。

1.爸爸今年45岁，比冬冬年级的2倍还多9岁，冬冬今年x 岁。

等量关系：方程：2.码头有32吨货物，用载重量为x吨的汽车运了6次后，还剩5吨。

等量关系：方程：把计算错误的地方改正过来。

改正改正2011年西安世界园艺博览会园区占地面积是418公顷，是园区中水域面积的3倍少146公顷，园区中水域面积是多少公顷？杭州湾跨海大桥是世界最长的跨海大桥。

桥上两座三角形主塔的高都是187米，每座主塔正面的面积是3085.5平方米，那么桥面宽多少千米？广州平安路小学六年级三班的全体同学参加义务植树。

如果每人种6棵数，那么剩余15棵树苗；如果每人种7棵树，那么少30棵树苗，这个班有多少名学生？下面是2011年1月份日历，现用一个长方形框在日历框出4个数，若框出的4个数之和恰好是100，则框出的第一个数应是几？5个相邻整数之和是135，那么最小的数是（）。

2、列方程解决实际问题（二）小明和小红去图书馆借书，他们借的故事书是科技书的3倍，如果再借16本科技书，两种书的本数就一样多。

故事书和科技书各借多少本？距140千米，A车的速度为80千米/时，B车的速度为60千米/？”你能帮助小明补充一个数学问题，并解答出来吗？泰国热带丛林里的小飞鼠是世界上最小的哺乳动物。

一只麻雀的体重是它的53倍。

一只小飞鼠比一只麻雀轻104克，你知道它们的题中分别是多少吗？唐僧师徒四人去西天取经，一日傍晚，路过一座院子，院内有宝塔一座，宝塔层层都是红灯，唐僧师徒正想进院数红灯，不料被一和尚堵住去路他念了一首诗：远望巍巍塔七层，红灯点点倍加增，共计三百八十一，试问顶层几盏灯。