考研数学一、数学三模拟试题

全国硕士研究生入学统一考试数学(三)考前模拟卷1.【单项选择题】A. k≠1B. k>1C. k>0D. 与k无关正确答案：A参考解析：2.【单项选择题】A. 极限不存在．B. 极限存在，但不连续．C. 连续，但不可导．D. 可导．正确答案：C参考解析：先分别考察左、右可导性．3.【单项选择题】当x→0时下列无穷小中阶数最高的是A.B.C.D.正确答案：C参考解析：(A)(考察等价无穷小) 4.【单项选择题】A.B.C.D.正确答案：D参考解析：5.【单项选择题】设A是m×n阶矩阵，则下列命题正确的是( )．A. 若m<n，则方程组AX=b一定有无穷多个解B. 若m>n，则方程组AX=b一定有唯一解C. 若r(A)=n，则方程组AX=b一定有唯一解D. 若r(A)=m，则方程组AX=b一定有解正确答案：D参考解析：6.【单项选择题】A. 1，0，-2．B. 1，1，-3．C. 3，0，-2．D. 2，0，-3．正确答案：D参考解析：7.【单项选择题】二次型f(x1，x2，x3)=(x1-x2)2+(x2-x3)2+(x3-x1)2的标准形为( ).A. f=B. f=2C. f=D. f=2正确答案：B参考解析：用配方法，8.【单项选择题】设随机变量X～U[0，2]，Y=X2，则X，Y( )．A. 相关且相互独立B. 不相互独立但不相关C. 不相关且相互独立D. 相关但不相互独立正确答案：B参考解析：【解】9.【单项选择题】A.B.C.D.正确答案：D参考解析：10.【单项选择题】A.B.C. 0D.正确答案：B 参考解析：11.【填空题】正确答案：参考解析：【解析】12.【填空题】正确答案：参考解析：1【解析】13.【填空题】正确答案：参考解析：【解析】14.【填空题】正确答案：参考解析：【解析】15.【填空题】正确答案：参考解析：6【解析】若按第1行展开，只有-2x乘以其代数余子式会出现x3项，故只要求出这一项即可．故x3的系数为6．16.【填空题】设X，y为两个随机变量，且D(X)=9，Y=2X+3，则X，Y的相关系数为________正确答案：参考解析：1【解析】D(Y)=4D(X)=36，17.【解答题】参考解析：18.【解答题】求函数z=x3-3x2-3y2在闭区域D：x2+y2≤16上的最大值．参考解析：解(Ⅰ)得驻点(0，0)，(2，0)．(Ⅱ)在D：x2+y2=16上．得(0，±4)．(±4，0)．(Ⅲ)比较大小z(0，0)=0，z(2，0)=-4，z(0，4)=-48，z(0，-4)=-48，z(4．0)=16，z(-4，0)=-112，得最大值为z(4，0)=16．19.【解答题】参考解析：20.【解答题】参考解析：【解】21.【解答题】α1=(1，1，0)T，α2=(0，2，1)T．(Ⅰ)求A的特征值与特征向量；(Ⅱ)求可逆矩阵P，使得P-1AP=Λ．参考解析：解(Ⅰ)由A～B知，A与B有相同的特征值，而由|μE一B|=0，可得B的特征(Ⅱ)22.【解答题】设随机变量X1，X2，X3相互独立，且均服从参数为λ的指数分布，记Y=min{X1，X2)，T=max{Y，X3}．(Ⅰ)求y的概率密度f Y(y)；(Ⅱ)求期望ET．参考解析：解(Ⅰ)由已知，X1与X2相互独立，故(X1，X2)的概率密度为(II)先求T的分布函数与概率密度．。

数学一考研模拟试题及答案一、选择题（每题4分，共40分）1. 下列函数中，满足f(-x) = f(x)的是（）A. f(x) = x^2B. f(x) = |x|C. f(x) = x^3D. f(x) = sin(x)2. 设函数f(x)在点x=a处连续，且lim (x→a) [f(x) - f(a)]/(x-a) = L，那么f'(a) = （）A. LB. 0C. 不存在D. 13. 曲线y = x^2 在点(1,1)处的切线斜率为（）A. 1B. 2C. 4D. 04. 设随机变量X服从参数为λ的泊松分布，P(X=k) = e^(-λ) *λ^k / k!，k=0,1,2,...，则E(X)等于（）A. λB. λ^2C. kD. e^λ5. 以下哪个数列是发散的？（）A. 1, 1/2, 1/3, ...B. 1, 2, 4, 8, ...C. 1, 0, 1, 0, ...D. -1, 1, -1, 1, ...6. 设A和B是两个n阶方阵，|A| = 2，|B| = 3，则|AB| = （）A. 6B. 5C. 1D. 无法确定7. 以下哪个选项是正确的？（）A. ∫(0 to 1) x^2 dx = 1/3B. ∫(0 to 1) x^2 dx = 1/2C. ∫(0 to 1) x^2 dx = 2/3D. ∫(0 to 1) x^2 dx = 3/28. 设函数f(x)在区间[a,b]上可积，且f(x) ≥ 0，则（）A. ∫(a to b) f(x) dx ≥ 0B. ∫(a to b) f(x) dx > 0C. ∫(a to b) f(x) dx = 0D. 无法确定9. 以下哪个级数是收敛的？（）A. 1 + 1/2 + 1/3 + ...B. 1 - 1/2 + 1/2 - 1/3 + ...C. 1 + 1/4 + 1/9 + ...D. 1 - 1/2 + 1/4 - 1/8 + ...10. 设函数f(x)在点x=a处可导，且f'(a) = 2，则曲线y = f(x)在点(x=a, y=f(a))处的切线方程为（）A. y = 2x - aB. y = 2x - 2aC. y = 2x + f(a)D. y = 2x - f(a)/2二、填空题（每题4分，共20分）11. 若函数f(x) = 2x^3 - 3x^2 + 5在点x=1处取得极小值，则f'(1) = ____。

2022年全国硕士研究生入学统一考试（数学三）模拟试卷一解答一、选择题：1～10小题，每小题5分，共50分．下列每题给出的四个选项中，只有一个选项是符合要求的．请将所选项前的字母填在答题纸指定位置上．（1）答案：选（D）.解由()0lim[1]0f x x e →-=，有0lim ()0(0)x f x f →==，故22()000ln(1)lim lim lim 1()(0)1()f x x x x x x x f x f e f x x→→→+===--，可得0()(0)(0)lim 0x f x f f x→-'==.又因20lim 10()x x f x →=>，由保号性知,在 (0)U内，()0(0)f x f >=，从而()f x 在0x =处取极小值(0)0f =.选（D）.（2）答案:选(D).解由题设极限可知(0,0)0,(0,0)2,(0,0)1x y f f f ''===，且函数在(0,0)点可微.()22221ln(1(1cos ,1))sin sin 0lim 1(1cos ,1)lim x f x e x xxx x f x e e+--→→+--=，222200ln(1(1cos ,1))(1cos ,1)limlimsin x x x x f x e f x e x x →→+----=0x →=2222001(0,0)(0,0)2lim lim 112,x y x x f x f x x x→→'⋅'⋅=+=+=所以原极限，故选(D).（3）答案:选（B）.解224222004cos sin cos sin cos sin 111x x x x x x I J dx dx dx x x x ππππ----==++++⎰⎰⎰.对后一个积分，令2x t π=-，得024202244cos sin sin cos sin cos (11()1()22x x t t x x dx dt dx x t x ππππππ---=-=++-+-⎰⎰⎰），故42211(cos sin )[]011()2I J x x dx xx ππ-=-->++-⎰，即I J >.故选（B）.（4）答案:选(C).解原极限211221lim(n nn i j i j f n n n n →∞===+⋅∑∑，令2ix n=，当:1()i n n →→∞时，:02x →，令jy n=，当:12()j n n →→∞时，:02y →，所以区域为{(,)|02,02}D x y x y =≤≤≤≤，因此原极限22()dx f x y dy =+⎰⎰.故选(C).（5）答案：选（Ｄ）.解法1因为220()(())()A bA cE A kE A k E k E b bk c ++=⇒-+=-+++，若矩阵A 对任何实数k ，A kE -可逆，需20k bk c ≠++.欲对任何实数k ,20k bk c ≠++,即方程20k bk c =++无实数解,故,b c 需满足204b c <-.所以（Ｄ）正确.解法2A kE -可逆k ⇔不是A 的特征值20k bk c ⇔++=无实数解20.4⇔<-b c 故选（Ｄ）.（6）答案：选（B）.解由题设10,0A A x β==知有非零解，故()2r A ≤，又()()r AB r A <，从而()1r AB ≤；由20,A β≠2β不是方程组0Ax =的解，即AB O ≠，故()1r AB ≥.综上得()1r AB =，故选（B ）.（7）答案：选（B ）.解由()r A m =知A 一定可以只经过一系列的初等列变换化为(),,m E O ①不正确；由()r A m =知(,)r A b m =，则Ax b =有解，但无法判定是无穷多解还是有唯一解，故②不正确；m 阶方阵B 满足BA O =⇒()()r B r A m +≤，且知()r A m =()0r B B O ⇒=⇔=，故③正确；TAA 为m 阶方阵，又()()T r A r A m ==，则知0T A x = 仅有零解，即对0,()()0T T T T T T x x AA x A x A x AA ∀≠=>⇒为正定矩阵.④正确．选（B ）.（8）答案：选（C ）.解设A 表示6次射击恰好命中4次；B 表示4次射击恰好命中3次；2313244262121()()()()()23333()21()5()()33C C P AB P B A P A C ===，故选（C ）.（9）答案:选（C）.解22222222ˆˆˆ()()[()]E D E σσσσσσ-=-+-2222ˆˆ(),D E σσσ=+-222211ˆˆn n S E n nσσσ--=⇒=,()()22422422211222ˆ()1n n n D D S n n n n σσσ---==⋅=-故22244422222121ˆ()n n E n n nσσσσσ---=+=22244422222121ˆ()n n E n n nσσσσσ---=+=故选（C）.（10）答案：选（A ）.解由0{0}1{1}2{2}EX P X P X P X =⋅=+⋅=+⋅=2{1}2(1)2(1)P X θθ==+-=-得{1}2(1)P X θθ==-,故2{0}.P X θ==22244()[2(1)](1)4(1)L θθθθθθθ=⋅--=-，ln ()ln 44ln 4ln(1)L θθθ=++-ln ()4401d L d θθθθ=-=-解得1ˆ2θ=，故选（A ）.二、填空题:11～16小题，每小题5分，共30分．请将答案写在答题纸指定位置上．(11)答案：填20212-．解21cos 2121()(12)cos (12)cos 2cos 2222x x f x x x x x x x ++=+=+⋅=++,()(cos 2)=2cos(2)2n n n x x π+,于是(2022)2021(0)2f =-．(12)答案：填()22112ln 44f x x x e =--．解设1()x f e dx A =⎰，由题设，有120()2()x x x f e xe f e dx =-⎰.两边积分，得1202x A xe dx A =-⎰,则11221222120000111112[][][1]22224xx x x A xe dx xe e dx e e e ==-=-=+⎰⎰.故()22112ln 44f x x x e =--.（13）答案：填32sin 44(cos ,sin )d f r r rdr πθπθθθ⎰⎰.(14)答案：填2k <.解由于x →+∞时，333113(1)x x x e ee e e x +-=- ，原积分与331111kkx dx dx x x +∞+∞-⋅=⎰⎰的敛散性相同，312k k ⇒->⇒<.（15）答案：填2-..解由合同矩阵所对应的二次型具有相同的规范形，于是B 的正、负惯性指数均为1，()112r B =+=.则2(1)(2)01B a a a =--+=⇒=或2a =-.若1a =，则()1r B =不合题意；若2a =-，由0B E B λ-=⇒的特征值为0,3,3-，此时B 的正、负惯性指数均为12a ⇒=-.（16）答案：填23e .解由题意，()11(1)10,f ae a b e--'=-+=故得0b =又00()1,x f x dx axe dx a +∞+∞-===⎰⎰20()2x EX x f x dx x e dx +∞+∞-=⋅==⎰⎰.223{}{2}.x P X EX P X xe dx e+∞-≥=≥==⎰三、解答题:17～22小题，共70分．请将解答写在答题纸指定位置上．解答应写出文字说明、证明过程或演算步骤．(17)解由题意,点P 处的切线方程为()()()Y f x f x X x '-=-,令0Y =,解得()()f x u x f x =-'.2000()()lim lim[1]1lim ()()→→→=-=-''x x x f x u f x x f x x xf x x其中2000()()()(0)1limlim lim (0),222→→→'''-''===x x x f x f x f x f f x x x 0()lim (0)x f x f x →'''=,故01lim .2→=x u x 220022(0)(0)(0)()()2!lim lim (0)()(0)(0)()2!x x f f f u u o u f u f f x f f x x o x →→'''+++='''+++2220022(0)()12lim lim().(0)4()2→→''+===''+x x f u o u u f x x o x （18）解由对称性可知，区域D 关于x3y为奇函数，所以30D=.再由对称性可知，123212022D I d πθ==⎰⎰⎰2232012(sin cos sin cos )4d πθθθθθ=⋅-⎰332220011sin (cos (1cos ))23d ππθθθθ⎡⎤=--⎢⎥⎣⎦⎰1124212335310⎡⎤⎛⎫=--⋅= ⎪⎢⎥⎝⎭⎣⎦.或123212022D I d rdrπθ==⎰⎰⎰2245222000111112(1cos )sin cos sin sin sin .422510πππθθθθθθθ=⋅-==⋅=⎰⎰d d （19）解(Ⅰ)因为00a =，11a =，设1k a ≤，则1112133k k k a a a +-=+≤，由归纳法可知1n a ≤.又因为1!!n n n a x x n n ≤，且级数01!n n x n ∞=∑的收敛域为(),-∞+∞，由比较判别法知，0!n n n a x n ∞=∑的收敛域也为(),-∞+∞.(Ⅱ)0()!n n n a s x x n ∞==∑，所以1110()(1)!!n n n n n n a a s x x x n n ∞∞-+=='==-∑∑，2220().(2)!!n n n n n n a a s x x x n n ∞∞-+==''==-∑∑因为211233n n n a a a ++=+，故21100002112()2()()!3!3!!33n n n n n n n n n n n n n a a a a a s x x x x x s x s x n n n n ∞∞∞∞+++====+⎛⎫'''===+=+ ⎪⋅⎝⎭∑∑∑∑，因此和函数满足的微分方程为12()()()033s x s x s x '''--=.(Ⅲ)设特征方程为212033r r --=，则方程的根分别为1221,3r r ==-，故二阶微分方程的通解为2312()x xs x c e c e-=+，代入01(0)0,(0)1s a s a '====，可得135c =，235c =-，从而2333()55x x s x e e-=-.(20)解(I)(,)P x y 点的切线方程为()(,0)yY y y X x T x y '-=-⇒-'.由222222(()y y xyPT OT y x y y y x y '=⇒+=-⇒=''-，即221()y x y y x '=-.令y u x=,则有222221211(1)du u u u u x du dx dx u u u x +-+⋅=⇒=-+⎰⎰22221lnln ln 11u u x C Cx x y y u u C⇒=+⇒=⇒+=++.把(1,1)代入得12C =，故曲线方程为222x y y +=.（II）221111(1(1V dx dxππ--=-⎰⎰1214=πππ-==⎰⎰（21）解（Ⅰ）由于(2)0A E x -=的基础解系中含3个线性无关的解向量，则12λ=至少是A 的3重特征值，再由41()i i tr A λ==∑得A 的另一个特征值为24λ=-；则A 有4个线性无关的特征向量，故A 可对角化，即A 可相似于一个对角阵.（Ⅱ）由于12λ=是A 的3重特征值，故有212324313234414243(2)102222,22r A E r a a a a a a a a a -==-⎛⎫ ⎪- ⎪⎪- ⎪-⎝⎭进而解得2131412434424323320,2,2a a a a a a a a a =========-，于是2222002202020220A -⎛⎫ ⎪-⎪= ⎪- ⎪⎝⎭.注意到1234(,,,)T T f x x x x x Ax x Bx ==，其中21111022=120221220T A A B -⎛⎫⎪-+ ⎪=⎪- ⎪-⎝⎭，B的特征值为123,42,1λλλ===-±当122a =时，则1234(,,,)f x x x x在正交变换下的标准形为2222123422(1(1f y y y y =++-++--.（22）解(Ⅰ){1,}=1,arctan }44Y P U V P X ππ≤≤≤≤1400211==2r d e rdr eπθπ--⎰⎰．(Ⅱ)记(,)U V 的分布函数为,(,)U V F u v ，则,(,){,}U V F u v P U u V v =≤≤．①当0u <或0v <时，,(,)0U V F u v =；②当0,02u v π≥≤≤时，,(,){,}=,arctan}U V Y F u v P U u V v P u v X=≤≤≤22==(1(1))v ur u vd e rdr u e θππ---+⎰⎰；③当0,2u v π≥≥时，,(,){,}=,arctan}2U V Y F u v P U u V v P u X π=≤≤≤≤202==1(1)uru d e rdr u e πθπ---+⎰⎰进而得2,,2(,),0,0,(,)20,.uU V U V F u v ue u v f u v u vππ-⎧∂≥≤≤⎪==⎨∂∂⎪⎩其它(Ⅲ)U 和V 的边缘密度分别为20,2,0,,0,()(,)0,,0,uu U U V ue u ue dv u f u f u v dv ππ--+∞-∞⎧⎧≥≥⎪===⎨⎨⎩⎪⎩⎰⎰其它其它+0,22,0,,0,()(,)220,0,,uV U V ue du v v f v f u v du ππππ∞-+∞-∞⎧⎧≤≤≤≤⎪⎪===⎨⎨⎪⎪⎩⎩⎰⎰其它其它由于,(,)()()U V U V f u v f u f v =，所以U 和V 相互独立．。

考研数学三模试题及答案一、选择题（每题3分，共36分）1. 下列函数中，满足条件f(-x) + f(x) = 0的是：A. f(x) = x^2B. f(x) = |x|C. f(x) = sin(x)D. f(x) = e^x2. 已知函数f(x)在区间(a, b)内可导，且f'(x) > 0，则f(x)在该区间内：A. 单调递增B. 单调递减C. 常数函数D. 无单调性3. 设曲线C：y^2 = 4x与直线l：x = 2 + t，y = 3 - 2t相切，则实数t的值为：A. 1B. 2C. 3D. 44. 已知函数f(x) = 2x - 3，g(x) = x^2 + 1，若f[g(x)] = 9x^2 - 6x，则x的取值范围是：A. x > 1B. x < 1C. x > 0D. x < 05-10. （略，类似结构）二、填空题（每题4分，共24分）11. 若函数f(x) = √x在区间[0, 4]上的最大值为M，则M的值为________。

12. 设等比数列{an}的首项为1，公比为2，其前n项和为S_n，则S_5的值为________。

13. 若矩阵A = [1, 2; 3, 4]，则|A| =________。

14. 设双曲线x^2/a^2 - y^2/b^2 = 1的离心率为2，且过点(1, √3)，则a的值为________。

15-16. （略，类似结构）三、解答题（共40分）17. （12分）设函数f(x)在区间[a, b]上连续，且∫[a, b] f(x) dx = 3，证明对于任意的m，n ∈ [a, b]，都有∫[a, b] f(x) dx ≥(1/(b-a)) * (m - n)^2。

18. （14分）已知某工厂生产商品x件的总成本为C(x) = 2000 +50x，销售每件商品的收入为p(x) = 110x - x^2，求该工厂的月利润最大值。

考研数学三真题模拟试卷本试卷共分为两个部分，第一部分为选择题，第二部分为解答题。

请考生按照要求完成答题，并将答案写在答题卡上。

第一部分选择题（共40题，每题4分，共160分）在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项的答案填写在答题卡上。

1. 设f(x) = 2e^x，g(x) = x^2，则f(g(x))的导数为：A. 2xe^xB. 4e^xC. e^xD. 2x^2e^(x^2)2. 已知函数f(x)满足f'(x) = 2x^3 - 3x^2 - 12x，且f(2) = 4，则f(x)的表达式为：A. x^4 - x^3 - 6x^2 + 4B. x^4 - 2x^3 - 6x^2 + 4C. x^4 - x^3 - 6x^2 + 8D. x^4 - 2x^3 - 6x^2 + 83. 已知三个点A(-2, 3)，B(4, -1)和C(x, 2)，若点C在直线AB上，则点C的坐标为：A. (3, 2)B. (-1, 2)C. (-4, 2)D. (0, 2)4. 设函数f(x) = x^3 - 4x^2 + mx - 4，其中m为实数。

若函数f(x)的值域为[-4, 4]，则m的取值范围是：A. [-2, 2]B. [-4, 4]C. [-5, 5]D. [-6, 6]......（省略其余题目）第二部分解答题请将解答题的详细过程和答案写在答题卡上。

1. 求函数f(x) = x^3 - 6x^2 + 11x - 6的极值点及其类型。

解答：首先，求导得f'(x) = 3x^2 - 12x + 11，令f'(x) = 0，解得x = 2和x = 1/3。

然后，求二阶导数得f''(x) = 6x - 12。

当x = 2时，f''(x) = 0，代入到f(x)中得f(2) = -1。

当x = 1/3时，f''(x) > 0，代入到f(x)中得f(1/3) = 26/27。

考研数学（数学三）模拟试卷400(题后含答案及解析) 题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．设f(x)满足f”(x)+x[f’(x)]2—sin x，且f’(0)=0，则( )A．f(0)是f(x)的极小值．B．x(0)是f(x)的极大值．C．在点(0，f(0))左侧邻域内，曲线y=f(x)是凹的，右侧邻域内，曲线y=f(x)是凸的．D．在点(0，f(0))左侧邻域内，曲线y=f(x)是凸的，右侧邻域内，曲线y=f(x)是凹的．正确答案：D解析：由f”(x)+x[f’(x)]2=sin x，有f”(0)=0．再由f”‘(x)+[f’(x)]2+2xf’(x)f”(x)=cos x，得f”‘(0)=1，所以=1。

由极限的保号性知，存在x=0的去心邻域且x＞0时，f”(x)＞0．故应选(D)．2．设f(x)在区间(—∞，+∞)上连续，且满足f(x)=∫0xf(x—t)sin tdt+x，则在(一∞，+∞)上，当x≠0时，f(x) ( )A．恒为正．B．恒为负．C．与x同号．D．与x异号．正确答案：C解析：作积分变量代换，令x—t=u，得f(x)=∫x0f(u)sin(x—u)d(一u)+x=∫0xf(u)sin(x一u)du+x =sin x．∫0xf(u)cos udu一cos x．∫0xf(u)sin udu+x，f’(x)=cos x．∫0xf(u)cos udu+sin x．cos x．f(x)+sin x．∫0xf(u)sin udu一cos x．sin x．f(x)+1 =cos x．∫0xf(u)cos udu+sin x．∫0xf(u)sin udu+1，f”(x)=—sin x．∫0xf(u)cos udu+cosx．f(x)+cos2x．∫0xf(u)sin udu+sin2x．f(x) =f(x)一f(x)+x=x．3．设f(x)=一sinπx+(3x—1)2，则在区间(一∞，+∞)上，f(x)的零点个数( )A．正好1个．B．正好2个．C．正好3个．D．多于3个．正确答案：B解析：f(0)=1＞0，＜0，f(1)=4＞0，所以至少有2个零点．又f’(x)=一πcos πx+6(3x一1)，f”(x)=π2sin πx+18＞0，所以至多有2个零点，故正好有2个零点．4．设f(x)=x4sin+xcosx(x≠0)，且当x=0时，f(x)连续，则( )A．f”(0)=0，f”(x)在x=0处不连续．B．f”(0)=0，f”(x)在x=0处连续．C．f”(0)=1，f”(x)在x=0处不连续．D．f”(0)=1，f”(x)在x=0处连续．正确答案：A解析：5．设A是n阶矩阵(n＞1)，满足Ak=2E，k＞2，E是单位矩阵，A*是A 的伴随矩阵，则(A*)k ( )A．E．B．2E．C．2k—1E．D．2n—1E．正确答案：D解析：Ak=2E，｜Ak｜=｜2E｜=2n，｜A｜=，得A*=｜A｜A—1，则(A*)k=(｜A｜A—1)k=｜A｜k(Ak)—1=｜A｜k(2E)—1=｜A｜kE=2n—1E，故应选(D)．6．设A是3阶矩阵，｜A｜=1，a11=一1，aij=Aij，其中Aij是A中元素aij的代数余子式，则线性非齐次方程组AX=的唯一解是( ) A．(1，0，0)T．B．(0，0，一1)T．C．(1，1，1)T．D．(一1，1，1)T．正确答案：A解析：将｜A｜按第1行展开，｜A｜=a11A11+a12A12+a13A13=a112+a122+a132，因｜A｜=1，a11=一1，故得a12=a13=A12=A13=0．故应选(A)．7．设(X，Y)为二维连续型随机变量，则下列公式各项都有意义的条件下(Df(x，y)=fX(x)Y(x)；②fX(x)=∫—∞+∞fY(y)fX|Y(x｜y)dx；③fX｜Y(x｜y)=；④P{X＜Y)=∫—∞+∞fX(y)fY(y)dy，其中FX(y)=∫—∞yfX(x)dx．必定成立的个数为( )A．1．B．2．C．3．D．4．正确答案：A解析：①需要独立条件才成立；②应该为fX(x)=∫—∞+∞f(x，y)dy=∫—∞+∞fY(y)fX|Y(x｜y)dy；③fX|Y(x｜y)成立；④需要独立条件．8．设随机变量X服从参数为1的指数分布，令Y=max{X，1}，则EY= ( ) A．1．B．1+．C．1一．D．．正确答案：B解析：填空题9．设f(x)=，则f[f(x)]=_________．正确答案：解析：由f(x)的表达式，有最后，分别写出自变量的取值范围，易见第4式中＞1与x＞1的交集为空集，故化简为如答案所示。

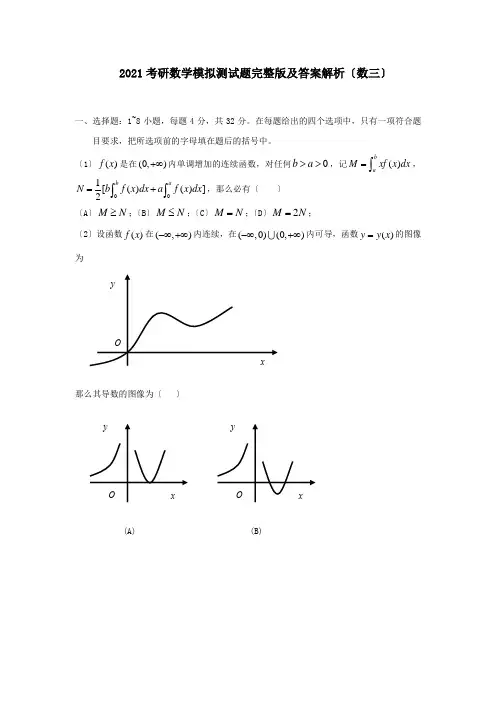
2021考研数学模拟测试题完整版及答案解析〔数三〕一、选择题：1~8小题，每题4分，共32分。

在每题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号中。

〔1〕()f x 是在(0,)+∞内单调增加的连续函数，对任何0b a >>，记()baM xf x dx =⎰，01[()()]2b a N b f x dx a f x dx =+⎰⎰，那么必有〔 〕〔A 〕M N ≥；〔B 〕M N ≤；〔C 〕M N =；〔D 〕2M N =； 〔2〕设函数()f x 在(,)-∞+∞内连续，在(,0)(0,)-∞+∞内可导，函数()y y x =的图像为那么其导数的图像为〔 〕(A) (B)y xOyxOxyO(C) (D)(3)设有以下命题： ①假设2121()n n n uu ∞-=+∑收敛，那么1n n u ∞=∑收敛； ②假设1n n u ∞=∑收敛，那么10001n n u ∞+=∑收敛；③假设1lim1n n n u u +→∞>，那么1n n u ∞=∑发散； ④假设1()n n n u v ∞=+∑收敛，那么1n n u ∞=∑，1nn v∞=∑收敛正确的选项是〔 〕〔A 〕①②〔B 〕②③〔C 〕③④〔D 〕①④(4)设220ln(1)()lim 2x x ax bx x→+-+=，那么〔 〕 〔A 〕51,2a b ==-；〔B 〕0,2a b ==-；〔C 〕50,2a b ==-；〔D 〕1,2a b ==- (5)设A 是n 阶矩阵，齐次线性方程组〔I 〕0Ax =有非零解，那么非齐次线性方程组〔II 〕T A x b =，对任何12(,,)T n b b b b =〔A 〕不可能有唯一解； 〔B 〕必有无穷多解；〔C 〕无解； 〔D 〕可能有唯一解，也可能有无穷多解(6)设,A B 均是n 阶可逆矩阵，那么行列式1020TA B -⎡⎤-⎢⎥⎣⎦的值为 〔A 〕1(2)n A B--； 〔B 〕2T A B -； 〔C 〕12A B --； 〔D 〕12(2)n A B--(7)总体~(2,4)X N ，12,,,n X X X 为来自X 的样本，X 为样本均值，那么〔 〕y xOyxO〔A 〕2211()~(1)1n i i X X n n χ=---∑； 〔B 〕2211(2)~(1)1n i i X n n χ=---∑； 〔C 〕2212()~()2ni i X n χ=-∑； 〔D 〕221()~()2n i i X X n χ=-∑；(8)设随机变量,X Y 相互独立且均服从正态分布2(,)N μσ，假设概率1()2P aX bY μ-<=那么〔 〕 〔A 〕11,22a b ==；〔B 〕11,22a b ==-；〔C 〕11,22a b =-=；〔D 〕11,22a b =-=-； 二、填空题：9~14小题，每题4分，共24分。

考研数学（数学三）模拟试卷480(题后含答案及解析) 题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．设f(x)是(-∞，+∞)上连续的偶函数，且︱f(x)︱≤M当xε(-∞，+∞)时成立，则F(x)=是(-∞，+∞)上的( )。

A．无界偶函数B．有界偶函数C．无界奇函数D．有界奇函数正确答案：B解析：首先讨论F(x)的奇偶性，注意有可见F(x)是(-∞，+∞)上的偶函数，这样就可以排除答案C和答案D。

其次讨论F(x)的有界性，因F(x)是(-∞，+∞)上的偶函数，所以可限于讨论x≥0时F(x)的有界性，由于，由此可知，F(x)也是(-∞，+∞)上的有界函数，故应选B。

2．设f(x)=xex+1+，则f(x)在(-∞，+∞)内( )。

A．没有零点B．只有一个零点C．恰有两个零点D．恰有三个零点正确答案：C解析：求f’(x)，分析其单调性区间，由于f’(x)=ex+1(x+1)①＜0，x＜-1，②=0，x=-1，③＞0，x＞-1，因此x=-1是f(x)的最小值点，且f(-1)=，又，由连续函数的介值定理知，在(-∞，-1)与(-1，+∞)内必存在f(x)的零点，又因f(x)在(-∞，-1)与(-1，+∞)均单调，所以在每个区间上也只能有一个零点，因此，f(x)在(-∞，+∞)恰有两个零点，故应选C。

3．设f(x)是区间上的正值连续函数，且I=，K=，若把I，J，K按其积从小到大的次序排列起来，则正确的次序是( )。

A．I，J，KB．J，K，IC．K，I，JD．J，I，K正确答案：D解析：用换元法化为同一区间上的定积分比较大小，为此在中令arcsinx=t，由于，且dx=d(sint)=costdt，代入可得。

与此类似，在K=中令arctanx=t，由于，且dx=d(tant)=，代入可得。

由f(x)＞0且当时0＜cosx＜1，故在区间上f(x)cosx＜f(x)＜，从而积J＜I＜K，故应选D。

考研数学一模拟试题一、选择题（每题4分，共40分）1. 设函数f(x)在区间(a, b)内连续，且f(a) < 0，f(b) > 0，则根据零点定理可知：- A. 函数f(x)在(a, b)内必有零点- B. 函数f(x)在(a, b)内必有唯一的零点- C. 函数f(x)在(a, b)内可能没有零点- D. 函数f(x)在(a, b)内可能有一个或多个零点2. 已知函数g(x) = 3x^2 + 2x - 5，求其在x=1处的导数值：- A. 4- B. 6- C. 8- D. 103. 以下哪个选项是微分方程dy/dx + 3y = 6e^(3x)的通解？- A. y = 2e^(3x) - e^x + C- B. y = e^(-3x) + C- C. y = 2e^(3x) - 3e^x + C- D. y = e^(3x) + C二、填空题（每题5分，共20分）1. 若极限lim(x→∞) (x^2 - 1)/(x^3 + 2x) = L，则L的值为______。

2. 设随机变量X服从正态分布N(μ, σ^2)，若P(X ≤ μ + σ) =0.8413，求P(X ≤ μ)的值。

3. 已知曲线y = x^3 - 3x^2 + 2x在点(1, 0)处的切线方程为______。

三、解答题（共40分）1. （10分）证明：若函数f(x)在闭区间[a, b]上连续，在开区间(a,b)内可导，且f(a) = f(b) = 0，则至少存在一点c∈(a, b)，使得f'(c) = 0。

2. （15分）解微分方程：(x^2 - 1)y'' - 2xy' + 2y = 0。

3. （15分）设随机变量X和Y的联合密度函数为f(x, y) =(1/2)e^(-x - y)，其中x > 0，y > 0。

求：- (a) X和Y的边缘密度函数；- (b) X和Y的协方差。

考研数学（数学三）模拟试卷450(题后含答案及解析) 题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．已知当x→0时，f(x)=arcsinx－arctanax与g(x)=bx[x－ln(1+x)]是等价无穷小，则( )A．a=b=1。

B．a=1，b=2。

C．a=2，b=1。

D．a=b≠1。

正确答案：A解析：根据等价无穷小的定义，那么1－a=0，，则有a=1，b=1。

故选(A)。

2．设f(x)=+x，则f(x)有( )A．两条斜渐近线。

B．一条水平渐近线，一条斜渐近线。

C．两条水平渐近线。

D．一条斜渐近线，没有水平渐近线。

正确答案：B解析：函数f(x)无间断点，所以不存在垂直渐近线。

水平渐近线：在x→－∞方向，所以y=0为函数f(x)的一条水平渐近线。

斜渐近线：所以y=2x为函数f(x)的一条斜渐近线。

故选(B)。

3．设f(x)是连续且单调递增的奇函数，设F(x)=∫0x(2u－x)f(x－u)du，则F(x)是( )A．单调递增的奇函数。

B．单调递减的奇函数。

C．单调递增的偶函数。

D．单调递减的偶函数。

正确答案：B解析：令x－u=t，则F(x)=∫0x(x－2t)f(t)dt，F(－x)=∫0－x(－x－2t)f(t)dt，令t=－u，F(－x)=－∫0x(－x+2u)f(－u)du=∫0x(x－2u)f(－u)du。

因f(x)是奇函数，f(x)=－f(－x)，F(－x)=－∫0x(x－2u)f(u)du，则有F(x)=－F(－x)为奇函数。

F’(x)=∫0xf(t)dt－xf(x)，由积分中值定理可得∫0xf(t)dt=f(ξ)x，ξ介于0到x之间，F’(x)=f(ξ)x－xf(x)=[f(ξ)－f(x)]x，因为f(x)单调递增，当x＞0时，ξ∈[0，x]，f(ξ)－f(x)＜0，所以F’(x)＜0，F(x)单调递减；当x＜0时，ξ∈[x，0]，f(ξ)－f(x)＞0，所以F’(x)＜0，F(x)单调递减。

考研数学三模拟试题一、选择题（每题5分，共40分）1. 设函数\( f(x) = 2x^3 - 3x^2 + x - 5 \)，求\( f(-1) \)的值。

A. 7B. 9C. 11D. 132. 已知\( \lim_{x \to 0} \frac{\sin x}{x} = 1 \)，求\( \lim_{x \to 0} \frac{\sin 2x}{x} \)。

A. 1B. 2C. 4D. 83. 以下哪个选项不是正态分布的数学期望？A. \( \mu \)B. \( \sigma^2 \)C. \( \mu + 2\sigma \)D. \( 2\mu - 3\sigma \)4. 已知\( \int_{0}^{1} x^2 dx \)的值，求\( \int_{0}^{1} x^3dx \)的值。

A. \( \frac{1}{4} \)B. \( \frac{1}{3} \)C. \( \frac{1}{2} \)D. \( \frac{1}{5} \)5. 设随机变量\( X \)服从二项分布\( B(n, p) \)，求\( E(X) \)。

A. \( np \)B. \( nq \)C. \( 2np \)D. \( 2nq \)6. 以下哪个函数是周期函数？A. \( y = e^x \)B. \( y = \ln x \)C. \( y = \sin x \)D. \( y = x^2 \)7. 已知\( \frac{dy}{dx} = 3x^2 + 2x - 1 \)，求\( y \)的原函数。

A. \( y = x^3 + x^2 - x + C \)B. \( y = x^3 + 2x^2 - x + C \)C. \( y = x^3 + x^2 + 2x + C \)D. \( y = x^3 + 2x^2 - x + C \)8. 设矩阵\( A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \)，求矩阵\( A \)的特征值。

2022年全国硕士研究生入学统一考试（数学一）模拟试卷三解答一、选择题：1～10小题，每小题5分，共50分．下列每题给出的四个选项中，只有一个选项是符合要求的．请将所选项前的字母填在答题纸指定位置上．(1)答案：选（C）.解0x =为间断点.当0a =时，0,1x x ==均为可去间断点，不合题意.当0a ≠时，200lim ()lim ()0x x a f x f x b-+→→=-=.此时0x =为跳跃间断点.另外考虑可去间断点，11111111111limlimlim 11(1)x x x xx x x x e e e ee e x→→→----===----.即b e =-时，1x =为可去间断点，选（C）.（2）答案:应选(C).解由隐函数的求导法则，可知1(),1()1()z z z x y z y y z ϕϕϕ∂∂==''∂-∂-，()()1()u z f z f z x x y z ϕ'∂∂'=='∂∂-，()()()1()u z f z z f z y y y z ϕϕ'∂∂'=='∂∂-，所以()()()()()01()1()u u z f z z f z z x y y z y z ϕϕϕϕϕ''∂∂-=-=''∂∂--，故选(C).（3）答案：选（D）.解设()ln 1()10e x ef x x e x f x x e x x-'=--⇒=-=⇒= .x(,0)-∞0(0,)e e(,)e +∞()f x '+不存在-+()f x 单增不存在单减()1f e =-单增因为0lim (),lim (),lim (),()1x x x f x f x f x f e →-∞→→+∞=-∞=+∞=+∞=-，所以方程在(,0)-∞，(0,)e ，(,)e +∞内各有一个根，选（D）.（4）答案:选(D).解由奇偶对称性和轮换对称性可知，222222422422411d d ()d d 0()d d 22xy x y x y DD DI xe x y x y e x y x y e x y ------=++=++⎰⎰⎰⎰⎰⎰,222222224424222011()d d 4d ed 4de d x y r r D x y ex y er r r er r rππθθ----+==⋅⎰⎰⎰⎰⎰⎰22224224244131114e e d e (1)e e (5e 2)(25)22r rr r r e e ππππ----=⋅⋅=--=-+=-⎰，所以3(25)2I e π=-.（5）答案：选（B ）.解由()2r A =()()**1312r A n r A ⇒=⇒-=-=，则*0A x =的基础解系中含两个解向量，又由()2r A =⇒0A =*0A A A E A ⇒==⇒的列向量都是方程*0A x =的解向量，即*****1010,2,1,0,3,2,401010,(5,3,4)0,T T T T T A A a A a A A -==-=⇒-==（，，）（）（）（，，）且101,(5,3,4)TT-（，，）线性无关，则*0A x = 的通解为1212101534,,x k k k k =-+ T T（，，）（，，）为任意常数.选（B ）注若由()2r A =求出a ，即得矩阵,A 再求出*A ，最后解方程*0A x =，麻烦！（6）答案：选(B).解若C 的列向量组可由A 的列向量组线性表示，则c A C A O O B O B ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭ ，可得()()A C r r A r B O B ⎛⎫=+ ⎪⎝⎭；反之，令100100,,001001A B C ⎛⎫⎛⎫⎛⎫===⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，C 的列向量组不能由A 的列向量组线性表示，但()()A C r r A r B O B ⎛⎫=+⎪⎝⎭.（7）答案：选(C)．解（A ）不正确，反例：1111,1100A B ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭，21r r A B -−−−→．:2,0,:1,0A B λλ(B)不正确，反例：1000,0000A B ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭的行列式相等，但它们的秩不相等．（D ）不正确，反例：1120,1100A B ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭相似，但0Ax = 与0Bx =不同解．（C ）正确，0Ax =与0Bx =均只有零解说明二者秩均为n ，从而等价．（8）答案：选（A ）．解由题意(),(2p P B A p P B A ==，2(1)(),()2p p P AB p P AB -==，故2()2p p P B +=，23()()()()2p p P A B P A P B P AB -=+-= ．（9）答案：选（C ）．解由221X Y +=知（A ）、（B ）、（D ）不正确．由于201cos 02EX d πθθπ==⎰，201sin 02EY d πθθπ==⎰，201()cos sin 02E XY d πθθθπ==⎰，故()E XY EXEY =，所以X 与Y 不相关，（C ）正确．（10）答案：选（B ）．解由于100(),1,2,,!!ik k X ka a k k a E a a e e e e e i n k k λλλλλλλ∞∞---(-)==()=⋅==⋅==∑∑ ，故由11111111i in n n X X a a i i i E a E a e e e n n n λλλ(-)(-)===()=()===∑∑∑，解得2a =．二、填空题:11～16小题，每小题5分，共30分．请将答案写在答题纸指定位置上．(11)答案：填3222(1)2ππ++.解cos :sin x L y θθθθ=⎧⎨=⎩，()sin cos ()cos sin y y x θθθθθθθθ'+'=='-，23sin cos 12cos sin ()(cos sin )y x θθθθθθθθθθθ++⎛⎫''== ⎪'--⎝⎭，⇒2,2y y θπθπππ=='''==+，所以3322221(1)(1)2y R K y ππ'++===''+.（12）答案：填12.解记23sin (sin cos )xI dx x x π=+⎰,令2x t π=-，则222232200cos 111sec (sin cos )2(sin cos )2(tan 1)t x I dt dx dxt t x x x πππ===+++⎰⎰⎰220201(tan 1)1112(tan 1)2tan 12d x dx x x ππ+==-=++⎰.(13)答案.解(1,1,1)222(1,1,1)(){4,1,3}23i j kl rot A x y z yz x z xy ∂∂∂===-∂∂∂，0l =，222(1,1,1)(1,1,1)1+3ux xx y z ∂==∂+，由对称性可知(1,1,1)(1,1,1)13u uyz∂∂==∂∂.所以(1,1,1)111333u l∂=⋅⋅∂（14）答案：填4ln 3-.解令2222,y xP y Q x x y x y =+=---，则222221()P x y Q y x y x∂+∂=+=∂-∂，因此该积分在包含L ，且x y <的任意单连通区域内积分与路径无关，故取1:2,:11L y x =-→，则11211212111(2)d 4ln 4(ln ln 3)4ln 9422232L x x x x ---=+=+=+-=--+⎰⎰，或1121121211(2)d 4ln 4(ln ln 3)4ln 342223L x x x x ---=+=+=+-=--+⎰⎰.（15）答案：填1000210012100121⎛⎫⎪-⎪ ⎪-⎪-⎝⎭.解1[()]T T A E C B C E E ---=⇔[()]()T T A C B E E A C B E E --=⇔--=，则()1().TA CB E -=--因为1234012300120001C B E ⎛⎫ ⎪⎪--= ⎪⎪⎝⎭，10002100()32104321TC B E ⎛⎫⎪⎪--= ⎪⎪⎝⎭，则()110002100()12100121T A C B E -⎛⎫⎪- ⎪=--= ⎪-⎪-⎝⎭．（16）答案：填3a.解分别用X,Y 表示两点的坐标,则Z X Y =-,且2100,(,)~(,)()()0X Y x a y a X Y f x y f x f y a⎧≤≤≤≤⎪=⋅=⎨⎪⎩，其它.2013aaaEZ dx x ydx a =-=⎰⎰.三、解答题:17～22小题，共70分．请将解答写在答题纸指定位置上．解答应写出文字说明、证明过程或演算步骤．（17）解此二阶常系数非齐次线性方程得通解为33231212x x x y C e C xe x e =++.由(0)0,(0)0y y '==得120C C ==，故231()2x y x x e =.则tan ln(1)200023tan [(1)1](tan )1lim lim 2lim1()2xx x x x x e x x x xx e e x e e e y x x x e +→→→+-+--==200tan tan ln(1)22lim 2limx x x xx e e x x e→→+===.（18）解(Ⅰ)11(1)()11lim 11()1n n n x n x x x x n x +→∞-+-+=-++，令111x x -<+，可知0x >，故收敛区间为(0,)+∞,当0x =时，1(1)nn n ∞=-∑发散，所以收敛域为(0,)+∞.令11x t x -=+，11111()(1)1n n nn n n n n t f t nt n t t t t ∞∞∞∞+===='⎛⎫==+-=- ⎪-⎝⎭∑∑∑∑2222(1)1(1)t t t t t t t -=-=---，所以幂级数11(1n n x n x ∞=-+∑的和函数211()(14x x s x f x --==+，(0,)x ∈+∞.(Ⅱ)令(,),(,)x xP x y ye y Q x y e x =+=+，可得1x P Qe y x∂∂==+∂∂，所以积分与路径无关.令取路径1:0,:12L y x =→，23:2,:04L x y =→，123222413(00)d (2)d (2).4xL L I e x e y e =+=+++=+⎰⎰⎰⎰（19）解(Ⅰ)222212222101d d d d ()d R R x y R z V V zx y R z zπΩ+≤-===-⎰⎰⎰⎰⎰⎰⎰233111(())23224R R R R π=-=.记2Ω的球冠部分表面为2∑，底面为3∑，其中3∑为半径为2R 的圆，故面积为2233()24R R ππ=，则2Ω的表面积为222222134331d d 44x y R RR S S x y ππ∑+≤=+=+⎰⎰⎰⎰222222003433d d 44x y R R Rx y d r πππθ+≤=+=+⎰⎰⎰⎰222220337)2.444R R R R r R πππππ=--+=-+(Ⅱ)补充平面2223:0()z x y R ∑=+≤，取下侧，22243:()24R z x y R ∑=+≤，取上侧，则34,,∑∑∑围成闭区域1Ω，并取外侧，由高斯公式可得1213113d .8V R π∑+∑+∑Ω==⎰⎰⎰⎰⎰22233d d 0d d 0x y Rz x y x y ∑∑+≤==-=⎰⎰⎰⎰⎰⎰,22244233433d d d d ,2248x y R R R z x y x y R R ππ∑∑+≤===⋅=⎰⎰⎰⎰⎰⎰故43433331130.88I R R R πππ∑+∑+∑∑∑=--=--=⎰⎰⎰⎰⎰⎰（20）解两边取对数，只需1()ln(1)1x xα++>，即11ln(1)x xα>-+.取1t x =，只需求11()ln(1)f t t t=-+在(0,)+∞上的最大值.又2222221(1)1(1)ln (1)()ln (1)(1)ln (1)t t t t f t t t t t t +++-'=-+=+++，令22()(1)ln (1)g t t t t =++-，则2()ln (1)2ln(1)2g t t t t '=+++-，2(ln(1))()01t t g t t+-''=<+，其中(0)0g '=可知()0g t '<；由(0)0g =可知()0g t <，故()0f t '<.于是在(0,)+∞上11()ln(1)f t t t =-+<00111lim ()lim[ln(1)2t t f t t t →+→+=-=+，因此12α≥.(21)解(Ⅰ)二次型的矩阵11211212112n A ⎛⎫- ⎪ ⎪ ⎪- ⎪=⎪ ⎪- ⎪ ⎪ -⎪⎝⎭，因为112100030100240000113220001110i i i r r inn n n A n n n n--+--+==--+，所以各阶顺序主子式102i i i A +=>，1,2,,i n = ，从而()f x 正定.(Ⅱ)111111101101n n Tn n n T T n E A E A P A P A αααα-------⎛⎫⎛⎫-⎛⎫= ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭1111111110.010101n n n n T T n n A A E A A A αααααα---------⎛⎫⎛⎫-⎛⎫== ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭ (Ⅲ)记0(,1)Ty P x =，0121(,,,)Tn x x x x -=，则()100110()1011n T T T T Tn n T n A x f y y A y x P A Px x A αα---⎛⎫⎛⎫=== ⎪⎪-⎝⎭⎝⎭10101(1).T T n n x A x A αα---=+- 因为n A 正定，所以1n A -正定，故0100T n x A x -≥ ，即当0(0,0,,0)x = 时，0100T n x A x -=，从而()f x 在1n x =时的最小值为111.Tn A αα---（22）解（I ）(){}Y F y P Y y =≤①当y μ<时,()0Y F y =②当yμ≥时,(){}{2}Y F y P X y P y X y μμμ=-+≤=-≤≤22()22,x ydx μσμ---=⎰故()222,()0,y Y y f y y μσμμ--⎧≥=<⎩（II ）12()(,)(,)(,)Y Y Y n L f y f y f y μμμμ=⋅2211()2ni i ny u e σ=--∑=⋅12min{,,,}n y y y μ≤2211ln ()ln (),2n i i L n y μμσ==-∑21(ln )12()02ni i d L y d μμσ==⋅⋅->∑故12ˆmin{,,,}n y y y μ= ，即12ˆmin{,,,}n Y Y Y μ= .。

【考研】考研数学一全真模拟卷及解析考研数学一是众多考研学子面临的一大挑战。

为了帮助大家更好地备考，我们精心准备了这份全真模拟卷及详细解析，希望能对大家的复习有所助益。

一、选择题（共 8 小题，每题 4 分，共 32 分）1、设函数＼（f(x) ＝＼frac{1}｛1 ＋ x^2}＼），则＼（f(f(x)）＼）为（）A ＼（＼frac{1}｛1 ＋ 2x^2 ＋ x^4} ＼）B ＼（＼frac{1}｛1 ＋2x^2} ＼） C ＼（＼frac{1}｛1 ＋ x^2} ＼） D ＼（＼frac{x^2}｛1＋ x^2} ＼）解析：因为＼（f(x) ＝＼frac{1}｛1 ＋ x^2}＼），所以＼（f(f(x)）＝＼frac{1}｛1 ＋（＼frac{1}｛1 ＋ x^2}）＾2} ＝＼frac{1}｛1 ＋＼frac{1}｛（1 ＋ x^2)＾2}｝＝＼frac{1 ＋ x^2}｛1 ＋ x^2 ＋ 1} ＝＼frac{1 ＋ x^2}｛2 ＋ x^2} ＼neq\）选项中的任何一个，此题无正确选项。

2、设＼（y ＝ y(x)＼）是由方程＼（e^y ＋ xy e ＝ 0\）所确定的隐函数，则＼（y'（0)＼）的值为（）A －1B 0C 1D 2解析：对方程两边同时对＼（x\）求导，得＼（e^y ＼cdot y' ＋ y＋ x ＼cdot y' ＝ 0\）。

当＼（x ＝ 0\）时，代入原方程得＼（e^y e＝ 0\），解得＼（y ＝ 1\）。

将＼（x ＝ 0\），＼（y ＝ 1\）代入＼（e^y ＼cdot y' ＋ y ＋ x ＼cdot y' ＝ 0\），得＼（e ＼cdot y' ＋ 1 ＝0\），解得＼（y'（0) ＝＼frac{1}｛e}＼）。

3、设＼（f(x)＼）具有二阶连续导数，且＼（f(0) ＝ 0\），＼（f'（0) ＝ 1\），则＼（＼lim_{x ＼to 0} ＼frac{f(x) x}｛x^2}＼）等于（）A ＼（0\）B ＼（＼frac{1}｛2} ＼）C ＼（1\）D 不存在解析：利用泰勒公式，将＼（f(x)＼）在＼（x ＝ 0\）处展开：＼（f(x) ＝ f(0) ＋ f'（0)x ＋＼frac{1}｛2}f'＇（0)x^2 ＋ o(x^2) ＝ x ＋＼frac{1}｛2}f'＇（0)x^2 ＋ o(x^2)＼），则＼（＼lim_{x ＼to 0} ＼frac{f(x) x}｛x^2} ＝＼lim_{x ＼to 0} ＼frac{＼frac{1}｛2}f'＇（0)x^2 ＋ o(x^2)｝｛x^2} ＝＼frac{1}｛2}f'＇（0)＼）。

考研数学（数学三）模拟试卷200(题后含答案及解析) 题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．设f(x)为R上不恒等于零的奇函数，且fˊ(0)存在，则函数A．在x=0处左极限不存在B．有跳跃间断点x=0C．在x=0处右极限不存在D．有可去间断点x=0正确答案：D2．设f(x，y)与φ(x，y)均为可微函数，且φˊy(x，y)≠0，已知(xo，yo)是f(x，y)在约束条件φ(x，y)＝0下的一个极值点，下列选项正确的是( )．A．若fˊx(xo，yo)＝0，则fˊy(xo，yo)＝0B．若fˊx(xo，yo)＝0，则fˊy(xo，yo)≠0C．若fˊx(xo，yo)≠0，则fˊy(xo，yo)=0D．若fˊx(xo，yo)≠0，则fˊy(xo，yo)≠0正确答案：D3．设非齐次线性微分方程yˊ＋P(x)y＝Q(x)有两个不同的解y1(x)，y2(x)，C为任意常数，则该方程的通解是( )．。

A．C[y1(x)－y2(x)]B．y1(x)＋C[y1(x)－y2(x)]C．C[y1(x)＋y2(x)]D．y1(x)+C[y1(x)＋y2(x)]正确答案：B4．下列各选项正确的是( )．A．&nbspB．&nbspC．&nbspD．&nbsp正确答案：A5．设A为3阶矩阵，将A的第2行加到第1行得B，再将B的第1列的一1倍加到第2列得C，记则( )．A．C＝P－1APB．C＝PAP－1C．C＝PTAPD．C＝PAPT正确答案：B6．设向量组α1，α2，α3线性无关，则下列向量组中线性无关的是( )．A．α1＋α2，α2＋α3，α3－α1B．α1＋α2，α2＋α3，α1＋2α2＋α3C．α1＋2α2，2α2＋3α3，3α3＋α1D．α1＋α2＋α3，2α1－3α2＋2α3，3α1＋5α2＋3α3正确答案：C7．设F1(x)与F2(x)分别为随机变量，X1与X2的分布函数，为使F(x)=aF1(x)－bF2(x)是某一随机变量的分布函数，在下列给定的各组数值中应取( )．A．a＝3／5，b＝－2／5B．a＝2／3，b＝2／3C．a＝－1／2，b＝3／2D．a＝1／2，b＝－3／2正确答案：A8．设两个随机变量X与Y独立同分布，P｛X＝－1｝＝P｛Y＝－1｝＝1／2，P｛X＝1｝＝P｛Y＝1｝=1／2，则下列各式中成立的是( )．A．P｛X＝Y｝＝1／2B．P｛X＝Y｝＝1C．P｛X＋Y＝0｝＝1／4D．P｛XY＝1｝＝1／4正确答案：A填空题9．正确答案：10．差分方程yx+1－3yx＝7.2x的通解为_______．正确答案：显然其齐次方程的通解为yx＝C.3x(C为任意常数)．设其特解为yx＝b.2x，所以有b.2x－1－3b.2x＝7.2x，从而得b＝－7．因此，原方程的通解为yx＝C.3x－7.2x．11．正确答案：12．正确答案：13．若四阶矩阵A与B为相似矩阵，A的特征值为1／2、1／3、1／4、1／5，则行列式｜B－1－E｜＝________．正确答案：由已知A与B相似，则A与B的特征值相同，即B的特征值也为1／2、1／3、1／4、1／5，从而B－1－E的特征值为1，2，3，4，因此｜B －1－E｜＝1.2.3.4＝24．14．设总体X的概率密度为而X1，X2…，Xn是来自总体X的简单随机样本，则未知参数θ的矩估计量为_________．正确答案：本题考查矩估计量的求法，由题设，解答题解答应写出文字说明、证明过程或演算步骤。

考研数学（数学一）模拟试卷500(题后含答案及解析) 题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．设当|x|＜1时f(x)＝展开成收敛于它自身的幂级数f(x)＝，则关于它的系数an(n＝0，1，2，…)成立的关系式为A．an＋2＝an＋1＋an．B．an＋3＝an．C．an＋4＝an＋2＋an．D．an＋6＝an．正确答案：D2．当x→0时，下列3个无穷小a＝按后一个无穷小比前一个高阶的次序排列，正确的次序是A．α，β，γ．B．γ，β，α．C．γ，α，βD．α，γ，β正确答案：D3．设f(x)是以T为周期的连续函数(若下式中用到f＇(x)，则设f＇(x)存在)，则以下结论中不正确的是A．f＇(x)必以T为周期．B．必以T为周期．C．必以T为周期．D．必以T为周期．正确答案：B4．设S为球面x2＋y2＋z2＝R2(常数R＞0)的上半部分，方向为上侧．则下述对坐标的曲面积分(即第二型曲面积分)不为零的是A．B．C．D．正确答案：B5．设a1，a2，…，as，是线性方程组的s个互不相同的解向量，则向量组{ai一aj| i≠j，i＝1，2，…，s；j＝1，2，…，s}的秩r取值范围为A．1或2．B．2或3．C．D．1.正确答案：A6．已知P－1AP＝，α1是A的属于λ1＝1的特征向量，α2，α3是A 的属于λ2＝－1的线性无关的特征向量，则矩阵P是A．(α2，α1，α3)．B．(α1，α2一α3，α3－α1)．C．(3α1，α2＋α3，α2一α3)．D．(2α2，3α3，α1)．正确答案：C7．将一枚均匀硬币连续抛n次，以A表示“正面最多出现一次”，以B表示“正面和反面各至少出现一次”，则A．n＝2时，A与B相互独立．B．n＝2时，．C．n＝2时，A与B互不相容．D．n＝3 时，A与B相互独立．正确答案：D8．设总体X～N(0，σ2)(σ2已知)，X1，…，Xn是取自总体X的简单随机样本，S2为样本方差，则下列正确的是正确答案：C填空题9．设空间曲线L : 其中常数a＞0．则空间第一型曲线积分＝_____________.正确答案：解析：平面x—y＝0经过球面．x2＋y2＋z2＝a2的中心，所以L是一个半径为a的圆周．今建立它的参数方程．将L投影到xOz平面上去，为此，消去y，得所以L在xOz平面上的投影是一个椭圆．引入此椭圆的参数方程：x＝，0≤t ≤2π由于L在平面x—y＝0上，所以L的参数方程为x＝于是ds＝所以10．设an＝x(1－x)n－1dx,则＝_____________.正确答案：1—21n 2解析：an＝11．微分方程y＂＋2y＇一3y＝x(ex＋1)的通解为y＝___________．正确答案：，其中C1，C2为任意常数解析：该常系数线性微分方程对应的齐次方程的特征方程为r2＋2r一3＝(r 一1)(r＋3)＝0，特征根r1＝1，r2＝一3，对应的齐次方程的通解为Y＝C1ex＋C2e-3x，其中C1，C2为任意常数．原给非齐次微分方程y＂＋2y＇一3y＝x(ex ＋1)＝xex＋x，可分解成两个非齐次方程y2＋2y＇一3y＝xex与y＂＋2y＇一3y＝x，用常用的待定系数法，可求得各自的特解分别为所以原给方程的通解为y＝其中C1，C2为任意常数．或写成如上所填．12．设y＝y(x)由方程x＝确定，则＝_____________.正确答案：一2π解析：将x＝0代入x＝有y＝1．再将所给方程两边对x求导，得1＝于是y＇＝将x＝0，y＝1代入，得＝一2π．13．设xi≠0，i＝1，2，3，4．则行列式D＝＝_______________.正确答案：解析：将D的第1行的一l倍加到2，3，4行，再将第i列(i＝2，3，4)的倍加到第1列，得D14．已知随机变量X在(1，2)上服从均匀分布，在X＝x条件下Y服从参数为x的指数分布，则E(XY2)＝_____________．正确答案：21n 2解析：由题设知所以(X，Y)的联合概率密度为F(x，y)＝所以E(XY2)＝解答题解答应写出文字说明、证明过程或演算步骤。

2023年研究生《数学三》模拟卷2 2023年研究生《数学三》模拟卷2
1.[单选][4分]
2.[单选][4分]
3.[单选][4分]
4.[单选][4分]
A. n必为2
B. n必为4
C.n为1或2
D.n为2或4
5.[单选][4分]
6.[单选][4分]
A. 连续，但不可偏导
B. 可偏导，但不连续
C. 连续、可偏导，但不可微
D. 可微
7.[单选][4分]关于函数的极值个数，正确的是
A. 有2个极大值，1个极小值
B. 有1个极大值，2个极小值
C. 有2个极大值，没有极小值
D. 没有极大值，有2个极小值
8.[问答][10分]
9.[问答][10分]
10.[问答][10分]
11.[问答][10分]
12.[问答][10分]
13.[问答][10分]
14.[问答][10分]
15.[问答][10分]
16.[问答][10分]
17.[问答][10分]
18.[问答][10分]
19.[问答][10分]
20.[问答][10分]
21.[问答][10分]
22.[问答][10分]某企业生产某种商品的成本函数为a,b,c,l,s都是正常数，Q为销售量，求：（I）当每件商品的征税额为t时，该企业获得最大利润时的销售量；（II）当企业利润最大时，t为何值时征税收益最大.。

全国硕士研究生入学统一考试数学(三)试卷（模拟考试）身份证号 姓名 电话 成绩数学三答题号及分值：(4+2+2，4+1+1，5+2+2)1-8题共32分9-14共24分 15 10分1610分1710分1810分1910分20 11分2111分2211分2311分成绩一、选择题（本题共8小题，每小题4分，满分32分. 每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内） 1．函数∫++=xdt t t x f 02)1ln()(为（）。

(A)偶函数,且在上为单调减。

(B)偶函数，且在),0(+∞),0(+∞上为单调增。

(C)奇函数，且在上为单调减。

(D)奇函数，且在),0(+∞),0(+∞上为单调增。

【解】 答案：（B）。

（函数奇偶性，定积分的换元积分公式） 因为对任意的),(+∞−∞∈x ，∫++=xdt t t x f 02)1ln()(都存在，且∫∫−−++−=++=−−xxdu u u dt t t x f 0202))()(1ln()1ln()()()1ln(11ln202x f du u u du u u xx=++=++−=∫∫。

所以∫++=xdt t t x f 02)1ln()(是偶函数，且在),0(+∞上0)1ln()(2>++=′x x x f 。

2．设在的某邻域内有二阶连续导数，且满足)(x f 0=x 1)1ln()(lim 30=+→x x f x , 则（ ）。

(A),,在0)0(=′f 0)0(≠′′f )(x f 0=x 处有极值(B),在处有极值0)0()0(=′′=′f f )(x f 0=x (C), 在处取得拐点0)0()0(=′′=′f f 0=x (D), 在处取得拐点0)0(,0)0(=′′≠′f f 0=x 【解】13)(lim )(lim )1ln()(lim203030=′==+→→→x x f x x f x x f x x x ，0)0(=′f ，)(x f ′在0=x 的两侧不变号，因此不为极值点。

考研数学模考试卷数学三模考试卷一．选择题：第1～8小题，每小题4分，共32分.下列每题给出的四个选项中,只有一个选项符合试题要求.()1设函数()x f 在点0=x 处有()00=f ,()10-='f ,则()[]x x x f sin 1021lim +→=()A 2. ()B 2-e. ()C 21e . ()D 2e . ()2函数()x x x x f sin 3-=的不可导点的个数为()A 1. ()B 2. ()C 3. ()D 4.()3设()()()()()()()n x x x n x x x x f +++---= 2121,则()1f '= ()A ()11+n n . ()B ()()111+--n n n . ()C 11+n . ()D ()11+-n n.()[]3,14设正项级数∑∞=1n n a收敛，则()∑∞=+11ln n n a λ ()为常数0>λ, ()A 收敛. ()B 发散. ()C 收敛性不定. ()D 敛散性与λ有关.()5设A 为n m ⨯矩阵,已知()m A R =,且方程组0=Ax 有非零解,则下列选项中不正确的是()A n m <. ()B n m ≥.()C A 的列向量线性相关. ()D β=Ax 有无穷多组解.()6已知3阶方阵A 不是可逆矩阵，βα,是3维列向量，且βα≠，βα-≠，若满足βα=A ，αβ=A ，则下述结论正确的是()A A 不能与对角矩阵相似.()B A 能与对角矩阵⎪⎪⎪⎭⎫ ⎝⎛-100010000相似.()C A 能与对角矩阵⎪⎪⎪⎭⎫ ⎝⎛100000000相似.()D A 能与对角矩阵⎪⎪⎪⎭⎫ ⎝⎛-100000000相似.. 给大家分享点个人的秘密经验，让大家考得更轻松。

在这里我想跟大家说的是自己在整个考研过程中的经验以及自己能够成功的考上的捷径。

首先就是自己的阅读速度比别人的快，考试过程中的优势自然不必说，平时的学习效率才是关键，其实很多人不是真的不会做，90%的人都是时间不够用，要是给足够的时间，估计很多人能够做出大部分的题。

考研数学模拟试卷一【数三】一、选择题：1～8小题，每小题4分，共32分.下列每题给出的四个选项中，只有一个选项是符合题目要求的，请将所选项前的字母填在答题纸指定位置上. (1) 设⎰⎰⎪⎭⎫⎝⎛+==x xdt t dt t t sin 050,11,sin βα则当0→x 时，α是β的_____ （ ）（A ）高阶无穷小. （B ）低阶无穷小.（C ）等价无穷小. （D ）同阶但非等价无穷小.（2）设函数()f x 有二阶连续导数，且0()1lim01cos x f x x →-=-，01x →''=，则 ( ) (A)()f x 在点0x =处取极大值 (B)()f x 在点0x =处取极小值 (C)点(0,(0))f 是曲线()y f x =的拐点(D)点0x =不是()f x 的极值点，点(0,(0))f 也不是()y f x =的拐点（3）设01p <≤，级数11sin()1n pnn x dx x π∞+=+∑⎰( ) (A)绝对收敛 (B)条件收敛 (C)发散 (D)敛散性与p 有关(4) 已知⎰='28)()(dx x f x f ，且0)0(=f ，则⎰2)(dx x f 等于 （ ）（A ）2 （B ）2± （C ）4 （D ）4±（5）设A 是n m ⨯矩阵，B 是s n ⨯矩阵，则方程组0=Bx 与0=ABx 同解的充分条件是 （ ）（A ）n A r =)( ； （B ）m A r =)(； （C ） n B r =)(； （D ）s B r =)(.(6)已知⎪⎪⎪⎭⎫ ⎝⎛=x A 00110002的伴随矩阵*A 有一特征值为2-，则=x （ ）12)(或-A ； 11)(或-B ； 12)(--或C ； 11)(-或D(7)设随机变量,X Y 相互独立且均服从正态分布2(,)N μσ，若概率1()2P aX bY μ-<=则 （ ）（A ）11,22a b ==；（B ）11,22a b ==-；（C ）11,22a b =-=；（D ）11,22a b =-=-；(8)设随机变量)1(~),21,2(~),1,0(~321E X B X N X ，设⎪⎪⎪⎭⎫⎝⎛=233322222111EX DX EXEX DX EX EX DX EX A ，则矩阵A 一定是 （ ）)(A 可逆阵； )(B 不可逆阵； )(C 对称阵； )(D 反对称阵。