正方体涂色规律公式

32×6＝54
1面涂色的小正方体的个数都是6的倍数。
如果用n表示把大正方体的棱平均分的份数，用a、b分别表示
2面涂色和1面涂色的小正方体的个数，你能用式子分别表示n
和a、b的关系吗？
a=12(n －2) b=6(n －2)2
找各种小正方体时， 各种小正方体的个
要注意它们在大正 数与正方体顶点、
方体上的位置。
谢谢观看
表面涂色的正方体
一个表面涂色的正方体，每条楞都平均分成2 份。如果照下边的样子把它切开，能切成多少个 同样大的小正方体？每个小正方体有几个面涂色？
如果像下图这样把正方体切开，能切成多少个小 正方体？切成的小正方体中，3面涂色、2面涂色、 1面涂色的各有多少个，分别在什么位置？
3面涂色的在每个顶点处，有8个。
3面涂色的小正方体有8个。源自3×12＝36（个） 2面涂色的小正方体有36个。
32×6＝54（个） 1面涂色的小正方体有54个。
3面涂色的小正方体都在大正方体顶 点的位置，都是8个。
1×12＝12
2×12＝24
3×12＝36
2面涂色的小正方体的个数都是12的倍数。
12×6＝6
22×6＝24
面和棱的个（条）
数有关。
要把找、数、算等 方法结合起来，并 根据图形的特征进 行思考。
小结： 把棱长为几厘米的小正方体涂色后切成棱长为1厘米的小正 方体，涂色面的规律： （1）3面涂色的小正方体个数=正方体的订点个数=8个; （2）2面涂色的小正方体个数
=正方体棱的条数乘棱长减2的差 =12×（n -2); （3）1面涂色的小正方体个数 =正方体的面数乘棱长将2的差的平方 =6×（n -2)²。
2面涂色的在每条棱的中间位置处，有12个。

涂色技巧：在涂色 时，可以采用“跳 步涂色法”，即先 涂一个面，再跳过 一个面涂下一个面， 以此类推，直至涂 完所有的面。
涂色顺序：在涂色 时，可以采用“从 上到下”、“从左 到右”、“从外到 内”等顺序进行涂 色，以保证每个面 都有一个不同的颜 色。
正方体的表面涂色问题实例解析
3面涂色：只在棱 上出现，代表顶 点
涂色规律在其他形状上的推广：可添加标题
添加标题
添加标题
涂色规律在不同维度上的推广：可 以应用于三维、四维等更高维度的 正方体表面涂色问题。
涂色规律在其他领域的应用：可以 应用于计算机图形学、建筑学等领 域。
正方体的表面涂 色问题
正方体的表面涂色问题概述
感谢您的观看
汇报人：XX
计算机图形学： 涂色规律可以应 用于计算机图形 学中，实现更逼 真的三维模型渲 染效果。
物理学模拟：涂 色规律可以应用 于物理模拟中， 如量子力学和分 子动力学的模拟。
游戏开发：涂色 规律可以应用于 游戏开发中，如 角色皮肤和场景 的渲染。
涂色规律的推广
涂色规律的应用范围：适用于所有 正方体表面涂色问题，包括大、中、 小正方体。
涂色方法：可以采用递归、数学归纳法等方法证明涂色规律，并给出具体的涂色方案。
应用领域：表面涂色问题在计算机图形学、组合数学等领域有广泛应用，可以用于设 计图案、解决几何问题等。
对未来研究的展望
深入研究不同涂色方式对正方体表面涂色问题的影响 探索更高效的算法和计算模型，以解决大规模正方体表面涂色问题 结合其他领域的知识，如计算机图形学、统计学等，对正方体表面涂色问题进行多角度研究 拓展正方体表面涂色问题的应用场景，将其应用于实际问题的解决中
2面涂色：在棱上 出现，代表棱上 非顶点

当n =10时,3面涂色的小正方体有_8___个， 2面涂色的小正方体有_9_6__个， 1面涂色的小正方体有3__8_4_个，
各面无涂色的小正方体有5__1_2_个。
总结回顾 回顾今天的探究和发现的过程，说
说你有什么方法上的收获？
● 化繁为简的方法。
从简单的情况入手找规律，用规律解决复杂的问题。
人教版小学数学五年级下册
正方体涂色问题
知识回顾
1cm
1cm 1cm
6 个面 8 个顶点 12 条棱
引入问题
1cm 1cm 1cm
如果用棱长1cm的小正方体拼成一个棱长 10厘米的大正方体，需要多少块？
探索规律
如果给这个大正方体的表面涂上红色
小组合作
研究问题一：
同类涂色的小正方体分别在大正方体的什么位置？
●分类计数的方法。
两面涂色的小正方体块数=每条棱上两面涂色的块数X12
（棱上块数-2） 两 面 涂 色
我发现：
一面涂色的小正方体块数=每个面一面涂色块数 X6
一 面 涂 色
没
有
13
23
33
涂
色
Hale Waihona Puke 我发现：没有涂色的小正方体=（每条棱上小正方体块数-2）³
当棱上块数为n时： 没有涂色的新正方体
的棱上块数为 (n-2)
(n-2) (n-2)
(n-2)
棱上块数为n
小正方体表面涂色的规律
n
8
12(n-2) 6(n-2)2 ( n-2)3
应用规律： 给用棱长1cm的小正方体的拼成棱长10cm的大
正方体表面涂上红色，三面涂色、两面涂色、一 面涂色、没有涂色的小正方体各有多少个？

05
正方体涂色的物理原理
光的反射和吸收
光的反射
当光线照射到物体表面时，一部分光线会被反射回来，另一部分则被吸收或穿透。不同颜色的物体对 光的反射和吸收特性不同，因此呈现出不同的颜色。
光的吸收
物体对光的吸收能力取决于其表面涂层的颜色和厚度。涂层颜色越深，对光的吸收能力越强，反射的 光线越少，反之亦然。
虚拟现实
在虚拟现实中，涂色正方体可以作 为虚拟物体，为用户提供沉浸式的 体验。
04
正方体涂色的数学原理
欧拉公式
总结词
欧拉公式是数学中一个重要的公式，用于计算多面体的面数 、棱数和顶点数之间的关系。
详细描述
欧拉公式是由数学家莱昂哈德·欧拉发现的，它表示多面体的面 数（F）、棱数（E）和顶点数（V）之间的关系为：F + V - E = 2。对于正方体，这个公式可以帮助我们理解其几何结构。
数学教育
涂色正方体可以作为教学 工具，用于教授几何学、 数学建模等课程，帮助学 生更好地理解抽象概念。
计算机图形学应用
3D渲染
涂色正方体是计算机图形学中常 用的模型之一，可用于3D渲染和 动画制作，创建逼真的视觉效果。
游戏开发
在游戏开发中，涂色正方体可以作 为游戏元素，用于构建游戏场景、 角色和道具等。
02
正方体的涂色规律
顶点涂色规律
总结词
每个顶点涂色方式相同，均为3种 颜色中的一种。
详细描述
正方体有8个顶点，每个顶点都可 以涂上3种不同的颜色中的一种， 因此顶点的涂色方式共有3^8种 。
棱涂色规律
总结词
每条棱的涂色方式相同，均为3种颜色中的一种。
详细描述
正方体有12条棱，每条棱都可以涂上3种不同的颜色中的一种，因此棱的涂色方式共有3^12种。

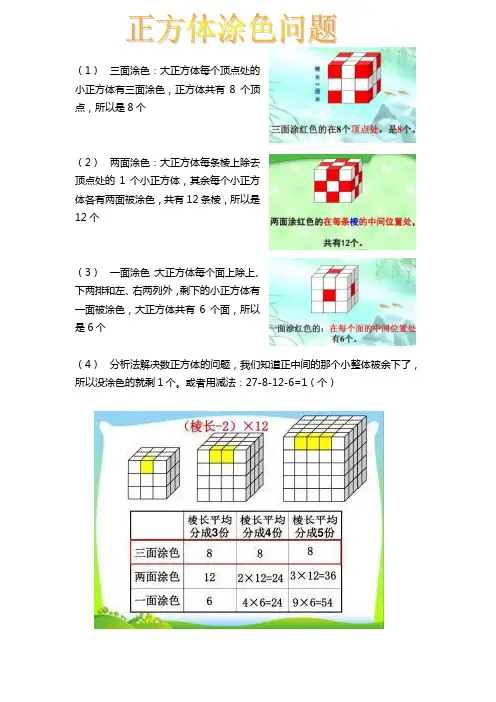
（1）三面涂色：大正方体每个顶点处的
小正方体有三面涂色，正方体共有8个顶
点，所以是8个
（2）两面涂色：大正方体每条棱上除去
顶点处的1个小正方体，其余每个小正方
体各有两面被涂色，共有12条棱，所以是
12个
（3）一面涂色：大正方体每个面上除上、
下两排和左、右两列外，剩下的小正方体有
一面被涂色，大正方体共有6个面，所以
是6个
（4）分析法解决数正方体的问题，我们知道正中间的那个小整体被余下了，所以没涂色的就剩1个。

或者用减法：27-8-12-6=1（个）
正方体涂色专项练习
【练习1】
如图是用27个小正方体拼成的一个大正方体，把它的
表面都涂成红色
请你数一数，算一算：每条棱上3个小正方体，a=3
（1）三面涂成红色的小正方体有（8）块；
（2）两面涂成红色的小正方体有（12）块；
（3）一面涂成红色的小正方体有（6）块；
（4）没有涂成红色的小正方体有（1）块。

【方法总结】
用若干个小正方体拼成一个大正方体，并将拼成的大正方体的表面涂色。

如果大正方体的每条棱上有a个小正方体，则
三面涂色的小正方体在顶点处，共有8 个；
两面涂色的小正方体在棱上，共有[(a-2)×12] 个；
一面涂色的小正方体在面上，共有[(a-2)×(a-2)×6] 个。

表面涂色的正方体
将棱长为3的正方体的表面刷上 黄色的漆，再将其分割成棱长为1的 小正方体。
其中三面、两面、一面涂色的 小正方体各有多少个？
8个
三面涂色
12个
两面涂色
6个
一面涂色
三面、两面、一面涂色的小正方体 各在原正方体的什么位置？
三面涂色
顶点
两面涂色
棱的中间
一面涂色
面的中间
如果正方体的棱长是4、5，其中三 面、两面、一面涂色的小正方体各 有多少个？
没有 涂色
棱长为3 13
棱长为4 23
棱长为5 棱长为n
33
（ n -2）3
①
②
③
棱长为4 三面涂色 8 两面涂色 一面涂色
棱长为4 三面涂色 8 两面涂色 2×12=24 一面涂色
棱长为4 三面涂色 8 两面涂色 2×12=24 一面涂色 4×6=24
棱长为5 三面涂色 8 两面涂色 一面涂色
棱长为5 三面涂色 8 两面涂色 3×12=36 一面涂色
棱长为5 三面涂色 8 两面涂色 3×12=36 一面涂色 9×6=54
（棱长-2）2×6
12
22
32
棱长为3 棱长为4 棱长为5
三面涂色 8
8
8
两面涂色 12 2×12=24 3×12=36
一面涂色
6
4×6=24 9×6=54
棱长为3 棱长为4 棱长为5 棱长为n
三面涂色 8
8
8
8
两面涂色 12 2色 6
4×6=24 9×6=54 （n -2）2×6
仔细观察表格，比一比，从中你发 现了什么？
棱长为3 棱长为4 棱长为5
三面涂色 8

涂色面的排列规律
总结词
涂色面按照一定的规律排列
详细描述
正方体的涂色面遵循一定的排列规律。对于一个给定的正方体，其涂色面的排列顺序是 固定的，不会因为边长的变化而改变。
涂色面的对称性
总结词
正方体的涂色面具有对称性
VS
详细描述
正方体的涂色面具有对称性，这种对称性 可以通过旋转或翻转正方体来观察。例如 ，一个涂色的正方体可以沿其中心轴旋转 90度或180度，其涂色面的排列顺序不会 发生变化。
详细描述
正方体的六个面中，有四个相邻的面被涂上颜色，通常是前 面、右面、上面和后面或左面、右面、上面和下面。
03
正方体的涂色规律
涂色面的数量与正方体的边长关系
总结词
正方体的涂色面数量与边长成正比关 系
详细描述
随着正方体边长的增加，涂色面的数 量也会相应增加。例如，一个边长为 1的正方体有6个涂色面，而边长为2 的正方体则有12个涂色面。
正方体的性质
总结词
正方体具有一些独特的性质，包括对称性和空间关系。
详细描述
正方体的六个面都是中心对称的，即如果一个面围绕其中心旋转180度，它将与另一个面对齐。此外，正方体的 空间关系也很特殊，例如它的对角线长度是边长的√3倍。
正方体的应用
总结词
正方体的应用广泛，包括建筑、艺术和科学领域。
详细描述
艺术创作中的应用
绘画
设计作品
表面涂色正方体可以作为绘画的素材 和灵感来源，帮助艺术家创造出独特 的艺术作品。
表面涂色正方体也可以用于设计各种 艺术作品，如首饰、家居用品等，增 加作品的艺术价值和观赏性。
雕塑
在雕塑创作中，表面涂色正方体可以 用于塑造立体感和质感，增强雕塑的 表现力和视觉冲击力。

正方体涂色规律
嘿，朋友们！今天咱来聊聊正方体涂色规律这个有趣的事儿。

你看啊，这正方体就像是个小小的魔法盒子，表面涂上颜色，那可就有大学问啦！想象一下，一个普普通通的正方体摆在你面前，就像个等待被探索的小秘密基地。

要是给这个正方体的每个面都涂上一种颜色，哇，那一下子就变得五彩斑斓了。

可这里面的规律你发现了吗？咱就说，从一个面开始看，它就只有一种颜色呀，多简单明了。

但要是再看看相邻的面呢？它们的颜色可就不一样啦，这就好像是不同性格的小伙伴凑在一起，各有各的特点。

再往深了研究，要是把正方体切成好多小块呢？那可就更有意思啦！每一小块都有自己独特的涂色情况。

有的可能一面有颜色，有的可能两面有颜色，还有的可能更多面呢！这就好比是一个大班级里，每个同学都有自己独特的闪光点。

你说这正方体的涂色规律是不是特别神奇？就像生活中的好多事情一样，表面看起来普普通通，但是只要你细心去观察、去研究，就能发现其中隐藏的奥秘。

比如说，我们每天走的路，看起来都差不多，但如果你仔细留意路边的小花小草，或者是天上的云朵，是不是就能发现不一样的美好呢？这正方体涂色规律不也是这样嘛！
而且啊，通过研究这个正方体涂色规律，还能锻炼我们的思维能力呢！让我们学会从不同的角度去看待问题，去分析问题。

这可不是一般的厉害呀！
你再想想，要是在一个聚会上，你突然跟大家聊起正方体涂色规律，那得多有意思呀！大家肯定会觉得你这人真有创意，真有趣。

总之呢，这正方体涂色规律可真是个宝，它不仅有趣，还能让我们学到好多东西。

咱可别小瞧了它，要好好去研究研究，说不定还能发现更多意想不到的惊喜呢！大家说是不是呀！
原创不易，请尊重原创，谢谢!。

涂色正方体个数公式好的，以下是为您生成的文章：咱们在学习数学的时候，经常会碰到各种各样有趣又有点小挑战的问题，就比如说这个“涂色正方体个数公式”。

我记得有一次，在课堂上，我给学生们出了一道这样的题：一个大正方体的表面被涂上了颜色，然后把它切成了很多小正方体，问涂了一个面、两个面、三个面的小正方体分别有多少个。

当时啊，教室里一下子就热闹起来了，孩子们有的抓耳挠腮，有的眉头紧皱，还有的已经开始拿笔在纸上写写画画。

这时候，一个平时很机灵的小家伙举手说：“老师，这也太难了，有没有啥诀窍啊？”我笑着告诉他，别着急，咱们一起来找找规律，这就引出了咱们今天要说的“涂色正方体个数公式”。

先来说说涂一个面的小正方体个数。

假设大正方体的边长是 n ，那么涂一个面的小正方体个数就是 (n - 2)×(n - 2)×6 。

为啥是这样呢？咱们来想象一下，一个大正方体，它表面的那一层去掉，里面没涂色的部分组成的小正方体，每个面的边长就少了 2 ，所以一个面的数量就是 (n - 2)×(n - 2) ，然后正方体有 6 个面，再乘以 6 。

再看看涂两个面的小正方体个数，这个公式是 (n - 2)×12 。

这又咋理解呢？咱们想想啊，涂两个面的小正方体，不就是在大正方体的棱上嘛，每条棱上除去两个顶点，中间那部分就是涂两个面的，而正方体有 12 条棱，所以就是 (n - 2)×12 。

最后是涂三个面的小正方体个数，这个就简单啦，只有大正方体的顶点处的小正方体才会涂三个面，正方体有 8 个顶点，所以涂三个面的小正方体个数就是 8 。

掌握了这个公式，咱们来解决一下刚才的那道题。

比如说大正方体的边长是 5 ，那涂一个面的小正方体个数就是 (5 - 2)×(5 - 2)×6 = 3×3×6 = 54 个；涂两个面的就是 (5 - 2)×12 = 3×12 = 36 个；涂三个面的就是 8 个。

数学题求一面涂色两面涂色三面涂色的公式是什么
一面涂色：6（n-2）²
两面涂色：12（n-2）
三面涂色：8
减2都是长宽高截成的个数减2，不是长度减2，因为有时截成的不一定是1个单位。

全无指的是全不涂色，就是长宽高上截成的正方体个数分别减2，然后再相乘。

一面指的是一面涂色的，长宽高个数减2后，再当成表面积来求。

两面指的是两面涂色的，长宽高个数减2后的和相加再乘4。

三面涂色都是8个，三面涂色在上下角落，都是4个，一共是8个。

按角分
判定法：
1、锐角三角形：三角形的三个内角都小于90度。

2、直角三角形：三角形的三个内角中一个角等于90度，可记作Rt△。

3、钝角三角形：三角形的三个内角中有一个角大于90度。

数学———正⽅体涂⾊问题 将⼀个正⽅体的表⾯涂上颜⾊.把正⽅体的棱等分,然后沿等分线把正⽅体切开,能够得到个⼩正⽅体,通过观察我们可以发现个⼩正⽅体全是个⾯涂有颜⾊的. 如果把正⽅体的棱三等分,然后沿等分线把正⽅体切开,能够得到27个⼩正⽅体,我们可以发现这些⼩正⽅体中有8个是三⾯涂有颜⾊的,有12个是两⾯涂有颜⾊的,有6个是⼀⾯涂有颜⾊的,还有1个⾯没有涂⾊. 如果把正⽅体的棱四等分,然后沿等分线把正⽅体切开,能够得到64个⼩正⽅体,我们可以发现这些⼩正⽅体中有8个是三⾯涂有颜⾊的,有24个是两⾯涂有颜⾊，有24个⾯是⼀⾯涂有颜⾊的，还有8个⾯没有涂⾊。

如果把正⽅体的棱五等分,然后沿等分线把正⽅体切开,能够得到125个⼩正⽅体,我们可以发现这些⼩正⽅体中有8个是三⾯涂有颜⾊的,有36个是两⾯涂有颜⾊，有54个⾯是⼀⾯涂有颜⾊的，还有27个⾯没有涂⾊。

如果把正⽅体的棱n等分,然后沿等分线把正⽅体切开,能够得到n3个⼩正⽅体,我们可以发现这些⼩正⽅体中有 8个是三⾯涂有颜⾊的,有12(n-2)个是两⾯涂有颜⾊，有6(n-2)(n-2)个是⼀⾯涂有颜⾊的，还有(n-2)3个⾯没有涂⾊。

例：将棱长4厘⽶的正⽅体表⾯涂成蓝⾊，再将它锯成棱长1厘⽶的⼩正⽅体，则三⾯涂蓝，两⾯涂蓝，⼀⾯涂蓝和没有颜⾊的⾯各⼏个？ 解： 1、以原来⼤正⽅体的顶点为顶点的⼩正⽅体才有可能三⾯涂⾊，共8个。

2、两个⾯相交成⼀条棱，所以只有以原来⼤正⽅体的棱为⼀条棱【此时不包括顶点】的⼩正⽅体才有可能两⾯涂⾊，⼀条棱上两⾯涂⾊的⼩正⽅体2个，12条棱共有12*2=24个。

3、⼀⾯涂⾊的正⽅体是被三⾯涂⾊和两⾯涂⾊的正⽅体包围在中间，且在⼤正⽅体表⾯的，原⼤正⽅体⼀⾯有（4-2）*（4-2）=4个，6个⾯有6*4=24个。

4、没有涂⾊的⼩正⽅体有：4*4*4-8-24-24=8个或（4-2）*（4-2）*（4-2）=8个。

（4）没有涂黄色的的小正方体的个数 =
谢 谢
谢 谢
棱长4厘米
棱长4米
棱长4厘米
棱长4厘米
棱长5厘米
有一个棱长10分米的正方体，它的6个面都涂有黄色，把它切 成棱长1分米的小正方体。 （1）3面涂黄色的的小正方体的个数 =
8
（2）2面涂黄色的的小正方体的个 数 = （10-2）×12=96 （3）1面涂黄色的的小正方体的个 数 =
（10-2）2×6=384
（4）没有涂黄色的的小正方体的个数 =
（10-2）3 =512
有一个长10分米、宽8分米、高6分米的长方体，它的6个面都 涂有黄色，把它切成棱长1分米的小正方体。 （1）3面涂黄色的的小正方体的个数 = （2）2面涂黄色的的小正方体的个 数 = （3）1面涂黄色的的小正方体的个 数 =
探 索 规 律
表面涂色的正方体
棱长3厘米
棱长3厘米
顶 点
棱长3厘米
棱长3厘米
每 条 棱 的 中 间
棱长3厘米
棱长3厘米
每 个 面 的 中 间
棱长3厘米
每 个 面 的 中 间
棱长3厘米
每 个 面 的 中 间
棱长3厘米
3厘米
每 个 面 的 中 间
正 方 体 的 中 心
棱长3厘米
棱长4厘米