2015届宁夏银川市唐徕回民中学高三下学期期中考试(三模)文科数学试题及答案

2013年宁夏银川市唐徕回民中学高考数学三模试卷（文科）一、选择题（每小题5分，共60分）+22．（5分）下面是关于复数的四个命题P1：复数z的共轭复数为1+iP2：复数z的实部为1P3：复数z对应的向量与复数1+i对应的向量垂直P4：解：由于复数==1|z|=3．（5分）已知回归方程=0.85x﹣85.7，则该方程在样本（165，57）处的残差为（）2=0.85x4．（5分）一个简单几何体的正视图、侧视图如图所示，则其俯视图可能是 ①长、宽不相等的长方形 ②正方形 ③圆 ④椭圆（ ）5．（5分）若实数x 、y 满足，则3x •9y的最大值是（ ）6．（5分）双曲线的一个焦点与抛物线x2=8y的焦点相同，一条渐近线与x﹣y+3=0平行，则该双曲线的标．﹣=1∴可设双曲线的方程为：﹣=±=1∴该双曲线的标准方程为﹣7．（5分）（2010•温州二模）如图所示的算法流程图中输出的最后一个数为﹣55，则判断框中的条件为（）8．（5分）在边长为2的正方形中，有一个封闭曲线围成的阴影区域D，现用随机模拟的方法进行了100．4=由概率的几何概型知，则=．的面积为9．（5分）已知f（x）=x2+（sinθ﹣cosθ）x+sinθ（θ∈R）的图象关于y轴对称，则2sinθcosθ+cos2θ．===0，﹣，=2×+0=1，）×（﹣）．6，所以a=所以四面体的棱长为：11．（5分）在椭圆中，F 1，F 2分别是其左右焦点，若|PF 1|=2|PF 2|，则该椭圆离心．代入得，，即，故，又故该椭圆离心率的取值范围是12．（5分）已知f （x ）=x 3﹣6x 2+9x ﹣abc ，a ＜b ＜c ，且f （a ）=f （b ）=f （c ）=0．现给出如下结论： ①f（0）f （1）＞0； ②f（0）f （1）＜0；③f（0）f （3）＞0； ④f（0）f （3）＜0； ⑤abc＜4； ⑥abc＞4．二、填空题（每小题5分，共20分）13．（5分）（2012•德州一模）若向量，满足，，，则向量与的夹角等于．故答案为14．（5分）已知函数y=sinx+cosx，，则下列结论中，正确的序号是③．①两函数的图象均关于点（，0）成中心对称；②两函数的图象均关于直线成轴对称；③两函数在区间（，）上都是单调增函数；④两函数的最小正周期相同．y=sinx+cosx=，①x=﹣时，=0，图象关于点（时，，图象不关于点（的图象不关于直线成轴对称；于直线③x∈（，）时，，函数y=∈（，）时，，函数在区间（，④y=sinx+cosx=15．（5分）某单位有年轻职工21人，中年职工14人，老年职工7人．现采用分层抽样方法从这些职工中选6人进行健康调查．若从选取的6人中随机选2人做进一步的调查，则选取的2人均为年轻人的概率是．均为年轻人的取法有种，所有的抽法有解：每个个体被抽到的概率等于，故应抽取年轻人的数量为21×8人均为年轻人的取法有=，．16．（5分）在△ABC中，∠A=60°，BC=，则AC+AB的最大值为2．，cosA=cos60°===3AB•AC+3≤∴AB+AC≤22三、解答题：本大题共5小题，共70分．解答应写出文字说明，证明过程或演算步骤．17．（12分）已知正项数列满足4S n=（a n+1）2．（1）求数列{a n}的通项公式；（2）设b n=，求数列{b n}的前n项和T n．====所以18．（12分）如图，四棱锥P﹣ABCD的底面是菱形，∠ABC=60°，PA⊥底面ABCD，E、F分别是BC、PC的中点，PA=AB=2．（1）求证：AE⊥PD；（2）求三棱锥A﹣EFC的体积．10∴FOAE=2sin60°=，××AE×EC×FO××1×1．（参考公式：）（2）设乙队员投球次数为x，投中为y，根据上表，利用统计中的最小二乘法原理建立的回归方程为，其中=0.44，若乙队员某场比赛中投球28次，估计投中了多少次．=12=13s=8.75s，其中=0.44，时，20．（12分）（2012•保定一模）已知椭圆C：的离心率为，且过点Q（1，）．（1）求椭圆C的方程；（2）若过点M（2，0）的直线与椭圆C相交于A，B两点，设P点在直线x+y﹣1=0上，且满足（O为坐标原点），求实数t的最小值．，设椭圆方程为由在椭圆，得（∵e=设椭圆方程为在椭圆上，，解得∴椭圆方程为．，得（12，∈，，∴（，，∴t=∵k∈=k=21．（12分）（2013•哈尔滨一模）已知函数f（x）=lnx，g（x）=e x．（ I）若函数φ（x）=f（x）﹣，求函数φ（x）的单调区间；（Ⅱ）设直线l为函数的图象上一点A（x0，f （x0））处的切线．证明：在区间（1，+∞）上存在唯一的x0，使得直线l与曲线y=g（x）相切．相切于点，进而可得，（Ⅰ）解：=，（Ⅱ）证明：∵，∴，的方程为，①（，，∴也为．，四、选做题：请考生在22，23，24题中任选一题作答，如果多做，则按所做的第一题记分．作答时用2B 铅笔在答题纸卡上把所选的题目对应的标号涂黑．（10分）22．（10分）（2013•哈尔滨一模）选修4﹣1：几何证明选讲14如图，AB是⊙O的直径，弦BD，CA的延长线相交于点E，EF垂直BA的延长线于点F．求证：（1）BE•DE+AC•CE=CE2；（2）E，F，C，B四点共圆．的直径，可得∠ECB=90°．因此EF⊥BF，可得的直径，∴∠ECB=90°．∴∵EF⊥BF，∴23．（2013•哈尔滨一模）选修4﹣4：坐标系与参数方程在平面直角坐标系xOy中，直线l的参数方程为（t为参数），直线l与曲线C：（y﹣2）2﹣x2=1交于A，B两点（1）求|AB|的长；（2）在以O为极点，x轴的正半轴为极轴建立极坐标系，设点P的极坐标为，求点P到线段AB中点M的距离．24．（2013•哈尔滨一模）选修4﹣5：不等式选讲已知函数f（x）=log2（|x﹣1|+|x﹣5|﹣a）（Ⅰ）当a=5时，求函数f（x）的定义域；（Ⅱ）当函数f（x）的定义域为R时，求实数a的取值范围．）的定义域为（﹣∞，）∪（，+∞）16。

2013届宁夏银川市唐徕回民中学高三第三次模拟数学（文科）试题一、选择题（每小题5分，共60分）1．设全集+=R U ，集合A =｛02|2<-x x x ｝，B ={x }0lg≥x ，则“∈x A ”是“∈x B C U ”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．即不充分也不必要2．下面是关于复数iz +=12的四个命题 P 1：复数z 的共轭复数为i +1P 2：复数z 的实部为1 P 3：复数z 对应的向量与复数i +1对应的向量垂直 P 4：2=z其中真命题的个数为 A ．4B ．3C ．2D ．13．已知回归方程yˆ=0.85x -85.7，则该方程在样本（165，57）处的残差为 A ．54.55B ．3.45C ．2.45D ．111.554．一个简单几何体的正视图、侧视图如图所示，则其俯视图可能是①长、宽不相等的长方形 ②正方形 ③圆 ④椭圆 A ．①②B ．①④C ．②③D ．③④5．若实数x 、y 满足⎪⎩⎪⎨⎧≤≥+≤-100y y x y x ，则3x ·9y的最大值是A ．3B ．9C ．18D ．276．双曲线的一个焦点与抛物线y x 82=的焦点相同，一条渐近线与03=+-y x 平行，则该双曲线的标准方程为：A ．1322=-y x B ．12222=-y x C ．12222=-x y D ．1322=-x y7．如下图所示的算法流程图中输出的数为-55，则判断框中的条件为A ．n <11?B ．n ≥11?C ．n <10?D ．n ≥10?8．在边长为2的正方形中，有一个封闭曲线围成的阴影区域D ，现用随机模拟的方法进行了100次试验，统计出落入区域D 内的随机点共有60个，则估计区域D 的面积为 A ．512B ．53 C ．54 D ．29．已知())(sin )cos (sin 2R x x x f ∈+-+=θθθθ的图像关于y 轴对称，则θθθ2cos cos sin 2+的值为A ．23 B ．2 C ．21 D ．110．一个各条棱都相等的四面体，其外接球半径为R ，则此四面体的棱长为 A ．R 34 B ．R 27C ．R 362 D ．R 938 11．椭圆()012222>>=+b a by a x 的两个焦点是F 1，F 2，若P 是椭圆上一点，且｜PF 1｜=2｜PF 2｜，则此椭圆的离心率的取值范围是A ．[31,1)B ．（0，31） C ．（0，31] D ．（33，1） 12．已知()x f =abc x x x -+-9623)(c b a <<，且()()()0===c f b f a f ，现给出如下结论①()()010>f f ②()()010<f f ③()()030>f f ④()()030<f f ⑤4<abc⑥4>abc其中正确的结论是A ．①③⑤B ．①④⑥C ．②③⑤D ．②④⑥二、填空题（每小题5分，共20分）13．已知向量a ，b ，满足|a |=2，｜b ｜2=，且（a -b ）⊥a ，则向量a 与b 的夹角为_______.14．已知函数x x y cos sin +=，x x y cos sin 22=，则下列结论中，正确的序号是_____________.①两函数的图像均关于点（4π-，0）成中心对称；②两函数的图像均关于直线4π-=x 成轴对称；③两函数在区间（4π-，4π）上都是单调增函数； ④两函数的最小正周期相同。

2013届宁夏银川市唐徕回民中学高三第三次模拟数学（文科）试题参考答案一、选择题（每小题5分，共60分）1—5 BACBD 6—10 CCACD二、填空题（每小题5分，共20分）13．4π 14．③ 15．51 16．32 三、解答题： 17．（1）12-=n a n （2）12+=n n T n 18．（1）略 （2）63 19.（1）茎叶图12=甲x 13=乙x 8.752=甲s 42=乙s（2）由已知及（1）得：20.75=x 13y =，则a y +=x b∴ 3.8720.750.44-13=⨯=a ∴87.30.44x +=y当28=x 时，19.16=y ∴估计投中16次。

20．解：（1）因为22=e ，所以22122=-ab ，从而222b a =， 所以椭圆的方程变为122222=+by b x ，又因为椭圆经过点Q ），（221 所以1212122=+bb ，解得2,1==a b 所求椭圆方程为1222=+y x （2）由题意，过点M 的直线与椭圆交于两点，其斜率显然存在，故设其方程为 ()2-=x k y ，设()11,y x A ，()22,y x B ，()00,y x P由()⎪⎩⎪⎨⎧=+-=12222y x x k y 得()0222222=--+x k x ，即()028*******=-+-+k x k x k 由()()028********>-+-=∆k k k ，解得212<k 222122212128,218k k x x k k x x +-=+=+，()221212144kk x x k y y +-=-+=+ 因为OP OB OA t =+，所以021tx x x =+，021ty y y =+，由因为t ty tx =+00，所以t k k k k =+-+222214218 即124442148222++-=+-=k k k k k t ()()()()62462444131244314121442-=--≥-+++-=++-++-=k k k k k当且仅当⎪⎪⎭⎫ ⎝⎛-∈⎪⎪⎭⎫ ⎝⎛-=22,22126k 时62min -=t或者对函数124442++-=k k t 求导也可以。

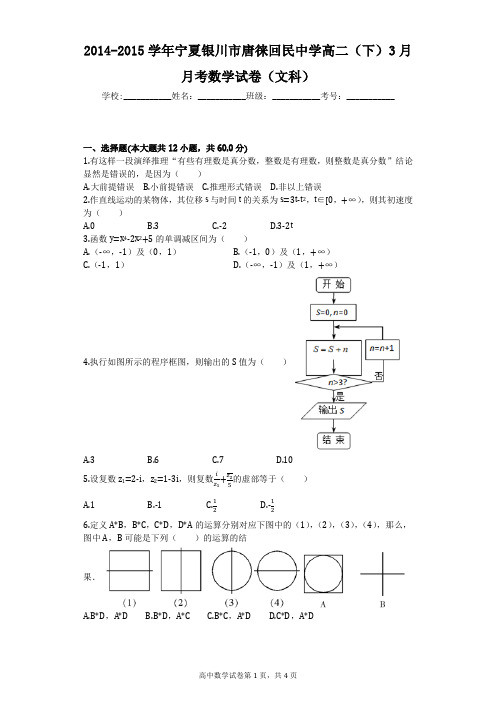
2014-2015学年宁夏银川市唐徕回民中学高二（下）3月月考数学试卷（文科）学校:___________姓名：___________班级：___________考号：___________一、选择题(本大题共12小题，共60.0分)1.有这样一段演绎推理“有些有理数是真分数，整数是有理数，则整数是真分数”结论显然是错误的，是因为（）A.大前提错误B.小前提错误C.推理形式错误D.非以上错误2.作直线运动的某物体，其位移s与时间t的关系为s=3t-t2，t∈[0，+∞），则其初速度为（）A.0B.3C.-2D.3-2t3.函数y=x4-2x2+5的单调减区间为（）A.（-∞，-1）及（0，1）B.（-1，0）及（1，+∞）C.（-1，1）D.（-∞，-1）及（1，+∞）4.执行如图所示的程序框图，则输出的S值为（）A.3B.6C.7D.105.设复数z1=2-i，z2=1-3i，则复数+的虚部等于（）A.1B.-1C.D.-6.定义A*B，B*C，C*D，D*A的运算分别对应下图中的（1），（2），（3），（4），那么，图中A，B可能是下列（）的运算的结果．A.B*D，A*DB.B*D，A*CC.B*C，A*DD.C*D，A*D7.某公司要在某一规划区域内筹建工厂，拆迁与工程设计可同时进行，如果工程设计分为土建设计与设备采购两个部分，两者可同时进行；拆迁和土建设计进行完才能进行厂房建设，厂房建设和设备采购进行完才能进行设备安装调试，最后才能进行试生产．上述过程的工序流程图如图．则设备采购，厂房建设，土建设计，设备安装与图中①②③④处正确的对应次序应为（）A.①②③④B.①④②③C.②③①④D.①③②④8.利用独立性检验来考虑两个分类变量X和Y是否有关系时，通过查阅下表来确定断言“X和Y有关系”的可信度，如果k＞5.024，那么就有把握认为“X和Y有关系”的百A.25%B.75%C.2.5%D.97.5%9.已知函数f（x）=ax3-x2+x-5在（-∞，+∞）上既有极大值，也有极小值，则实数a 的取值范围为（）A.a＞B.a≥C.a＜且a≠0D.a≤且a≠010.如果圆柱的轴截面周长为定值4，则圆柱体积的最大值为（）A.πB.πC.πD.π11.函数f（x）=lnx-x2的极值情况为（）A.无极值B.有极小值，无极大值C.有极大值，无极小值D.不确定12.某考察团对全国10大城市进行职工人均工资水平x（千元）与居民人均消费水平y （千元）统计调查发现，y与x具有相关关系，回归方程为=0.66x+1.562．若某城市居民人均消费水平为7.675（千元），估计该城市人均消费额占人均工资收入的百分比约为（）A.83%B.72%C.67%D.66%二、填空题(本大题共4小题，共20.0分)13.在平面直角坐标系x O y中，点P在曲线C：y=x3-10x+3上，且在第二象限内，已知曲线C在点P处的切线斜率为2，则点P的坐标为______ ．14.若a1，a2，a3，a4∈R+，有以下不等式成立：，，．由此推测成立的不等式是______ ．（要注明成立的条件）15.在同一坐标系中，将曲线4x2+9y2=36变为曲线x′2+y′2=1的伸缩变换是______ ．16.已知函数f（x）=-x3+ax在区间（-1，1）上是增函数，则实数a的取值范围是______ ．三、解答题(本大题共6小题，共70.0分)17.已知复数z1满足（z1-2）（1+i）=1-i（i为虚数单位），复数z2的虚部为2，且z1•z2是实数，求z2．18.已知x∈R，a=x2-1，b=2x+2．求证a，b中至少有一个不小于0．19.（1）求直线与圆ρ=2ccosθ（c＞0）相切的条件；（2）求曲线θ=0，和ρ=4所围成图形的面积．20.在2013年春节期间，某市物价部门，对本市五个商场销售的某商品一天的销售量及其价格进行调查，五个商场的售价x元和销售量y件之间的一组数据如下表所示：通过分析，发现销售量y对商品的价格x具有线性相关关系．（1）求销售量y对商品的价格x的回归直线方程；（2）欲使销售量为12，则价格应定为多少．附：在回归直线中，=-．21.若函数f（x）=ax3-bx+4，当x=2时，函数f（x）有极值为，（Ⅰ）求函数f（x）的解析式；（Ⅱ）若f（x）=k有3个解，求实数k的取值范围．22.已知函数f（x）=x2+lnx．（1）求函数f（x）在[1，e]上的最大值和最小值；（2）求证：当x∈（1，+∞）时，函数f（x）的图象在g（x）=x3+x2的下方．。

银川唐徕回民中学2015～2016学年度第二学期高三年级第三次模拟考试数学试卷（文科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第22～24题为选考题，其它题为必考题。

考生作答时，将答案答在答题卡上，在本试卷上答题无效。

考试结束后，将本试卷和答题卡一并交回。

注意事项：1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。

2．选择题答案使用2B 铅笔填涂,如需改动，用橡皮擦干净后，再选涂其他答案的标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。

3．请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。

4．保持卡面清洁，不折叠，不破损。

5．做选考题时，考生按照题目要求作答，并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。

第I 卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的．1．集合{}Zn x x A n∈==,2，}{3,2,1=B ，则B A ⋂的子集的个数为（ ）A. 2B. 3C. 4D. 82. i 为虚数单位，复数1-i i在复平面内对应的点到原点的距离为（ ）B. 1C.2D.123．下列函数中，既是偶函数，又在（0，∞+）上是单调减函数的是（ ） A ．12yx =B ．2xy =-C ．ln 1y x =+D ．cos yx =4．某工厂对一批产品进行了抽样检测。

右下图是根据抽样检测后的产品净重（单位：克）数 据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100)，[100，102)，[102，104)，[104，106]. 已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是（ ） A. 90 B. 75C. 60D. 455．下列说法正确的是（ ）A ．命题“R x ∈∃使得0322<++x x ”的否定是：“032,2>++∈∀x x R x ” B ．命题p ：“2cos sin ,≤+∈∀x x R x ”， 则⌝p 是真命题C ．“p q ∧为真命题”是“q p ∨为真命题”的必要不充分条件D ．“1<a ”是“0log 21>a ”的必要不充分条件6．在正项等比数列{}n a 中，369lg lg lg 6a a a ++=，则111a a 的值是（ ） A. 10B. 1000C. 100D. 100007. 在空间直角坐标系xyzo -中，一个四面体的顶点坐标分别是（0，0，2），（2，2，0），（1，2，1），（2，2，2），给出编号①、②、③、④的四个图，以yOz 平面为正视图的投影面，则该四面体的正视图和俯视图分别为（ ）A ．①和②B ．③和①C ．③和④D ．④和②8．将函数)64(sin 3(π+=x x f ）图象上所有点的横坐标伸长到原来的2倍，再向右平移6π个单位长度，得到函数)(x g y =的图象．则)(x g y =图象的一条对称轴是（ ） A ．x ＝12πB ．x ＝6πC ．x ＝3πD ．x ＝23π 9．执行如右图所示的程序框图,如果输出3s =,那么判断 框内应填入的条件是（ ） A ．6k ≤ B ．7k ≤ C ．8k ≤D ．9k ≤10．已知y x z c y x y x x y x +=⎪⎩⎪⎨⎧≥++-≤+≥302,42,且目标函数满足的最小值 是5，则z 的最大值是（ ）A ．10B ．12C ．14D ．1511．已知双曲线122=-my x 与抛物线x y 82=的一个交点为P ，F 为抛物线的焦点，若5=PF ，则双曲线的渐近线方程为（ ）A ．03=±y xB ．03=±y xC ．02=±y xD ．02=±y x12．已知函数⎪⎩⎪⎨⎧-=-xx ee xx f )( ）（0)0(<≥x x ， 若函数)1()(+-=x k x f y 有三个零点，则实数k 的取值范围为（ ）A.)0,21(- B ．1(0,)2 C. 1(,1)2D. (1,)+∞第Ⅱ卷本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第24题为选考题，考生根据要求做答．二、填空题：( 本大题共4小题，每小题5分 )13. =︒︒+︒︒313sin 1333sin 943sin 523sin ________.14. 在ABC ∆中，已知90,3,4ACB CA CB ∠===，点E 是边AB 的中点，则CE AB ⋅= .·15. 已知直三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若34AB AC ==，, AB AC ⊥,112AA =,则球O 的表面积为________.16．如图，为了测量A 、C 两点间的距离，选取同一平面上B 、D 两点，测出四边形ABCD各边的长度（单位：km ）：5=AB ，8=BC ，3=CD ，5=DA ，且B ∠与D ∠互补，则AC 的长为_____km .三、解答题: ( 解答应写出文字说明．证明过程或演算步骤 )17．（本小题满分12分）已知在递增等差数列{}n a 中，12a =，3a 是1a 和9a 的等比中项． （Ⅰ）求数列{}n a 的通项公式； （Ⅱ）若()1+1n nb n a =，n S 为数列{}n b 的前n 项和，当n S m <对于任意的+n ∈N 恒成立时，求实数m 的取值范围.18.（本小题满分12分）某花店每天以每枝6元的价格从农场购进若干枝玫瑰花，然后以每枝12元的价格出售。

宁夏银川市唐徕回民中学2015届高三8月月考化学试题第I 卷（选择题，共40分）一、选择题（选出下列各小题中唯一符合题意．．．．．．的答案，每小题2分，共40分。

） 1.下列物质中，属于电解质的是： A.CO 2B.盐酸C.BaSO 4D.C 2H 5OH2.某些化学概念在逻辑上存在下图所示关系，则下列说法中正确的是：A.纯净物(B)与混合物(A)属于包含关系B.化合物(B)与氧化物(A)属于包含关系C.单质与化合物属于交叉关系D.氧化反应与化合反应属于并列关系3.利用右图装置(瓶口向上)不可行．．．的实验是： A.A 口进气，B 口排气，用于收集H 2 B.广口瓶充满水，从A 中进气用于收集O 2C.广口瓶中盛有浓硫酸，从B 口进气用于干燥SO 2气体D.广口瓶盛有NaOH 水溶液，从B 中进气用于除去Cl 2中的HCl 气体4.用98%的浓H 2SO 4配制1.0mol/L 的稀H 2SO 4时，某同学经量取、稀释、转移、洗涤、定容后(每 步操作均准确)，发现容量瓶内溶液的温度高于室温，则所配的溶液浓度与1.0mol/L 相比: A.偏大 B.偏小 C.相等 D.无法确定5.下列叙述正确的是:A.因为NH 3·H 2O 是弱碱，所以不能用氨水与FeCl 3溶液反应制取Fe(OH)3B.向FeI 2溶液中通入少量Cl 2，再滴加少量CCl 4，振荡、静置，下层液体为紫色C.向一定体积的热浓硫酸中加入过量的铁粉，生成的气体能被烧碱溶液完全吸收D.将SO 2气体通入溴水，欲检验溶液中是否有SO 2－4生成，可向溶液中滴加Ba(NO 3)2溶液 6.丰富多彩的颜色变化增添了化学实验的魅力，下列有关反应颜色变化的叙述中正确的是: ①新制氯水久置→黄绿色消失 ②淀粉溶液遇碘单质→蓝色 ③蔗糖中加浓硫酸搅拌→白色 ④SO 2通入品红溶液中→红色褪去 ⑤氨气通入酚酞溶液中→红色 A.①②③④ B .①②④⑤C .②③④⑤D.全部7.下列有关实验操作的说法正确的是：A.可用25mL 碱式滴定管量取20.00mL KMnO 4溶液B.用pH 试纸测定溶液的pH 时，需先用蒸馏水润湿试纸C.蒸馏时蒸馏烧瓶中液体的体积不能超过容积的2/3，液体也不能蒸干D.将金属钠在研钵中研成粉末，使钠与水反应的实验更安全8.如图所示装置中，干燥烧瓶内盛有某种气体，烧杯和滴管内盛放某种溶液。

高三8月月考数学（文）试题一、选择题（本大题包括12小题，每小题5分，共60分，每小题给出的四个选项中，只有一项．．．．是符合题目要求的，请将正确选项填涂在答题卡上）1. 已知集合U={1,2,3,4,5,6}，A={1，4，5}，B={2，3，4}，则()=B C A U U ( )A.{4}B. {1，5}C.{1，5，6}D.{1，4，5，6}2. 已知命题;1tan ,:=∈∃x R x p 命题,01,:2>+-∈∀x x R x q 则下列命题中是假命题的是（ ）A.q p ∧B.q p ∨C.q p ⌝∧D.q p ⌝∨3. 已知函数⎩⎨⎧>≤+=)0(2)0(3)(x x x x f x ，则))2((-f f 的值为（ ）A.4B.41C.-1D.24. 函数24)1ln(1)(x x x f -++=的定义域为（ ）A.]2,0()0,2[U -B.]2,0()0,1(U -C.[-2,2]D.]2,1(- 5. 下列函数中，既是偶函数又是在),0(+∞上单调函数的是（ ） A.3x y =B.x y cos =C.21xy =D.x y ln = 6. 设函数)(x f 定义在实数集上，)()2(x f x f =-，且1≥x 当时，x x f ln )(=，则有（ ）A. )21()2()31(f f f << B. )31()2()21(f f f <<C. )2()31()21(f f f <<D. )31()21()2(f f f <<7. 已知函数))(()(b x a x x f --=（其中b a >）的图象如图所示，则函数b a x g x+=)(的图象是（ ）8. 已知函数x x g )31()(=与函数)(x f y =的图象关于直线x y =对称，若)2.0(g a =，)2.0(),2(f c f b ==，则( )A.c b a <<B.c a b <<C.b c a <<D.a b c << 9. 定义在R 上的偶函数)(x f 在),0[+∞上递增，0)31(=f ，则满足0)(log 81>xf 的x 取值范围是（ ）A. ),0(+∞B. ),2()21,0(+∞UC. )2,21()81,0(UD. )21,0( 10. 曲线3x y =在点（3,27）处的切线与两坐标轴所围成的三角形面积是（ ）A. 53B. 54C. 35D. 4511. 已知定义在R 上的函数)(x f 满足：13)2()(=+⋅x f x f ，若,2)1(=f ，则=)2011(f （ ）A. 2B.21 C. 13 D. 213 12. 若函数))((R x x f y ∈=满足)()2(x f x f =+，且]1,1[-∈x 时，21)(x x f -=，函数⎪⎩⎪⎨⎧<->=)0(1)0(lg )(x xx x x g ，则函数)()()(x g x f x h -=在[]5,5-上的零点个数为（ ） A. 5 B. 7 C. 8D. 10本卷包括必考题和选考题两部分。

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集{}2250,M x x x x Z =+<∈,集合{}0,N a =, 若MN ≠Φ，则a 等于（ ）A. 1-B. 2C. 1-或2D. 1-或2-2．已知命题x x R x p lg 2,:>-∈∃，命题0,:2>∈∀x R x q ，则( ) A. 命题q p ∨是假命题 B. 命题q p ∧是真命题 C. 命题)(q p ⌝∧是真命题D. 命题)(q p ⌝∨是假命题3. 已知α∈（2π,π），sin α=53,则tan （4πα-）等于（ ）A ． －7B ． － 71C ． 7D ．714. 在△ABC 中，若222sin sin sin A B C +<，则△ABC 的形状是（ ） A ．钝角三角形B. 直角三角形C. 锐角三角形D. 不能确定5．若曲线y=2x ax b ++在点（0.b ）处的切线方程式1x y -+=0，则（ ） A. 1a =，1b = B. 1a =-，1b = C. 1a =，1b =-D. 1a =-1b =-6.ABC ∆的内角C B A ,,的对边分别为c b a ,,已知,4,6,2ππ===C B b 则ABC ∆的面积为（ ）A ．23＋2 B.3＋1 C ．23－2 D.3－17. 执行如图所示的程序框图，则输出的k 的值是( )A ． 3B ．4C ．5D ．68. 若平面四边形ABCD 满足0,()0,AB CD AB AD AC +=-⋅= 则该四边形一定是( )A. 直角梯形B. 矩形C. 菱形D. 正方形 9. 已知函数)(x f 为奇函数，且当0>x 时，,1)(2xx x f +=则)1(-f 等于( )A ．2B ．1C ．0D ．2-10.函数13y x x =-的图象大致为11. 已知函数),(,1)(22R b a b b ax x x f ∈+-++-=,对任意实数x 都有)1()1(x f x f +=-成立,若当[]1,1-∈x 时,0)(>x f 恒成立,则b 的取值范围是( )A ．01<<-bB ．12-<>b b 或C ． 2>bD ．1-<b12. 若存在正数x 使1)(2<-a x x 成立，则a 的取值范围是( )A ．(－∞，＋∞)B ． (－1，＋∞)C ．(0，＋∞)D ． (－2，＋∞)二、填空题（本大题共4小题，每小题5分，共20分．）13．已知数列1,,9a 是等比数列，数列121,,,9b b 是等差数列，则12a b b +的值为 .14．已知向量)sin ,(cos a θθ=→,向量)1,3(b -=→则|b a 2|→→-的最大值是 _____ 15．若函数a x x x f +-=23)(在[]1,1-的最小值是1，则实数a 的值是.16. 给出如下五个结论：①存在)2,0(πα∈使31cos sin =+a a ②存在区间（,a b ）使x y cos =为减函数而x sin ＜0 ③x y tan =在其定义域内为增函数④)2sin(2cos x x y -+=π既有最大、最小值，又是偶函数⑤) ⎝⎛+=62sin πx y 最小正周期为π其中正确结论的序号是三、解答题：本大题共6小题，共70分。

银川唐徕回民中学2014～2015学年度第二学期第三次模拟考试高三年级数学试卷（理科）一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的．1．已知集合A ＝{x ∈R| |x|≤2 }，B ＝{x ∈R|x≤1}，则A ∩B 等于( ) A ．(－∞，2] B ． C ． D ．2. 如图，在复平面内，复数12,Z Z 对应的向量分别是,,OA OB u u u r u u u r则12||Z Z +=（ ）A ．2B.3C.22D. 333．已知双曲线 22221(0,0)x y a b a b -=>>的一条渐近线方程是 3y x =，它的一个焦点在抛物线248y x =的准线上，则双曲线的方程为（ ） A ．22110836x y -= B ．221927x y -= C ．22136108x y -= D ．221279x y -=4. 已知向量)3sin(,),3cos ,1(),1),6(sin(πααπα+⊥-=+=则若b a b a 等于（ ）A ．1B ．-1C ．3D ．-35. 已知直线1y x =+与曲线ln()y x a =+相切，则a 的值为（ ） A ．1B. 2C. 1-D. 2-6． 设不等式组220x y x y y ⎧+≤⎪⎪-≥-⎨⎪≥⎪⎩所表示的区域为M ，函数21y x -x 轴所围成的区域为N ,向M 内随机投一个点,则该点落在N 内的概率为（ ）A. 2πB. 4πC.8πD. 16π7. 下列说法正确的是（ ）A. “0x <”是“ln(1)0x +<”的充要条件B. “2x ∀≥，2320x x -+≥”的否定是“2,x ∃<2320x x -+<”C. 采用系统抽样法从某班按学号抽取5名同学参加活动，学号为5,16,27,38,49的同学均被选出，则该班学生人数可能为60D. 在某项测量中，测量结果X 服从正态分布2(1,)(0)N σσ>，若X 在(0,1)内取值的概率为0.4，则X 在(0,2)内取值的概率为0.88．函数()()sin 002f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭其中，， 的图象如图所示，为了得到()sin 2g x x=的图象，则只需将()f x 的图象( )A ．向左平移6π个长度单位B ．向右平移3π个长度单位 C ．向右平移6π个长度单位 D ．向左平移3π个长度单位9． 执行如图所示的程序框图，如果输出s ＝3，那么判断框内应填入的条件是( ) A ．k≤6 B ．k≤7 C ．k≤8 D ．k≤9 10. 一个四面体的四个顶点在空间直角坐标系xyz O -中的坐标分别是（0，0，0）， （1，2，0），（0，2，2），（3，0，1），则该四面体中以yOz 平面为投影面的 正视图的面积为（ ）A ．3B ．25C ．2D ．2711．过点（1，1）的直线与圆224640x y x y +--+=相交于A ，B 两点， 则|AB|的最小值为（ ） A. 23 B.4C. 25D. 512. 已知函数，，，⎪⎩⎪⎨⎧>+-≤<=10621100|lg |)(x x x x x f 若函数92)(2)(2-+-=b x bf x f y 有6个零点，则b 的取值范围是（ ）A ．⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛31,9297,32Y B ．⎪⎭⎫ ⎝⎛∞-⎪⎭⎫ ⎝⎛+∞31,,32YC ．⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛1,3231,0Y D ．⎪⎭⎫ ⎝⎛97,92二、填空题：本大题共4小题，每小题5分．13. 平面向量a ρ与b ρ的夹角为60°，a ρ=(2,0)，|b r |=1，则|a ρ+2b ρ|＝14. 设212a xdx =⎰，则61ax x ⎛⎫- ⎪⎝⎭的展开式中常数项为 15. △ABC 的三个顶点在以O 为球心的球面上，且cos 3A =，BC=1，AC=3，三棱锥O- ABC的体积为6，则球O 的表面积为__________。

银川唐徕回民中学2014～2015学年度第三次模拟考试高三年级文科综合试卷命题：高三文科备课组第Ⅰ卷(选择题，140分)本卷共35个小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

读表1，完成1～2题。

注：产业结构偏离度是指各产业的增加值比重与就业比重之比同1的差。

1．根据信息，可以判定（）A．产业结构偏离度与产业增加值比重成正相关B．产业结构偏离度与产业就业比重成负相关C．产业结构偏离度为负值,表明该产业的产值高，吸引了大量劳动力D．产业结构偏离度为正值,表明该产业还具有一定的劳动力吸纳优势2．据表1信息推测该市2012年以后一段时间内（）A．工业化将会继续推动城市化发展B．第三产业发展快速，吸引大量劳动力C．农业生产受到限制，产值将下降D．劳动力过剩，人口向外流动读印度尼西亚的巴厘岛示意图（图1），完成3～5题。

图13．关于该岛屿叙述正确的是（）①最大山脉大致为东西走向②南部比北部坡度缓③河流含沙量比较大④7月受西北风影响A．①②B．①④ C．②③ D．③④4．巴厘岛东、西部存在区域差异，稻田主要分布在该岛东部，其原因最可能是（）A．东部地区地形平坦B．西部水热条件不如东部优越C．东部有肥沃的火山灰土D．东部地广人稀，利于机械化生产5．下列巴厘岛经济发展的各项措施中，最可行的是（）A．大力发展水稻种植，出口创汇B．大力发展旅游业，带动相关产业图2C ．大面积种植热带经济作物，改善环境D ．大力兴建沿海港口，收取过往费用 红树林是生长在热带、亚热带地区海岸潮间带滩涂上的森林。

读某大洲红树林分布和该大洲某岛等高线图（图2），回答6～7题。

6. 该大洲红树林东西两岸纬度分布出现差异的最主要因素是（ ）A.光照B.地形C. 大气环流D. 洋流7. 该岛甲、乙、丙、丁四地中降水最多的是A.甲地B.乙地C.丙地D.丁地转场是指山区牧民为了获得优质牧草，随着季节的变化将牲畜赶往不同牧场的现象。