当前位置：文档之家 › 第五章：旋涡理论

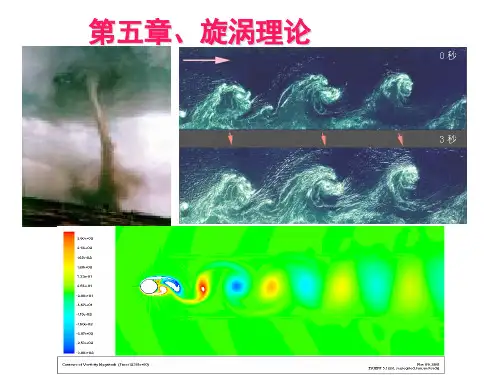
第五章：旋涡理论

  • 格式：pdf
  • 大小：184.76 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

第五章漩涡理论基础

第五章漩涡理论基础

第五章不可压缩流体的二维流动引言：在前面几章主要讨论了理想流体和黏性流体一维流动，为解决工程实际中存在的一维流动问题打下了良好的基础。

本章讨论理想不可压流体的二维有势流动以及二维黏性流体绕物体流动的基本概念。

第一节有旋流动和无旋流动刚体的运动可分解为移动和转动两种运动形式，流体具有移动和转动两种运动形式。

另外，由于流体具有流动性，它还具有与刚体不同的另外一种运动形式，即变形运动(deformationmotion)。

本节只介绍流体旋转运动即有旋流动(rotation—alflow)和无旋流动(irrotational flow)。

一、有旋流动和无旋流动的定义流体的流动是有旋还是无旋，是由流体微团本身是否旋转来决定的。

流体在流动中，如果流场中有若干处流体微团具有绕通过其自身轴线的旋转运动，则称为有旋流动，如果在整个流场中各处的流体微团均不绕自身轴线的旋转运动，则称为无旋流动。

强调“判断流体流动是有旋流动还是无旋流动，仅仅由流体微团本身是否绕自身轴线的旋转运动来决定，而与流体微团的运动轨迹无关。

”举例虽然流体微团运动轨迹是圆形，但由于微团本身不旋转，故它是无旋流动；在图5—1(b)中，虽然流体微团运动轨迹是直线，但微团绕自身轴线旋转，故它是有旋流动。

在日常生活中也有类似的例子，例如儿童玩的活动转椅，当转轮绕水平轴旋转时，每个儿童坐的椅子都绕水平轴作圆周运动，但是每个儿童始终是头向上，脸朝着一个方向，即儿童对地来说没有旋转。

二、旋转角速度(rotationalangularvelocity)为了简化讨论，先分析流体微团的平面运动。

如图5—2所示有一矩形流体微团ABCD在XOY平面内，经丛时间后沿一条流线运动到另一位置，微团变形成A，B，C，D。

流体微团在Z周的旋转角速度定义为流体微团在XOY平面上的旋转角速度的平均值速度环量是一个标量，但具有正负号。

速度环量的正负号与速度方向和积分时所取的绕行方向有关。

第五章 漩涡理论

第五章 漩涡理论

第五章 漩涡理论内容1. 基本概念。

2. 漩涡随空间，时间的变化规律。

3. 漩涡对周围流场的影响。

4. 二元漩涡的特性。

5.1.1涡量和平均旋转角速度。

涡量场：Ω =▽V ⨯▽V ⨯=VzVyVxz y x k j i ∂∂∂∂∂∂令 ωx =⎪⎪⎭⎫⎝⎛∂∂-∂∂z Vy yVz 21 ⎪⎭⎫ ⎝⎛∂∂-∂∂=x Vz zVxy 21ω ω2=Ω∴ ⎪⎪⎭⎫⎝⎛∂∂-∂∂=y Vx xVy z 21ω其中ω称为平均旋转角速度。

ωωωzyx,, 的物理意义。

设M 点的速度Vx,Vy A 点()dx xVx x VV xA∂∂+=()dx xVy y VV yA∂∂+=()()[]()[]11_sin 0,11dtx dtx dtx dt dtx dxy A A MA d V V V VV VV AA y dt x y xAyA⎪⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂=+-='+==→θ dt xd V y∂∂≈∴θ1 即xV dtd y∂∂=θ1Ω是否为0判断有旋无旋例：1）r V∙=ωθ=ω常sin sin cos 0012xy z xyyxzr yrcso xV V V V VV V yx θθθωθωθωθωωωωω=-=-=-======⎛⎫⎪=-= ⎪⎝⎭∂∂∂∂有旋2）rV πθ2Γ=无旋02100222222=⎪⎪⎪⎭⎫⎝⎛-===∴=+Γ=+Γ-=∴∂∂∂∂yV x V VyxV yxVxyzyx zyxx yωωωππ5.1.2涡线，涡面和涡管涡线：是一条曲线，在同一瞬时曲线上所有点旋转角速度Ω与该线相切。

1. 瞬时性2. 流动速度与旋转速度相垂直。

涡线方程()()()z y x dzz y x dyz y x dxz y x ,,,,,,ΩΩΩ==涡线涡管速度场 涡量场 Ω=⨯∇v 流线：zyxv dz v dy v dx == 涡线：zyxdz dy dx Ω=Ω=Ω流管： 涡管：流量：⎰=sn ds v Q 涡量：⎰⎰⎰==Γ=sn CC s ndsl d v dsJ ωω25.1.3涡通量和涡管强度⎰⎰=∙=ssnds ds n J ωω又称涡管强度流量⎰⎰=∙=ssnds ds n v Q v5.2速度环流和斯托克斯定理1）速度环流：定义：速度在曲线切线上的分量沿该曲线的线积分⎰Γ=BAABl d V定义：某瞬时AB 线上所有质点沿AB 运动的趋势。

漩涡理论

漩涡理论

由涡丝引起的速度称为旋涡诱导速度场。
无限长的直涡丝 点涡的诱导速度
点涡
v
2 R
vr 0 （R为场点至点涡的距离）
这种速度场是无旋的
！！点涡不对自身 产生诱导速度
R
• 举例：
设涡线位于原点，根据斯托克斯定理，沿以r为半
径的圆周的速度环量等于该圆周内的涡通量，当涡 线的涡度不变时，沿任意圆周的速度环量Γ为常数， 称Γ为涡线的强度（逆时针为正）
同瞬时的旋转角速度矢量 r
同瞬时的流速矢量
r
r v
与此线
与此线相切。 r3
r 2
相切。
v3 r v2
r
r1
v1
涡线微分方程：
取涡线上一段微弧长
dsr
r dxi
r dyj
r dzk
该处的旋转角速度
r
r
xi
y
r j
r
z k
涡矢量与涡线相切
x
(
dx x, y,
z,
t)
y
ห้องสมุดไป่ตู้
(
dy x, y,
z,
t)
z
dz (x, y,
旋涡理论(vortex theory) 旋涡场的基本概念（涡线，涡管，旋涡强度）
园盘绕流尾流场中的旋涡
圆球绕流尾流场中的旋涡
圆柱绕流尾流场中的旋涡
有攻角机翼绕流尾流场中的旋涡
一、涡线,涡管,旋涡强度 涡线(vortex line)： 流线(streamline)：
涡线上所有流体质点在 流线上所有流体质点在
涡管vortex tube
流管
涡丝vortex filament
截面积为无限小的涡束 称为涡索（涡丝）。
流体力学教案第5章流体漩涡运动基础

流体力学教案第5章流体漩涡运动基础

第五章 流体旋涡运动基础§5-1 旋涡运动的几个基本概念一、涡量场对有旋流动，0≠ω ，而),,,(t z y x f ＝ω，所以对有旋流动的流场中同时存在一个旋涡场，或称涡量场或角速度场。

k Ωj Ωi ΩΩz y x++= (1)zy w Ωx ∂∂-∂∂=υ xwz u Ωy ∂∂-∂∂=(2) yu x Ωz ∂∂-∂∂=υ 满足涡量连续性方程：0=∂∂+∂∂+∂∂zΩy Ωx Ωzy x (3) 二、涡线同速度场中引进流线、流管和流量的定义一样。

下面我们定义涡线、涡管、涡束以及旋涡强度(涡通量)。

涡线――涡线是旋涡场中的一条曲线，在某一瞬时，曲线上各点的切线方向与该点流体微团的角速度ω方向重合。

(Ω 方向的判别，根据右手螺旋法则)对非定常流动涡线的形状随时间而变，对定常流动，涡线形状不随时间而变。

与流线一样，涡线本身也不会相交。

取k z j y i x sd d d d ++=为涡线上一微元线段。

类似于流线微分方程，或由0d d d d ==⨯zyx ΩΩΩk j is Ωz y x可得到涡线微分方程为：),,,(d ),,,(d ),,,(d t z y x Ωzt z y x Ωy t z y x Ωx z y x == (4)三、涡管和涡束涡管－在涡量场中任取一不是涡线的封闭曲线，通过封闭曲线上每点的涡线，这些涡线形成一管状表面，称为涡管。

涡束－涡管中充满作旋转运动的流体，称为涡束。

四、涡通量涡通量－通过任一开口曲面的涡量的总和。

通过开口曲面A 涡通量为：A n ΩJ Ad ⎰⎰⋅=n为d A 的外法线单位向量 对于封闭曲面：A n ΩJ Ad ⎰⎰⋅=由于：0=∂∂+∂∂+∂∂zΩy Ωx Ωzy x 所以：0d =⋅=⎰⎰A n ΩJ A五、速度环量定义如下：在流场中任取一通曲线AB 。

AB 曲线上任一点的速度为V，在该点B 附近的曲线上任取一微元线段s d ，V 与sd 的夹角为α。

流体力学--漩涡理论 ppt课件

流体力学--漩涡理论 ppt课件

17
2 有限平面
C 2 n d 2 J

（单连通区域）
单连通区域： C 所包围的区域σ 内全部是流
体，没有固体或空洞。
3 任面
PPT课件
C
18
复连通域(多连通域)：
C的内部有空洞或者包 含其他的物体。 双连通域的斯托克斯定理
ABDB ' A' EA AB C BA L
该处的速度
v vx i v y j vz k
流速与流线相切
dx dy dz vx ( x, y, z, t ) vy ( x, y, z, t ) vz ( x, y, z, t )
v
ds
PPT课件
ds
8
涡管vortex tube
流管
元流 截面积为无限小的涡束 截面积为无限小的流束 称为元流 称为涡索（涡丝）。 PPT课件 9
AB Vx dx Vy dy Vz dz dx dy dz x y z AB AB
B
d B A
A
V
Vs
B
对于有旋场:
AB V ds Vx dx Vy dy Vz dz
AB AB
PPT课件
Ｂˊ Ａˊ Ｂ Ａ
σ
C
Ｌ
Ｅ
AB BA
C L 2 n d

C
区域在走向的左侧
PPT课件 19
漩涡理论
推论一 单连域内的无旋运动，流场中处处 为零，则沿任意封闭周线的速度环量为 零
c 2 n d 2 0d 0

沿某闭周线的速度环量为零，不一定无旋。
vx ( )dxdy x y vy
旋涡理论

旋涡理论


(r

a2 r
)


2

vr


r
V0
cos (1
a2 r2
)

v

1 r


V0 sin (1
a2 r2
)


2
r

柱面上(r = a):
v

vr 0
2V0 sin




2 a
v 0
sin 4 aV0
6.1.4 点涡 (vortex)
流场中坐标原点处有一根无穷长的直涡线，方向垂直
于图平面，则该涡线与图平面的交点即为一个点涡。
位于（0，0）点涡：
vr
0，
v


2 r

vr dr
v rd



2


v dr

vr rd


2
ln
r
v

Γ顺时针方向，若逆时针，上式加负号。
第5章 旋涡理论
内容：介绍描述旋涡运动的基本方法和旋涡运动的
基本定理。
包括：（1）旋涡运动的基本概念。
（2）旋涡运动的基本定理。 汤姆逊（Thomson）定理 拉格朗日（Lagrange）定理 亥姆霍兹（Helmholtz）定理 毕奥沙伐（Biot——Savart）定理
4
1、涡线：流场中的一条曲线。 其上所有流体
d

J：表征流场中旋涡的强弱和分布面积大小的物理量。
4 、旋速度环量：
C C vsds C v cosds C v ds
流体力学5-漩涡理论说课材料

流体力学5-漩涡理论说课材料


(vy vx )dxdy x y
y
d
vx
vx y
dy
c
而
(vy x
vx y
)
2z
微矩形面积ds上的环量：
v y dy
av x
0
dx
vy
vy x
dx
b x
d 2zd S 2n d S 2 d J
漩涡理论
2 有限平面
C 2nd2J （单连通区域）
单连通区域： C 所包围的区域σ内全部是流
ds
A BV d sV xd x V yd y V zd z
A B
A B
A
漩涡理论
2. 若已知速度场，求沿一条闭曲线的速度环量
对于无旋场:
c cVxdx Vydy Vzdz
c x dx y dy z dz c d 0
对于有旋场:
V
α Vs
ds C
c cVsds2nd
————斯托克斯定理
即涡管永远由相同的流体质点所组成。 但涡管的形状和位置可能随时间变化。
涡管
涡管
漩涡理论
海姆霍兹第三定理 ——涡管旋涡强度不随时间而变
正压、理想流体在有势质量力作用下，涡管 的旋涡强度不随时间而变。
2 J (斯 托 克 斯 定 理 ）
不 随 时 间 变 化 （ 汤 姆 逊 定 理 ）
J不 随 时 间 变 化
定义 AB ABVsds
速度环量是标量，速度方向与
积分AB曲线方向相同时（成锐 角）为正,反之为负。
ΓAB＝－ΓBA
A
V
Vs
B
ds
漩涡理论
速度环量的其他表示形式：
AB V ds
第05章__漩涡理论

第05章__漩涡理论

39
海姆霍兹第一定理既适用于理想流体又适用于 粘性流体。
海姆霍兹第二、三定理只适用于理想流体。
因为流体的粘性将导致剪切、速度等 参数脉动以及能量耗散，旋涡强度将随时 间衰减。
40
§5-4 毕奥一沙伐尔定理
问题 已知速度场可由式（3-39）和（3-40）
求偏导来确定旋涡场。
已知旋涡场，能否确定速度场？这是本节 要讨论的问题．
诱导速度场
涡丝(线)
旋涡强度
诱导速度场 dV
42
电磁场与诱导速度场的类比
dH
i
ds sin r2
场点 43
电磁学中，电流强度为ｉ的导线，微元导
线ds对场点Ｐ所产生的磁场强度由毕奥——沙
伐尔公式得:
dH i ds sin
式中：
r2
ｒ: ds离场点P的矢径
θ: 是ds与ｒ的夹角
dH的方向:
垂直于ds和ｒ所在的平面，按右手法则确定。
15
旋涡运动理论广泛地应用于工程实际: 机翼、 螺旋桨理论等。旋涡与船体的阻力、振动、噪 声等问题密切相关。
旋涡的产生： 与压力差、质量力和粘性力等
因素有关。
流体流过固体壁面时，除壁面附近粘性影响严 重的一薄层外，其余区域的流动可视为理想流体 的无旋运动。
16
旋涡场的几个基本概念：
一、涡线,涡管,旋涡强度 涡线(vortex line)：
向相同时（成锐角）为正,反之为负。
线积分方向相反的速度环量相差一负号，即
ΓAB＝－ΓBA
（5－5)
速度环量的其他表示形式：
AB V ds V cos(V , ds)ds Vxdx Vydy Vzdz
AB
AB
AB
2010-第五章旋涡理论 流体力学

2010-第五章旋涡理论 流体力学


∂ω x ∂ω y ∂ω z + + =0 ∂x ∂y ∂z
∂a x ∂a y ∂a z + + =0 ∂x ∂y ∂z
1 ∂a z ∂a y − vx = ∂z 2 ∂y 1 ∂a x ∂a z v = − y ∂x 2 ∂z 1 ∂a y ∂a x v = z 2 ∂x − ∂y
∫
B
A
ϕ ϕB − ϕ A d=
Γ AB = ∫ V ⋅ ds =
AB
对于有旋场: 由公式
AB
∫ V dx + V dy + V dz
x y
计算 z
2. 若已知速度场，求沿一条闭曲线的速度环量
对于无旋场:
Γc
∂ϕ ∂ϕ ∂ϕ = z dz ∫ c Vx dx + Vy dy + V ∫ c ∂x dx + ∂y dy + ∂z dz dϕ ∫=
n n
1 2
结论： 涡管不能在流体中以尖端形式终止或开始， 否则ｄσ→０时有ω→∞。 涡管存在的形式：要么终止于流体边界或固 体边界，要么自行封闭形成涡环。 不可能 的情况
由该定理得到： 涡管（涡线）本身首尾相接，形成一封闭的涡环或涡圈； 涡管（涡线）两端可以终止于所研究流体的边壁上（固体 壁面或自由面）。
例5.1 已知速度分布，求涡线方程。
ω=const
方法（详见p146）：
例5.2 已知漩涡强度, 求速度环量。
例5.4 已知速度向量，求绕圆心的速度环量。
方法（详见p146）： 由速度环量定义，式（5-1-9），直接积分求得。
旋涡运动基本定理
流体力学漩涡理论(课堂PPT)

流体力学漩涡理论(课堂PPT)


汤姆逊定理: 沿流体质点组成的任一封闭流体 周线的速度环量不随时间而变.
即 d 0
dt .
漩涡理论
22
汤姆逊定理和斯托克斯定理说明：
1) 推论: 2) 流场中原来没有旋涡和速度环量的, 就永远
无旋涡和速度环量。 原来有旋涡和速度环量的，永远有旋涡并保 持环量不变
2）在理想流体中,速度环量和旋涡不生不灭。 因为不存在切向应力，不能传递旋转运动。
第五章：旋涡理论(vortex theory) 1.旋涡场的基本概念（涡线，涡管，旋涡强
度和速度环量） 2.司托克斯定理 3.汤姆逊定理 4.海姆霍兹定理 5.毕奥－沙伐尔定理 6.兰金组合涡
.
1
§５-１ 旋涡运动的基本概念
旋涡场: 存在旋涡运动的流场 有旋运动： ωx,ωy,ωz在流场中不全为零的流动
ABABVxdxVydyVzdzABxdxydryzdzA BdBAVFra bibliotekVsB
对于有旋场:
A B V rd s rV x d x V y d y V zd z
A B
A B
A
d sr
.
漩涡理论
14
2. 若已知速度场，求沿一条闭曲线的速度环量
对于无旋场:
Ñ c cVxdx Vydy Vzdz
流管
涡丝vortex filament 元流
截面积为无限小的涡束 截面积为无限小的流束
称为涡索（涡丝）。
称为元流
.
9
旋涡强度
Ｊ表征流场中旋涡强 弱和分布面积大小
dＪ＝ωndσ
J nd
如果 是涡管的截面
则J为涡管强度
n
r
流量
QdQud
d
阿甘本｜不应该把主体设想为实体，而应该设想为流动中的漩涡。

阿甘本｜不应该把主体设想为实体，而应该设想为流动中的漩涡。

阿甘本｜不应该把主体设想为实体，而应该设想为流动中的漩涡。

文｜阿甘本译｜蓝江第五章漩涡最典型的水的运动是螺旋形的。

当河流中的水流遇到障碍物时，无论是树枝还是桥墩，都会在这一点上产生螺旋运动，如果它被稳定下来，就会呈现出漩涡和连贯性。

如果两股具有不同温度或速度的水流相遇，也会发生同样的情况：即使在这种情况下，我们也会看到漩涡的形成，它们似乎在波浪或水流中保持不动。

但是，在波峰上形成的线圈本身就是一个漩涡，由于重力的作用，它被打成泡沫。

漩涡有它的节奏，这好比行星围绕太阳的运动。

它的内部运动速度高于其外部边缘，就像行星根据其与太阳的距离而旋转得更快或更慢。

在旋转中，漩涡向下延伸，然后以一种脉动向上移动。

此外，如果我们在漩涡中放下一个物体——例如，一小块针状的木头——它将在不断旋转中指向同一个方向，表明一个点，可以说是漩涡的北方。

然而，漩涡不断旋转的中心是一个黑色的太阳，其中有无限的吸力在发挥作用。

根据科学家的说法，这可以通过以下方式来表达：在半径等于零的旋涡点上，压力等于“无限小”。

让我们思考一下，漩涡定义具有何种特殊地位：它是一个从水流中分离出来的形状，而它过去和现在仍然是水流的一部分；一个封闭在自己身上的自主性区域里，遵循着自己的规律。

然而，它与它所在整体有着密切联系，是由与它周围的液体不断物质交换而构成的。

它是一个独立的存在物，但没有任何一滴是单独属于它自己的，它的同一性是绝对非物质性的。

众所周知，本雅明将起源比作一个漩涡：起源（Ursprung）作为一个漩涡处在不断生成的流中，并将所有出现的材料（Entstehung）拼凑成它自己的节奏…… 一方面，作为原初之物希望被恢复和重建，但另一方面，也正是因为如此，作为不完整和未完成的东西。

在每一个原初现象中，都有一个确定的形象，在这个形象中，一个思想将不断面对历史世界，直到它在历史的整体中被揭示出来，得到满足。

因此，起源不是通过对实际发现的检验来发现的，而是与它们的前史和后史有关……因此，起源的范畴并不像科恩（Cohen）所说的那样是一个纯粹的逻辑范畴，而是一个历史范畴。

流体力学漩涡理论ppt课件

速度环量 ：速度矢在积分路径方向的分量沿该
路径的线积分。
定义 AB ABVsds
速度环量是标量，速度方向与
积分AB曲线方向相同时（成锐 角）为正,反之为负。
Γ AB＝－Γ BA
A
V Vs
B
ds
漩涡理论
11
速度环量的其他表示形式：
AB V ds
AB
V cos(V , ds)ds
C L 2 nd
n 0 Γ ｃ＋Γ Ｌ＝０
Γ ｃ=-Γ Ｌ
Ｂˊ Ａˊ ＢＡ
Ｌ
Ｅ
C
Γｃ＝ΓＬ (与积分路径方向一致时)
漩涡理论
21
§5-2 汤姆逊定理
假设：
（1）理想流体；
（2）质量力有势； （3）正压流体（流体密度仅为压力的函数）
汤姆逊定理: 沿流体质点组成的任一封闭流体 周线的速度环量不随时间而变.
第五章：旋涡理论(vortex theory) 1.旋涡场的基本概念（涡线，涡管，旋涡强 度和速度环量） 2.司托克斯定理 3.汤姆逊定理 4.海姆霍兹定理 5.毕奥－沙伐尔定理 6.兰金组合涡
1
§５-１ 旋涡运动的基本概念
旋涡场: 存在旋涡运动的流场 有旋运动： ω x,ω y,ω z在流场中不全为零的流动
流场，非有势力。
漩涡理论
23
§５-３ 海姆霍兹定理
海姆霍兹第一定理
（同一涡管各截面上的旋涡强度都相同）
abdbaea 2 nd
涡a面bdb上aea n0 0
ab ba 0
ab ba
流线微分方程：
取流线上一段微弧长
ds dxi dyj dzk
该处的速度

第五章漩涡理论基础


p

p0

1 2
v2
v02

1 2
v2

1 2
v02

p

1 2

v2
2v02
当 r 0 p pc ,vc 0
故
pc p
p p0
p0

1 2
v02

1 2
v02
p pc
p0 p0
1
2
v02
B vx+(∂vx/∂x)dx
均值。
o
x
注意：v与L垂直时, 0
d
ABCD

1 2
vx


vx

vx x
dx

dx

1 2

vy

vy x
dx



vy

vx x
dx

vy y
dy

dy

1 2

L 2J 2ndA
A
若：周线上各点速度均与周线垂直，则：
L 0
1）、 无限小矩形面积的斯托克斯定理。
在流场中，xoy坐标平面上，取矩形微元周线 ABCD，边长dx，dy，dA=dxdy，如图。 。
A点的速度分量为vx，vy，则B，C，D各点速 度分量如图示（忽略二阶微量），沿微元周
r v
称为涡量
第一节 涡线，涡管，涡束， 旋涡强度
1. 涡线：
在瞬时，涡量场中所作一条空间曲线，该瞬时，
各点的ω均与该线相切，该曲线称为涡线。
涡线为所有质点的转动轴线。注意：涡线是瞬

旋涡理论(vortextheory)

旋涡逐渐变大，其内部的流速 和方向变得更加复杂。
成熟阶段
旋涡达到稳定状态，其形状和 大小不再发生显著变化。
消散阶段
随着时间的推移，旋涡逐渐消 失或与其他旋涡合并。
影响因子
流体性质
流体的密度、粘度、压缩性等物理性质 对旋涡的形成和演化有重要影响。
边界条件
流体的边界形状、粗糙度、弹性等边 界条件对旋涡的形成和演化具有重要
作用
旋涡在湍流中扮演着重要的角色，通过产生速度 梯度和压力梯度，影响流体的流动特性和能量传 递。
研究意义
深入理解旋涡与湍流的关系，有助于揭示湍流的 本质，并为湍流控制和减阻等应用提供理论支持。
漩涡的分离与再附着
定义
漩涡的分离是指流体的旋涡结构在流动过程中发生断裂和分离的现 象；再附着则是指分离后的旋涡重新连接和合并的过程。
对实际应用的推动作用
提高能源利用效率
通过深入理解旋涡现象，优化流体机械设计，提高能源转换效率， 如风力发电机、水力发电等。
环境保护与治理
研究污染物在流体中的扩散和输运机制，利用旋涡理论优化污染控 制和治理方案。
生物医学应用
探索旋涡理论与生物医学的结合点，如血流动力学中的旋涡现象对 心血管疾病的影响等，为疾病诊断和治疗提供新思路。
生态学
在生态学中，旋涡理论用于研究生态系统中的能量流动和物质循环。生态系统中的生物 群落通过食物链和物质循环相互关联，形成复杂的旋涡结构。
流体动力学与生物运动
在研究鱼类、鸟类等生物的运动机制时，旋涡理论用于解释生物如何通过产生旋涡进行 高效的运动和机动。
地球科学
地质学
地质学中，旋涡理论用于研究地 壳板块的运动和相互作用。板块 之间的相互作用形成旋涡结构， 影响地震、火山活动和构造地貌 的形成。

漩涡理论知识点总结

漩涡理论知识点总结一、数学模型在漩涡理论中，最基本的数学模型是涡量方程和涡旋形状方程。

涡量是一个描述流体旋转状态的矢量，它由流速场的旋度给出。

涡量方程描述了在流体中涡量的演变过程，它是流体动力学中的基本方程之一。

涡旋形状方程则描述了在漩涡中流体的轨迹和旋转的形状。

除了涡量方程和涡旋形状方程，漩涡理论还涉及到流体的运动方程和流体的力学性质，如黏性、密度和压力分布等。

这些方程和性质共同构成了漩涡理论的数学模型，通过这些模型可以对流体中的漩涡运动进行准确描述和分析。

二、实验观测漩涡现象在自然界中广泛存在，例如水中的漩涡、大气中的龙卷风、宇宙中的星系旋涡等。

科学家们对这些漩涡现象进行了大量的实验观测，通过这些实验观测积累了丰富的数据和经验，为漩涡理论的研究提供了重要的实验基础。

在实验观测中，科学家们采用了各种现代化的流体力学实验设备和技术手段，如风洞实验、水池实验、激光测速仪等。

通过这些实验手段，可以对漩涡的形成、演变和消散过程进行详细观测和记录，从而揭示了漩涡运动的一些重要规律和特性。

三、应用漩涡理论除了在基础理论研究中有重要意义外，还在工程技术、环境科学、气象预报等领域有着广泛的应用。

例如，在航空航天领域，漩涡理论被用于设计和优化飞行器的气动外形，以降低飞行器的阻力和提高飞行性能。

在水利工程中，漩涡理论可以用来预测水流的流速和方向，为水利工程的设计和施工提供重要的参考依据。

在海洋工程中，漩涡理论可以帮助科学家们理解海流的形成和演变规律，为海洋资源开发和环境保护提供支持。

总之，漩涡理论是流体动力学中的重要理论之一，它是对流体中漩涡运动规律的系统总结和理论探讨。

通过数学模型、实验观测和应用研究，科学家们不断深化了对漩涡理论的理解和认识，为人类对自然界中漩涡现象的研究和利用提供了重要的理论和技术支持。

希望在未来的研究中，漩涡理论能够继续发展和完善，为人类对自然界的探索和认识作出更大的贡献。

第五章 旋涡


该定理说明：涡管或涡束既不能在流体中开始，也不能 在流体中终止，它必须呈现为闭合环形，或者从流体边 界(容器壁面或自由面)上开始或终止，如图5-3所示。例 如抽烟者喷的烟圈成圆形烟环，自然界中的龙卷风开始 和终止于水面和云层等边界面。
图5-3
第三节 流体运动的一些基本概念

迹线与流线
迹线是流场中其一质点运动的轨迹。 例如在流动的水面上撤一片木屑，木屑随水流漂流的途径就是某一水点的 运动轨迹，也就是迹线。流场中所有的流体质点都有自己的迹线，迹线是流 体运动的一种几何表示，可以用它来直观形象地分析流体的运动，清楚地看 出质点的运动情况。迹线的研究是属于拉格朗日法的内容，迹线农示同一流 体质点在个同时刻所形成的曲线。 流线是某一瞬时在流场中所作的一条曲线，在这条曲线上的各流体质点的速 度方向都与该曲线相切，因此流线是同一时刻不问流体质点所组成的曲线。 流线可以形象地给出流场的流动状态。通过流 线，可以清楚地看出某时刻流场中各点的速度 方向，由流线的密集程度，也可以判定出速度 的大小。流线的引入是欧拉法的研究特点。例 如在流动水面上同时撤一大片木屑，这时可看 到这些木屑将连成若干条曲线，每一条曲线表 示在同一瞬时各水点的流动方向线，就是流线。
2 n dA
A
第三节 汤姆生定理和亥姆霍兹定理 一、汤姆生定理 汤姆孙(W．Thomson)定理：正压性的理想流体在有势的质量力作用下沿任 何由流体质点所组成的封闭周线的速度环量不随时间而变化。
根据斯托克斯定理和汤姆孙定理可知：旋涡强度直接由速度环 量所度量。在理想流体中始终由某一些流体质点所组成的任意 封闭曲线的速度环量既然保持为常数，与时间无关，也就是它 的旋涡强度保持为常数，且与时间无关。这样流体在运动过程 中本来是无旋流动就不可能变为有旋流动；或者相反，本来具 有旋涡就不能消失。当然这是因为将流体看作为理想的，不考 虑粘性影响的缘故。事实上在真实流体中旋涡将会产生也会消 失。但是在较短时间内，粘性力影响较小时，可以近似地认为 满足汤姆孙定理的条件，而用它来阐明某些现象。

旋涡理论ppt课件

单连通区域内的无旋运动，流体 中的旋度处处为零，则沿任意封 闭周线的速度环量为零，即：
C 2nd 2 0d 0


反之，若沿任意封闭周线的速度环量等于零，可得处处为 零的结论。
但沿某闭周线的速度环量为零，并不一定无旋（可能包围强
度相同转向相反的旋涡）。
推论二
对于包含一个翼截面在内的双连通区域，如果流动是无旋的，
旋涡运动理论广泛地应用于工程实际: 机 翼、螺旋桨理论等。旋涡与船体的阻力、振动、 噪声等问题密切相关。
旋涡的产生： 与压力差、质量力和粘性力等
因素有关。
流体流过固体壁面时，除壁面附近粘性影响严 重的一薄层外，其余区域的流动可视为理想流体 的无旋运动。
4
旋涡运动基本概念
流场
涡场
流速v
涡量 Ω
流量Q
Thomson定理和Lagrange 定理适用条件为： 1. 理想流体
2. 正压流体 ( p)
3. 在有势质量力作用下
旋涡起因： (1) 粘性：均匀流体经过物体边界层时运动变为有旋； (2) 非正压流场：大气和海洋中的密度分层形成旋涡； (3) 非有势力场：地球哥氏力使气流生成旋涡（旋风）； (4) 流场的间断（非连续）：曲面激波后形成有旋流动。 19
亥姆霍兹（Helmholtz）定理 （1）亥姆霍兹第一定理：
——涡管强度空间守恒
在同一瞬间涡管各截面上 的旋涡强度都相同
由斯托克斯定理 abdbaea 2 nd
因为内ωｎ＝０所以 0
由斯托克斯定理上式写成:
nd nd
1
2
20
结论： 涡管不能在流体中以尖端形式终止或开始， 否则ｄσ→０时有ω→∞。
15
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

11．若流场不是静止的，具有均匀速度 V，毕奥——沙伐尔诱导速度场的计算公式所计算出
的速度是否包含有均匀速度 V？
12．圆柱形涡，在 r< R 和 r>R 两个流场中，压力和速度分布如何？
13.已知平面流动的速度分布为：
u = x2 − y2 + x
v = −2xy − y
证明沿曲线 R2 = x2 + y2 的速度环量和流量均为零。
6.B-S 定理只适用于（
）
A）理想流体
B）不可压缩流体
C）粘性流体
D）理想流体或粘性流体
7．为什么涡线不能在流场中终止，只能终止在固体边界，或者流体边界，或者首尾相接形
成涡环。
8.对于无旋流场，存在速度势，是否存在环量Γ？为什么？
9．流体周线与流线有何差别？
10．涡线所诱导的速度场都是无旋场吗？为什么？
3.海姆霍兹定理
定理一：同一瞬时，涡管各截面上的涡管强度不变，
即 ∫∫ωndσ = ∫∫ ωndσ = const
σ1
σ2
定理二：前提为理想、正压流体，质量力有势，涡管永远由相同的流体质点所组成，又称
涡管保持定理。
定理三：前提为理想、正压流体，质量力有势，任何涡管的旋涡强度不随时间变化，又称
涡管强度保持定理。
推论二：无旋场内有一物体，则包含该物体在内的任意封闭曲线的环量不变。
速度环量Γ的计算： 归纳如下：
（1）沿任意闭曲线的速度环量
对于无旋场：
∫ ∫ ∫ Γ =
B
A Vx dx + Vy dy + Vz dy =
B ∂ϕ dx + ∂ϕ dy + ∂ϕ dy =
A ∂x
∂y
∂z
B dϕ = 0
A
对于有旋场：
cy y2 + z2
ωy
=
1 (∂vx 2 ∂z
− ∂vz ) = ∂x
cz y2 + z2
ωx
=
1 (∂vz 2 ∂y
−
∂vy ) ∂z
=0
JK 所以：ω =
c
KK (z j − yk)
y2 + z2
2）由涡线微分方程 dx = dy = dz ， ωx ωy ωz
有 积分得
dy = − dz zy y2 + z2 = c1
R2
+
⎤ 1⎥
⎪⎫ ⎬
R42 + R22 ⎥⎦⎪⎭
四、思考题及练习题
1．一物体在静止不可压缩理想流体中作等速直线运动，则流场为（ ）。
A）定常不可压缩无旋流场
B）静止，不可压缩理想流场
C）不可压缩有旋流场
D）不可压缩非定常流场
JK
v∫ ∫∫ 2．斯托克斯定理 Γ = c vsds = 2 wndσ ，若 Γ =0，而ω 不一定为零，这是因为（ ）。 σ
R3
R2
Γ
Γ
R1
Γ
x = c2
5．试求图 5-2 所示的马蹄涡对流场中任意一点 处的诱导速度。 解：设流场中任意一点 A，分别距三条涡线的垂
α4
α5
α6
α2 α3
α1
直距离为 R1, R2 , R3 ，由直线涡的公式
图 5-2
v
=
Γ 2π h
(cos a1
−
cos a2 )
应为三条涡线对 A 点的诱导速度之和，即：
R4 r2
− ρ gz
(r > R)
p0
+
ρω 2 2
r2
−
ρω2 R2
−
ρ gz
(r < R)
二．重点，难点
重点：
1. 旋涡场的几个概念，如涡线，涡管，涡管强度，速度环量，圆柱形涡的速度分布，
压力分布规律。
2.斯托克斯定理，汤姆孙定理，海姆霍兹三定理的前提，结论。
3. 斯托可斯定理的应用，速度环量的计算，旋涡强度的计算。
4．毕奥——沙伐尔定理的应用。
难点：毕奥——沙伐尔定理的应用。
三、例题
1．已知闭曲线为半径 R=0.5m 的圆，其上各点上流体质点的速度 vθ = 2 m s ，试求沿此闭曲
线的速度环量。
v∫ ∫ 解： Γ =
R=0.5 vθ dl =
2π 0
vθ
Rdθ
=
6.28 m2
s
JK
2．如图 5-1 的平面极坐标内，已知 r > a 时ω = 0 ，当 a ≤ r 时，ωx = ωy = 0 ，ωz = ω（顺
A）σ 不是 c 所围的区域
B）流体是有粘性的
C）在σ 内 ωn 的求和为零，而σ 内的流场可能有旋 D）σ 为复连通域 3．一封闭曲线 c，有 n 个强度为Γ的涡线穿过 c 所围的区域σ ，且每根涡线都与 c 所围的区
域正交，则绕曲线 c 的环量为（ ）。
A） Γ
B）n Γ
C） Γ σ
4.海姆霍兹第一定理和第三定理表明（
p0
=
1 2
ρ vθ 2
−
ρ vR 2
p − p0 = −ρvR2
（ r < R ） 有旋 （r > R ） 无旋
（r<R） （r=0）
其中 vR 为 r=R 时的速度
p
=
p0
−
1 2
ρ vθ 2
兰金涡：铅直圆柱形涡，顶部为自由液面。
压力分布：
（r > R ）
⎧ ⎪⎪
p
=
⎨
⎪ ⎪⎩
p
=
p0
−
ρω 2 2
4. 毕奥——沙伐尔定理
不可压缩流场中任意一条涡线，旋涡强度为Γ，其诱导速度场的计算公式：
∫ v = Γ sinθ ds
4π s r 2
式中：r 为空间点 p 到涡线的向径， θ 为 r 与 ds 的夹角，ds 为涡线的微分弧长。
对于任意一条直线涡： v
=
Γ 4π R
(cosθ1
−
cosθ2 )
对于无穷长直线涡： v = Γ 2π R
vA
=
Γ 4π R1
(cosα1
− cosα2 )
+
Γ 4π R2
(cosα3
−
cosα4 )
+
Γ 4π R3
(cosα5
−
cosα6 )
其中
α1
=0， α 2
=π
−
arctg
R1 R2
cosα2 =
− R2 R12 + R22
α3
=
arctg
R2 R1
cosα3 =
R2 R12 + R22
α4
=
π
14.不可压缩流体作平面均匀流动，
y D(0,1)
(1)流动均匀，大小为 U,计算沿路径 ABCD 的速度环量。 U
(2)若速度分布不是均匀的，而是
u = −x − y
v= y
A(0,0)
C(1,1)
x B(1,0)
计算沿路径 ABCD 的速度环量。
图 5-3
15.不可压缩平面涡量场，在半径为 R 的圆形域内，涡通量为 J,已知在半径为 r 处的流体速
r ≤ a 时，ωz = ω ，
r > a 时 ωz = 0 ，式中 a，ω为常数，求速度分布。
∫ 解：（1）当 r
≤
a 时 vr
=
vz
=
0 ，由 Γ
=
2
σ
wndσ
，有 vθ
⋅ 2π r1
=
2ω
⋅
π
r
2 1
所以 vθ = rω
（2）当 r>a 时， vz = vr = 0 同理 vθ ⋅ 2π r1 = 2ω ⋅ π a2
速度场与旋涡场的对比：
JG
速度场
V
GG
流线
V // dl
流线微分方程
dx = dy = dz vx vy vz
流管：流管的母线是流线
G JG 体积流量： dQ = V ⋅ dσ = Vn ⋅ dσ
二维不可压缩流动： QAB =ψ B −ψ A G
不可压缩流体连续性方程： ∇ ⋅V = 0
旋涡场 涡线
第五章：旋涡理论
一．内容小结：
旋涡运动是流体流动中的常见现象，将流场分为有旋流场和无旋流场有助于解决流体力 学问题。本章仅从运动学的角度讨论旋涡运动。 1．旋涡运动的几个基本概念
涡线：同流线定义相似，即同一瞬时涡线上每一流体质点的旋转角速度矢量与涡线相切。 涡线微分方程：
dx = dy = dz ωx ωy ωz
v∫ ∫∫ 可由斯托克斯公式 c vs ds = 2 ωndσ 计算 σ
（2）沿一条开曲线 AB 的速度环量 对于无旋场：
∫ ∫ ∫ Γ =
B
A Vx dx + Vy dy + Vz dy =
B ∂ϕ dx + ∂ϕ dy + ∂ϕ dy =
A ∂x
∂y
∂z
B dϕ
A
=
ϕB
− ϕA
对于有旋场：
B
∫ 直接由 Γ = A Vxdx + Vy dy + Vz dy 计算
v∫ ∫∫ 斯托克斯定理： c vs ds = 2 ωndσ σ
适用条件是单连通域（即闭曲线 c 内没有空洞，物体等），对于复连通域，挖去空洞，
物体等仍可变为单连通域来处理。
∫∫ 推论一：单连通域内， ωG 处处为零。则Γ=0。即 Γ = 2 ωndσ = 0 σ
但沿着某一闭曲线的环量Γ=0，而ωG 不一定为零。