当前位置：文档之家 › 【高考调研】高考数学 1-2 命题及其关系、充要条件精品复习课件

【高考调研】高考数学 1-2 命题及其关系、充要条件精品复习课件

  • 格式：ppt
  • 大小：786.50 KB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

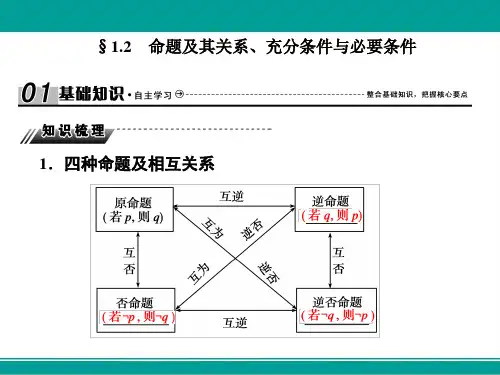
高三高考数学复习课件1-2命题及其关系充分条件与必要条件

高三高考数学复习课件1-2命题及其关系充分条件与必要条件


跟踪训练1 (1)命题“若x，y都是偶数，则x＋y也是偶 数”的逆否命题是( )
A．若x＋y是偶数，则x与y不都是偶数 B．若x＋y是偶数，则x与y都不是偶数 C．若x＋y不是偶数，则x与y不都是偶数 D．若x＋y不是偶数，则x与y都不是偶数
(2)设原命题：若a＋b≥2，则a，b中至少有一个不小于 1，则原命题与其逆命题的真假情况是( )
【答案】 A
题型一 命题及其关系 【例1】 (1)命题：“若x2<1，则－1<x<1”的逆否命题 是( ) A．若x2≥1，则x≥1或x≤－1 B．若－1<x<1，则x2<1 C．若x>1或x<－1，则x2>1 D．若x≥1或x≤－1，则x2≥1
(2)(2018·石家庄模拟)命题“若一个数是负数，则它的 平方是正数”的逆命题是( )
1－m≤1＋m， 则1－m≥－2， ∴0≤m≤3.
1＋m≤10，
∴当 0≤m≤3 时，x∈P 是 x∈S 的必要条件，即所求 m 的取
值范围是[0，3]．
【思维升华】 充分条件、必要条件的应用，一般表现 在参数问题的求解上．解题时需注意：
(1)把充分条件、必要条件或充要条件转化为集合之间的 关系，然后根据集合之间的关系列出关于参数的不等式(或 不等式组)求解．
p是q的_充__分__不__必__要___条件
p⇒q且q⇒ p
p是q的__必__要__不__充__分___条件
p q且q⇒p
p是q的_充__要__条件
p⇔q
p是q的_既__不__充__分__也__不__必__要___条件 p q且q p
【知识拓展】 从集合角度理解充分条件与必要条件
若p以集合A的形式出现，q以集合B的形式出现，即A＝ {x|p(x)}，B＝{x|q(x)}，则关于充分条件、必要条件又可以 叙述为
最新高三一轮：1-2《命题及其关系、充分条件与必要条件》ppt课件

最新高三一轮：1-2《命题及其关系、充分条件与必要条件》ppt课件

若綈 p, 则綈 q
若 q，则 p
若綈 q, 则綈 p
(2)四种命题的真假关系
两个命题互为逆否命题，它们有□7 相__同__的真假性； 两个命题互为逆命题或互为否命题，它们的真假性□8 __无__关______。
3．充分条件与必要条件
(1)如果 p⇒q，那么 p 是 q 的□9 __充__分__条__件____，q 是 p 的□10 _必__要__条__件___。 (2)如果 p⇒q，q⇒p，那么 p 是 q 的□11 _充__要__条__件___。
D．若 tanα≠1，则 α＝π4
解析：以否定的结论作条件、否定的条件作结论得出的命题为逆否命题，即“若 α＝π4，则 tanα＝1”的逆否命题是“若 tanα≠1，则 α≠π4”，故选 C。
答案：C
3．设集合 A，B，则“A⊆B”是“A∩B＝A”成立的( )
A．充分不必要条件
B．必要不充分条件
C．充要条件
C．若 x＝y，则 x＝ y D．若 x＜y，则 x2＜y2
解析：由1x＝1y得 x＝y，A 正确，易知 B、C、D 错误， 故选 A。 答案：A
2．命题“若 α＝π4，则 tanα＝1”的逆否命题是( )
A．若 α≠π4，则 tanα≠1
B．若 α＝π4，则 tanα≠1
C．若 tanα≠1，则 α≠π4
•
ห้องสมุดไป่ตู้
10、低头要有勇气，抬头要有低气。2 021/5/ 112021 /5/1120 21/5/1 15/11/2 021 6:50:39 AM
•
11、人总是珍惜为得到。2021/5/1120 21/5/11 2021/5 /11Ma y-2111-May-21
•
【高考调研】高考数学 1-2 命题及其关系、充要条件精品复习课件

【高考调研】高考数学 1-2 命题及其关系、充要条件精品复习课件

2
高考调研 ·新课标高考总复 习
3 (4)p：ΔABC 中，∠A≠60°，q：sinA≠ . 2 → → → (5)设向量AB＝a，BC＝b，CA＝c，p：A、B、C 三点构 成三角形；q：a＋b＋c＝0 【解析】 (1)必要不充分条件．(2)充分不必要条件．
(3)p：x≤－1 或 x≥3，∴p⇒q，但 q⇒ / p，故 p 是 q 的充分不必要条件． (4)p⇒ / q，q⇒p，∴p 是 q 的必要不充分条件 (5)p⇒q，但 q⇒ / p，∴p 是 q 的充分不必要条件
(2)原命题与它的逆否命题等价； 逆命题与它的否命题等价．
高考调研 ·新课标高考总复 习
3．充分条件与必要条件 ( 1) 若 p⇒ q 且 q ⇒ / p，则 p 是 q 的充分非必要条件； ( 2) 若 q⇒ p 且 p ⇒ / q，则 p 是 q 的必要非充分条件； ( 3) 若 p⇒ q 且 q ⇒ p，则 p 是 q 的充要条件； ( 4) 若p ⇒ / q且q ⇒ / p，则 p 是 q 的非充分非必要条件．
以a>0是|a|>0的充分不必要条件，故选A.
高考调研 ·新课标高考总复 习
授人以渔
题型一 四种命题及其真假的判断
例1 分别写出下列命题的逆命题、否命题、逆否命题，并判断它们的 真假． (1)面积相等的两个三角形是全等三角形． (2)若q<1，则方程x2＋2x＋q＝0有实根． (3)若x2＋y2＝0，则实数x，y全为零． 【解析】 (1)逆命题：全等三角形的面积相等．真命题． 否命题：面积不相等的两个三角形不是全等三角形．真命题．
高考调研 ·新课标高考总复 习
探究1 ①此类题应先把原命题改写成“若p，则q“的形式，然后再写
出其他命题． 对于含有大前提的命题，在改写命题形式时，大前提不要动．
高考数学一轮总复习 1.2命题及其关系、充分条件与必要条件课件

高考数学一轮总复习 1.2命题及其关系、充分条件与必要条件课件


②命题“若a＝0，则ab＝0”的否命题是“若a≠0，则
ab≠0”；
③命题“若x，y都是偶数，则x＋y也是偶数”的逆命题为真
命题；
④命题“若a∈M，则b∉M”与命题“若b∈M，则a∉M”等
价．
精选ppt
26
解析
(1)命题“若α＝
π 4
，则tanα＝1”的逆否命题是“若
tanα≠1，则α≠4π”．
精选ppt
答案 (1)A (2)A
精选ppt
31
【规律方法】 充要条件的判断，重在“从定义出发”，利 用命题“若p，则q”及其逆命题的真假进行区分，在具体解题 中，要注意分清“谁是条件”“谁是结论”．有时还可以通过其 逆否命题的真假加以区分．
精选ppt
32
变式思考 2 (1)设a，b为向量，则“|a·b|＝|a||b|”是“a∥ b”的( )
答案 (1)C (2)②④
精选ppt
28
考点二 充分条件与必要条件的判断
【例2】 (1)给定两个命题p，q.若綈p是q的必要而不充分条
件，则p是綈q的( ) A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件
精选ppt
29
(2)“φ＝π”是“曲线y＝sin(2x＋φ)过坐标原点的”( ) A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件
27
(2)对于①，若log2a>0＝log21，则a>1，所以函数f(x)＝logax 在其定义域内是增函数，故①不正确；对于②，依据一个命题的 否命题的定义可知，该说法正确；对于③，原命题的逆命题是 “若x＋y是偶数，则x、y都是偶数”，是假命题，如1＋3＝4是偶 数，但3和1均为奇数，故③不正确；对于④，不难看出，命题 “若a∈M，则b∉M”与命题“若b∈M，则a∉M”互为逆否命 题，因此二者等价，所以④正确．综上可知正确的说法有②④.
高考数学总复习 1-2 命题及其关系、充分条件与必要条件课件 苏教版

高考数学总复习 1-2 命题及其关系、充分条件与必要条件课件 苏教版


【点评】
由于互为逆否命题的两个命题是等价命题，它们同
真同假，所以一个命题的逆命题和它的否命题同真同假；一个命题 与它的逆否命题同真同假．当一个命题的真假不易判断时，可以通 过判断其逆否命题的真假来判断．
1． (2013· 扬州联考)以下关于命题的说法正确的有________(填写 所有正确命题的序号)． ①“若 log2a>0，则函数 f(x)＝logax(a>0，a≠1)在其定义域内是 减函数”是真命题； ②命题“若 a＝0， 则 ab＝0”的否命题是“若 a≠0， 则 ab≠0”； ③命题“若 x， y 都是偶数， 则 x＋y 也是偶数”的逆命题为真命 题； ④命题“若 a∈M， 则 b∉M”与命题“若 b∈M， 则 a∉M”等价．
考向二
充要条件的判断
(2013· 宿迁期末)指出下列命题中，p 是 q 的什么条件(在 “充分不必要条件”、“必要不充分条件”、“充要条件”、“既 不充分也不必要条件”中选出一种作答)． (1)在△ABC 中，p：∠A＝∠B，q：sin A＝sin B； (2)对于实数 x、y，p：x＋y≠8，q：x≠2 或 y≠6； (3)非空集合 A、B 中，p：x∈A∪B，q：x∈B； (4)已知 x、y∈R，p：(x－1)2＋(y－2)2＝0，q：(x－1)(y－2)＝0.
【基础自测】 1．若伸开 p 的否命题为 r，命题 r 的逆命题为 s，则 s 是 p 的逆 命题 t 的________命题． 答案：否 2．已知 a，b 都是实数，那么“a2>b2”是“a>b”的________条件． 答案：既不充分也不必要 3．(2011· 高考山东卷)已知 a，b，c∈R，命题“若 a＋b＋c＝3， 则 a2＋b2＋c2≥3”的否命题是________． 答案：已知 a，b，c∈R，若 a＋b＋c≠3，则 a2＋b2＋c2<3
【优化探究】高考数学一轮复习 1-2 命题及其关系、充分条件与必要条件课件 文

【优化探究】高考数学一轮复习 1-2 命题及其关系、充分条件与必要条件课件 文


二、充分条件与必要条件 3．(2014年高考广东卷)在△ABC中，角A，B，C所对应的边分别
为a，b，c，则“a≤b”是“sin A≤sin B”的(
A．充分必要条件 B．充分非必要条件
)
C．必要非充分条件
D．非充分非必要条件
a b 解析：由正弦定理 ＝ ＝2R(R 为三角形外接圆半径)得，a＝ sin A sin B 2Rsin A，b＝2Rsin B，故 a≤b⇔2Rsin A≤2Rsin B⇔sin A≤sin B，故选 A.
么(q)．
2．尝试用条件推结论，再尝试用结论推条件，推理方法可以用直 接证明法或间接证明法．
3．确定条件是结论的什么条件，抓住“以小推大”的技巧，即小
范围推得大范围． 4．判断的结论需分四种情况：充分不必要条件、必要不充分条件、
充要条件、既不充分也不必要条件．
一、四种命题及其关系 1．判断下列结论的正误．(正确的打“√”，错误的打“×”) (1)语句x2－3x＋2＝0是命题( ) ) (2)一个命题的逆命题与否命题，它们的真假没有关系( 立”( ) )
(3)命题“如果p不成立，则q不成立”等价于“如果q成立，则p成
(4)“p是q的充分不必要条件”与“p的充分不必要条件是q”表达
的意义相同(
解析：(1)变量 x 没有赋值，无法判断语句的真假，故不是命题． (2)一个命题的逆命题与否命题互为逆否命题，因此它们有相同的真 假性． (3)一个命题与其逆否命题同真假． (4)p 是 q 的充分不必要条件是指 p⇒q 且 q 件是 q 是指 q⇒p 且 p p；p 的充分不必要条
三、四种命题的真假关系
1．两个命题互为逆否命题，它们有 相同 的真假性． 2．两个命题互为逆命题或互为否命题，它们的真假性 没有 关
高考数学一轮复习 1.2命题及其关系、充分条件与必要条件课件 文

高考数学一轮复习 1.2命题及其关系、充分条件与必要条件课件 文


精品
22
解析：命题“若 a2＋b2＝0，a，b∈R，则 a＝b＝0”的逆否 命题是“若 a≠0 或 b≠0，a，b∈R，则 a2＋b2≠0”．
答案：A
精品
23
考点二 充分条件与必要条件的判断 1.利用定义判断 (1)若 p⇒q，则 p 是 q 的充分条件； (2)若 q⇒p，则 p 是 q 的必要条件； (3)若 p⇒q 且 q⇒p，则 p 是 q 的充要条件；
第
一
集合、常用逻辑用语
章
精品
1
第二节
命题及其关系、充分条件与必要条件
精品
2
高考导航ห้องสมุดไป่ตู้
精品
3
基础
知识回顾
精品
4
1．命题的概念 在数学中用语言、符号或式子表达的，可以 判断真假 的语 句叫做命题．其中 判断为真 的语句叫真命题，判断为假的语句 叫假命题． 2．四种命题及其关系 (1)四种命题
精品
5
精品
8
3．充分条件与必要条件 (1)如果p⇒q，则p是q的 充分条件 ，q是p的 必要条件 ； (2)如果p⇒q，q⇒p，则p是q的 充要条件．
精品
9
在判断充分条件与必要条件时，一定要注意弄清问题的设问 方式，“A 是 B 的充分不必要条件”与“A 的充分不必要条件是 B”两种说法的含义是不同的．
2．对于命题真假的判定，关键是分清命题的条件与结论， 只有将条件与结论分清，再结合所涉及的知识才能正确地判断命 题的真假．
精品
17
原命题与其逆否命题同真同假．
精品
18
(2014·陕西卷)原命题为“若an＋2an＋1<an，n∈N＋，则{an}为 递减数列”，关于其逆命题，否命题，逆否命题真假性的判断依 次如下，正确的是( )
高考数学一轮复习 1-2命题及充要条件课件 文

高考数学一轮复习 1-2命题及充要条件课件 文


a≤1，
当只有一个负实根时，1a＜0
⇒a＜0；
基础诊断
考点突破
课堂总结
a≤1， 当有两个负实根时，－2a＜0，⇒0＜a≤1.
1a＞0
综上述，a≤1.
• 答案 (1)必要不充分 (2)a≤1
基础诊断
考点突破
课堂总结
•规律方法 判断p是q的什么条件，需要从两方 面分析：一是由条件p能否推得条件q；二是由条 件q能否推得条件p.对于带有否定性的命题或比 较难判断的命题，除借助集合思想把抽象、复杂 问题形象化、直观化外，还可利用原命题和逆否 命题、逆命题和否命题的等价性，转化为判断它 的等价命题．
解析 a＝3 时，A＝{1,3}，显然 A⊆B.
但 A⊆B 时，a＝2 或 3.所以“a＝3”是“A⊆B”的充分不必
要条件．
答案 充分不必要
基础诊断
考点突破
课堂总结
• 4．(2014·浙江卷改编)设四边形ABCD的两条 对角线为AC，BD，则“四边形ABCD为菱形” 是“AC⊥BD”的________条件(填“充分不必 要”、“必要不充分”、“充要”、“既不充 分也不必要”)．
∈B”的充分条件或“x∈B”是“x∈A”的必要条件；若 A＝
B，则“x∈A”是“x∈B”的充要条件．
• [易错防范]
• 对于命题正误的判断是高考的热点之一，
理应引起大家的关注，命题正误的判断可涉及
各章节的内容，覆盖面宽，也是学生的易失分
点．命题正误的判断的原则是正确的命题要有
依据或者给以论证；不一定正确的命题要举出
第2讲 命题及充要条
件 • 考试要求 1.命题的概念，命题的四种形式
及相互关系，A级要求；2.充分条件、必要条 件、充要条件的含义，B级要求．
高考数学(理)课件：1-2命题及其关系、充要条件

高考数学(理)课件：1-2命题及其关系、充要条件


②再证必要性：∵对任意x∈[0,1]，|f(x)|≤1， ∴f(1)≥－1，即a≥b－1； ∵对任意x∈[0,1]，|f(x)|≤1，而b>1，
∴f
1 ≤1，即a≤2 b，必要性得证． b
由①②可知，当b>1时，对任意x∈[0,1]，|f(x)|≤1成立的充 要条件是b－1≤a≤2 b.
规律方法 (1)涉及参数问题，直接解决较为困难，先用等价 转化思想，将复杂、生疏的问题化归为简单、熟悉的问题来 解决． (2)①p的充分不必要条件为q，等价于p⇐q，q 要不充分条件为q，等价于p⇒q，q p. p；②p的必
【训练1】 (2013·吉林白山二模)命 题 “若 a2 ＋ b2 ＝ 0 ， 则 a ＝ 0 且 b ＝ 0”的逆否命题是________． 答案 若 a≠0 或 b≠0 ，则 a2 ＋ 2 b ≠0
考点二 充分条件、必要条件的判断 【例 2】 (1)(2013· 福建卷改编 ) 设点 P(x ， y) ， 则 “ x ＝ 2 且 y ＝ － 1” 是 “点 P 在直线 l ： x ＋ y － 1 ＝ 0 上”的 ________条件． (2)(2013· 济南模拟 ) 如果 a ＝ (1 ， k)， b＝ (k,4)，那么“ a∥b”是“ k ＝ －2”的________条件． 解析 (1)当x＝2且 y＝－ 1时，满 足方程x＋y－1＝0，

规律方法 判断p是q的什么条件， 需要从两方面分析：一是由条件p 能否推得条件q；二是由条件q能否 推得条件p.对于带有否定性的命题 或比较难判断的命题，除借助集合 思想把抽象、复杂问题形象化、直 观化外，还可利用原命题和逆否命 题、逆命题和否命题的等价性，转 化为判断它的等价命题．
1 【训练2】 已知条件p：x≤1，条件q：x ＜1，则綈p是q的 ________条件．
高考数学北师大版二轮复习课件1-2 命题及其关系充分条件与必要条件

高考数学北师大版二轮复习课件1-2 命题及其关系充分条件与必要条件


(3)可转化为集合间的包含关系来判断．
【自主试解】
(1)若∠A＝∠B，则 sin A＝sin B，即 p⇒q.
又若 sin A＝sin B，则 2Rsin A＝2Rsin B，即 a＝b. ∴∠A＝∠B，即 q⇒p.所以 p 是 q 的充要条件． f－x (2)∵ ＝1， fx ∴f(－x)＝f(x)， ∴y＝f(x)是偶函数，∴p⇒q. 取 f(x)＝x2 为 R 上的偶函数， f－x 但 在 x＝0 时没有意义，∴q⇒/p. fx ∴p 是 q 的充分不必要条件．
并写出否命题、逆否命题，然后证明所得结论，判定真假． 【自主试解】 (1)否命题：已知函数 f(x)在(－∞，＋∞)上是增 加的，若 a＋b<0，则 f(a)＋f(b)<f(－a)＋f(－b)． 否命题为真命题，证明如下： ∵f(x)在(－∞，＋∞)上是增加的，
若 a＋b<0，则 a<－b，b<－a， ∴f(a)<f(－b)，f(b)<f(－a)． ∴f(a)＋f(b)<f(－a)＋f(－b)， 故否命题为真命题． (2)逆否命题：已知函数 f(x)在(－∞，＋∞)上是增加的，若 f(a) ＋f(b)<f(－a)＋f(－b)，则 a＋b<0. 该逆否命题为真命题，证明如下：
) B．若 x2＝1，则 x＝1 D．若 x＜y，则 x2＜y2
1 1 解析：由 ＝ 可得 x＝y；由 x2＝1 可得 x＝± 1；由 x＝y，则 x， x y y不一定有意义；而 x＜y 不一定得到 x2＜y2. 答案：A
二、四种命题及其关系 1.
2．四种命题的真假关系 (1)两个命题互为逆否命题，它们有 相同 的真假性； (2)两个命题互为逆命题或互为否命题，它们的真假性没有关系 ．
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高考调研 ·新课标高考总复 习
探究1 ①此类题应先把原命题改写成“若p，则q“的形式，然后再写 出其他命题． 对于含有大前提的命题，在改写命题形式时，大前提不要动． ②若说明命题为真，必须证明．若说明为假，只需举出一个反例即可． ③否命题是难点，注意量词和逻辑联结词．
高考调研 ·新课标高考总复 习
A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件
)
答案 A
解析 |x－2|<4得－2<x<6 5．(2010· 陕西卷)“a>0”是“|a|>0”的( )
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件 答案 A
解析 因为|a|>0⇔a>0或a<0，所以a>0⇒|a|>0，但|a|>0 a>0，所
逆否命题：两个不全等的三角形的面积不相等．假命题．
高考调研 ·新课标高考总复 习 (2)逆命题：若方程x2＋2x＋q＝0有实根，则q<1.假命题． 否命题：若q≥1，则方程x2＋2x＋q＝0 逆否命题：若方程x2＋2x＋q＝0无实根，则有q≥1.真命题． (3)逆命题：若实数x，y全为零，则x2＋y2＝0.真命题． 否命题：若x2＋y2≠0，则实数x，y不全为零．真命题． 逆否命题：若实数x，y不全为零，则x2＋y2≠0.真命题．
(2)原命题与它的逆否命题等价； 逆命题与它的否命题等价．
高考调研 ·新课标高考总复 习
3．充分条件与必要条件 ( 1) 若 p⇒ q 且 q ⇒ / p，则 p 是 q 的充分非必要条件； ( 2) 若 q⇒ p 且 p ⇒ / q，则 p 是 q 的必要非充分条件； ( 3) 若 p⇒ q 且 q ⇒ p，则 p 是 q 的充要条件； ( 4) 若p ⇒ / q且q ⇒ / p，则 p 是 q 的非充分非必要条件．
(2)逆命题：若方程ax2＋2x＋1＝0至少有一个负数根，则a<0.
高考调研 ·新课标高考总复 习
否命题：若q≥1，则方程x2＋2x＋q＝0无实根．假命题． 逆否命题：若方程x2＋2x＋q＝0无实根，则有q≥1.真命题． (3)逆命题：若实数x，y全为零，则x2＋y2＝0.真命题． 否命题：若x2＋y2≠0，则实数x，y不全为零．真命题． 逆否命题：若实数x，y不全为零，则x2＋y2≠0.真命题．
并判断它们的真假． (1)若a>b且c>d，则a＋c>b＋d (2)(08· 安徽卷改编)若a<0，则方程ax2＋2x＋1＝0至少有一个负 数根． 【解析】 (1)逆命题：若a＋c>b＋d，则a>b且c>d(假命题) 否命题：若a≤b或c≤d，则a＋c≤b＋d(假命题)
逆否命题：若a＋c≤b＋d，则a≤b或c≤d(真命题)
高考调研 ·新课标高考总复 习
3．(2011· 山东师大附中)设原命题“若p，则q”假，而逆命题真，则p是q的 ( ) B．必要不充分条件
A．充分不必要条件 C．充要条件 答案 B
D．既不充分也不必要条件
⇒ /
解析 原命题假，则 p q，而逆命题为真，则q⇒p.
高考调研 ·新课标高考总复 习
4．0＜x＜5是不等式|x－2|＜4成立的(
思考题1 的真假．
分别写出下列各命题的逆命题，否命题，逆否命题，并判断它们
(1)若a>b且c>d，则a＋c>b＋d (2)(08· 安徽卷改编)若a<0，则方程ax2＋2x＋1＝0至少有一个负数根． 【解析】 (1)逆命题：若a＋c>b＋d，则a>b且c>d(假命题) 否命题：若a≤b或c≤d，则a＋c≤b＋d(假命题) 逆否命题：若a＋c≤b＋d，则a≤b或c≤d(真命题)
高考调研 ·新课标高考总复 习
教材回归
1．下列语句是命题的是________．
①lg2是有理数
②x2＋4x＋4≤0 ③在新课标教材中，“简易逻辑”是必修内容
④2010年7月1日是中国共产党90岁生日吗？
⑤请给我一本衡水重点中学内部学案《高考调研》！ 答案 ① ③
高考调研 ·新课标高考总复 习 2．(2010· 天津卷)命题“若f(x)是奇函数，则f(－x)是奇函数”的否命题是 ( ) A．若f(x)是偶函数，则f(－x)是偶函数 B．若f(x)不是奇函数，则f(－x)不是奇函数 C．若f(－x)是奇函数，则f(x)是奇函数 D．若f(－x)不是奇函数，则f(x)不是奇函数 答案 B 解析 否命题是既否定题设又否定结论．因此否命题应为“若函数f(x)不是 奇函数，则f(－x)不是奇函数”．
年的新课标高考题多为对充要条件的考察，少数涉及到四 种命题及其真假的判断.
高考调研 ·新课标高考总复 习
课前自助餐
课本导读
1．命题 用语言、符号或式子表达的，可以判断真假的陈述句叫做命题． 2．四种命题及其关系 (1)原命题为“若p则q”，则它的逆命题为若q则p；否命题为若┐p则
┐q；逆否命题为若┐q则┐p.
以a>0是|a|>0的充分不必要条件，故选A.
高考调研 ·新课标高考总复 习
授人以渔
题型一 四种命题及其真假的判断
例1 分别写出下列命题的逆命题、否命题、逆否命题，并判断它们的 真假． (1)面积相等的两个三角形是全等三角形． (2)若q<1，则方程x2＋2x＋q＝0有实根． (3)若x2＋y2＝0，则实数x，y全为零． 【解析】 (1)逆命题：全等三角形的面积相等．真命题． 否命题：面积不相等的两个三角形不是全等三角形．真命题．
第二课时命题及其关系、充要条件
高考调研 ·新课标高考总复 习
2011· 考纲下载
1．理解命题的概念．
2．了解“若p，则q”形式的命题及其逆命题、否命
题与逆否命题，会分析四种命题的相互关系． 3．理解必要条件、充分条件与充要条件的意义．
高考调研 ·新课标高考总复 习
请注意！
以选择或填空题为主要题型，一般为容易或中等题，近两
高考调研 ·新课标高考总复 习
பைடு நூலகம்
探究1 ①此类题应先把原命题改写成“若p，则q“的形式，然后再写
出其他命题． 对于含有大前提的命题，在改写命题形式时，大前提不要动．
②若说明命题为真，必须证明．若说明为假，只需举出一个反例即可．
③否命题是难点，注意量词和逻辑联结词．
高考调研 ·新课标高考总复 习
思考题1 分别写出下列各命题的逆命题，否命题，逆否命题，