当前位置：文档之家 › 无限长单位脉冲响应滤波器设计剖析

无限长单位脉冲响应滤波器设计剖析

  • 格式：doc
  • 大小：65.50 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

有限长单位脉冲响应(FIR)滤波器的设计方法-第一节

有限长单位脉冲响应(FIR)滤波器的设计方法-第一节

在通信系统中的应用
信号调制与解调
频分复用
FIR滤波器在通信系统的信号调制与解 调过程中起到关键作用，能够实现信 号的频谱搬移。
FIR滤波器可以实现频分复用，将多个 信号调制到不同的频段上，实现多路 信号同时传输。
信道均衡
在通信过程中，信号经过信道时会受 到各种干扰和失真，FIR滤波器可以用 于信道均衡，减小信号失真。
特点
稳定性好、易于实现、无递归结 构、相位线性等。
FIR滤波器的应用领域
01
02
03
信号处理
FIR滤波器广泛应用于信 号去噪、滤波、增强等处 理。
图像处理
在图像处理中，FIR滤波 器用于图像平滑、锐化等 操作。
通信系统
FIR滤波器用于通信系统 的调制、解调、信道均衡 等。
FIR滤波器与IIR滤波器的比较
群时延
群时延
群时延是描述滤波器对信号延迟影响 的参数。在通信和音频处理中，群时 延的稳定性非常重要，在设计FIR 滤波器时考虑使用特定的窗函数或优 化算法，以减小信号通过滤波器时的 延迟。
幅度响应
幅度响应
幅度响应描述了滤波器对不同频率信号的衰减程度。理想的幅度响应应该是对 所有频率成分具有相同的衰减，但在实际中很难实现。
VS
总结词：计算量较小，需要较高的存 储空间和通信开销，适用于大规模数 据和分布式系统。
05
FIR滤波器的应用实例
在音频处理中的应用
音频信号降噪
FIR滤波器能够有效地去除 音频信号中的噪声，提高 音频质量。
音频压缩
通过FIR滤波器对音频信号 进行压缩，可以减小音频 文件的大小，便于存储和 传输。
最优化方法
最优化方法是一种基于数学优化的FIR滤波器设计方法， 其基本思想是通过优化算法来求解FIR滤波器的系数，

无限长单位脉冲响应IIR滤波器的设计

无限长单位脉冲响应IIR滤波器的设计

无限长单位脉冲响应IIR 滤波器的设计一．设计目的1．掌握数字滤波器的设计过程；2．了解IIR 的原理和特性；3．熟悉设计IIR 数字滤波器的原理和方法；4．学习IIR 滤波器的DSP 实现原理；5．学习使用CCS 的波形观察窗口观察输入/输出信号波形和频谱变化情况。

二．设计内容1．通过MATLAB 来设计一个低通滤波器，对它进行模拟仿真确定IIR 滤波器系数。

2．用DSP 汇编语言及C 语言进行编程，实现IIR 运算，对产生的合成信号，滤除信号中高频成分，观察滤波前后的波形变化。

三．设计原理IIR 滤波器与FIR 滤波器相比具有相位特性差的特点，但它的结构简单，运算量小，具有经济高效的特点，并且可以用较少的阶数获得很高的选择性，因此也得到了广泛的应用。

IIR 数字滤波器系统的传递函数为：H(z)= NN N N z a z a z b z b b z X z Y ----+⋯⋯+++⋯⋯++=111101)()( 它具有N 个极点和N 个零点，如果任何一个极点在单位圆外，则系统不稳定。

如果系数a j （j=1，… ，N ）全部为0，则滤波器变成非递归的FIR滤波器，系统总是稳定的。

对于IIR滤波器，有系数量化敏感的缺点。

由于系统对序列施加的算法是由加法、乘法和延时的基本运算的组合，所以可以用不同结构的数字滤波器来实现而不影响系统总的传输函数。

四．MATLAB设计IIR滤波器的方法我们所用滤波器设计方法为巴特沃夫Butterworth滤波器设计和切比雪夫Chebyshev滤波器设计。

MATLAB的butter函数可以设计低通、带通、高通和带阻数字滤波器，其特征可以使通带内的幅度响应最大限度的平坦，但会损失截止频率处的下降斜度，使幅度响应衰减较慢，因此butter函数主要用于设计通带平坦的数字滤波器。

如果期望幅度响应下降斜度大，衰减快，可以使用Elliptic(椭圆)或Chebyshev(切比雪夫)滤波器。

第3章 无限长单位脉冲响应(IIR)滤波器的设计方法

第3章 无限长单位脉冲响应(IIR)滤波器的设计方法


ˆ H a ( s)



[ha (t ) (t nT )]e
n

st
dt
n
h
ha (t ) (t nT )e st dt
nsT
n
a
(nT )e

n


h(n )e nsT
H ( z)
ut e e u nT e u n e u n
nT 3nT
T n 3T n
1 1 H ( z) 1 T 1 z e 1 z 1e 3T
z (e e ) 1 z 1 (e T e 3T ) e 4T z 2
数字滤波器的设计步骤： 1）按照实际需要确定滤波器的性能要求。 2）用一个因果稳定系统的 H(z) 或 h(n) 去逼近这个 性能要求，即求 h(n) 的表达式。 确定系数 a i 、 bi 或零极点 c i 、 d，以使滤波器 i 满足给定的性能要求——第三章、四章讨论 3）用一个有限精度的运算去实现这个系统函数。包 括 选择运算结构：如级联型、并联型、卷积型、频 率采样型以及快速卷积（FFT）型等; 选择合适的字长和有效数字的处理方法等(第五 章)。
这时数字滤波器的频响才能不失真地重现模拟滤 波器的频响（存在于折叠频率ΩS/2以内）
H (e
j
1 ) Ha ( j ) T T

但任何一个实际的模拟滤波器，其频响都不可能 是真正带限的，因此不可避免地存在频谱的交叠， 即混淆，如图，这时，数字滤波器的频响将不同于 原模拟滤波器的频响而带有一定的失真。模拟滤波 器频响在折叠频率以上衰减越大，失真则越小，这 时，采用脉冲响应不变法设计的数字滤波器才能得 到良好的效果。

有限长单位脉冲响应(FIR)滤波器的设计方法.共84页

有限长单位脉冲响应(FIR)滤波器的设计方法.共84页
44、卓越的人一大优点是：在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联

41、学问是异常珍贵的东西，从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间，才能认识自 己。——德国
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
有限长单位脉冲响应(FIR)滤波器的设 计方法.
6、法律的基础有两个，而且只有两个……公平和实用。——伯克 7、有两种和平的暴力，那就是法律和礼节。——歌德
8、法律就是秩序，有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起，可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的，因为好人用不着它们，而坏人又不会因为它们而变得规矩起来。——德谟耶克斯

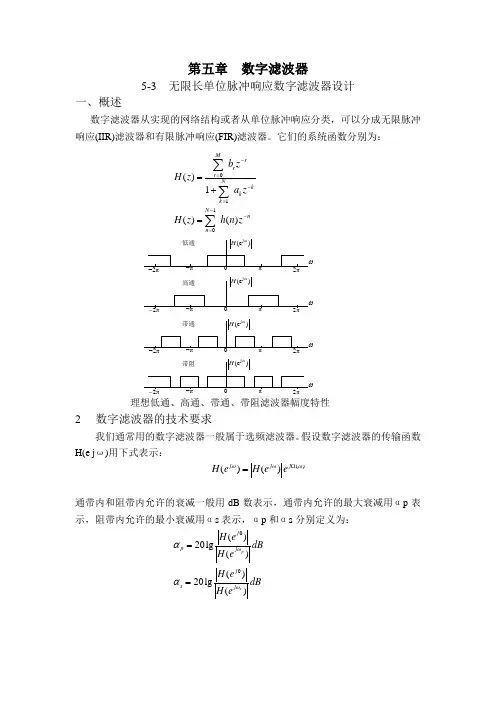
第五章 无限长单位脉冲响应数字滤波器设计

第五章 无限长单位脉冲响应数字滤波器设计

第五章 数字滤波器5-3 无限长单位脉冲响应数字滤波器设计一、概述数字滤波器从实现的网络结构或者从单位脉冲响应分类，可以分成无限脉冲响应(IIR)滤波器和有限脉冲响应(FIR)滤波器。

它们的系统函数分别为：理想低通、高通、带通、带阻滤波器幅度特性2 数字滤波器的技术要求我们通常用的数字滤波器一般属于选频滤波器。

假设数字滤波器的传输函数H(e j ω)用下式表示：通带内和阻带内允许的衰减一般用dB 数表示，通带内允许的最大衰减用αp 表示，阻带内允许的最小衰减用αs 表示，αp 和αs 分别定义为：011()1()()Mrr r Nk kk N nn b z H z a z H z h n z -=-=--==+=∑∑∑)(e j ωH )(e j ωH )(e j ωH )(e j ωH 0低通0高通0带通0带阻ωωωωπ-π2-π2-π2-π-π-π-π-ππππ2π2π2π2()()()j j j H e H e e ωωωΩ=00()20lg ()()20lg()psj p j j s j H e dBH e H e dBH e ωωαα==如将|H(ej0)|归一化为1，则表示成：3. 数字滤波器设计方法概述IIR 滤波器和FIR 滤波器的设计方法是很不相同的。

IIR 滤波器设计方法有两类，经常用的一类设计方法是借助于模拟滤波器的设计方法进行的。

其设计步骤是：先设计模拟滤波器得到传输函数Ha(s)，然后将Ha(s)按某种方法转换成数字滤波器的系统函数H(z)。

二、模拟滤波器的设计模拟滤波器的理论和设计方法已发展得相当成熟，且有若干典型的模拟滤波器供我们选择，如巴特沃斯(Butterworth)滤波器、切比雪夫(Chebyshev)滤波器、椭圆(Cauer)滤波器、贝塞尔(Bessel)滤波器等，这些滤波器都有严格的设计公式、现成的曲线和图表供设计人员使用。

图5-21理想滤波器的幅频特性1.模拟低通滤波器的设计指标及逼近方法模拟低通滤波器的设计指标有αp, Ωp,αs 和Ωs 。

第三章无限长单位脉冲响应滤波器的设计方法

第三章无限长单位脉冲响应滤波器的设计方法
1 H(a s)
12s2s2s3 以 s / c代替其归一化频率，得：
1 H a(s)12(s/ c)2(s/ c)2(s/ c)3
也可以查表得到。由手册中查出巴特沃兹多项式 的系数，之后以 s / c 代替归一化频率，即得 Ha(s)。
将 c 2fc 代入，就完成了模拟滤波器的设计
，但为简化运算，减小误差积累，fc数值放到数字滤 波变换后代入。
为进行脉冲响应不变法变换，计算Ha(S)分母多项式的根， 将上式写成部分分式结构：
c c / 3 e j/6
c / 3 e j/6
H (s )a

s cs c ( 1 j3 )/2s c ( 1 j3 )/2
例1 设采样周期 T25s0 (fs4kh)z,设计一个三阶巴特沃
兹LP滤波器,其3dB截止频率fc=1khz。分别用脉冲响应不变法 和双线性变换法求解。
解：a. 脉冲响应不变法 由于脉冲响不变法的频率关系是线性的，所以可直接按Ωc
=2πfc设计Ha(s)。根据上节的讨论，以截止频率Ωc 归一化的三 阶巴特沃兹 滤波器的传递函数为：
第三章无限长单位脉冲响应滤 波器的设计方法
下面举例讨论应用模拟滤波器低通原型，设计各种数字滤 波器的基本原理，着重讨论双线性变换法。
一．低通变换 通过模拟原型设计数字滤波器的四个步骤：
1）确定数字滤波器的性能要求，确定各临界频率{ωk}。 2）由变换关系将{ωk}映射到模拟域，得出模拟滤波器的临 界频率值{Ωk}。 3）根据{Ωk}设计模拟滤波器的Ha(s) 4） 把Ha(s) 变换成 H(z)（数字滤波器传递函数）
2 2 z 1 1 2 z 1 z 2

河海大学-通信工程-DSP实验4

河海大学-通信工程-DSP实验4

实验四无限长单位脉冲响应滤波器设计班级：姓名：学号：一、实验目的1、掌握双线形变换法及脉冲响应不变法设计IIR数字滤波器的具体设计方法及其原理，熟悉用双线形变换法及脉冲响应不变法设计低通，高通和带通IIR数字滤波器的计算机编程。

2、观察双线形变换法及脉冲响应不变法设计的滤波器的频域特性，了解双线形变换法及脉冲响应不变法的特点。

3、熟悉巴特沃思滤波器，切比雪夫滤波器和椭圆滤波器的频率特性。

；二、实验原理1、将模拟滤波器的参数指标通过频率变换转换为原型模拟低通滤波器的参数指标，设计满足指标要求的原型模拟低通滤波器，通过频率变换将原型模拟低通滤波器的系统函数变换为其他类型的模拟滤波器2、脉冲响应不变法是使数字滤波器的单位脉冲响应序列h（n）逼近模拟滤波器的冲激响应hs（t），让h（n）正好等于hs（t）的采样值。

3、双线性变换法使得s平面与z平面是一一映射关系，消除了多值变换性，克服了脉冲响应不变法产生的频响的混叠失真。

4、巴特沃思滤波器通带内有最大平坦的幅度特性且随着频率的升高而单调的下降和切比雪夫滤波器逼近误差峰值在一个规定的频段上位最小。

三、实验内容1、fc=0.3kHz,δ=0.8dB,fr=0.2kHz,At=20dB,T=1ms;设计一切比雪夫高通滤波器，观察其通带损耗和阻带衰减是否满足要求。

2、fc=0.2kHz, δ=1dB,fr=0.3kHz,At=25dB,T=1ms;分别用脉冲响应不变法及双线形变换法设计一巴特沃思数字低通滤波器，观察所设计数字滤波器的幅频特性曲线，记录带宽和衰减量，检查是否满足要求。

比较这两种方法的优缺点。

3、利用双线性变换法分别设计满足下列指标的巴特沃思滤波器，切比雪夫滤波器和椭圆滤波器，并作图验证设计结果：fc=1.2kHz, δ<=0.5dB,fr=2kHz,At>=40dB,fs=8kHz。

4、分别用脉冲响应不变法及双线形变换法设计一巴特沃思数字带通滤波器，已知fs=3kHz，其等效的模拟滤波器指标为δ<3kHz, 2kHz<f<=3kHz, At>=5dB, f>=6kHz, At>=20dB,f<=1.5kHz。

第四章有限长单位脉冲响应滤波器设计1

第四章有限长单位脉冲响应滤波器设计1

2
2
2
，因而
。这种
线性相位情况和前一种不同之处是，除了产生线性
相位外，还有 2 的固定相移。
0
2 0
2
2
(N 1)
(N 0.5)
h(n) 偶对称
h(n) 奇对称
图1 线性相位特性
二、 线性相位FIR滤波器的幅度特性
分四种情况: 1、h(n)偶对称、
N为偶数 2、h(n)偶对称
N为奇数
且充分条件，它要求单位冲击响应的h（n）序列
以n (N 1)/ 2
h(n) 为偶对称中心，此时，时(N间延1)迟/ 2
等于
长度N-1的一半，即
个
抽样周期。N为偶数时，延时为整数，N为奇数时，
延时等于整h(n数) 加半个抽样周n期 (。N不管1)N/ 2为奇偶，此
时 都应满足对
轴呈偶对称。
另外一种情况是，除了上述的线性相位外，还有一附 加的相位，即
= 2- (cosω+cos2ω)
4、小结：
•四种FIR数字滤波器的相位特性只取决于h(n)的 对称性，而与h(n)的值无关。 •幅度特性取决于h(n)。 •设计FIR数字滤波器时，在保证h(n)对称的条件 下，只要完成幅度特性的逼近即可。
注意：当H(ω)用│H(ω)│表示时，当H(ω)为奇对 称时，其相频特性中还应加一个固定相移π。
2
N 3
2
hn
e jn e jN 1n
h
N
1 e
j
N 1 2
n0
2
H (e
j
)
j
e
N 1 2
N 3 2
h
n0
n
j n N 1

无限长单位脉冲响应滤波器的设计方法共158页文档

无限长单位脉冲响应滤波器的设计方法共158页文档

41、学问是异常珍贵的东西，从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
无限长单位脉冲响应滤波器的设计方
法
21、没有人陪你走一辈子，所以你要 适应孤 独，没 有人会 帮你一 辈子， 所以你 要奋斗 一生。 22、当眼泪流尽的时候，留下的应该 是坚强 。 23、要改变命运，首先改变自己。
24、勇气很有理由被当作人类德性之 首，因 为这种 德性保 证了所 有其余 的德性 。--温 斯顿． 丘吉尔 。 25、梯子的梯阶从来不是用来搁脚的 ，它只 是让人 们的脚 放上一 段时间 ，以便 让别一 只脚能 够再往 上登。
42、只有在人群中间，才能认识自 己。——德国
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一Biblioteka 优点是：在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联

第4章无限长单位脉冲响应(IIR)滤波器的设计方法详解

第4章无限长单位脉冲响应(IIR)滤波器的设计方法详解
1 A( ) 2
2
H j
1 2
,幅度衰减
振幅平方函数的极点：
1 H a ( S ) H a ( S ) S 2N 1 ( ) j c
令分母为零，得
S P (1)
1 2N
( jc )
2 k 1 j 2 N 2
SP (e
j 2 k 1
r 100.1 At 1 2 N lg lg 100.1 1 1
100.1 At 1 lg 1 100.1 1 N 2 r lg 1
2. 确定Ωc
1 c
2N
10
2N
0.1
H j
H j
c O c

c O c

模拟低通滤波器AF LP
H j
模拟高通滤波器AF HP
H j
1 2 O 2
1

1 2 O 2
1

模拟带通滤波器AF BP
模拟带阻滤波器AF BS
H e j

H e j
4.1 滤波器的基本原理
滤波：滤除信号中不需要的分量，保留有用的分量。
离散系统的数字模型： yn bi yn i ai xn i
i 1 i 0 N M
离散系统的系统函数：
H z
i a z i i 0
M
1 bi z i
i 1
N
)
1 2N
(e 2 c ) e
j

c 1 k 2N
Butterworth滤波器 的振幅平方函数有2N个极 点，它们均匀对称地分布在|S|=Ωc的圆周上。

无限长单位脉冲响应(IIR)滤波器设计(2)

无限长单位脉冲响应(IIR)滤波器设计(2)
0

式中ha(t)为系统的冲激响应，是实函数。

∴ 不难看出
H a ( j) ha (t )cost j sin t dt
0
H a ( j) H a ( j)
定义振幅平方函数
A( 2 ) H a ( j) H a ( j) H a ( j) 2
振幅平方函数为
A( ) H a ( j)
2
2
1 1 V ( ) c
2 2 N
—与通带波纹有关的参量， 大 ，波纹大。 0 < <1
VN（x）—N阶切比雪夫多项式，定义为
1 cos( N cos x) VN ( x) 1 cosh( N cosh x)
c —有效通带截止频率
x 1 x 1
x 1时, VN ( x ) 1 x 1, x , VN ( x )
如图1,通带内
1 c
H a ( j )
2
1 变化范围1~ 1 2
Ω＞Ωc
，随Ω/Ωc
↗，
H a ( j ) 0 (迅速趋于零) →
2
当 Ω =0时，
H a ( j) 0
c
1 A(0) 2
,幅度衰减 1 ，相当
2
振幅平方函数的极点：
1 H a ( S ) H a ( S ) S 2N 1 ( ) j c
令分母为零，得
S P (1)
1 2N
( j c )
可见，Butter worth滤波器 的振幅平方函数有2N个极 点，它们均匀对称地分布在|S|=Ωc的圆周上。 例：为N=3阶BF振幅平方函数的极点分布，如图。
2
1 2 1 cos[N arccos(0)]

无限长单位脉冲响应滤波器设计剖析

无限长单位脉冲响应滤波器设计剖析

实验四无限长单位脉冲响应滤波器设计一、实验目的1.掌握双线性变换法及脉冲响应不变法设计IIR数字滤波器的具体设计方法及其原理，熟悉用双线性变换法及脉冲响应不变法设计低通、高通和带通IIR数字滤波器的计算机编程。

2.观察双线性变换及脉冲响应不变法设计的滤波器的频率特性，了解双线性变换法及脉冲响应不变法的特点。

3.熟悉巴特沃思滤波器、切比雪夫滤波器和椭圆滤波器的频率特性。

二、实验原理(1)实验中有关变量的定义：fc通带边界频率，fr阻带边界频率，tao通带波动，at 最小阻带衰减，fs采样频率，t采样周期。

(2)设计一个数字滤波器一般包括以下两步：a.按照任务要求，确定滤波器性能指标b.用一个因果稳定的离散时不变系统的系统函数去逼近这一性能要求(3)数字滤波器的实现：对于IIR滤波器，其逼近问题就是寻找滤波器的各项系数，使其系统函数逼近一个所要求的特性。

先设计一个合适的模拟滤波器，然后变换成满足约定指标的数字滤波器。

用双线形变换法设计IIR数字滤波器的过程：a.将设计性能指标中的关键频率点进行“预畸”b.利用“预畸”得到的频率点设计一个模拟滤波器。

c.双线形变换，确定系统函数三、实验内容1、设计一切比雪夫高通滤波器，性能指标如下：通带边界频率f c=0.4kHz，通带波动δ=0.5dB，阻带边界频率f r=0.3kHz，阻带最小衰减At=20dB，采样频率f s=1000Hz，观察其通带波动和阻带衰减是否满足要求。

（绘制对数幅度谱）2、设计一巴特沃思低通滤波器，性能指标如下：通带边界频率f c=0.4kHz，通带波动δ=1dB，阻带边界频率f r=0.6kHz，阻带最小衰减At=40dB，采样频率f s=2000Hz，分别用脉冲响应不变法和双线性变换法进行设计，比较两种方法的优缺点。

（绘制线性幅度谱）3、用双线性变换法设计巴特沃思、切比雪夫和椭圆低通滤波器，其性能指标如下：通带边界频率f c=1.8kHz，通带波动δ≤1dB，阻带边界频率f r=2.6kHz，阻带最小衰减A t≥50dB，采样频率f s=8kHz。

第3章无限长单位脉冲响应IIR滤波器设计第四节-26页精选文档

第3章无限长单位脉冲响应IIR滤波器设计第四节-26页精选文档
0~~0 0~0~0
0 ~ ， ~
的变化范围为 2 ,故 N=2
又 g(1)=1, 所以，全通函数取正号。
由以上分析得变换关系：
u1g(z1)rz2z22r1rz1z1 1r21
（1）
或
ej re2e2j2jr1er1ejjr21
确定 ：
把变换关系 c c 带入（2）式 ，有：
ejc 1ejcejc
得
sin 式的 ~ 频率关系，如图1(b)
LP-LP频率变换
c c
图1(b) LP-LP频率变换特性
§3.4 从低通数字滤波器到各种数字滤波器的频率变换 （Z平面变换法）
上一节讨论了由模拟网络的低通原型来设计各种DF的方 法，这种原型变换的设计方法同样也可直接在数字域上进行。
DF低通原型函数 Hp(z)变 换各种DF的 H（z）
这种变换是由 个映射变换。
H p (Z)
所在的Z平面到H（z）所在的Z平面的一
G ( z 1 ) 的所有零点 1/i* 都是其极点的共轭倒数
N：全通函数的阶数。
0 变化时，相位函数 的变化量为N 。
不同的N和 i 对应 各类不同的变换。
下面具体讨论几种原型变换：
① 低通——低通（LP）
LP→LP的变换中，Hp(ej )和 Hej都是低通函
其中 是实数，且 1


0



0
c
图1(a) LP-LP变换（有对称性）
将 zej及 uej代入上式，可得到上述变换所反映的频率
变换关系：
ej 1ejej
（2）
由此得
12sin
arctan

【2019年整理】CH3无限长单位脉冲响应滤波器IIR的设计方法

【2019年整理】CH3无限长单位脉冲响应滤波器IIR的设计方法

Slide 3
设计数字滤波器的步骤：
• 一般包括以下三步： • (1)按照任务的要求，确定滤波器的性能 指标任务包括：
°需要滤除哪些频率分量 °保留哪些频率分量 °保留的部分允许有多大的幅度或相位失真
• •
Slide 4
(2)用一个因果稳定的离散线性时不变系 统的系统函数去逼近这一性能要求 系统函数可以分为IIR和FIR两类系统
• 该方法只适用于带限的AF。
• 高通和带阻滤波器不宜采用脉冲响 应不变法

否则要加保护滤波器，滤掉高于折叠 频率以上的分量。
阻带衰减越大，则混叠效应越小
• 带通和低通滤波器，需充分地带限

Slide 24
例1 将已知传递函数的模拟滤波器数字化
图3.3 脉冲响应不变法的幅频特性
Slide 25
3.1.2 双线性变换法 P105
M
一般M N
Slide 7
系统的组成
•一般，M≤N,这类系统称为N阶系统
•当 M ＞ N 时， H(z) 可看成是一个 N 阶 IIR 子系统与一个 (M-N) 阶的 FIR 子系 统的级联。
X(n)
IIR
(N阶)
FIR
(M-N阶)
y(n)
Slide 8
数字低通滤波器频率响应幅度特性的容限图
H (e j )
1＋ 1 1 1－ 1 通带 过渡带 阻带
2
o
1 1 | H (e j ) | 1 1
| H (e j ) | 2
Slide 9
|ω|≤ωc ωr≤|ω|≤π
IIR滤波器的逼近问题
• 寻找滤波器的各系数 ai 和 bi，使其逼 近一个所要求的特性。 • 通常有以下两种方法：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

实验四无限长单位脉冲响应滤波器设计一、实验目的1.掌握双线性变换法及脉冲响应不变法设计IIR数字滤波器的具体设计方法及其原理，熟悉用双线性变换法及脉冲响应不变法设计低通、高通和带通IIR数字滤波器的计算机编程。

2.观察双线性变换及脉冲响应不变法设计的滤波器的频率特性，了解双线性变换法及脉冲响应不变法的特点。

3.熟悉巴特沃思滤波器、切比雪夫滤波器和椭圆滤波器的频率特性。

二、实验原理(1)实验中有关变量的定义：fc通带边界频率，fr阻带边界频率，tao通带波动，at 最小阻带衰减，fs采样频率，t采样周期。

(2)设计一个数字滤波器一般包括以下两步：a.按照任务要求，确定滤波器性能指标b.用一个因果稳定的离散时不变系统的系统函数去逼近这一性能要求(3)数字滤波器的实现：对于IIR滤波器，其逼近问题就是寻找滤波器的各项系数，使其系统函数逼近一个所要求的特性。

先设计一个合适的模拟滤波器，然后变换成满足约定指标的数字滤波器。

用双线形变换法设计IIR数字滤波器的过程：a.将设计性能指标中的关键频率点进行“预畸”b.利用“预畸”得到的频率点设计一个模拟滤波器。

c.双线形变换，确定系统函数三、实验内容1、设计一切比雪夫高通滤波器，性能指标如下：通带边界频率f c=0.4kHz，通带波动δ=0.5dB，阻带边界频率f r=0.3kHz，阻带最小衰减At=20dB，采样频率f s=1000Hz，观察其通带波动和阻带衰减是否满足要求。

（绘制对数幅度谱）2、设计一巴特沃思低通滤波器，性能指标如下：通带边界频率f c=0.4kHz，通带波动δ=1dB，阻带边界频率f r=0.6kHz，阻带最小衰减At=40dB，采样频率f s=2000Hz，分别用脉冲响应不变法和双线性变换法进行设计，比较两种方法的优缺点。

（绘制线性幅度谱）3、用双线性变换法设计巴特沃思、切比雪夫和椭圆低通滤波器，其性能指标如下：通带边界频率f c=1.8kHz，通带波动δ≤1dB，阻带边界频率f r=2.6kHz，阻带最小衰减A t≥50dB，采样频率f s=8kHz。

（绘制对数幅度谱）4、设计一巴特沃思带通滤波器，性能指标如下：通带频率3kH z≤f≤4kHz，通带波动δ≤1dB；上阻带f≥5kHz，阻带最小衰减At≥15dB；下阻带f≤2kHz，阻带最小衰减At≥20dB；采样频率f s=20kHz，分别用脉冲响应不变法和双线性变换法进行设计。

（绘制线性幅度谱）5、用双线性变换法设计一椭圆带阻滤波器，性能指标如下：阻带频率2kH z≤f≤3kHz，阻带最小衰减At ≥30dB ，通带频率f ≥4kHz 和f ≤1k Hz ，通带波动δ≤3dB ，采样频率f s =10kHz 。

（绘制对数幅度谱）注意：设计结果要求给出程序、数字滤波器的系统函数()H z 和幅频响应，()H z 请用word 自带的公式编辑器编辑（插入－对象－Microsoft 公式3.0）。

四、实验结果与分析1.实验结果：-30-25-20-15-10-55频率/Hz幅度/d B切比雪夫高通滤波器程序：fs=1000;fc=400;fr=300;rp=0.5;rs=20; ws=2*fs*tan(2*pi*fc/fs/2); wp=2*fs*tan(2*pi*fr/fs/2);[N,wn]=cheb1ord(wp,ws,rp,rs,'s'); [b,a]=cheby1(N,rp,wp,'high','s'); [bz,az]=bilinear(b,a,fs); [h,w]=freqz(bz,az); f=w/2/pi*fs; figure;plot(f,20*log10(abs(h))); axis([0,500,-30,5]); grid;xlabel('频率/Hz'); ylabel('幅度/dB');title('切比雪夫高通滤波器');实验结果分析：由图像观察可知，通带波动为0.5dB ，阻带最小衰减20dB,满足要求。

2.实验结果：00.20.40.60.811.21.4频率/Hz幅度巴特沃思低通滤波器，线性幅度谱程序：fs=2000;fc=400;fr=600;rp=1;rs=40; %脉冲响应不变法 wp=2*pi*fc; ws=2*pi*fr;[N,wn]=buttord(wp,ws,rp,rs,'s'); [b1,a1]=butter(N,wn,'s');[bz1,az1]=impinvar(b1,a1,fs); [h1,w]=freqz(bz1,az1); %双线性变换法wp=2*fs*tan(2*pi*fc/fs/2); ws=2*fs*tan(2*pi*fr/fs/2);[N,wn]=buttord(wp,ws,rp,rs,'s'); [b2,a2]=butter(N,wn,'s'); [bz2,az2]=bilinear(b2,a2,fs); [h2,w]=freqz(bz2,az2); f=w/(2*pi)*fs; figure;plot(f,abs(h1),'-.r',f,abs(h2),'-b');%线性幅度谱 grid;xlabel('频率/Hz'); ylabel('幅度');legend('脉冲响应不变法','双线性变换法'); title('巴特沃思低通滤波器，线性幅度谱');实验结果分析：脉冲响应不变法由于混碟效应，使得过渡带和阻带的衰减特性变差，并且不存在传输零点。

同时，也看到双线性变换法，在f=1000Hz 处有一个三阶传输零点，这个三阶零点正是模拟滤波器在Ω=无穷大处的三阶传输零点通过映射形成的。

3.实验结果：-80-70-60-50-40-30-20-10010频率/Hz幅度/d B巴特沃思低通滤波器-80-70-60-50-40-30-20-10010频率/Hz幅度/d B切比雪夫低通滤波器-80-70-60-50-40-30-20-10010频率/Hz幅度/d B椭圆滤波器程序：(1) fs=8000;fc=1800;fr=2600;rp=1;rs=50; wp=2*fs*tan(2*pi*fc/fs/2); ws=2*fs*tan(2*pi*fr/fs/2);[N,wn]=buttord(wp,ws,rp,rs,'s'); [b,a]=butter(N,wn,'s'); [bz,az]=bilinear(b,a,fs); [h,w]=freqz(bz,az); f=w/pi/2*fs; figure;plot(f,20*log10(abs(h1))); axis([0,8000,-80,10]); grid;xlabel('频率/Hz'); ylabel('幅度/dB');title('巴特沃思低通滤波器');(2) fs=8000;fc=1800;fr=2600;rp=1;rs=50; wp=2*fs*tan(2*pi*fc/fs/2); ws=2*fs*tan(2*pi*fr/fs/2);[N,wn]=cheb1ord(wp,ws,rp,rs,'s'); [b,a]=cheby1(N,rp,wp,'s'); [bz,az]=bilinear(b,a,fs); [h,w]=freqz(bz,az); f=w/pi/2*fs; figure;plot(f,20*log10(abs(h))); axis([0,6000,-80,10]);grid;xlabel('频率/Hz'); ylabel('幅度/dB');title('切比雪夫低通滤波器');(3) fs=8000;fc=1800;fr=2600;rp=1;rs=50;wp=2*fs*tan(2*pi*fc/fs/2); ws=2*fs*tan(2*pi*fr/fs/2);[N,wp]=ellipord(wp,ws,rp,rs,'s'); [b,a]=ellip(N,rp,rs,wp,’s'); [bz,az]=bilinear(b,a,fs); [h,w]=freqz(bz,az); f=w/pi/2*fs; figure;plot(f,20*log10(abs(h))); axis([0,6000,-80,10]); grid;xlabel('频率/Hz'); ylabel('幅度/dB'); title('椭圆滤波器');实验结果分析：由图像可知，巴特沃思滤波器的特点是具有通带内最平坦的幅度特性，而且随着频率的升高而单调地下降；切比雪夫滤波器的特点是其逼近误差峰值在一个规定的频段的频段上为最小，实际上误差值在规定的频段上是等波纹的，即误差值等幅地在极大值和极小值之间摆动；椭圆滤波器的特点是其幅值响应在通带和阻带内都是等波纹的，对于给定的阶数和给定的波纹要求，除椭圆滤波器外，其他滤波器均不能获得较窄的过渡带宽。

4.实验结果：00.20.40.60.811.21.4频率/Hz幅度巴特沃思带通滤波器，线性幅度谱程序：fs=20000;fc=[3000 4000];fr=[2000 5000];rp=1;rs=20; %脉冲响应不变法 wp=2*pi*fc; ws=2*pi*fr;[N,wn]=buttord(wp,ws,rp,rs,'s'); [b1,a1]=butter(N,wn,'s');[bz1,az1]=impinvar(b1,a1,fs); [h1,w]=freqz(bz1,az1); %双线性变换法wp=2*fs*tan(2*pi*fc/fs/2); ws=2*fs*tan(2*pi*fr/fs/2);[N,wn]=buttord(wp,ws,rp,rs,'s'); [b2,a2]=butter(N,wn,'s'); [bz2,az2]=bilinear(b2,a2,fs); [h2,w]=freqz(bz2,az2); f=w/(2*pi)*fs; figure;plot(f,abs(h1),'-.r',f,abs(h2),'-b');%线性幅度谱 grid;xlabel('频率/Hz'); ylabel('幅度');legend('脉冲响应不变法','双线性变换法'); title('巴特沃思带通滤波器，线性幅度谱');实验结果分析：脉冲响应不变法由于混碟效应，使得过渡带和阻带的衰减特性变差，并且不存在传输零点。