专题(八) 构造“三线合一”巧解题(选用)

北师大版初二数学下册《活用“三线合一” 巧解题》讲义【名师点睛】等腰三角形〝顶角均分线、底边上的高、底边上的中线〞只需知道此中〝一线〞，就能够说明是其余〝两线〞。

运用等腰三角形〝三线合一〞的性质证明角相等、线段相等或垂直关系，能够减少证明全等的次数，简化解题过程。

[ 技巧 1]利用〝三线合一〞求角1.如图 ,房子的顶角∠ BAC=100°，过屋顶 A 的立柱 AD ⊥BC，屋椽 A B=AC ，求顶架上∠ B、∠ C、∠ BAD 、∠ CAD 的度数。

解答：∵△ ABC 中,AB=AC, ∠BAC=100°∴∠ B=∠C= 1°∠BAC)=1(180°°°2(180 -2- 100 )=40∵A B=AC,AD ⊥BC,∠BAC=100°∴AD 均分∠ BAC∴∠ BAD= ∠CAD=50.[ 技巧 2]利用〝三线合一〞求线段2.如图，在△ ABC 中，AB=AC ，AD=DB=BC ，DE⊥AB 于点 E，假定CD=4，且△ BDC 的周长为 24，求 AE 的长。

解答：∵A D=DB=BC ，CD=4，且△ BDC 的周长为 24∴A D=DB=BC=10∴A C=14∵A B=AC∴A B=14∵A D=DB ，DE⊥AB∴A E=BE= 1AB=7. 2[ 技巧 3]利用〝三线合一〞证全等3.：三角形 ABC 中,∠A=90°，AB=AC ，D 为 BC 的中点，如图， E， F 分别是 AB ，AC 上的点，且 BE=AF ，求证：△ DEF 为等腰直角三角形。

解答：证明：连结 AD∵A B=AC, ∠ A=90°，D 为 BC 中点∴AD=BC2=BD=CD且 AD 均分∠ BAC∴∠ BAD= ∠CAD=45 °在△ BDE 和△ ADF 中， BD=AD ，∠ B=∠DAF=45 °，BE=AF ∴△ BDE≌△ ADF∴D E=DF ，∠ BDE=∠ADF∵∠ BDE+ ∠ADE=90 °∴∠ ADF+ ∠ADE=90 °即：∠ EDF=90°∴△ EDF 为等腰直角三角形。

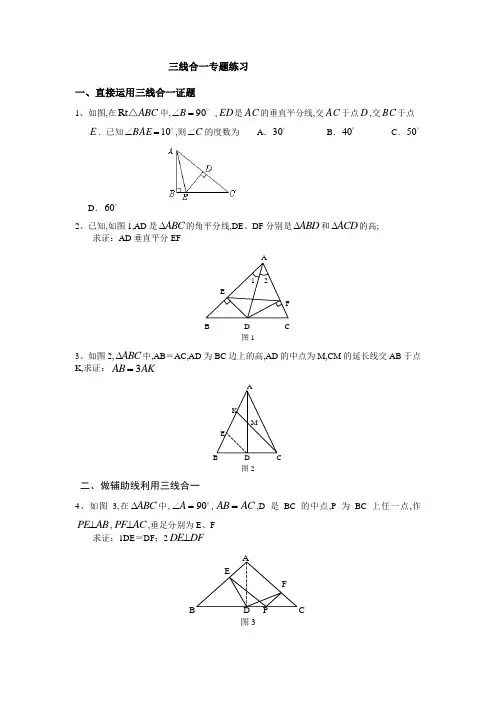
三线合一专题练习
一、直接运用三线合一证题
1、如图,在Rt ABC △中,
90=∠B ,ED 是AC 的垂直平分线,交AC 于点D ,交BC 于点E ．已知 10=∠BAE ,则C ∠的度数为 A ． 30 B ． 40 C ． 50
D ． 60
2、已知,如图1,AD 是∆ABC 的角平分线,DE 、DF 分别是∆ABD 和∆ACD 的高; 求证：AD 垂直平分EF
A
1 2
E
F
B D C
图1
3、如图2,∆ABC 中,AB ＝AC,AD 为BC 边上的高,AD 的中点为M,CM 的延长线交AB 于点K,求证：AB AK =3
A
K
M
E
图2
二、做辅助线利用三线合一
4、如图3,在∆ABC 中,∠=A 90
,AB AC =,D 是BC 的中点,P 为BC 上任一点,作PE AB ⊥,PF AC ⊥,垂足分别为E 、F
求证：1DE ＝DF ；2DE DF ⊥ A
E
F
B D P 图3
5、如图,在等腰梯形ABCD中,G为对角线交点,△ADG、△GBC为正三角形;F、E、H为AG、BG、DC的中点; 连接CE BF
1求证：△EFH为正三角形；
2若AD=2,BG=3,求S△EFH；
ACB ADB90 ,M、N分别为AB、CD的中点,求6、如图4,已知四边形ABCD中,∠=∠=
⊥
证：MN CD
C
N
D
A M B
图4
7、如图,已知在等边三角形ABC中,D是AC的中点,E为BC延长线上一点,且CE＝CD,DM ⊥BC,垂足为M;求证：M是BE的中点;
A
D
1
B M
C E。

正多边形三线合一专项综合练习本文档旨在提供正多边形三线合一综合练的相关内容。

以下是几个题例以供参考。

问题1：正三角形的三线合一问题假设有一个正三角形ABC，其中A、B、C分别代表三个角。

现在要求证明三角形内的三条特殊线段AA'、BB'、CC'共点于一个点O，即三线合一。

对于正三角形ABC来说，我们可以通过几何推导来证明三线合一的问题。

具体证明过程如下：1. 连接BC、AC、AB，得到线段AA'、BB'、CC'；2. 在AB上任意取一点D，连接CD；3. 观察△ACD和△BCD，通过对角线法则和对边法则，可以得出△ACD与△BCD相似；4. 由于△ACD与△BCD相似，我们可以推导出DD'与BB'比例一致；5. 同理，可以推导出AA'与DD'比例一致；6. 因此，根据比例定理，我们可以得到AA'与BB'的延长线与CC'的交点为O，即证明了正三角形的三线合一问题。

问题2：正方形的三线合一问题假设有一个正方形ABCD，其中A、B、C、D分别代表四个角。

现在要求证明三线合一。

对于正方形ABCD来说，我们可以通过以下几个步骤来证明三线合一问题：1. 连接AC，得到线段AA'；2. 连接BD，得到线段BB'；3. 连接AD和BC，得到线段CC'；4. 线段AA'、BB'的延长线与线段CC'的交点为O，即证明了正方形的三线合一问题。

问题3：正六边形的三线合一问题假设有一个正六边形ABCDEF，其中A、B、C、D、E、F分别代表六个角。

现在要求证明三线合一。

对于正六边形ABCDEF来说，我们可以通过以下几个步骤来证明三线合一问题：1. 连接CD和FA，得到线段AA'；2. 连接CE和FB，得到线段BB'；3. 连接CF和AE，得到线段CC'；4. 线段AA'、BB'的延长线与线段CC'的交点为O，即证明了正六边形的三线合一问题。

专训3活用“三线合一”巧解题名师点金：等腰三角形“顶角平分线、底边上的高、底边上的中线”只要知道其中“一线”，就可以说明是其他“两线”．运用等腰三角形“三线合一”的性质证明角相等、线段相等或垂直关系，可减少证全等的次数，简化解题过程．利用“三线合一”求角1．如图，房屋顶角∠BAC＝100°，过屋顶A的立柱AD⊥BC，屋檐AB＝AC.求顶架上的∠B，∠C，∠BAD，∠CAD的度数．(第1题)利用“三线合一”求线段2．如图，在△ABC中，AB＝AC，AD＝DB，DE⊥AB 于点E，若BC＝10，且△BDC的周长为24，求AE的长．(第2题)3．如图，在△ABC中，∠A＝90°，AB＝AC，D为BC 的中点，E，F分别是AB，AC上的点，且BE＝AF，求证：DE＝DF.(第3题)利用“三线合一”证垂直4．如图，在△ABC中，AC＝2AB，AD平分∠BAC，E 是AD上一点，且EA＝EC.求证：EB⊥AB.(第4题)利用“三线合一”证线段的倍数关系(构造三线法)5．如图，在等腰直角三角形ABC中，AB＝AC，∠BAC ＝90°，BF平分∠ABC，CD⊥BF交BF的延长线于点D.求证：BF＝2CD.(第5题)利用“三线合一”证线段的和差关系(构造三线法)6．如图，在△ABC中，AD⊥BC于点D，且∠ABC＝2∠C.求证：CD＝AB＋BD.(第6题)答案1．解：∵AB＝AC，∠BAC＝100°，AD⊥BC，∴∠B ＝∠C＝40°，∠BAD＝∠CAD＝50°.2．解：∵△BDC的周长＝BD＋BC＋CD＝24，BC＝10，∴BD＋CD＝14.∵AD＝BD，∴AC＝AD＋CD＝BD＋CD＝14. ∴AB＝AC＝14.∵AD＝DB，DE⊥AB，∴AE＝EB＝12AB＝7.3．证明：如图，连接AD.∵AB＝AC，D为BC的中点，∴AD⊥BC.∴∠ADB＝90°.∵AB＝AC，∠BAC＝90°，∴∠B＝∠C＝45°.在△ABD中，∠BAD＝180°－∠B－∠ADB＝45°，∴∠B＝∠BAD.∴BD＝AD.又∵BD＝CD，∴AD＝CD.∴∠DAC＝∠C＝45 °.∴∠B＝∠DAF.又∵BE＝AF，∴△BDE≌△ADF(SAS)．∴DE＝DF.(第3题4．证明：如图，过点E作EF⊥AC于F.∵AE＝EC，∴AC ＝2AF.又∵AC＝2AB，∴AF＝AB.∵AD平分∠BAC，∴∠FAE＝∠BAE.又∵AE＝AE，∴△AEF≌△AEB(SAS)．∴∠ABE＝∠AFE＝90°，即EB⊥AB.(第4题) 5．证明：如图，延长BA，CD交于点E.由BF平分∠ABC，CD⊥BD，BD＝BD，易得△BDC≌△BDE.∴BC＝BE.又∵BD⊥CE，∴CE＝2CD.∵∠BAC＝90°，∠BDC＝90°，∠AFB＝∠DFC，∴∠ABF＝∠DCF.又∵AB＝AC，∠BAF＝∠CAE＝90°，∴△ABF≌△ACE(ASA)．∴BF＝CE.∴BF＝2CD.(第5题)6．证明：如图，以A为圆心，AB长为半径画弧交CD 于点E，连接AE，则AE＝AB，所以∠AEB＝∠ABC.因为AD⊥BC，所以AD是BE边上的中线，即DE＝BD.又因为∠ABC＝2∠C，所以∠AEB＝2∠C.而∠AEB＝∠CAE＋∠C，所以∠CAE＝∠C.所以CE＝AE＝AB.故CD＝CE＋DE＝AB＋BD.(第6题)。

专题08解题技巧专题：利用等腰三角形的'三线合一'作辅助线压轴题三种模型全攻略【考点导航】目录【典型例题】 (1)【类型一等腰三角形中底边有中点时，连中线】 (1)【类型二等腰三角形中底边无中点时，作高线】 (4)【类型三巧用“角平分线+垂线合一”构造等腰三角形】 (5)【典型例题】【类型一等腰三角形中底边有中点时，连中线】例题：已知，在ABC 中，90ACB ∠=︒，AC BC =，点M 是AB 的中点，作90DME ∠=︒，使得射线MD 与射线ME 分别交射线AC ，CB 于点D ，E ．(1)如图1，当点D 在线段AC 上时，线段MD 与线段ME 的数量关系是___________；(2)如图2，当点D 在线段AC 的延长线上时，用等式表示线段CD ，CE 和BC 之间的数量关系并加以证明．【变式训练】1．在ABC 中，90A ∠=︒，AB AC =，点D 是边BC 的中点．(1)如图，若点E ，F 分别在边AB ，AC 上，DE DF ⊥，求证：BE AF =，并说明理由；(2)在（1）的条件下，AB AC a ==，求AE AF +的值．2．如图1，在Rt ABC △中，90C ∠=︒，AC BC =，点P 是斜边AB 的中点，点D ，E 分别在边,AC BC 上，连接,PD PE ，若PD PE ⊥．(1)求证：PD PE =；(2)若点D ，E 分别在边,AC CB 的延长线上，如图2，其他条件不变，（1）中的结论是否成立？并加以证明；(3)在（1）或（2）的条件下，PBE △是否能成为等腰三角形？若能，请直接写出PEB ∠的度数（不用说理）；若不能，请说明理由．(1)若90EOF ∠=︒，两边分别交,AC BC 于E ，F 两点．【类型二等腰三角形中底边无中点时，作高线】例题：如图，已知点D 、E 在△ABC 的边BC 上，AB ＝AC ，AD ＝AE ．(1)求证：BD ＝CE ；(2)若AD ＝BD ＝DE ＝CE ，求∠BAE 的度数．【变式训练】1．如图，ADB 与△BCA 均为等腰三角形，AD AB CB ==，且90ABC ∠=︒，E 为DB 延长线上一点，2DAB EAC ∠=∠．(1)若20∠=︒EAC ，求CBE ∠的度数；(2)求证：AE EC ⊥；(3)若BE a =，AE b =，CE c =，求ABC 的面积（用含a ，b ，c 的式子表示）．(1)如图1，若ACD ∠与BAC ∠互余，则DCB ∠=__________(【类型三巧用“角平分线+垂线合一”构造等腰三角形】例题：如图，在ABC 中，AD 平分BAC ∠，E 是BC 的中点，过点E 作FG AD ⊥交AD 的延长线于H ，交AB 于F ，交AC 的延长线于G ．求证：(1)AF AG =；(2)BF CG =．【变式训练】(1)【问题情境】利用角平分线构造全等三角形是常用的方法，如图1，OP 平分MON ∠．点AC OP ⊥，垂足为C ，延长AC 交ON 于点B ，可根据证明AOC ≌△△点C 为AB 的中点）．(2)【类比解答】如图2，在ABC 中，CD 平分ACB ∠，AE CD ⊥于E ，若63EAC ∠=︒，办法，可求得DAE ∠=．(3)【拓展延伸】如图3，ABC 中，AB AC =，90BAC ∠=︒，CD 平分ACB ∠，BE CD ⊥，垂足E 在CD 的延长线上，试探究BE 和CD 的数量关系，并证明你的结论．(4)【实际应用】如图4是一块肥沃的三角形土地，其中AC 边与灌渠相邻，李伯伯想在这块地中划出一块直角三角形土地进行水稻试验，故进行如下操作：①用量角器取ACB ∠的角平分线CD ；②过点A 作AD CD ⊥于D ．已知13BC =，10AC =，ABC 面积为20，则划出的ACD 的面积是多少？请直接写出答案．2．【问题情境】利用角平分线构造全等三角形是常用的方法，如图1，OP 平分MON ∠，点A 为OM 上一点，过点A 作AC OP ⊥，垂足为C ，延长AC 交ON 于点B ，易证AOC ∆≌BOC ∆，则AC BC =．其分析过程如下：在AOC ∆和BOC ∆中，OP 平分MON AOC BOC∠⇒∠=∠90OC OC AC OP OCA OCB =⊥⇒∠=∠=︒，⇒AOC ∆≌BOC ∆（___________）在括号内填写全等判定方法字母简称AC BC ⇒=（___________）在括号内填写理由依据【问题探究】如图2，ABC ∆中，90AB AC BAC CD =∠=︒，，平分ACB BE CD ∠⊥，，垂足E 在CD 的延长线上．证明：2CD BE =；【拓展延伸】。

专训2 “三线合一”解题的六种技巧名师点金：等腰三角形中的“顶角平分线、底边上的高、底边上的中线”只要知道其中“一线”，就可以说明是其他“两线”．运用等腰三角形“三线合一”的性质证明角相等、线段相等或垂直关系，可减少证全等的次数，简化解题过程．利用“三线合一”求角1．如图，房屋顶角∠BAC＝100°，过屋顶A的立柱AD⊥BC，屋檐AB＝AC.求顶架上的∠B，∠C，∠BAD，∠CAD的度数．(第1题)利用“三线合一”求线段2．如图，在△ABC中，AB＝AC，AD＝DB，DE⊥AB于点E，若BC＝10，且△BDC的周长为24，求AE的长．(第2题)利用“三线合一”证线段(角)相等3．已知△ABC中，∠BAC＝90°，AB＝AC，D为BC的中点．(1)如图①，E，F分别是AB，AC上的点，且BE＝AF，试判断△DEF的形状，并说明理由．(2)如图②，若E，F分别为AB，CA的延长线上的点，且仍有BE＝AF.请判断△DEF是否仍有(1)中的形状，并说明理由．(第3题)利用“三线合一”证垂直4．如图，在△ABC中，AC＝2AB，AD平分∠BAC，E是AD上一点，且EA＝EC.求证：EB⊥AB.(第4题)利用“三线合一”证线段的倍数关系(构造三线法)5．如图，已知等腰直角三角形ABC中，AB＝AC，∠BAC＝90°，BF平分∠ABC，CD⊥BD 交BF的延长线于点D.试说明：BF＝2CD.(第5题)利用“三线合一”证线段的和差关系(构造三线法)6．如图，在△ABC中，AD⊥BC于点D，且∠ABC＝2∠C.试说明：CD＝AB＋BD.(第6题)答案1．解：因为AB＝AC，∠BAC＝100°，AD⊥BC，所以∠B＝∠C＝40°，∠BAD＝∠CAD＝50°.2．解：因为△BDC的周长＝BD＋BC＋CD＝24，BC＝10，所以BD＋CD＝14.∵AD＝BD，∴AC＝AD＋CD＝BD＋CD＝14.又∵AB＝AC＝14.AD＝DB，DE⊥AB，∴AE ＝EB ＝12AC ＝7. 3．解：(1)△DEF 为等腰直角三角形．理由：连接AD ，易证△BDE ≌△ADF ，∴DE ＝DF ，∠BDE ＝∠ADF ，又∵∠BAC ＝90°，AB ＝AC ，D 为BC 的中点，∴AD ⊥BC.∴∠ADB ＝90°.∴∠EDF ＝∠EDA ＋∠ADF ＝∠EDA ＋∠BDE ＝∠ADB ＝90°.∴△DEF 为等腰直角三角形．(2)是，理由略．4．证明：如图，过点E 作EF ⊥AC 于F.∵AE ＝EC ，∴AF ＝12AC. 又∵AB ＝12AC ，∴AF ＝AB. ∵AD 平分∠BAC ，∴∠FAE ＝∠BAE.又∵AE ＝AE ，∴△AEF ≌△AEB(SAS )．∴∠ABE ＝∠AFE ＝90°，即EB ⊥AB.(第4题)5．解：如图，延长BA ，CD 交于点E.(第5题)∵BF 平分∠ABC ，CD ⊥BD ，BD ＝BD ，∴△BDC ≌△BDE.∴BC ＝BE.又∵BD ⊥CE ，∴CE ＝2CD.∵∠BAC ＝90°，∠BDC ＝90°，∠AFB ＝∠DFC ，∴∠ABF ＝∠DCF.又∵AB ＝AC ，∠BAF ＝∠CAE ＝90°，∴△ABF ≌△ACE(ASA )．∴BF ＝CE.故BF ＝2CD.6．解：如图，以点A 为圆心，AB 长为半径画弧交CD 于点E ，连接AE ，则AE ＝AB ，所以∠AEB ＝∠ABC.(第6题)又因为AD⊥BC，所以AD是BE边上的中线，即DE＝BD.又因为∠ABC＝2∠C，所以∠AEB＝2∠C.而∠AEB＝180°－∠AEC＝∠CAE＋∠C，所以∠CAE＝∠C.所以CE＝AE＝AB，故CD＝CE ＋DE＝AB＋BD.。

三线合一解题给力◎吴育弟一、推理证明例1 如图1，点D，E在△ABC的BC边上，AB=AC，AD=AE．求证：BD=CE．图1 分析：过点A作BC的垂线，利用等腰三角形的“三线合一”得到P为DE及BC的中点，进而可证．证明：如图1，过点A作AP⊥BC于点P．因为AB=AC，所以BP=PC.因为AD=AE，所以DP=PE.所以BP-DP=PC-PE，即BD=CE.例2如图2，在等边三角形ABC中，D为AC边的中点，E为BC延长线上一点，CE=CD，DM⊥BC于点M.求证：M是BE的中点.分析：连接BD，构造等腰三角形，利用等腰三角形“三线合一”的性质，得出DM是BE边上的中线，从而使问题得证.证明：连接BD.因为△ABC是等边三角形，所以∠ABC=∠ACB=60°，AB=AC=BC.因为C D=CE，所以∠CDE=∠E=1/2∠ACB =30°.因为BD是AC边上的中线，AB=BC，所以BD平分∠ABC，则∠DBC=30°.所以∠DBE=∠E.所以DB=DE.又因为DM⊥BE，所以DM是BE边上的中线，即M是BE的中点．二、判断说理例3 如图3，在△ABC中，AB=AC，AD为BC边上的中线，E为AD边上一点，则∠ABE与∠ACE的大小关系是怎样的？试说明理由图3 分析：根据等腰三角形“三线合一”的性质，可得AD为∠BAC的平分线，所以∠BAD=∠CAD.结合已知条件可判定△ABE≌△ACE，所以∠ABE=∠ACE．解：相等.理由：因为AB=AC，AD为BC边上的中线，所以AD平方∠BAC，所即∠BAE=∠CAE.在△ABE和△ACE中，AB=AC，∠BAE=∠CAE，AE=AE，所以△ABE≌△ACE.所以∠ABE=∠ACE.图2。

三线合一练习题高考数学是每个高中生都必须面对的一道“坎”。

而三线合一题作为数学试卷中的重要部分，也是令很多学生头疼的难题。

在本文中，将给大家介绍三线合一练习题的解题方法和技巧，帮助大家更好地应对这一题型。

在解答三线合一练习题之前，我们先来了解一下三线合一的概念。

三线合一是指将三角形的三条线段合成一条线段。

在三线合一题中，通常给出三角形的三个角度和一个边长，要求计算另外两个边长。

这一题型常常需要用到三角函数的知识，包括正弦定理和余弦定理。

下面以一个具体的例子来说明三线合一练习题的解题过程。

例题：已知三角形ABC，∠A=30°，边AB=8，边AC=6，求边BC 的长度。

解：首先，我们可以利用余弦定理来计算边BC的长度。

余弦定理的公式是：c² = a² + b² - 2ab·cosC根据题目中给出的信息，我们已知边AB和边AC的长度，分别为8和6，∠A的大小为30°，要求的是边BC的长度，设为x。

代入余弦定理的公式，我们可以得到：x² = 8² + 6² - 2·8·6·cos30°接下来，我们需要计算cos30°的值。

根据余弦函数的定义，我们知道cos30°=√3/2。

将cos30°代入上面的公式，我们可以继续计算：x² = 64 + 36 - 96·√3/2x² = 100 - 48√3最后，我们可以求解x的值：x = √(100 - 48√3)这样，我们就得到了边BC的长度。

以上就是解答三线合一练习题的基本步骤和方法。

根据题目给出的已知信息，利用余弦定理或者其他相关的公式，计算出未知边长的值。

除了余弦定理，我们在解答三线合一练习题时还可以利用正弦定理。

正弦定理的公式是：a/sinA = b/sinB = c/sinC当已知三个角度和一个边长时，我们可以利用正弦定理计算其他两个边长的值。

初中数学三线合一解题技巧
三线合一，即在等腰三角形中，底边上的高、底边上的中线、顶角的角平分线，这三线合一。

解题技巧如下：
1. 证明三线合一，首先应明确三角形是否为等腰三角形。

可以通过给定的条件或结论，证明三角形为等腰三角形。

2. 在等腰三角形中，由于两腰相等，对应的两个底角也相等。

因此，可以通过证明两个底角相等，来证明三线合一。

3. 若要证明高也是中线或角平分线，可以通过证明高所在的三角形与原三角形相似或全等，来证明高也是中线或角平分线。

4. 在证明过程中，要注意使用给定的条件和结论，以及相关的定理和性质。

下面是一个具体的例子：
题目：在$\bigtriangleup ABC$中，$AB = AC$，$\angle BAC =
120^{\circ}$，$D$是$BC$上一点，$BD = AD$，求证：$CD = 2BD$。

证明：
1. 由于$AB = AC$，根据等腰三角形的性质，$\angle B = \angle C$。

2. 又因为$\angle BAC = 120^{\circ}$，所以$\angle B = \angle C = 30^{\circ}$。

3. 在$\bigtriangleup ABD$中，由于$\angle ABD = 30^{\circ}$，根据三角形的性质，有$BD = \frac{1}{2}AD$。

4. 又因为$BD = AD$，所以$AD = BD = CD$。

5. 因此，$CD = 2BD$。

等腰三角形性质：三线合一”好解题教学目标：1.知识与技能目标：掌握等腰三角形三线合一的性质。

2.过程与方法目标：通过对性质的复习和例题的分析，培养学生多角度思考问题的习惯，提高学生分析问题和解决问题的能力。

3.情感与态度目标：体验数学活动充满着探索性和创造性，在小组合作活动中，培养学生之间的合作精神。

教学重点：等腰三角形“三线合一”的重要性质应用。

教学难点：等腰三角形“三线合一”性质应用于证明两线垂直、两线段相等和两角相等。

一、知识点回顾等腰三角形性质：（1）等腰三角形是轴对称图形（2）等腰三角形顶角、底边上的、底边上的互相重合。

等腰三角形“三线合一”性质。

几何语言：∵AB=AC,AD⊥BC∴BD=CD，或∠BAD=∠CAD（三线合一）（3）等腰三角形两底角相等几何语言：∵AB=AC ∴∠B=∠C（等边对等角）二、例题讲解类型一：求线段的长例1：如图，在△ABC中，AB＝AC，AD＝DB＝BC，DE⊥AB于点E，若CD＝4，且△BDC的周长为24，求AE的长．类型二：说明角相等例2：如图，在△ABC中，AB＝AC，AD是BC 边上的中线，BE⊥AC于点E．求证：∠CBE＝∠BAD．练习：如图，在等腰△ABC中，CH是底边上的高线，点P是线段CH上不与端点重合的任意一点，连接AP 交BC于点E，连接BP交AC于点F．证明：∠CAE＝∠CBF类型三：说明两线垂直例3：如图，在△ABC中，D是AB上一点，且BD=BC，CE=DE.证明：CD ⊥BE练习：如图，已知AB=AE,∠ABC=∠AED,BC=ED，F是CD的中点，AF与CD有什么位置关系？请说明理由三、小结：“三线合一”性质可用来证明（1）求线段的长（2）两角相等（3）两线垂直四、反思：等腰三角形在初中几何里很基础也很常见，其中等腰三角形的性质在实际的应用中非常普遍，尤其是“三线合一”这一重要定理.在初中几何证明和计算中占据了非常重要的地位，学生既需要知道它的由来，还要知道它的用途，还应在图形不全的情况下补全三线合一所在的基本图形，老师如果把握好等腰三角形“三线合一”性质在教学中的应用，把握好化归思想方法的渗透，将有助于让学生把握解题的关键，更好地培养和发展学生的思维能力，有助于学生突破解题的难点，探明解题的方法，从而帮助学生提高解决问题的能力。