高级微观经济学 (黄有光) AdMicro-L1-MathTools

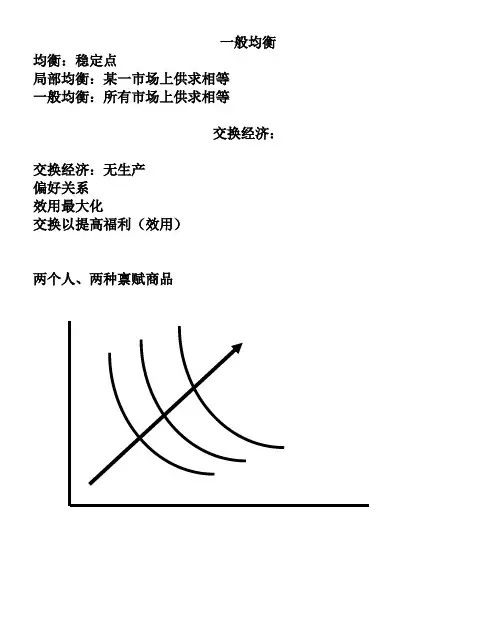
一般均衡均衡：稳定点局部均衡：某一市场上供求相等一般均衡：所有市场上供求相等交换经济：交换经济：无生产偏好关系效用最大化交换以提高福利（效用）两个人、两种禀赋商品Edgeworth 图 禀赋点为e假设自主交换能够实现帕累托改进，达到更优的配置点x对消费者1，其所偏好e 的区域为红色区域，最终的配置点必须在这一区域内，否那么，他拒绝交换或抵制这一配置。

对消费者2，其所偏好e 的区域为蓝色区域，最终的配置点必须在这一区域内，否那么，他拒绝交换或抵制这一配置。

因此，最终的配置点必须在重叠的区域中——凸透镜区域内和边上。

在这一区域里，双方或至少一方的福利能够提高。

11ee设交换后形成的配置点'x 在凸透镜内部，双方福利都得到改善，同时各有一条无差异曲线交于此点。

双方进一步通过交换改善彼此福利。

对消费者1，其所偏好'x 的区域为红色区域，最终的配置点必须在这一区域内，否那么，他拒绝交换或抵制这一配置。

对消费者2，其所偏好'x 的区域为蓝色区域，最终的配置点必须在这一区域内，否那么，他拒绝交换或抵制这一配置。

因此，最终的配置点必须在重叠的区域中——凸透镜区域内和边上。

在这一区域里，双方或至少一方的福利能够提高。

11ee'x交换过程持续下去，凸透镜越来越小，最终变为一个点：两条无差异曲线的切点：x 。

此时，双方进一步交换会使某一方福利下降。

所以，双方的交换一旦达到了切点位置，就不会有交换发生。

实现了帕累托最优。

在凸透镜内部和边上，这样的点有无数多个，最终的配置究竟是哪一个点，我们并不知道，或者说，我们不知道决定最终的帕累托效率点的位置的因素是什么。

结论只是：帕累托效率点位于凸透镜边上或内部的某个切点位置上。

11eexEdgeworth图中，所有的无差异曲线的切点的连线构成契约线，帕累托效率点是凸透镜与契约线交集中的点。

2 11eex当禀赋点落在契约线上时，即为帕累托效率点，无交换发生。

高级微观经济学
高级微观经济学（Advanced Microeconomics）是经济学中的一个分支，它深入研究个体经济主体和市场之间的相互关系。

与基础微观经济学相比，高级微观经济学更加理论性和复杂，涉及更深层次的经济学原理和模型。

高级微观经济学的研究内容包括：
1. 个体消费者和生产者的行为：研究消费者如何做出消费决策，生产者如何决定生产规模和价格。

2. 市场结构和竞争：研究市场的竞争程度和不完全竞争条件下的市场行为，如寡头垄断、垄断和寡头竞争。

3. 市场失灵：研究市场存在的各种制度和机制不完善导致的市场失灵现象，如外部性、公共物品和信息不对称等问题。

4. 游戏论和博弈论：研究个体之间的战略互动和决策过程，探讨不同策略下可能的结果。

5. 经济激励和合同理论：研究如何通过激励机制和合同设
计来引导经济主体的行为，如契约理论和机制设计等。

6. 不完全信息和不确定性：研究在信息有限和不确定性条
件下个体的决策行为和市场运行情况。

高级微观经济学的研究方法强调理论建模和分析，常常使
用数学和形式化的方法来描述经济行为和市场机制。

它是
经济学家、政策制定者和企业家等经济管理者理解经济现
象和制定决策的重要工具。

2.Properties of PS.
• Additive (free entrance) :
y Y,and y Y, then y y Y • Convexity: y Y,and y Y, then y (1 )y Y, here [0,1]
See the fig.
• Proposition1: if Y is convex, so is V(q). • Proposition2: if V(q) is convex, f(x) is quasiconcave.
lecture 1 for Chu Kechen Honors College
y Y, ay Y, a 0
lecture 1 for Chu Kechen Honors College
4.Returns to scale
• Proposition 3: Y is constant returns to
scale if Y is both “additive” and “convexity”. • Proposition 4: single production, if and only if f(.) is homogenous of degree 1, Y is constant returns to scale.
the array y y, and y Y means y Y • No free lunch: Y n {0}
n n
See the fig.
• Free disposal:
See the fig.
lecture 1
y n Y
for Chu Kechen Honors College

Advanced Microeconomics Topic 3: Consumer DemandPrimary Readings: DL – Chapter 5; JR - Chapter 3; Varian, Chapters 7-9.3.1 Marshallian Demand FunctionsLet X be the consumer's consumption set and assume that the X = R m +. For a given price vector p of commodities and the level of income y , the consumer tries to solve the following problem:max u (x )subject to p ⋅x = y x ∈ X• The function x (p , y ) that solves the above problem is called the consumer's demand function .• It is also referred as the Marshallian demand function . Other commonly known namesinclude Walrasian demand correspondence/function , ordinary demand functions , market demand functions , and money income demands .• The binding property of the budget constraint at the optimal solution, i.e., p ⋅x = y , is theWalras’ Law .• It is easy to see that x (p , y ) is homogeneous of degree 0 in p and y .Examples:(1) Cobb-Douglas Utility Function:.,...,1,0 ,)(1m i x x u i mi i i =>=∏=ααFrom the example in the last lecture, the Marshallian demand functions are:.ii i p yx αα=where∑==mi i 1αα.(2) CES Utility Functions: )10( )(),(/12121<≠+=ρρρρx x x x uThen the Marshallian demands are:,),( ;),(2112221111rr r r r r p p yp y x p p y p y x +=+=--p p where r = ρ/(ρ -1). And the corresponding indirect utility function is given byrr r p p y y v /121)(),(-+=pLet us derive these results. Note that the indirect utility function is the result of the utility maximization problem:yx p x p x x x x =++2211/121, subject to )(max 21ρρρDefine the Lagrangian function:)()(),,(2211/12121y x p x p x x x x L -+-+=λλρρρThe FOCs are:00)(0)(22112121)/1(2121111)/1(211=-+=∂∂=-+=∂∂=-+=∂∂----y x p x p Lp x x x x L p x x x x L λλλρρρρρρρρ Eliminating λ, we get⎪⎩⎪⎨⎧+=⎪⎪⎭⎫⎝⎛=-2211)1/(12121x p x p y p p x x ρ So the Marshallian demand functions are:rr r rrr p p yp y x x p p yp y x x 211222211111),(),(+==+==--p pwith r = ρ/(ρ-1). So the corresponding indirect utility function is given by:r r r p p y y x y x u y v /12121)()),(),,((),(-+==p p p3.2 Optimality Conditions for Co nsumer’s ProblemFirst-Order ConditionsThe Lagrangian for the utility maximization problem can be written asL = u (x ) - λ( p ⋅x - y ).Then the first-order conditions for an interior solution are:yu i p x u i i =⋅=∇∀=∂∂x p p x x λλ)( i.e. ;)( (1)Rewriting the first set of conditions in (1) leads to,,k j p p MU MU MRS kj kj kj ≠==which is a direct generalization of the tangency condition for two-commodity case.Sufficiency of First-Order ConditionsProposition : Suppose that u (x ) is continuous and quasiconcave on R m +, and that (p , y ) > 0. If u if differentiable at x*, and (x*, λ*) > 0 solves (1), then x* solve the consumer's utility maximization problem at prices p and income y .Proof . We will use the following fact without a proof:• For all x , x ' ≥ 0 such that u (x') ≥ u (x ), if u is quasiconcave and differentiable at x , then∇u (x )(x' - x ) ≥ 0.Now suppose that ∇u (x*) exists and (x*, λ*) > 0 solves (1). Then,∇u (x*) = λ*p , p ⋅x* = y .If x* is not utility-maximizing, then must exist some x 0 ≥ 0 such thatu (x 0) > u (x*) and p ⋅x 0 ≤ y .Since u is continuous and y > 0, the above inequalities implies thatu (t x 0) > u (x*) and p ⋅(t x 0) < yfor some t ∈ [0, 1] close enough to one. Letting x' = t x 0, we then have∇u (x*)(x' - x ) = (λ*p )⋅( x' - x ) = λ*( p ⋅x' - p ⋅x ) < λ*(y - y ) = 0,which contradicts to the fact presented at the beginning of the proof since u (x 1) > u (x*).Remark• Note that the requirement that (x*, λ*) > 0 means that the result is true only forinterior solutions.Roy's IdentityNote that the indirect utility function is defined as the "value function" of the utility maximization problem. Therefore, we can use the Envelope Theorem to quickly derive the famous Roy's identity.Proposition (Roy's Identity?): If the indirect utility function v (p , y ) is differentiable at (p 0, y 0) and assume that ∂v (p 0, y 0)/ ∂y ≠ 0, then.,...,1 ,),(),(),(000000m i yy v p y v y x ii =∂∂∂∂-=p p pProof . Let x * = x (p , y ) and λ* be the optimal solution associated with the Lagrangian function:L = u (x ) - λ( p ⋅x - y ).First applying the Envelope Theorem, to evaluate ∂v (p 0, y 0)/ ∂p i gives.**)*,(),(*i ii x p L p y v λλ-=∂∂=∂∂x p But it is clear that λ* = ∂v (p , y )/ ∂y , which immediately leads to the Roy's identity.Exercise• Verify the Roy's identity for CES utility function.Inverse Demand FunctionsSometimes, it is convenient to express price vector in terms of the quantity demanded, which leads to the so-called inverse demand functions .• the inverse demand function may not always exist. But the following conditions willguarantee the existence of p (x ):• u is continuous, strictly monotonic and strictly quasiconcave. (In fact, these conditionswill imply that the Marshallian demand functions are uniquely defined.)Exercise (Duality of Indirect and Direct Demand Functions):(1) Show that for y = 1 the inverse demand function p = p (x ) is given by:.,...,1 ,)()()(1m i x x u x u p m j j jii =∂∂∂∂=∑=x x x(Consult JR, pp.79-80.)(2) Show that for y = 1, the (direct) demand function x = x (p, 1) satisfies.,...,1 ,)1,()1,()1,(1m i p p v p v x m j j j ii =∂∂∂∂=∑=p p p(Hint: Use Roy’s identity and the homogeneity of degree zero of the indirect uti lityfunction.)3.3 Hicksian Demand FunctionsRecall that the expenditure function e (p , u ) is the minimum-value function of the following optimization problem:,)( s.t. min ),(u u u e m≥⋅=+∈x x p p R x for all p > 0 and all attainable utility levels.It is clear that e (p , u ) is well-defined because for p ∈ R m ++, x ∈ R m +, p ⋅x ≥ 0.If the utility function u is continuous and strictly quasiconcave, then the solution to the above problem is unique, so we can denote the solution as the function x h (p , u ) ≥ 0. By definition, it follows thate (p , u ) = p ⋅x h (p , u ).• x h (p , u ) is called the compensated demand functions , also commonly known as Hicksiandemand functions , named after John Hicks when he first discussed this type of demand functions in 1939.Remarks1. The reason that they are called "compensated " demand function is that we mustimpose an artificial income adjustment when the price of one good is changing while the utility level is assumed to be fixed.2. It is important to understand that, in contrast with the Marshallian demands, theHicksian demands are not directly observable.As usual, it should be no longer a surprise that there is a close link between the expenditure function and the Hicksian demands, as summarized in the following result, which is again a direct application of the Envelope Theorem..Proposition (Shephard's Lemma for Consumer): If e (p , u ) is differentiable in p at (p 0, u 0) with p 0 > 0, then,.,...,1 ,),(),(000m i p u e u x ih i=∂∂=p pExample: CES Utility Functions)10( )(),(/12121<≠+=ρρρρx x x x uLet us now derive the Hicksian demands and the corresponding expenditure function.min {p 1x 1 + p 2x 2} subject to)(/121u x x =+ρρρThe Lagrangian function is))((),,(/121221121u x x x p x p x x L -+-+=ρρρλλThen the FOCs are:0)(0)((0)((/121121/12122111/12111=+-=∂∂=+-=∂∂=+-=∂∂----ρρρρρρρρρρρλλλx x u L x x x p x L x x x p x L Eliminating λ, we getρρρρ/121)1/(12121)(x x u p p x x +=⎪⎪⎭⎫ ⎝⎛=- From these, it is easy to derive the Hicksian demand functions given by:121)/1(212111)/1(211)(),()(),(----+=+=r r r r h r r r r h pp p u u x p p p u u x p pwhere r = ρ/(ρ-1). And the expenditure function is.)(),(),(),(/1212211rr r h h p p u u x p u x p u e +=+=p p pAlternatively, since we know that the indirect utility function is given by:,)(),(/121rr r p p y y v -+=p3.4 Recall that (last the indirect utility function v (p (a) e (p , v (b) v (p , eFurthermore, we solutions ofboth optimization the following interesting identities between Marshallian demands and Hicksian demands:x (p , y ) = x h (p , v (p , y )) x h (p , u ) = x (p , e (p , u ))which hold for all values of p , y and u .The second identity leads to a classic differentiation relation between Hicksian demands and Marshallian demands, known as Slutsky equation.Proposition (Slutsky Equation): If the Marshallian and Hicksian demands are all well-defined and continuously differentiable, then for p > 0, x > 0,),,(),(),(),(y x yy x p u x p y x j i j h i j i p p p p ⋅∂∂-∂∂=∂∂where u = v (p , y ).Proof . It follows easily from taking derivative and applying Shephard's Lemma.Substitution and Income Effects• The significance of Slutsky equation is that it decomposes the change caused by a pricechange into two effects: a substitution effect and an income effect .• The substitution effect is the change in compensated demand due to the change inrelative prices, which is the first item in Slutsky equation.• The income effect is the change in demand due to the effective change in incomecaused by the price change, which is the second item in Slutsky equation. • The substitution effect is unobservable, while the income effect is observable.Question: From the above diagram (also know as Hicksian decomposition ), can you see crossing property between a Marshallian demand function and the corresponding Hicksian demand? (Hint: there are two general cases.)Slutsky MatrixThe substitution effect between good i and good j is measured byj i p u x s jh i ij ,,),(∀∂∂=pSo the Slutsky matrix or the substitution matrix is the m ⨯m matrix of the substitution items:⎥⎥⎦⎤⎢⎢⎣⎡∂∂==j h i ij p u x s ),(][p SThe following result summarizes the basic properties of the Slutsky matrix.Proposition (Substitution Properties). The Slutsky matrix S is symmetric and negative semidefinite.Proof . By Shephard’s Lemma (for consumer), we know thatji ihj i j j i j h i ij s p u x p p u e p p u e p u x s =∂∂=∂∂∂=∂∂∂=∂∂=),(),(),(),(22p p p pHence S is symmetric. It is evident that S is the Hessian matrix of the expenditure function e (p , u ).Since we know that e (p , u ) is concave, so its Hessian matrix must be negative semidefinite.Since the second-order own partial derivatives of a concave function are always nonpositive, this implies that s ii ≤ 0, i.e.,i p u x s ih i ii ∀≤∂∂=,0),(pwhich indicates the intuitive property of a demand function: as its own price increases, the quantity demanded will decrease. You are reminded that this is a general property for Hicksian demands.For the Marshallian demands, note that by Slutsky equation,).,(),(),(),(y x yy x p u x p y x i i i h i i i p p p p ⋅∂∂-∂∂=∂∂Then for a small change in p i , we will have the following:.),(),(),(),(i i i i i h i i i i i p y x yy x p p u x p p y x x ∆⋅∂∂-∆∂∂=∆∂∂≈∆p p p pThe first item, capturing the own price effect of the Hicksian demands, is of course nonpositive.The sign of the second item depends on the nature of the good:• Normal good : ∂x i (p , y )/ ∂y > 0.• This leads to a normal Marshallian demand function: it is decreasing in its ownprice.• Inferior good : ∂x i (p , y )/ ∂y < 0.• When the substitution effect still dominates the income effect, the resultingMarshallian demand is also decreasing in its own price.• When the substitution effect is dominated by the income effect, it will lead to aGiffen good, that is, its demand function is an increasing function of its own price.Because of Slutsky equation, the Slutsky matrix (i.e., the substitution matrix) also has the following form that is in terms of Marshallian demand functions.⎥⎥⎦⎤⎢⎢⎣⎡∂∂+∂∂=⎥⎥⎦⎤⎢⎢⎣⎡∂∂==),(),(),(),(][y x y y x p y x p u x s j i j i j h i ij p p p p SWe will get back to the above Slutsky matrix in the next lecture when we discuss the integrability problem .3.5. The Elasticity Relations for Marshallian Demand FunctionsDefinition . Let x (p , y ) be the consumer’s Marshallian demand functions. Define.),(,),(),(,),(),(yy x p s y x p p y x y x yy y x i i i i jj i ij i i i p p p p p =∂∂=∂∂=εηThen1. ηi is called the income elasticity of demand for good i .2. ε ij is called the price elasticity of the demand for good i with respect to a price change ingood j . ε ii is the own-price elasticity of the demand for good i . For i ≠ j , ε ij is the cross-price elasticity .3. s i is called the income share spent on good i .The following result summarizes some important relationships among the income shares, income elasticities and the price elasticities.Proposition . Let x (p , y ) be the consumer’s Marshallian demand functions. Then1. Engel aggregation :.11=∑=mi ii s η2. Cournot aggregation :.,...,1 ,1m j s s j mi iji =-=∑=εProof . Both identities are derived from the Walras’ Law, namely, the fact that the budget is tight or balanced:y = p ⋅x (p , y ) for all p and y . (A)To prove Engel aggregation, we differentiate both sides of (A) w.r.t. y :∑∑∑====∂∂=∂∂=m i mi i i ii i i mi i i s y x yy y x y y x p y y x p 111,),(),(),(),(1ηp p p pas required.To prove Cournot aggregation, we differentiate both sides of (A) w.r.t. p j :.),(),(),(),(),(01∑∑=≠∂∂=-⇒∂∂++∂∂=mi j i i j jj jj ji j i ip y x p y x p y x p y x p y x p p p p p pMultiplying both sides by p j /y leads to∑∑∑====-⇒∂∂=∂∂=-mi iji j mi i jj i i i mi j j i i j j s s y x p p y x y y x p p p y x y p yy x p 111),(),(),(),(),(εp p p p pas required too.3.6 Hicks ’ Composite Commodity TheoremAny group of goods & services with no change in relative prices between themselves may be treated as a single composite commodity, with the price of any one of the group used as the price of the composite good and the quantity of the composite good defined as the aggregate value of the whole group divided by this price. Important use in applied economic analysis.Additional ReferencesAfriat, S. (1967) "The Construction of Utility Functions from Expenditure Data," International Economic Review, 8, 67-77.Arrow, K. J. (1951, 1963) Social Choice and Individual Values. 1st Ed., Yale University Press, New Haven, 1951; 2nd Ed., John Wiley & Sons, New York, 1963.Becker, G. S. (1962) "Irrational Behavior and Economic Theory," Journal of Political Economy, 70, 1-13.Cook, P. (1972) "A One-line Proof of the Slutsky Equation," American Economic Review, 42, 139. Deaton, A. and J. Muellbauer (1980) Economics and Consumer Behavior. Cambridge University Press, Cambridge.Debreu, G. (1959) Theory of Value. John Wiley & Sons, New York.Debreu, G. (1960) "Topological Methods in Cardinal Utility Theory," in Mathematical Methods in the Social Sciences, ed. K. J. Arrow and M. D. Intriligator, North Holland, Amsterdam. Diewert, W. E. (1982) "Duality Approaches to Microeconomic Theory," Chapter 12 in Handbook of Mathematical Economics, ed. K. J. Arrow and M. D. Intriligator, North Holland, Amsterdam.Gorman, T. (1953) “Community Preference Fields,” Econometrica, 21, 63-80.Hicks, J. (1946) V alue and Capital. Clarendon Press, Oxford, England.Katzner, D.W. (1970) Static Demand Theory. MacMillan, New York.Marshall, A. (1920) Principle of Economics, 8th Ed. MacMillan, London.McKenzie, L. (1957) “Demand Theory Without a Utility In dex," Review of Economic Studies, 24, 183-189.Pollak, R. (1969) "Conditional Demand Functions and Consumption Theory," Quarterly Journal of Economics, 83, 60-78.Roy, R. (1942) De l'utilite. Hermann, Paris.Roy, R. (1947) "La distribution de revenu entre les divers biens," Econometrica, 15, 205-225. Samuelson, P. A. (1938) "A Note on the Pure Theory of Consumer's Behavior," Econometrica, 5, 61-71, 353-354.Samuelson, P. (1947) Foundations of Economic Analysis. Harvard University Press, Cambridge, Massachusetts.Sen, (1970) Collective Choice and Social Welfare. Holden Day, San Francisco.Stigler, G. (1950) "Development of Utility Theory," Journal of Political Economy, 59, parts 1 & 2, pp. 307-327, 373-396.Varian, H. R. (1992) Microeconomic Analysis. Third Edition. W.W. Norton & Company, New York. (Chapters 7, 8 and 9)Wold, H. and L. Jureen (1953) Demand Analysis. John Wiley & Sons, New York.11。

《高级微观经济学》课程教学大纲一、课程名称（宋小四号粗体，以下标题同）1．中文名称：高级微观经济学2．英文名称：Advanced Microeconomic Theory二、课程概况课程类别：学位必修课学时数：32学分数：2适用专业：交通运输学院开课学期：1开课单位：经济管理学院三、四、教学目的及要求培养学员以严谨方式分析经济理论问题的能力，培养学员的经济学思维方式，掌握微观经济学的前沿理论和现代方法体系，为今后深入研究经济学铺垫基石。

通过本课程教学，希望加深读者对经济学理论精髓的理解，把读者引向当代经济学研究的前沿，并能灵活运用经济学原理深入、系统地分析现实经济问题。

本课程采用启发式教学，注重进一步提高学员发现、分析和解决经济理论问题的能力。

五、课程主要内容及先修课程主要内容：(1) 从对经济学的深层含义分析入手，反思经济学基本问题，回顾发展历程，分析研究动态，阐明微观经济学的发展趋势。

（5学时）(2) 通过对经济活动主体、市场结构、经济行为与商品空间的深入剖析，实现高级与中级微观经济学之间的有效衔接。

尤其是建立一般商品空间理论，以反映20世纪90年代以来经济学研究的新动向。

（5学时）(3) 建立消费选择的完整理论体系，特别是要建立确定性条件下的效用公理体系，揭示消费者需求的逻辑事实。

（5学时）(4) 以个人需求为基础来建立总需求理论，为宏观经济分析奠定微观基础。

（5学时）(5) 全面论述不确定条件下的个人选择问题，建立完整的理论体系，包括预期效用理论、主观概率理论、风险规避度量理论、资产需求理论。

（5学时）(6) 建立完整的生产者行为理论，包括单一产品的生产理论和多种产品的生产理论。

（5学时）(7) 运用博弈论方法严格论述一般均衡与社会福利问题，建立令人满意的一般经济均衡理论体系。

（5学时）先修课程：中级微观经济学、中级宏观经济学、货币银行学、公共财政学、数学分析、高等代数、实变函数、概率论、泛函分析初步知识六、课程教学方法32小时的课堂教学七、课程考核方式考试八、课程使用教材杰弗瑞的《高级微观经济学》九、课程主要参考资料1．A. Mas-Colell, M. D. Whinston & J. R. Green, Microeconomic Theory, Oford University Press, 19952．K. J. Arrow & M. D. Intriligator, Handbook of Mathematical Economics, VolumeI, Elsevier Science Publishers, 19813. K. J. Arrow & M. D. Intriligator, Handbook of Mathematical Economics, Volume II, Elsevier Science Publishers, 19824. K. J. Arrow & M. D. Intriligator, Handbook of Mathematical Economics, Volume III, Elsevier Science Publishers, 1986分委员会主席审批：年月日学院主管院长审批：年月日编号：C3/研部03/002注：（1）英文课程名称务必写准确；（2）需编写的内容统一用宋小四号，行间距固定值22磅。

825微观经济学参考书目-回复微观经济学参考书目如下：1. "微观经济学原理" （Principles of Microeconomics）- Mankiw, N. Gregory2. "微观经济学" （Microeconomics）- Perloff, Jeffrey M.3. "微观经济学导论" （Microeconomics: An Intuitive Approach with Calculus）- Nechyba, Thomas J.4. "微观经济学" （Microeconomic Theory）- Mas-Colell, Andreu, Whinston, Michael D., and Green, Jerry R.5. "高级微观经济学" （Advanced Microeconomic Theory）- Jehle, Geoffrey A. and Reny, Philip J.6. "微观经济学分析" （Intermediate Microeconomics and Its Application）- Nicholson, Walter and Snyder, Christopher M.7. "微观经济学" （Microeconomics for Managers）- Kreps, David M.这些参考书目覆盖了微观经济学的基本概念、理论和应用。

下面，我将逐步回答这一主题，并简要介绍每本参考书目的内容和特点。

首先，我们来看"Mankiw, N. Gregory"的"微观经济学原理"。

这本书是学习微观经济学的经典教材之一，它介绍了微观经济学的基本原理和概念，包括供求关系、市场均衡、消费者行为、生产者行为等。

Advanced Microeconomics Topic 3: Consumer DemandPrimary Readings: DL – Chapter 5; JR - Chapter 3; Varian, Chapters 7-9.3.1 Marshallian Demand FunctionsLet X be the consumer's consumption set and assume that the X = R m +. For a given price vector p of commodities and the level of income y , the consumer tries to solve the following problem:max u (x )subject to p ⋅x = y x ∈ X• The function x (p , y ) that solves the above problem is called the consumer's demand function .• It is also referred as the Marshallian demand function . Other commonly known namesinclude Walrasian demand correspondence/function , ordinary demand functions , market demand functions , and money income demands .• The binding property of the budget constraint at the optimal solution, i.e., p ⋅x = y , is theWalras’ Law .• It is easy to see that x (p , y ) is homogeneous of degree 0 in p and y .Examples:(1) Cobb-Douglas Utility Function:.,...,1,0 ,)(1m i x x u i mi i i =>=∏=ααFrom the example in the last lecture, the Marshallian demand functions are:.ii i p yx αα=where∑==mi i 1αα.(2) CES Utility Functions: )10( )(),(/12121<≠+=ρρρρx x x x uThen the Marshallian demands are:,),( ;),(2112221111rr r r r r p p yp y x p p y p y x +=+=--p p where r = ρ/(ρ -1). And the corresponding indirect utility function is given byrr r p p y y v /121)(),(-+=pLet us derive these results. Note that the indirect utility function is the result of the utility maximization problem:yx p x p x x x x =++2211/121, subject to )(max 21ρρρDefine the Lagrangian function:)()(),,(2211/12121y x p x p x x x x L -+-+=λλρρρThe FOCs are:00)(0)(22112121)/1(2121111)/1(211=-+=∂∂=-+=∂∂=-+=∂∂----y x p x p Lp x x x x L p x x x x L λλλρρρρρρρρ Eliminating λ, we get⎪⎩⎪⎨⎧+=⎪⎪⎭⎫⎝⎛=-2211)1/(12121x p x p y p p x x ρ So the Marshallian demand functions are:rr r rrr p p yp y x x p p yp y x x 211222211111),(),(+==+==--p pwith r = ρ/(ρ-1). So the corresponding indirect utility function is given by:r r r p p y y x y x u y v /12121)()),(),,((),(-+==p p p3.2 Optimality Conditions for Co nsumer’s ProblemFirst-Order ConditionsThe Lagrangian for the utility maximization problem can be written asL = u (x ) - λ( p ⋅x - y ).Then the first-order conditions for an interior solution are:yu i p x u i i =⋅=∇∀=∂∂x p p x x λλ)( i.e. ;)( (1)Rewriting the first set of conditions in (1) leads to,,k j p p MU MU MRS kj kj kj ≠==which is a direct generalization of the tangency condition for two-commodity case.Sufficiency of First-Order ConditionsProposition : Suppose that u (x ) is continuous and quasiconcave on R m +, and that (p , y ) > 0. If u if differentiable at x*, and (x*, λ*) > 0 solves (1), then x* solve the consumer's utility maximization problem at prices p and income y .Proof . We will use the following fact without a proof:• For all x , x ' ≥ 0 such that u (x') ≥ u (x ), if u is quasiconcave and differentiable at x , then∇u (x )(x' - x ) ≥ 0.Now suppose that ∇u (x*) exists and (x*, λ*) > 0 solves (1). Then,∇u (x*) = λ*p , p ⋅x* = y .If x* is not utility-maximizing, then must exist some x 0 ≥ 0 such thatu (x 0) > u (x*) and p ⋅x 0 ≤ y .Since u is continuous and y > 0, the above inequalities implies thatu (t x 0) > u (x*) and p ⋅(t x 0) < yfor some t ∈ [0, 1] close enough to one. Letting x' = t x 0, we then have∇u (x*)(x' - x ) = (λ*p )⋅( x' - x ) = λ*( p ⋅x' - p ⋅x ) < λ*(y - y ) = 0,which contradicts to the fact presented at the beginning of the proof since u (x 1) > u (x*).Remark• Note that the requirement that (x*, λ*) > 0 means that the result is true only forinterior solutions.Roy's IdentityNote that the indirect utility function is defined as the "value function" of the utility maximization problem. Therefore, we can use the Envelope Theorem to quickly derive the famous Roy's identity.Proposition (Roy's Identity?): If the indirect utility function v (p , y ) is differentiable at (p 0, y 0) and assume that ∂v (p 0, y 0)/ ∂y ≠ 0, then.,...,1 ,),(),(),(000000m i yy v p y v y x ii =∂∂∂∂-=p p pProof . Let x * = x (p , y ) and λ* be the optimal solution associated with the Lagrangian function:L = u (x ) - λ( p ⋅x - y ).First applying the Envelope Theorem, to evaluate ∂v (p 0, y 0)/ ∂p i gives.**)*,(),(*i ii x p L p y v λλ-=∂∂=∂∂x p But it is clear that λ* = ∂v (p , y )/ ∂y , which immediately leads to the Roy's identity.Exercise• Verify the Roy's identity for CES utility function.Inverse Demand FunctionsSometimes, it is convenient to express price vector in terms of the quantity demanded, which leads to the so-called inverse demand functions .• the inverse demand function may not always exist. But the following conditions willguarantee the existence of p (x ):• u is continuous, strictly monotonic and strictly quasiconcave. (In fact, these conditionswill imply that the Marshallian demand functions are uniquely defined.)Exercise (Duality of Indirect and Direct Demand Functions):(1) Show that for y = 1 the inverse demand function p = p (x ) is given by:.,...,1 ,)()()(1m i x x u x u p m j j jii =∂∂∂∂=∑=x x x(Consult JR, pp.79-80.)(2) Show that for y = 1, the (direct) demand function x = x (p, 1) satisfies.,...,1 ,)1,()1,()1,(1m i p p v p v x m j j j ii =∂∂∂∂=∑=p p p(Hint: Use Roy’s identity and the homogeneity of degree zero of the indirect uti lityfunction.)3.3 Hicksian Demand FunctionsRecall that the expenditure function e (p , u ) is the minimum-value function of the following optimization problem:,)( s.t. min ),(u u u e m≥⋅=+∈x x p p R x for all p > 0 and all attainable utility levels.It is clear that e (p , u ) is well-defined because for p ∈ R m ++, x ∈ R m +, p ⋅x ≥ 0.If the utility function u is continuous and strictly quasiconcave, then the solution to the above problem is unique, so we can denote the solution as the function x h (p , u ) ≥ 0. By definition, it follows thate (p , u ) = p ⋅x h (p , u ).• x h (p , u ) is called the compensated demand functions , also commonly known as Hicksiandemand functions , named after John Hicks when he first discussed this type of demand functions in 1939.Remarks1. The reason that they are called "compensated " demand function is that we mustimpose an artificial income adjustment when the price of one good is changing while the utility level is assumed to be fixed.2. It is important to understand that, in contrast with the Marshallian demands, theHicksian demands are not directly observable.As usual, it should be no longer a surprise that there is a close link between the expenditure function and the Hicksian demands, as summarized in the following result, which is again a direct application of the Envelope Theorem..Proposition (Shephard's Lemma for Consumer): If e (p , u ) is differentiable in p at (p 0, u 0) with p 0 > 0, then,.,...,1 ,),(),(000m i p u e u x ih i=∂∂=p pExample: CES Utility Functions)10( )(),(/12121<≠+=ρρρρx x x x uLet us now derive the Hicksian demands and the corresponding expenditure function.min {p 1x 1 + p 2x 2} subject to)(/121u x x =+ρρρThe Lagrangian function is))((),,(/121221121u x x x p x p x x L -+-+=ρρρλλThen the FOCs are:0)(0)((0)((/121121/12122111/12111=+-=∂∂=+-=∂∂=+-=∂∂----ρρρρρρρρρρρλλλx x u L x x x p x L x x x p x L Eliminating λ, we getρρρρ/121)1/(12121)(x x u p p x x +=⎪⎪⎭⎫ ⎝⎛=- From these, it is easy to derive the Hicksian demand functions given by:121)/1(212111)/1(211)(),()(),(----+=+=r r r r h r r r r h pp p u u x p p p u u x p pwhere r = ρ/(ρ-1). And the expenditure function is.)(),(),(),(/1212211rr r h h p p u u x p u x p u e +=+=p p pAlternatively, since we know that the indirect utility function is given by:,)(),(/121rr r p p y y v -+=p3.4 Recall that (last the indirect utility function v (p (a) e (p , v (b) v (p , eFurthermore, we solutions ofboth optimization the following interesting identities between Marshallian demands and Hicksian demands:x (p , y ) = x h (p , v (p , y )) x h (p , u ) = x (p , e (p , u ))which hold for all values of p , y and u .The second identity leads to a classic differentiation relation between Hicksian demands and Marshallian demands, known as Slutsky equation.Proposition (Slutsky Equation): If the Marshallian and Hicksian demands are all well-defined and continuously differentiable, then for p > 0, x > 0,),,(),(),(),(y x yy x p u x p y x j i j h i j i p p p p ⋅∂∂-∂∂=∂∂where u = v (p , y ).Proof . It follows easily from taking derivative and applying Shephard's Lemma.Substitution and Income Effects• The significance of Slutsky equation is that it decomposes the change caused by a pricechange into two effects: a substitution effect and an income effect .• The substitution effect is the change in compensated demand due to the change inrelative prices, which is the first item in Slutsky equation.• The income effect is the change in demand due to the effective change in incomecaused by the price change, which is the second item in Slutsky equation. • The substitution effect is unobservable, while the income effect is observable.Question: From the above diagram (also know as Hicksian decomposition ), can you see crossing property between a Marshallian demand function and the corresponding Hicksian demand? (Hint: there are two general cases.)Slutsky MatrixThe substitution effect between good i and good j is measured byj i p u x s jh i ij ,,),(∀∂∂=pSo the Slutsky matrix or the substitution matrix is the m ⨯m matrix of the substitution items:⎥⎥⎦⎤⎢⎢⎣⎡∂∂==j h i ij p u x s ),(][p SThe following result summarizes the basic properties of the Slutsky matrix.Proposition (Substitution Properties). The Slutsky matrix S is symmetric and negative semidefinite.Proof . By Shephard’s Lemma (for consumer), we know thatji ihj i j j i j h i ij s p u x p p u e p p u e p u x s =∂∂=∂∂∂=∂∂∂=∂∂=),(),(),(),(22p p p pHence S is symmetric. It is evident that S is the Hessian matrix of the expenditure function e (p , u ).Since we know that e (p , u ) is concave, so its Hessian matrix must be negative semidefinite.Since the second-order own partial derivatives of a concave function are always nonpositive, this implies that s ii ≤ 0, i.e.,i p u x s ih i ii ∀≤∂∂=,0),(pwhich indicates the intuitive property of a demand function: as its own price increases, the quantity demanded will decrease. You are reminded that this is a general property for Hicksian demands.For the Marshallian demands, note that by Slutsky equation,).,(),(),(),(y x yy x p u x p y x i i i h i i i p p p p ⋅∂∂-∂∂=∂∂Then for a small change in p i , we will have the following:.),(),(),(),(i i i i i h i i i i i p y x yy x p p u x p p y x x ∆⋅∂∂-∆∂∂=∆∂∂≈∆p p p pThe first item, capturing the own price effect of the Hicksian demands, is of course nonpositive.The sign of the second item depends on the nature of the good:• Normal good : ∂x i (p , y )/ ∂y > 0.• This leads to a normal Marshallian demand function: it is decreasing in its ownprice.• Inferior good : ∂x i (p , y )/ ∂y < 0.• When the substitution effect still dominates the income effect, the resultingMarshallian demand is also decreasing in its own price.• When the substitution effect is dominated by the income effect, it will lead to aGiffen good, that is, its demand function is an increasing function of its own price.Because of Slutsky equation, the Slutsky matrix (i.e., the substitution matrix) also has the following form that is in terms of Marshallian demand functions.⎥⎥⎦⎤⎢⎢⎣⎡∂∂+∂∂=⎥⎥⎦⎤⎢⎢⎣⎡∂∂==),(),(),(),(][y x y y x p y x p u x s j i j i j h i ij p p p p SWe will get back to the above Slutsky matrix in the next lecture when we discuss the integrability problem .3.5. The Elasticity Relations for Marshallian Demand FunctionsDefinition . Let x (p , y ) be the consumer’s Marshallian demand functions. Define.),(,),(),(,),(),(yy x p s y x p p y x y x yy y x i i i i jj i ij i i i p p p p p =∂∂=∂∂=εηThen1. ηi is called the income elasticity of demand for good i .2. ε ij is called the price elasticity of the demand for good i with respect to a price change ingood j . ε ii is the own-price elasticity of the demand for good i . For i ≠ j , ε ij is the cross-price elasticity .3. s i is called the income share spent on good i .The following result summarizes some important relationships among the income shares, income elasticities and the price elasticities.Proposition . Let x (p , y ) be the consumer’s Marshallian demand functions. Then1. Engel aggregation :.11=∑=mi ii s η2. Cournot aggregation :.,...,1 ,1m j s s j mi iji =-=∑=εProof . Both identities are derived from the Walras’ Law, namely, the fact that the budget is tight or balanced:y = p ⋅x (p , y ) for all p and y . (A)To prove Engel aggregation, we differentiate both sides of (A) w.r.t. y :∑∑∑====∂∂=∂∂=m i mi i i ii i i mi i i s y x yy y x y y x p y y x p 111,),(),(),(),(1ηp p p pas required.To prove Cournot aggregation, we differentiate both sides of (A) w.r.t. p j :.),(),(),(),(),(01∑∑=≠∂∂=-⇒∂∂++∂∂=mi j i i j jj jj ji j i ip y x p y x p y x p y x p y x p p p p p pMultiplying both sides by p j /y leads to∑∑∑====-⇒∂∂=∂∂=-mi iji j mi i jj i i i mi j j i i j j s s y x p p y x y y x p p p y x y p yy x p 111),(),(),(),(),(εp p p p pas required too.3.6 Hicks ’ Composite Commodity TheoremAny group of goods & services with no change in relative prices between themselves may be treated as a single composite commodity, with the price of any one of the group used as the price of the composite good and the quantity of the composite good defined as the aggregate value of the whole group divided by this price. Important use in applied economic analysis.Additional ReferencesAfriat, S. (1967) "The Construction of Utility Functions from Expenditure Data," International Economic Review, 8, 67-77.Arrow, K. J. (1951, 1963) Social Choice and Individual Values. 1st Ed., Yale University Press, New Haven, 1951; 2nd Ed., John Wiley & Sons, New York, 1963.Becker, G. S. (1962) "Irrational Behavior and Economic Theory," Journal of Political Economy, 70, 1-13.Cook, P. (1972) "A One-line Proof of the Slutsky Equation," American Economic Review, 42, 139. Deaton, A. and J. Muellbauer (1980) Economics and Consumer Behavior. Cambridge University Press, Cambridge.Debreu, G. (1959) Theory of Value. John Wiley & Sons, New York.Debreu, G. (1960) "Topological Methods in Cardinal Utility Theory," in Mathematical Methods in the Social Sciences, ed. K. J. Arrow and M. D. Intriligator, North Holland, Amsterdam. Diewert, W. E. (1982) "Duality Approaches to Microeconomic Theory," Chapter 12 in Handbook of Mathematical Economics, ed. K. J. Arrow and M. D. Intriligator, North Holland, Amsterdam.Gorman, T. (1953) “Community Preference Fields,” Econometrica, 21, 63-80.Hicks, J. (1946) V alue and Capital. Clarendon Press, Oxford, England.Katzner, D.W. (1970) Static Demand Theory. MacMillan, New York.Marshall, A. (1920) Principle of Economics, 8th Ed. MacMillan, London.McKenzie, L. (1957) “Demand Theory Without a Utility In dex," Review of Economic Studies, 24, 183-189.Pollak, R. (1969) "Conditional Demand Functions and Consumption Theory," Quarterly Journal of Economics, 83, 60-78.Roy, R. (1942) De l'utilite. Hermann, Paris.Roy, R. (1947) "La distribution de revenu entre les divers biens," Econometrica, 15, 205-225. Samuelson, P. A. (1938) "A Note on the Pure Theory of Consumer's Behavior," Econometrica, 5, 61-71, 353-354.Samuelson, P. (1947) Foundations of Economic Analysis. Harvard University Press, Cambridge, Massachusetts.Sen, (1970) Collective Choice and Social Welfare. Holden Day, San Francisco.Stigler, G. (1950) "Development of Utility Theory," Journal of Political Economy, 59, parts 1 & 2, pp. 307-327, 373-396.Varian, H. R. (1992) Microeconomic Analysis. Third Edition. W.W. Norton & Company, New York. (Chapters 7, 8 and 9)Wold, H. and L. Jureen (1953) Demand Analysis. John Wiley & Sons, New York.11。

公共支出
政府通过提供公共服务和基础 设施，弥补市场失灵，提高社 会福利。
监管和行政干预
政府对市场进行监管和行政干 预，防止垄断和不公平竞争。
市场失灵与政府干预的案例分析
环境污染案例
政府通过制定环保法规和排污标准，限制企 业排污，保护环境。
医疗保障案例
政府通过提供医疗保险和医疗救助，弥补市 场失灵，保障公民健康。
最优消费选择
在预算约束下，消费者选择能够最大化效用的商品组合。
边际替代效应
描述消费者在保持效用不变的情况下，一种商品对另一种商品的 替代程度。
消费者行为理论的扩展
风险偏好与不确定性
研究消费者在面临风险和不确定性时的消费行 为。
跨期消费选择
探讨消费者在不同时期之间的消费决策和储蓄 行为。
消费外部性
分析消费行为对其他个体或社会的影响，以及如何通过政策干预来改善消费行 为。
微观经济学的重要性
微观经济学是现代经济学的重要组成部分，它为政策制定者、企业家和消费者提供了理解和预测市场运作的基础 。通过研究微观经济学，人们可以更好地理解市场机制、价格体系和资源配置，从而做出更明智的决策。
微观经济学的基本假设和概念
基本假设
微观经济学通常基于一些基本假设， 如完全竞争、理性行为、完全信息等 。这些假设为理论分析提供了基础， 但在实际生活中可能并不完全成立。
公共选择理论与政治经济学
01
公共选择理论
研究公共物品和服务的供给和需求，以及政府决策的经济学分析。
02
政治经济学
研究政治和经济之间的相互作用，以及政治制度对经济发展的影响。
03
总结
公共选择理论和政治经济学是微观经济学的前沿领域，它们对于理解政

XIAMEN UNIVERSITY
SchoolofEconomics·WangYananInstituteforStudiesinEconomics
Advanced Microeconomics I
MIDTERM EXAMINATION
Fall, 2016
Instructions
• There are 4 questions in the exam. Please answer ALL of them. • Write your name, student ID, department and ALL answers on answer sheets. • NO calculator or references are allowed. • Any discussion or otherwise inappropriate communication between examinees, as
well as the appearance of any unnecessary material or cell phone usage, will be dealt with severely. • Good Luck!
Questions
1. Preference and Utility (25 marks) A consumer purchases two goods x1, x2 and his utility function is u(x1, x2) = [min(2x1 + x2, x1 + 2x2)]2 (a) Draw indifference curves on a graph. (3 marks) (b) Do the following properties hold for this utility function? Why? (i) Concave (3 marks) (ii) Quasi-Concave (3 marks) (iii) Homogeneous (If so, which degree?) (3 marks) (iv) Homothetic (3 marks) (c) Find the Marshallian demand for both goods. (7 marks) (d) Find the indirect utility function. (3 marks)

Department of EconomicsA DVANCED M ICROECONOMICS -Course Outline and Reading Guide Students who have solid background and are not adverse to a mathematical approach may use H.R. Varian, Microeconomic Analysis, Norton, 3rd edition, 1992. An alternative advanced text emphasizing game theory is David M. Kreps, A Course in Microeconomic Theory, Princeton University Press, 1990. Even more advanced texts includes:Andreu Mas-Colell, Michael D. Whinston and Jerry R. Green, 1995. Microeconomics Theory. Oxford University Press. (An advanced textbook in microeconomics theory.)However, the following texts are referred to frequently.Geoffery A. Jehle & Philip J. Reny (2001). Advanced Microeconomic Theory (2nd Edition). Boston: Addison-Wesley. (JR)Y.-K. Ng, Mesoeconomics: A Micro-Macro Analysis, London: Harvester, 1986.A simpler alternative to JR is:David G. Luenberger (1995). Microeconomic Theory. McGraw-Hill. (DL)The following topics are provided for reading. The lectures may not cover all topics and may not proceed in the same order.:(0) Mathematical Introduction (May be skipped if students are already familiar)JR: Ch. A1 & A2DL: Appendix C(1) Basic Consumer TheoryMainly on consumer preferences and the existence of utility functions, properties of demand functions, the composite commodity theorem, and the Slutsky equation.DL: Ch. 4JR: Ch. 1, 2, 3.Ng, Welfare Economics, App.1B.H.A.J. Green, Consumer Theory, Chapters 1-7P.R.G. Layard and A.A. Walters, Microeconomic Theory, McGraw-Hill, Sections 5.1 and 5.2Varian, Chapters 7-9(2) Some ExtensionsR.H. Frank, “If Homo Economicus could choose his own utility function, would he want one with a conscience?” American Economic Review, September 1987,593-604; June 1989, 588-596.Y.-K. Ng, “Step-optimization, secondary constraints, and Giffen goods”, Canadian Journal of Economics, November 1972, 553-560.Y.-K. Ng, “Diamonds are a government’s best friend: Burden-free taxes on goods valued for their values”, American Economic Review, March 1987, 77: 186-191.Y.-K. Ng, “Mixed diamond goods and anomalies in consumer theory: Upward-sloping compensated demand curves with unchanged diamondness”, Mathematical Social Sciences, 1993, 25: 287-293.(3) UncertaintyDL: Ch.11Gravelle & Rees, Chapters 19 and 20Green, Chapters 13, 14 & 15Y.-K. Ng, “Why do people buy lottery tickets? Choices involving risk and the indivisibility of expenditure”, Journal of Political Economy, October 1965, 530-535.Varian, Chapter 11Y.-K. Ng, “Expected subjective utility: Is the Neumann-Morgenstern utility the same as the neoclassical’s?” Social Choice Welfare, 1984, pp. 177-186.(4) Production and Marginal Productivity TheoriesDL: Ch. 5JR: Ch. 2, 3.Baumol, Chapter 11Henderson & Quandt, Chapter 3Varian, Chapters 1-5R.H. Frank, “Are workers paid their marginal products”, American Economic Review, 1984, 549-571.L. Borghans & L. Groot, “Superstardom and monopolistic power: Why media stars earn more than their marginal contribution to welfar e”, Journal of Institutional and Theoretical Economics, 1998, pp.546-(5) Introduction to Mesoeconomic AnalysisY.-K. Ng, Mesoeconomics: A Micro-Macro Analysis, London: Harvester, 1986.Y.-K. Ng, “Business confidence and depression prevention: A meso economic perspective”, American Economic Review, May 1992, 82(2): 365-371.Ng, “Non-neutrality of money under non-perfect competition: why do economists fail to see the possibility?” In Arrow, Ng, and Yang, eds., Increasing Returns and Economic Analysis, London: Macmillan, 1998, pp.232-252.(6) General EquilibriumDL: Ch. 7; JR: Ch.5K.J. Arrow & F. Hahn (1971), General Competitive Analysis, Chapter 1F. Black (1995), Exploring General Equilibrium, Cambridge, Mass.: MIT Press.J.S. Chipman, “The nature and meaning of equilibrium in economic theory”, in D.Martindale, ed., Functionalism in Social Sciences; reprinted in H. Townsend, ed., Price Theory, Penguin.Gravelle & Rees, Chapter 16W. Nicholson, Appendix B to Chapter 19, “The existence of genera l equilibrium prices”, Microeconomic Theory, 1985, The Dryden Press, 684-694.Starr. R.M. (1997). General Equilibrium Theory: An Introduction. Cambridge University Press.Varian, Chapters 17 & 21S. Zamagni, Microeconomic Theory. Oxford: Blackwell, 1987, Ch. 16.(7) Selected Topics in Microeconomic Analysis(a)Adverse selection, signalling, and screening.Akerlof, G. “The market for lemons: quality uncertainty and the market mechanism”, Quarterly Journal of Economics, 1970, 89: 488-500.Mas-Colell, Andreu, Whinston, Michael D. & Green, Jerry R., Microeconomic theory New York : Oxford University Press, 1995, Ch. 13.(b)The principal-agent problemHolmstrom, B., (1979), “Moral hazard and Observability”, Bell Journal of Economics, 10(1), 74-91Mas-Colell, Andreu, Whinston, Michael D. & Green, Jerry R., Microeconomic theory New York : Oxford University Press, 1995, Ch. 14.3typescript.(h) Specialization and Economic OrganizationYang, Xiaokai, Economics: New Classical versus Neoclassical Frameworks, Blackwell, 2001, Chs.5-7, 11.Yang, Xiaokai & Ng, Y.-K. Specialization and Economic Organization: A New Classical Microeconomic Framework. In "Contributions to Economic Analysis", V ol. 215, 1993, Amsterdam: North Holland, pp. xvi + 507. (Mainly Chs.0-2, 5.)Yang, X iaokai & Ng, Siang, “Specialization and Division of Labour: A Survey”, in Kenneth J. Arrow, et al, eds., Increasing Returns and Economic Analysis, London: Macmillan, 1998, pp. 3-63.Yang, Xiaokai & Ng, Y.-K. “Theory of the Firm and Structur e of Residual Rights”, Journal of Economic Behaviour and Organization, V ol. 16, pp. 107-28, 1995.(i)Does the enrichment of a sector benefit others?Ng, "The Enrichment of a Sector (Individual/Region/Country) Benefits Others: The Third Welfare Theorem?", Pacific Economic Review, Nov. 1996, V ol. 1, No.2, pp.93-115.Ng, Siang & Y.-K., “The enrichment of a sector(individual/region/country) benefits others: a generalization”, Pacific Economic Review, Oct. 2000, 5(3): 299-302.Ng, Siang & Y.-K., “The enrichmen t of a sector(individual/region/country) benefits others: the case of trade for specialization”, International Journal of Development Planning Literature, 1999, 14(3): 403-410.。

Overview of the inframarginal analysisWhy economists shifted their attention from the economic organization problem to the resources allocation problem?1)David Ricardo's concept of comparative advantage∙Exogenous comparative advantage∙Endogenous comparative advantage:Smith’s concept of economies of the division of labourComparative advantage may exist between ex ante identicalif they choose different levels of specialization in producing different goodsif there exist increasing returns to specialization2)Marshall's neoclassical framework∙The dichotomy between pure consumers and firms∙The replacement of the concept of economies of specialization with the concept of economies of scale∙The marginal analysis of demand and supply.(Ma rshall’s neoclassical framework cannot be used to analyse individuals’ decisions in choosing levels and patterns of specialization, so that the structure of division between pure consumers and firms is exogenously given)Two types of trade-offs:Neoclassical trade-off --- the trade-off between the production and consumption of all different goods and services given the degree of scarcity of resources; (the problem of allocation of scarce resource)Classical trade-off --- the trade off between transaction costs andthe economies of specialization facilitated by the division of labour (the problem of economic organization)(a) Neoclassical framework (b) Flow chart in neoclassical economicsFigure 1: Neoclassical Analytical FrameworkNew Classical Economics (Yang-Ng framework)New classical general equilibrium model endogenizes individual's level of specialization and the level of division of labour for society as a whole within a framework with:1)consumer-producers2)economies of specialization3)transaction cosst4)corner solutions(a) Autarky (b) Partial division of labor (c) Complete division of labor Fig.2: New Classical Analytical FrameworkA simple model of inframarginal analysis:An economy has M ex ante identical individual who are both consumer and producers Two consumption goods X and YEach consumer-producer has the following utility function.(1) u x kx y ky d d=++()()Each consumer-producer’s production functions and endowment constraint are (2a)x x l sx a+=,y y l sy a+=,a > 1(2b)l l x y +=1.Each consumer-producer’s budget constraint is(3) p x p y p x p y x s y s x d y d+=+p i is the price of good i. The left hand side of (3) is income from the market and the right hand side is expenditure. Corner solutions are allowed and we have the non-negativity constraints(4) x, x s , x d , y, y s , y d , l x , l y ≥ 0.Each consumer-producer maximizes utility in (1) with respect to x, x s , x d , y, y s , y d , l x , l y subject to the production conditions given by (2), the budget constraint (3), and the non-negativity constraint (4). Since l x and l y are not independent of the values of the other decision variables, each of the 6 decision variables x, x s , x d , y, y s , y d can take on 0 and positive values. When a decision variable takes on a value of 0, a corner solution is chosen.Individual decision problemsThere are 64223=x solutions include 63 corner solutions and one interior solution for each consumer and producer.Using the theorem of specialization narrows down the set of candidates for the optimum decisionsTheorem of Optimal Configurations: The optimum decision does not involve selling more than one goods, does not involve selling and buying the same good, and does not involve buying and producing the same good.(Implications: interior solution can never be optimal, the marninal analysis for interior solution does not work for the new classical framework)This theorem, together with the budget constraint and the requirement that utility be positive, can be used to reduce the number of candidates for the optimum decision radically from 64 to only 3.The theorem is intuitive. Selling and buying the same good involves unnecessary transaction costs and therefore is inefficient. Selling two goods is also inefficient since it prevents the full exploitation of economies of specialization.The list of candidates for the optimum corner solutionTable 1: Profiles of Zero and Positive Valuesof the 6 Decision Variablesx x d x s y y d y s+ + + + + +0 + + 0 + +0 + 0 0 + ++ 0 0 0 + +∙∙∙∙∙∙+ 0 0 0 0 +0 0 0 0 0 +Three configurations(i) Autarky, or configuration A, is defined byx y l l x y ,,,>0, x x y y s d s d====0The decision problem for configuration A is (5a)xy u yx l l y x =,,,:Max s.t. x l x a=, y l y a=, l l x y +=1.Inserting all constraints into the utility function (5.5a) can be converted to the following non-constrained maximization problem. (5b)ax ax ll l u x)1(:Max -=totally differentiate u with respect to l x(6)0d d d d d d =+=xx x l yy u l x x u l u ∂∂∂∂the corner solution for configuration A is(7) 5.0**==y x l l ∂==5.0**y x u a()A =-22Two configurations of specialization:(ii) Configuration B : configuration with specialization is (x/y), specializationin producing good x, selling x and buying y.It is defined by x, x s , y d , l x > 0, x d = y s = y = l y = 0. This definition, together with (1)-(4), can be used to specify the decision problem for this configuration.(8) M ax:x x xds d u xky ,,=s.t.x x l sx a+=, l x =1 (production conditions)p y p x y dx s= (budget constraint)Plugging the constraints into the utility function to eliminate l x , x , and y d yields the nonconstrained maximization problem(9)M ax: xsx sysu x k p x p =-()1The corner solution for configuration (x/y) is(10) x s = 0.5, y d = p x x s /p y = p x /2p y , u x = kp x /4p y .(iii) Configuration C: configuration with specialization is (y/x), in which theindividual sells good y and buys good x, is defined by y, y s , s d , l y > 0, y d = x s = x = l x = 0. The decision problem for this configuration is:(11)M ax :y y xds d u ykx ,,= s.t.y y l sy a+==1(production condition)p y p x y sx d=(budget constraint)Following the procedure used in solving for the corner solution for configuration (x/y), the corner demand and supply functions and corner indirect utility function for configuration (y/x) is solved as follows:(12) y s = 0.5, x d = p y /2p x , u y = kp y /4p x .Table 2: Three Corner SolutionsStructures and Corner equilibriaThere are two organization structures:Structure A (Autarky)Structure D (Division of labour): A combination of configurations B and C.Let the number (measure) of individuals choosing (x/y) be M x and the number choosing (y/x) be M y.There is a corner equilibrium for each structure.The market clearing and utility equalization conditions are established by free choice between configurations and utility maximization behavior.In structure D, the corner equilibrium relative price of traded goods is:u kp p kp p u x yy yx y ===44or1=xyp pthe market demand for good x is X d ≡ M y x d = M y p y / 2 p x ,the market supply of good x is X s ≡ M x x s = M x / 2The market clearing condition for good x isX d = M y p y /2p x = X s = M x /2, or p x /p y = M y /M xThe corner equilibrium in structure D isp x /p y = 1, M x = M y = M /2.x = y = x s = y s = x d = y d = ½, u D = k /4Table 3: Two Corner EquilibriaGeneral equilibrium and its comparative staticsProposition 1:The corner equilibrium that generates maximum per capita real income is the full equilibriumProposition 2: Equilibrium is the division of labour if )1(202a k k -≡> and is autarkyif )1(202a k k -≡<Proposition 3:A sufficient improvement in transaction efficiency generates the concurrence of progress in labour productivity and the increases in the level of specialization, in the level of division of labour, the degree of market integration, the degree of interdependence, and the degree of commercialisation.( b ) Structure D, division of laborFigure 2: Autarky and Division of LaborTwo types of comparative statics:1)inframarginal comparative statics of general equilibrium across the structuresexplain the relationship between economic growth and economic organization2)marginal comparative statics of corner equilibrium within each given structure.New classical theory analyses both the adjustments within a given structure of economic organization and changes in economic orgainization.Welfare implications of EquilibriumThe first welfare theorem:In a new classical model with ex ante identical consumer-producers, each corner equilibrium is locally Pareto optimal for the given structure and the general equilibriumis globally Pareto optimal.Implication: corner equilibrium is allocationally efficient, the general equilibrium is both organizationally efficient and allocationally efficient.Consider structure D:Let X i = {x i, x i s, y i d} be the decision of individual i choosing configuration (x/y)Y j ={y j, y j s, x j d} be the decision of individual j choosing configuration (y/x).the corner equilibrium values of X i and Y i as X i* and Y i*, respectively, and the corner equilibrium price of good x in terms of good y as p.Suppose that the corner equilibrium in structure D is not locally Pareto optimal. Then there exists an allocation X i, Y i in structure D such that(2a) u i ( X i ) ≥u i(X i*) for all i, and u i ( X i ) > u i(X i*) for some i(2b) u j ( Y j ) ≥u j(Y j*) for all j.Thi s implies that a benevolent central planner can increase at least one individual’s utility without reducing all others’ utilities by shifting the decisions from {X i*, Y i*} to {X i, Y i}. That is, the corner equilibrium decisions {X i*, Y i*} are not locally Pareto optimal.Since utility is a strictly increasing function of consumption, the generalized axiom of revealed preference and (2a) implies(3a) p x x i s ≤p y y i d for all i and p x x i s < p y y i d for some iand (2b) implies(3b) p y y j s ≤p x x j d for all j.Adding up the above inequalities for all individuals yieldsp x∑i x i s < p y∑i y i d and p y∑j y j s ≤p x∑j x j d or(4) (p x / p y )∑i x i s < ∑i y i d and ∑j y j s ≤(p x / p y )∑j x j d(4), together with the market clearing condition for good y, ∑i y i d = ∑j y j , yields∑i x i s <∑j x j dThis violates the material balance condition for good x and therefore establishes the claim that the Pareto superior allocation X i and Y i are infeasible. Hence, the corner equilibrium in D, X i* and Y i*, must be locally Pareto optimal.The distinctive features of equilibrium in Yang-Ng frameworkAggregate demand and supply can be endogenized in the Yang-Ng framework∙the outcome of interactions between the self-interested decisions of individuals in choosing their levels of specialization will determine the network size of division of labor for society as a whole.∙The pattern and size of the network of division of labor in turn determine demand and supplyDisparity between the Pareto optimum and PPFThe PPF in neoclassical models is associated with the Pareto optimumbecause the convex aggregate production set is a simple sum of convex individual production sets, and a central planner’s solution for the maximization of total profit of all firms is equivalent to decentralized profit maximization of each individual firm.The PPF in the new classical model may not be associated with the Pareto optimum.Example: general equilibrium structure is A, which is Pareto optimal, if k < k0. But the PPF is associated with structure D, not with structure A.because in the new classical framework, there are multiple production subsets associated with different structures. The PPF is the highest of them.Implications: the equilibrium aggregate productivity, the degree of scarcity and the comparative advantages are endogenized in the new classical.The application of Yang-Ng framework:New Classical Trade TheoryNew Classical Theory of the FirmNew Classical Urban Economics and New Classical Theories of industrialization and HierarchyNew Classical Growth ModelsNew Classical Theory of Contract and Property RightsETC.。

课程大纲高级微观经济学（经济类）Advanced Microeconomics课程编号：02810090 授课对象：研究生学分：3 任课教师：孟涓涓课程类型：必修开课学期：2017年秋季先修课程：上课时间：5-12周，每周两次课周二2-4节（09:00-12:00）周三5-7节（13:00-16:00）第一次上课时间：2017年10月10日上课地点：光华老楼202任课教师简历（500字左右）：孟涓涓，现任北京大学光华管理学院应用经济系和金融系副教授，她在美国加州大学获得经济学博士学位。

孟涓涓目前的研究专长包括行为经济学，行为金融学，劳动经济学，发展经济学等。

她的研究成果发表在国外顶级学术期刊上，如American Economic Review, Journal of Public Economics, Journal of Development Economics, International Economic Review, Games and Economic Theory, Journal of Economic Behavior and Organization.她目前主持国家自然科学基金面上项目“参照点和狭隘视野：行为经济学前沿问题探究” 和北京青年英才计划"依赖人际关系还是正式渠道---论正式与非正式制度安排对社会经济发展的影响"项目研究。

曾经主持国家自然科学基金青年基金研究项目“个体经济行为中的社会性因素”（已结题）。

孟博士曾获奖项有：光华管理学院最佳新人奖，2007-2008Excellence in Referee Reward, The American Economics Review,2001-2004北大明德奖学金等。

任课教师联系方式：Email: jumeng@电话：62754669助教姓名及联系方式：马骁: pkumaxiao@朱妮：zhuni@辅导、答疑时间：周三上午11-12点，光华新楼320.一、课程概述本课是微观经济学的研究生课程，内容涵盖经典微观经济学理论，包括消费者理论、生产者理论、市场均衡、外部性等，同时涉及行为经济学等前沿理论发展。

《高级微观经济学》教学大纲“Advanced Microeconomics” Course Outline课程编号：151193A课程类型：专业选修课总学时：48 讲课学时：48学分：3适用对象：经济学、统计学、金融学先修课程：经济学原理、中级微观经济学、线性代数、微积分Course Code: 151193ACourse Type: Specialized elective coursePeriods: 48 Lecture: 48Credits: 3Applicable Subjects: Economics, Statistics, FinancePreparatory Courses: Principles of Microeconomics, Introductory Microeconomics, Linear Algebra, Mathematical Analysis一、课程的教学目标本课程作为本科学生的专业选修课旨在通过介绍微观经济学中的主要模型、原理和证明使学生具备进行微观经济学研究的基本方法与技能,为后续专业课程的学习奠定基础。

This specialized elective course is offered to undergraduate students majoring in Economics, Statistics, and Finance. This course builds the foundation for the study of subsequent major courses and trains the students in the micro – economic research skills.二、教学基本要求本课程的教学内容大致可以分为四大部分。

第一部分为个人决策理论。

第二部分为博弈论。

第三部分为市场均衡和市场失效理论。

第四部分为一般均衡理论。

Advanced MicroeconomicsTopic 1: Set, Topology, Real Analysis and Optimization Readings: JR - Chapters 1 & 2, supplemented by DL - Appendix C1.1 IntroductionIn this lecture, we will quickly go through some basic mathematical concepts and tools that will be used throughout the rest of the course. As this is a review session, the attention will be mainly on refreshing on the language, style and rigor of mathematical reasoning. In economic analysis, especially microeconomic analysis, mathematics is always treated as a tool, never the end. On the other hand, by integrating economics with rigorous mathematics, we will be able to develop the theoretical expositions in a sound and logical manner, which is why economics is also known as economic science. Not many other traditionally known as social science fields manage to pass this critical stage. But it is important to remember that as an economist, we must go beyond the normal mathematical treatment and the underlying economics and their policy implications are far more important and interesting.The plan of this lecture goes like this. First, we will review the basic set theory. We then move on to a bit of topology. After reviewing basic elements of real analysis, we will cover some key results in optimization.1.2 Basics of Set Theory 1.2.1 B asic Concepts∙ set : a collection of elements∙ sets operations : union, intersection ∙ real sets : n n +R R R , , (the notion of vectors)∙ ∀ : for any; ∃ : there exists; ∍ : such that; ∈ : belongs to; is an element of1.2.2 C onvexity & RelationsConvex Set:∙ A set S ⊂ R n is convex if .10 and ,,)1(2121≤≤∈∀∈-+t S S t t x x x x∙ Intuitively, a set is a convex set if and only if (iff) we can connect any two points in a straightline that lies entirely within the set.∙ Convex set has no holes, no breaks, no awkward curvatures on the boundaries; they areconsidered as “nice sets”.∙ The intersection of two convex sets remains convex.Relations∙ For any two given sets, S and T , a binary relation R between S and T is a collection ofordered pairs (s , t ) with s ∈S and t ∈T .∙ It is clear that R is a subset of S ⨯ T : (s , t ) ∈ R or s R t .Properties of Relations :∙ Completeness∙ R ⊂ S ⨯ S is complete iff for all x and y (x ≠ y ) in S , x R y or y R x .∙ Reflexivity∙ R ⊂ S ⨯ S is reflexive if for all x in S , x R x .∙ Transitivity∙ R ⊂ S ⨯ S is transitive if for all x, y, z in S , x R y and y R z implies x R z .1.3 TopologyTopology attempts to study the fundamental properties of sets and mappings. Our discussion will be mainly on the real space R n .∙ A real topological space is normally denoted as (R n , d ), where d is the metric defined on thereal space. Intuitively speaking, d is a distance measure between two points in the real space. ∙ Euclidean spaces are special real topological spaces associated with the Euclidean metricdefined as follows:n n n x x x x x x d R x x x x x x ∈∀-++-+-=-=2122122212221112121,;)()()(||||),(1.3.1 S ets on a Real Topological Spaceε-Balls∙ Open ε-Ball for a point x 0: for ε > 0,}),(|{)(00εε<∈≡x x R x x d B n∙ Closed ε-Ball for a point x 0: for ε > 0,}),(|{)(00εε≤∈≡x x R x x d B nOpen Sets∙ S ⊂ R n is open set if, ∀ x ∈ S , ∃ ε > 0 such that (∍) B ε(x ) ⊂ S . ∙ Properties of Open Sets:∙ The empty set and the whole set are open set∙ Union of open sets is open; intersection of open sets is open too. ∙ Any open set can be represented as a union of open balls:)(x x x εB S S∈= , where S B ⊂)(x x ε.Closed Sets∙ S is a closed set if its complement, S c , is an open set.∙ A point x ∈S is an interior point if there is some ε-ball centered at x that is entirely containedin S . The collection of all interior points of S is denoted by int S , known as the interior of S .∙ Properties of Closed Sets:∙ The empty set and the whole set are closed;∙ Union of any finite collection of closed sets is a closed set; ∙ Intersection of closed sets is a closed set.Compact Sets∙ A set S is bounded if ∃ ε > 0 such that (∍): S ⊂ B ε(x ) for some x ∈ S . ∙ A set in R n that is closed and bounded is called a compact set .1.3.2 F unctions/Mappings on R n∙ Let D ⊂ R m , f : D → R n . We say f is continuous at the point x 0 ∈D if∀ ε > 0, ∃ δ > 0 ∍ ))(())((00x x f B D B f εδ⊂⋂∙ Special Case: D ⊂ R , f : D → R . f is continuous at x 0 ∈D if ∀ ε > 0, ∃ δ > 0 ∍ δε<-∈<-|| and whenever ,|)()(|00x x D x x f x fProperties of Continuous Mappings:∙ Let D ⊂ R m , f : D → R n . Then∙ f is continuous ⇔ for all open ball B ⊂ R n , f --1(B ) is open in D⇔ for all open set S ⊂ R n , f --1(S ) is open in D∙ If S ⊂ D is compact (closed and bounded), then its image f (S ) is compact in R n .1.3.3 W eierstrass Theorem & The Brouwer Fixed-Point TheoremThese two theorems, known as existence theorems , are very important in microeconomic theory. “An existence theorem” specifies conditions that, if met, something exists . In the meantime, please keep in mind that the conditions in the existence theorems are normally sufficient conditions , meaning that if the required conditions are NOT met, it does not mean the nonexistence of something – it may still exist. The existence theorems say very little about exact location of this something . In other words, existence theorems are powerful tools for showing that something is there; but it is not sufficient in actually finding the equilibrium.Weierstrass Theorem – Existence of Extreme Values∙ This is a fundamental result in optimization theory .∙ (Weierstrass Theorem ) Let f : S ⊂ R be a continuous real-valued mapping where S is a nonemptycompact subset of R n . Then a global maximum and a global minimum exist, namely,.),~()()( that such ~,**S f f f S S ∈∀≤≤∈∈∃x x x x x xThe Brouwer Fixed-Point TheoremMany profound questions about the fundamental consistency of microeconomic systems have been answered by reformulating the question as one of the existence of a fixed point. Examples include:∙ The view of a competitive economy as a system of interrelated markets is logically consistentwith this setting;∙ The well-known Minimax Theorem in game theory∙ (Brouwer Fixed-Point Theorem ) Let S ⊂ R n be a nonempty compact and convex set. Let f : S→ S be continuous mapping. Then there exists at least one fixed point of f in S . That is, ∃ x * ∈S such that x * = f (x *).1.4 Real-Valued Functions∙ By definition, a real-valued function is a mapping from an arbitrary set D (domain set ) of R n to a subsetR of the real line R (range set ).∙ f : D → R , with D ⊂ R n & R ⊂ R.Increasing/Decreasing Functions:∙ Increasing function : f (x 0) ≥ f (x 1) whenever x 0 ≥ x 1;∙ Strictly increasing function : f (x 0) > f (x 1) whenever x 0 > x 1;∙ Strongly increasing function : f (x 0) > f (x 1) whenever x 0 ≠ x 1 and x 0 ≥ x 1∙ Similarly, we can define the three types of decreasing functions.Concavity of Real-Valued Functions∙ Assumption f : D → R , with D ⊂ R n is convex subset of R n & R ⊂ R.∙ f : D → R is concave if for all x 1, x 2 ∈ D ,]1 ,0[),()1()())1((2121∈∀-+≥-+t f t tf t t f x x x x∙ Intuitively speaking, a function is concave iff for every pair of points on its graph, the chordbetween them lies on or below the graph.∙ f : D → R is strict concave if for all x 1≠ x 2 in D ,)1 ,0(),()1()())1((2121∈∀-+>-+t f t tf t t f x x x x∙ f : D → R is quasiconcave if for all x 1, x 2 ∈ D ,]1 ,0[)],(),(min[))1((2121∈∀≥-+t f f t t f x x x x∙ f : D → R is strictly quasiconcave if for all x 1≠ x 2 in D ,)1 ,0()],(),(min[))1((2121∈∀>-+t f f t t f x x x xConvexity of Real-Valued Functions∙ After the discussion of concave functions, we can take care of the convex functions by taking thenegative of a concave function.∙ f : D → R is convex if for all x 1, x 2 ∈ D ,]1 ,0[),()1()())1((2121∈∀-+≤-+t f t tf t t f x x x x∙ f : D → R is strict convex if for all x 1≠ x 2 in D ,)1 ,0(),()1()())1((2121∈∀-+<-+t f t tf t t f x x x x∙ f : D → R is quasiconvex if for all x 1, x 2 ∈ D ,]1 ,0[)],(),(min[))1((2121∈∀≤-+t f f t t f x x x x∙ f : D → R is strictly quasiconvex if for all x 1≠ x 2 in D ,)1 ,0()],(),(min[))1((2121∈∀<-+t f f t t f x x x xProperties of Concave/Convex Functions∙ f : D → R is concave ⇔ the set of points beneath the graph, i.e., {(x , y )| x ∈ D , f (x ) ≥ y } is a convexset.∙ f : D → R is convex ⇔ the set of points above the graph, i.e., {(x , y )| x ∈ D , f (x ) ≤ y } is a convex set. ∙ f : D → R is quasiconcave ⇔ superior sets, i.e., {x | x ∈ D , f (x ) ≥ y } are convex for all y ∈ R . ∙ f : D → R is quasiconvex ⇔ inferior sets, i.e., {x | x ∈ D , f (x ) ≤y } are convex for all y ∈ R .∙ If f is concave/convex ⇒ f is quasiconcave/quasiconvex;∙ f (strictly) concave/quasiconcave ⇔ -f (strictly) convex/quasiconvex.∙ Let f be a real-valued function defined on a convex subset D of R n with a nonempty interior on which f isa twice differentiable function, then the following statements are equivalent: ∙ If f is concave.∙ The Hessian matrix H (x ) is negative semidefinite for all x in D . ∙ For all x 0 ∈ D , f (x ) ≤ f (x 0) + ∇ f (x 0) (x – x 0), ∀ x ∈ D .Homogeneous Functions∙ A real-valued function f (x ) is called homogeneous of degree k if0 all for )()(>=t f t t f k x x .Properties of Homogeneous Functions:∙ f is homogeneous of degree k , its partial derivatives are homogeneous of degree k – 1. ∙ (Euler’s Theorem) f (x ) is homogeneous of degree k iff. all for )()(1x x x ∑=∂∂=ni i ix x f kf1.5 Introduction to Optimization∙ We will focus on real-valued functions only.Main Concepts of Optima∙ Local minimum/maximum ∙ Global minimum/maximum∙ Interior maxima, boundary maxima 1.5.1 U nconstrained OptimizationFirst-Order (Necessary) Condition for Local Interior Optima∙ If the differentiable function f (x ) reaches on a local interior maximum or minimum at x *, then x *solves the system of simultaneous equations:∇ f (x *) = 0.Second-Order (Necessary) Condition for Local Interior OptimaLet f (x ) be twice differentiable.1. If f (x ) reaches a local interior maximum at x *, then H (x *) is negative semidefinite.2. If f (x ) reaches a local interior minimum at x *, then H (x *) is positive semidefinite.Notes:∙ There is a simple method in checking whether a matrix is a negative (positive) semidefinte,which is to examine the signs of the determinants of the principle minors for the given matrix.Local-Global Optimization Theorem∙ For a twice continuously differentiable real-valued concave function f on D , the following threestatements are equivalent, where x* is an interior point of D : 1. ∇ f (x*) = 0.2. f achieves a local maximum at x*.3. f achieves a global maximum at x*.Strict Concavity/Convexity and Uniqueness of Global Optima∙ If x * maximizes the strictly concave (convex) function f , then x * is the unique global maximizer(minimizer).1.5.2 C onstrained OptimizationThe Lagrangian MethodConsider the following optimization problem:m j g f j n,,1,0)( subject to )(max ==∈x x RxNote:∙ If the objective function f is real-valued and differentiable, and if the constraint set defined bythe constraint equations is compact, then according to Weierstrass Theorem, optima of the objective function over the constraint set do exist.To solve this, we form the Lagrangian by multiplying each constraint equation g i by a different Lagrangian multiplier λj and adding them all to the objective function f . Namely,∑=+=mj j j g f L 1).()(),(x x Λx λLagrange’s TheoremLet f and g j be continuously differentiable real-valued function over some D ⊂ R n . Let x * be an interior point of D and suppose that x * is an optimum (maximum or minimum) of f subject to the constraints, g j (x *) = 0, j = 1, …, m . If the gradient vectors, ∇ g j (x *), j = 1, …, m , are linearly independent, then there exist m unique numbers λ, j = 1,…, m , such that.,...,1for 0 )()(),(1**n i x g x f x L m j ij j i i ==∂∂+∂∂=∂Λ∂∑=x x x λSpecial Case: Graphical InterpretationConsider the special case: max f (x 1, x 2) subject to g (x 1, x 2) = 0.As our primary interest is to solve the problem for x 1, x 2, then the Lagrangian condition becomes:21212211*x g x g x f x f x g x f x g x f ∂∂∂∂-=∂∂∂∂-⇒∂∂∂∂-=∂∂∂-=λ which is what we commonly known as tangency condition . To see this, define the level set as follows:L (y 0) = {(x 1, x 2) | f (x 1, x 2) = y 0}.and refer the diagram below.Second-Order Condition & Bordered HessianFor ease of discussion, let us focus the special case: max f (x 1, x 2) subject to g (x 1, x 2) = 0. Assume that there is a (curve) solution to the constraint, namely, x 2 = x 2(x 1), such thatg (x 1, x 2(x 1)) = 0Lettingy = f (x 1, x 2(x 1))be the value of the objective function subject to the constraint.∙ As a function of single variable, the second-order (sufficient) condition for a maximum/minimum is thatthe second-order derivative of y with respect to x 1 is negative (concave) or positive (convex).∙ This second-order derivative is associated with the determinant of the following matrix, known asbordered Hessian of the Lagrange function L :⎪⎪⎪⎭⎫ ⎝⎛=0212222111211g g g L L g L L H ∙ In particular, we have the following relationship:22212)()1(g D dx y d -= where D is the determinant of the bordered Hessian, i.e.,])(2)([0212221122211212222111211g L g g L g L g g g L L g L L D +--== ∙ The above discussion can be extended to the general case.Inequality ConstraintsLet f (x ) be continuously differentiable.∙ If x* maximizes f (x ) subject to x ≥ 0, then x satisfies:ni x n i x f x n i x f i i i i ,...,1 ,0,...,1 ,0*)(,...,1 ,0*)(**=≥==⎥⎦⎤⎢⎣⎡∂∂=≤∂∂x x∙ If x* mimimizes f (x ) subject to x ≥ 0, then x satisfies:ni x n i x f x n i x f i i i i ,...,1 ,0,...,1 ,0*)(,...,1 ,0*)(**=≥==⎥⎦⎤⎢⎣⎡∂∂=≥∂∂x xKuhn-Tucker Conditions(Kuhn-Tucker) Necessary Conditions for Optima of Real-Valued Functions Subject to Inequality Constraints:Let f (x ) and g j (x ), j = 1,…,m , be continuously differentiable real-valued functions over some domain D ⊂ R n . Let x * be an interior point of D and suppose that x * is an optimum (maximum or maximum) of f subject to the constraints, g j (x ) ≥ 0, j = 1,…,m .If the gradient vectors ∇ g j (x*) associated with all binding constraints are linearly independent, then there exists a unique vector Λ* such that (x*, Λ*) satisfies the Kuhn-Tucker conditions:.,...,1 0*)( ,0*)( ,...,1 0*)(*)(*)*,(*1*m j g g ni x g x f L j j j m j i j j i i =≥===∂∂+∂∂≡Λ∑=x x x x x λλ Furthermore, the vector Λ* is nonnegative if x* is a maximum, and nonpositive if it is a minimum.1.5.3 V alue FunctionsConsider the following parameterized optimization problem:max {x } f (x, a ) subject to g (x, a ) = 0 and x ≥ 0.where x is a vector of choice variables, and a = (a 1, …, a m ) is a vector of parameters that may enter the objective function, the constraint, or both.∙ Suppose that for each a , there is a unique solution denoted by x(a).∙ Define the value function M (a ) = f (x(a), a ), which is the optimal value of the objective functionassociated with a .The Envelope TheoremConsider the same optimization problem as identified above. For each a , let x(a). > 0 uniquely solve the problem. Assume that the objective function and the constraints are continuously differentiable in the parameters a . Let L (x,a,λ) be the problem's associated Lagrangian function and let (x(a), λ(a )) solve the Kuhn-Tucker conditions. And let M (a ) be the problem's associated maximum-value function. Then, the Envelope Theorem states that.,...,1 )()(),(m j a La M jj =∂∂=∂∂a a x a λNote:∙ The theorem says that the total effect on the optimized value of the objective function when aparameter changes (and so, presumably, the whole problem must be reoptimized) can bededuced simply by taking the partial of the problem's Lagarangian with respect to the parameter and then evaluating that derivative at the solution to the original problem's first-order Kuhn-Tucker conditions.The theorem applies to cases having many constraints.。

高级微观经济学课本：参考书：1)Andreu Mas-Colell，Michael D. Whinston andJerry R. Green，1995，Microeconomic Theory，Oxford University Press；2)Hal Varian，Microeconomic Analysis，中译本，中译本：《微观经济理论》，经济科学出版社3)平新乔，微观经济学18讲，北京大学出版社1第一章：消费理论1.基本概念2.偏好关系和效用函数3.消费者的优化问题4.间接效用函数和支出最小化5.需求的特征本章属于经典消费理论。

其中大多数原理我们已经在中初级微观经济学中学习过。

但是在那里，这些原理来自于生活经验的归纳，而没有严格的证明。

本章的内容是严格的从消费者偏好开始通过数学推导出整个经典消费理论。

由于生产者和消费者是一对对偶，在行为上非常相似，因此，2有了严格建立在数学推导上的消费者理论和生产者理论就为整个微观经济学科学性有了保障。

本章的学习，重点在于理解现代微观经济学是如何从消费者偏好——效用函数——选择——需求建立起科学的消费者理论的。

34 1.1基本概念1、选择集/消费集X定义：所有可能的（能实现的和不能实现的）消费（选择）方案x 的集合。

消费方案x ：商品：1) 商品数量无限可分： i x ∈ ，商品数量是连续的。

2) 商品数量非负：i x +∈3) 商品种类为：n消费束/组合（向量）：()1,...,nn x x X +=∈=x5消费集X 特征：1、 非空集2、 闭集：p.429，定义A1.11（边界上的点能达到）3、 凸集：P.411，A1.2.24、 包含原点：X2、可行集B ：制度约束、经济约束等3、偏好关系4、行为假设:在各种能够实现的消费方案中，消费者选择他最偏好的消费方案。

6 1.2、偏好关系和效用函数Debreu (1959)问题：1、无差异曲线为什么是我们常见的那种形状？2、怎样用一个函数描述偏好关系？1、偏好关系①、关系、两元关系：p.415-p.416 ②、两元关系的定义：定义在消费集X 上，反映X 中任意两个点之间的关系：12,X x x ，如果有12x x，则对该消费者而言，“1x 至少和2x 一样好”，或者，“在1x 和2x 之间，消费者弱偏好1x ”7公理一：完备性公理：对于选择集X 中任意的两个要素1x和2x ，有12x x 或21x x 含义：◆ 消费者能够做出对任何两个消费组合进行比较 ◆ 消费者具有无限的认知能力◆ 消费者具有无限的判断能力公理二：传递性公理：对于选择集X 中任何的三个要素1x 、2x 和3x ，如果12x x 和23x x ，则有13x x 。

高级微观经济学
高级微观经济学是对微观经济学的更深入、更复杂的研究和分析。

微观经济学研究个体经济主体的决策行为以及个体市场供求关系，而高级微观经济学在此基础上进一步研究了更复杂的市场情况、不完全竞争的市场结构和更精细的经济分析方法。

高级微观经济学的研究内容包括但不限于以下几个方面：
1. 非完全竞争市场：传统微观经济学中的市场是完全竞争的，但实际生活中存在大量的非完全竞争市场，包括寡头垄断、垄断竞争等。

高级微观经济学研究如何在非完全竞争市场下进行更准确的价格理论和政策分析。

2. 市场失灵：高级微观经济学研究市场失灵现象，包括外部性（externalities）、公共物品（public goods）、信息不对称（asymmetric information）等。

这些市场失灵
现象会引起资源配置效率低下，高级微观经济学研究如何解决这些问题。

3. 游戏理论：高级微观经济学中的游戏理论（game theory）是研究经济主体之间互动决策的数学模型。

游戏理论可以应用于各种经济领域，如拍卖、博弈论等，用于分析经济主体如何进行策略选择。

4. 程序经济学：高级微观经济学中的程序经济学（computational economics）使用计算机模拟和数值计算方法来研究经济问题，可以模拟复杂的经济系统和市场交互行为，对于研究经济政策的效果和预测市场行为具有重要意义。

总之，高级微观经济学是对微观经济学更加深入、复杂的研究和分析，涉及非完全竞争市场、市场失灵、游戏理论和程序经济学等领域。

它帮助我们更好地理解和解释经济行为和市场现象，为制定经济政策和进行经济预测提供了更强大的工具和方法。

高级微观经济学-教学大纲(总8页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《高级微观经济学》教学大纲课程编号：031403B课程类型：□通识教育必修课□通识教育选修课□专业必修课✔专业选修课□学科基础课总学时：48 讲课学时：48 实验（上机）学时：0学分：3适用对象：经济学（实验班）先修课程：高等数学、中级微观经济学等一、教学目标《高级微观经济学》旨在进一步培养和提高学生的经济学思维方式、分析能力和对经济学的领悟力，结合中级微观经济学的基础知识，侧重运用数理方法讨论微观经济理论的消费者理论、生产者理论、市场结构与一般均衡的基础模型，熟悉掌握微观经济分析的基本方法与模型，具备阅读经济学专业文献的能力与其他专业课程的必要基础，使学生掌握经济学发展的主流方向和主导前沿。

目标1：理解经济学思维方法目标2：掌握微观经济学分析方法目标3：探索微观经济学发展的主流方向和主导前沿目标4：为其他经济类高级课程铺垫理论基础二、教学内容及其与毕业要求的对应关系教学内容：第一章消费者基本理论、第三章厂商理论、第四章局部均衡和第五章一般均衡应精讲、细讲。

对各章重点内容，教师应阐述清楚基本原理，并在此基础上以一些浅显易懂的案例增进学生的理解，启发学生的求知欲与好奇心；教师应重视基本原理的推导，针对教材内容过于宽泛、难度过大的问题，可针对学生情况有针对性地进行取舍。

教学方法：为实现教学目标，本课程主要采取教师讲授的方式授课，任课教师应以多媒体教学为基本授课方式，也可以采取课堂讨论、案例教学等其他教学手段。

课程要求：任课教师应要求学生在课前预习，课后布置一些较深入的问题供学生探讨，学生须做课后习题。

教学过程中应注意理论与现实相结合。

与毕业要求的对应关系：高级微观经济学是经济类课程中理论性较强的合成，也是提升学生经济学思维的主要课程，为学生将来在政府机构、经济部门、新闻出版行业、公司和企事业单位从事经济工作、管理工作和经济政策研究工作打下坚实基础。