当前位置：文档之家 › 第15章 对策论 (管理运筹学 第三版 课件 共17章 韩伯棠)40页PPT

第15章 对策论 (管理运筹学 第三版 课件 共17章 韩伯棠)40页PPT

  • 格式：ppt
  • 大小：242.00 KB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

决策管理-管理运筹学讲义第15章决策论 精品

决策管理-管理运筹学讲义第15章决策论 精品

（2）理论要点
▪ 管理就是决策 ▪ “管理人”代替“经济人” ▪ 决策满意化与次优化 ▪ 决策是一个过程 ▪ 程序化决策与非程序化决策
2.什么是决策
(1) 什么是决策？
决策就是作决定，领导“拍板”； 从两个以上的备选方案中选择一个的过程就是
决策； 管理者识别并解决问题以及利用机会的过程； 决策，是指组织或个人为了实现某种目标而对
决策科学作为一门学科来讲，仍然处于发展完 善之中，其理论体系正在不断建立完善。但在 社会发展与经济建设中，决策科学已经发挥出 巨大作用。
在我国，改革开放后，国家各级主管部门在指 导经济建设中，大量采用科学的决策方法，科 研院所不断从理论与方法上进行探讨、研究， 各大学也相继开设了决策学等课程，使科学决 策在我国的应用与发展呈现出一派欣欣向荣的 景象。
未来一定时期内有关活动的方向、内容及方式 的选择或调整过程； 决策就是管理，管理就是决策；
（2）决策的概念
决策
决策是一个管理过程，是人们为了实现 特定的目标，运用科学的理论与方法， 系统地分析主客观条件，提出各种预选 方案，从中选出最佳方案，并对最佳方 案进行实施、监控的过程。
决策问题必须具备的三个要素：
在人力、财力、物力等资源方面的准备和组织上所进行的 决策。战术决策属于中期决策，其风险性也属中等。属于 企业的中级层次的决策。 业务决策又称业务控制，是有关日常业务和计划的决策， 其目的是为了提高日常业务工作的效率和经济性，属于基 层决策。
按决策的目标数量划分： 单目标决策 多目标决策 按决策的整体构成划分： 单阶段决策 多阶段决策
对于管理决策来说，特别应提及的安东尼模式和西蒙模式
安东尼模式是把决策分为战略决策，战术决策和业务决策。 战略决策是有全局性的，具有深远影响的决策，其特点是，

运筹学PPT完整版胡运权

运筹学PPT完整版胡运权

C
m n
基可行解：满足变量非负约束条件的基本解，简称基可
行解。
可行基：对应于基可行解的基称为可行基。
可 行 解
非可行解
基解
基可行解
线性规划问题的数学模型
例1.4 求线性规划问题的所有基矩阵。
Page 30
解: 约束方程的系数矩阵为2×5矩阵 r(A)=2，2阶子矩阵有10个，其中基矩阵只有9个，即
运筹学的历史
“运作研究(Operational Research)小组”:解决复 杂的战略和战术问题。例如：
1. 如何合理运用雷达有效地对付德军德空袭 2. 对商船如何进行编队护航，使船队遭受德国潜
艇攻击时损失最少； 3. 在各种情况下如何调整反潜深水炸弹的爆炸深
度，才能增加对德国潜艇的杀伤力等。
Page 4
线性规划问题的数学模型
约束方程的转换：由不等式转换为等式。
aij x j bi
aij x j xni bi
xni 0 称为松弛变量
aij x j bi
aij x j xni bi
xni 0 称为剩余变量
变量 x j 的变0换 可令 xj x，j 显x然j 0
Page 23
用 x3 x3 替换 x3 ，且 x3 , x3 0
线性规划问题的数学模型
Page 25
(2) 第一个约束条件是“≤”号，在“≤”左端加入松驰变量x4， x4≥0,化为等式；
(3) 第二个约束条件是“≥”号，在“≥”左端减去剩余变量x5， x5≥0；
(4) 第3个约束方程右端常数项为-5，方程两边同乘以(-1),将右 端常数项化为正数；
x
v a 2x2 x a dv 0 dx
2(a 2 x) x (2) (a 2 x)2 0

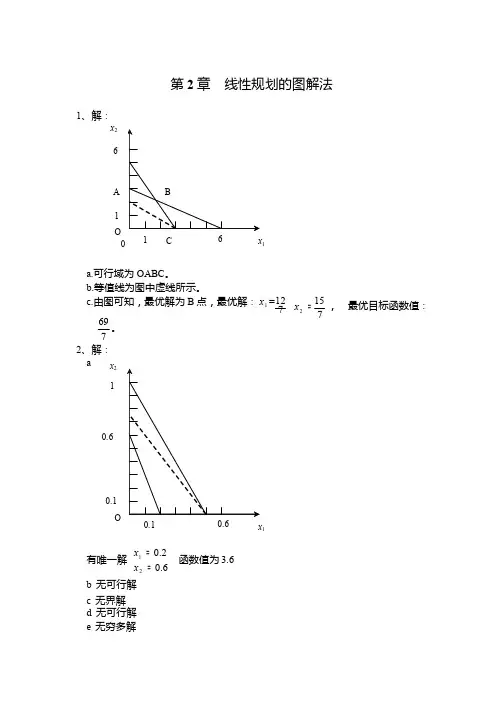
《管理运筹学》第三版习题答案（韩伯棠教授）

《管理运筹学》第三版习题答案（韩伯棠教授）

第 2 章 线性规划的图解法11a.可行域为 OABC 。

b.等值线为图中虚线所示。

12c.由图可知，最优解为 B 点，最优解： x 1 = 769 。

7 2、解：15 x 2 =7， 最优目标函数值：a x 210.60.1O1有唯一解x 1 = 0.2函数值为 3.6x 2 = 0.6b 无可行解c 无界解d 无可行解e 无穷多解1 2 2 1 2f 有唯一解20 x 1 =3 8函数值为 92 33、解：a 标准形式：b 标准形式：c 标准形式：x 2 = 3max fmax f= 3x 1 + 2 x 2 + 0s 1 + 0s 2 + 0s 3 9 x 1 + 2x 2 + s 1 = 303x 1 + 2 x 2 + s 2 = 13 2 x 1 + 2x 2 + s 3 = 9 x 1 , x 2 , s 1 , s 2 , s 3 ≥= −4 x 1 − 6x 3 − 0s 1 − 0s 23x 1 − x 2 − s 1 =6x 1 + 2x 2 + s 2 = 10 7 x 1 − 6 x 2 = 4x 1 , x 2 , s 1 , s 2 ≥max f = −x ' + 2x ' − 2 x ''− 0s − 0s'''− 3x 1 + 5x 2 − 5x 2 + s 1 = 70 2 x ' − 5x ' + 5x '' = 50122' ' ''3x 1 + 2 x 2 − 2x 2 − s 2 = 30'' ''4 、解：x 1 , x 2, x 2, s 1 , s 2 ≥ 0标准形式： max z = 10 x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4 x 2 + s 1 = 9 5x 1 + 2 x 2 + s 2 = 8 x 1 , x 2 , s 1 , s 2 ≥ 0s 1 = 2, s 2 = 0标准形式： min f = 11x 1 + 8x 2 + 0s 1 + 0s 2 + 0s 310 x 1 + 2x 2 − s 1 = 203x 1 + 3x 2 − s 2 = 18 4 x 1 + 9x 2 − s 3 = 36 x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0s 1 = 0, s 2 = 0, s 3 = 136 、解：b 1 ≤c 1 ≤ 3c 2 ≤ c 2 ≤ 6d x 1 = 6 x 2 = 4e x 1 ∈ [4,8]x 2 = 16 − 2x 1f 变化。

韩伯棠教授《管理运筹学》第三版习总复习

韩伯棠教授《管理运筹学》第三版习总复习

一、管理运筹学的定义运筹学（Operational Research，简称OR) ，英文直译为“运作研究”。

管理运筹学是应用分析、试验、量化的方法，对经济管理系统中的人力、物力、财力等资源进行统筹安排，为决策者提供有依据的最优方案，以实现最有效的管理。

——《中国企业管理百科全书》绪论二、管理运筹学Ⅰ的主要分支线性规划(Linear Programming，简称LP)整数规划(Integral Programming，简称IP)目标规划(Objective Programming，简称OP)动态规划(Dynamic Programming，简称DP)图与网络(Graph and Network)三、管理运筹学的工作步骤提出问题、分析问题建立模型求解解的检验、控制、实施四、运筹学方法的特点1. 最优化方法2. 定量的方法线性规划(LP)一、问题的提出1.生产计划安排问题：合理利用人力、物力、财力等，在资源有限的约束条件下,寻求使得获利最大的最优生产计划方案。

2.人力资源分配的问题：在满足工作的需要的条件下，寻求使用最少的劳动力的最优分配方案。

3.套裁下料问题：在保证正常生产，完成生产任务的条件下，寻求使用原料最省的最优下料方案。

4.投资问题：在投资额限制的条件下，从多个投资项目中选取使得投资回报最大的最优投资方案。

5.运输问题：寻求使得总运费最小的最优调运方案。

二、建模1.一般步骤:分析问题，设出决策变量根据所提问题列出目标函数根据已知条件列出所有约束条件数学模型的一般形式★矩阵形式：假设有n个决策变量，m个约束条件。

目标函数：Max （Min） z = CX约束条件：AX ≤（ =, ≥）b.X≥ 0其中，C=(c1 , c2 , … , cn )(价值向量)X= (x1 , x2 , … , xn )T(决策变量向量)b=(b1 , b2 , … , bm )T (限定向量)a11 a12 (1)a21 a22 … a2n (约束条件系数矩阵)Am×n = ……am1 am2 … amn数学模型的特点（1）由目标函数和约束条件构成；（2）目标函数只有两种情况：求极小或求极大。

管理运筹学全套ppt课件

管理运筹学全套ppt课件
线性规划模型
设置变量：生产Ⅰ 产品x1个， Ⅱ产品 x2个
目标函数是利润最大化：
maz x5x 0 110x20
资源是有限的，第一个限制是设备台时 的限制：
x1x2 300
采用PP管及配件：根据给水设计图配置好PP管及配件，用管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
线性规划模型
建模型如下：设生产Ⅰ 产品x1件, Ⅱ产品 x2件。
max z 50 x1 100 x 2 (1)
x1 x 2 300
s
.t
.
2 x
x1 x 2 2 250
400 (2)
x1 , x 2 0
采用PP管及配件：根据给水设计图配置好PP管及配件，用管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
线性规划模型
第二个限制是原材料A的限制： 2x1x2 400
第三个限制是原材料B的限制：
x2 250
显然，产量不可能为负数：
x1,x2 0
采用PP管及配件：根据给水设计图配置好PP管及配件，用管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
采用PP管及配件：根据给水设计图配置好PP管及配件，用管件在 管材垂 直角切 断管材 ，边剪 边旋转 ，以保 证切口 面的圆 度，保 持熔接 部位干 净无污 物
考核方法
平时成绩占20%，每位同学的初始成绩都 是60分（按100分为满分计算）。
每次作业交上加1分，不交不加不减，拷 贝别人作业一次扣2分。
运筹学的体系和发展历史
二次世界大战中，英美科学家研究如何 有效运用雷达，研究船队遇到袭击如何 减少损失，以及如何使用深水炸弹等紧 迫问题。

运筹学-对策论

运筹学-对策论

3.矩阵对策的混合策略
例：设一个赢得矩阵如下:
5 A = 8 max 8 6 9 6 min
j
9
min 5 max
i
6 策略α2
8 策略β1
• 思路：对甲（乙）给出一个选取不同策 略的概率分布，以使甲（乙）在各种情 况下的平均赢得（损失）最多（最少）。 -----即混合策略
重要定理
定理 任一矩阵对策G {S1,S2;A}， 任一矩阵对策G＝{S1,S2;A}，一定存在混 合策略意义下的解。 合策略意义下的解。 • 定理 设有两个矩阵对策 • G1＝ G2＝ G1＝{S1,S2;A1} G2＝{S1,S2;A2} • 其中A1＝(aij)，A2＝(aij+L)，L为任一常数。 A1＝ 其中A1 (aij)，A2＝(aij+L)， 为任一常数。 则 • (1)G1 G2同解 G1与 同解； (1)G1与G2同解； • (2)VG2 VG2＝ (2)VG2＝VG1+L
7.4 矩阵对策的解法
• (1) 2×2矩阵对策的线性方程组法 2× • 所谓2 所谓2×2矩阵对策是指局中人Ⅰ的赢得矩阵为2×2阶的，即 矩阵对策是指局中人Ⅰ的赢得矩阵为2 是指局中人 阶的， A = a11 a12 • a21 a22 • 如果此对策有纯策略意义下的解，则很容易求解； 如果此对策有纯策略意义下的解，则很容易求解；如果没有 纯策略意义下的解， 纯策略意义下的解，则为求出各局中人的最优混合策略可求解下 列方程组： 列方程组： • a11x1＋a21x2＝ a11y1＋a12y2＝ a11x1＋a21x2＝v a11y1＋a12y2＝v • a12x1＋a22x2＝ a21y1＋a22y2＝ a12x1＋a22x2＝v a21y1＋a22y2＝v • y1＋y2＝ x1＋x2＝ y1＋y2＝1 x1＋x2＝1 • 当没有纯策略意义下的解时，方程组一定有严格非负解 x*= 当没有纯策略意义下的解时， x1* x2* y*=（y1*，y2*）， （x1*，x2*）和y*=（y1*，y2*）， 即为各局中人的最优混合策 略。

对策论模型

对策论模型

9 7 y E ( X , Y ) ( x,1 x) 2 8 1 y
=8xy－6y－x+8 3 1 1 8( x )( y ) 7 = 4 8 4
3 1 这就是说，局中人分别以概率 X * ( , ) 选用1,2 时，至少 4 4 1 1 7 * 赢得 7 ，同理，局中人Ⅱ分别以概率Y ( , ) 选用策略1,2， 4 8 8 1 3 1 1 7 7 。但当 X * ( , ) 或 Y * ( , ) 时，则会受到更大的 至多损失 4 4 4 8 8 损失。
1.混合策略和混合局势
一般地, 设给定 S1 , S2 ; A, 令 X ( x1 , x 2 , , x m), Y ( y1 , y2 , , yn )
m m
S {X | x i 0; x i 1}, S {Y | y j 0; y j 1}
1
1 1 3 1
-1
1 1 1 3
A=
1 -1 1 1
-1 1
这是一个两人有限零和对策。
二、在纯策略下有解的矩阵对策的解法
1.解法的思想：双方都立足在不利的情况下争取最好的结果 ──最大最小原则。 例 求解矩阵对策 ={S1,S2;A}，其中:
7 3 A 16 3 1 8 2 4 4 3 0 5
解：
1
1 7 2 3 3 16 4 3
i
2
1
3
min a ij
j
max aij
8 2 4 4 3 0 5 16 2 5
8 2 max ai j 2 i 3 3
*
min aij* 2

运筹学教学-对策论公开课获奖课件百校联赛一等奖课件

运筹学教学-对策论公开课获奖课件百校联赛一等奖课件
局中人称为“i旳对手”，记为-i。
对策中利益一致旳参加者只能看成一种局中人，例：桥牌中 旳东、西两方。 对策论中对局中人旳一种主要假设：每个局中人都是“理智 旳”，即每一种局中人都不存在侥幸心理，不存在利用其他 局中人决策旳失误来扩大本身利益旳行为。
基本概念
在策略型博奕中，一种对策有下列几种基本要素： 一．局中人 二．策略(strategies)：
-1
1
布
1
0
-1
剪刀
-1
1
0
第三节 矩阵对策旳纯策略
例：设有一矩阵对策 G {S1, S2; A} 其中
6 1 8
A
3
2
4
9 1 10
3 0
6
解：对局中人I而言，最大赢得是9，若想得到这个赢得，
他要选择纯策略 ，3因为局中人II也是理智旳竞争 者，他已考虑到局中人I打算出 旳3心理，则准备 以 3对付之，使局中人I不但得不到9，反而失掉10. 局中人I当然也会猜到局中人II旳心理，故而出 4
I {1,2,..., n}
Si ;i 1,2,..., n
局势----状态
n
S Si i 1
支付函数
支付有关局势旳函数----决策根据和原则 H i (s);i 1,2,..., n, s S
模型 I {1,2,..., N }, Si , i I , H i (s), i I
二人：参加对策旳局中人有两个；
有限：局中人旳策略集都为有限集；
零和：在任一局势下，两个局中人旳赢得之和总等于0，即，
一种局中人旳所得值恰好是另一种局中人旳所失值，双方旳 利益是完全对抗旳。
设局中人I和II旳策略集分别为
S1 {1,2 ,...,m } S2 {1, 2 ,..., n}

运筹学全册精品完整课件

运筹学全册精品完整课件
否则，目标函数等值线与可行域 将交于无穷远处，此时称无有限最 优解。
36
例2-2 考虑例2-1
某工厂拥有A、B、C 三种类型的设备，
生产甲、乙两种产品。每件产品在生产中 需要占用的设备机时数，每件产品可以获 得的利润以及三种设备可利用的时数如下 表所示。问题：工厂应如何安排生产可获 得最大的总利润？
一、线性规划问题的提出
在实践中，根据实际问题的要求，常常 可以建立线性规划问题数学模型。
例2-1 我们首先分析开篇案例提到的问题。 解：设变量 xi 为第 i 种（甲、乙）产品的 生产件数（i＝1，2）。根据题意，我们知道 两种产品的生产受到设备能力（机时数）的 限制。对设备A：两种产品生产所占用的机时 数不能超过65，于是我们可以得到不等式：
运筹学是运用科学的方法（如 分析、试验、量化等）来决定如何 最佳地运营和设计各种系统的一门 学科。
4
运筹学概述
运筹学能够对经济管理系统中 的人力、物力、财力等资源进行统 筹安排，为决策者提供有依据的最 优方案，以实现最有效的管理。
通常以最优、最佳等作为决策 目标，避开最劣的方案。
5
运筹学的产生和发展
8பைடு நூலகம்
运筹学在管理中的应用
生产计划：生产作业的计划、日程表的
编排、合理下料、配料问题、物料管 理等。
库存管理：多种物资库存量的管理，库
存方式、库存量等。
运输问题：确定最小成本的运输线路、
物资的调拨、运输工具的调度以及建
厂地址的选择等。
9
运筹学在管理中的应用
• 人事管理：对人员的需求和使用的 预测，确定人员编制、人员合理分 配，建立人才评价体系等。
x1 ，x2 ，… ，xn ≥ 0

运筹学--对策论

运筹学--对策论

max min E(X,Y)= min max E(X,Y)
X S1* Y S2*
Y S2* X S1*
则称这个公共值为对策G在混合意义 下的值，记为V*G，而达到V*G 的混 合局势（X*，Y*）称为对策G在混合 策略意义下的解，而X*和Y*分别称 为局中人I，II的最优混合策略。
定理14-2：矩阵对策 G = S1，S2；A
0 2 3 0
赢得矩阵为 A 2 0 3 0
0
3
0 4
0
3
4
0
14.2 矩阵对策的混合策略
定义:对给定的矩阵对策
G = Ⅰ，Ⅱ；S1,S2;A
其中 S1= 1, 2…m
S2= 1 , 2… n
A=(aij)mn
把纯策略集合对应的概率向量
X=(x1, x2 … xm) 其中 xi 0 xi=1 和 Y=(y1 , y2 … yn ) 其中 yj 0 yj=1
分别称为局中人I和局中人II的混合策略。
如果局中人I选取的策略为
X=(x1, x2 … xm) 局中人II选取的策略为
Y=(y1 , y2 … yn )，则期望值 E（X，Y）= xi aij yj=XAYT 称为局中人I期望赢得，而局势（X，Y） 称为“混合局势”，局中人I，II的混合 策略集合记为S1*， S2*。
S1= 1、 2…… m
同样，局中人II有n个策略：1、 2。。。 n ；用S2表示这些策略的集合： S2= 1、 2… n 局中人I的赢得矩阵是：
a11 a12 …… a1n a21 a22 …… a2n A= …… …… …… a m1 a m2 … a mn
局中人II的赢得矩阵是 -A 把一个对策记为G： G= S1，S2；A

管理运筹学 全套课件

管理运筹学 全套课件
运筹学是一门应用于管理有组织系统的科学，为决策者提供最优方案。文档介绍了运筹学的魅力与实质，通过数学例子展示其思维方式。考核方法部分说明了成绩评定规则。运筹学的体系和发展历史从起源讲起，涵盖其在战争中的应用及现实生活中的例子。学科体系包括规划论、图论与网络分析、排队论、决策论、存储论和博弈论。工作步骤从问题提出到模型建立、求解、检验和实施进行了概述。最后，文档进入第一章线性规划的介绍，详细阐述了线性规划模型，通过生产决策问题的实例，展示了如何建立线性

运筹学答案_第_15_章__对策论

运筹学答案_第_15_章__对策论

α
1
3
分为 12.6582；乙队教练应以 0.6709的概率出策略 β1，以 0.3291 的概率出策略3 ， β
平均得分为 27-12.6582=14.3418。 管理运筹学 2.0 可从损益矩阵直接求得上述问题答案，结果如下图。
对策最优解如下
************************* 局中人甲： X*=(.671,.329)T 局中人乙： Y*=(.671,.329)T
由 1 = x +x +x +x + x + x 得v= 2.5126 v
由x =v⋅ x 可得： x =0.3266,x =0.2739,x ′=0.2186,′x =0,x
i
i
1
2
3
4
′=0.1809,x ′=0
5
6
所以齐王的最优对策是以 0.3266 的概率出 ，以 0.2739 的概率出α ，以 0.2186
3
3α
4
4
α 、β 表示做电视、报纸、广播广告；α 、β 表示做报纸广告；α 、β 表示
5
5
6
6
7
7
做报纸、广播广告；α8 、 β8表示做广播广告。
局中人 A 的损益矩阵为：
β1
ββ ββββ
2
3
4
5
6
7
8
β
α1 50% 25% 10% 15% 0 35% 25% 40%
α2 75% 50% 35% 40% 25% 60% 50% 65%
第 15 章 对策论
1、解：因为
max
i
min
j
a
ij
= min

第15章 对策论 (管理运筹学 第三版 课件 共17章 韩伯棠)40页PPT

第15章 对策论 (管理运筹学 第三版 课件 共17章 韩伯棠)40页PPT
解：局中人I为采购员，局中人II为大自然，采购员有三个策 略，买10吨、15吨、20吨。分别记为1，2，3。大自然也有三个 策略：暖、正常、冷，分别记为1，2，3。
管理运筹学
9
§2 矩阵对策的最优纯策略
赢得矩阵如下：
1
2
3
1(10吨） -100
-175
-300
2(15吨） -150
-150
-250
即 max min aij min max aij 。
ij
ji
一个自然的想法：对甲（乙）给出一个选取不同策略的概率分 布，以使甲（乙）在各种情况下的平均赢得（损失）最多（最少） -----即混合策略。
管理运筹学
12
§3 矩阵对策的混合策略
求解混合策略的问题有图解法、迭代法、线性方程法和线性规 划法等，我们这里只介绍线性规划法，其他方法略。
7
§2 矩阵对策的最优纯策略
矩阵A中每行的最小元素分别为1，-3，-1。
在这些最少赢得中最好的结果是1，故甲队会采取策略1，无论对手 采取何策略，甲队至少得1分。对于乙队，{1，2，3}可能带来的最少 赢得，即A中每列的最大元素，分别为3，1，3。乙队会采取2策略，确保 甲队不会超过1分。
1和2分别称为局中人甲队、乙队的最优策略。由于双方必然选择这 一种策略，所以，这种策略又称为最优纯策略。
支付给局中人甲以数量为此和数的报酬；如果两人所写数字之和为奇数，
则局中人甲付给局中人乙以数量为此和数的报酬。试求出其最优策略。
解：首先计算局中人甲的赢得矩阵如下表：
甲的赢 得
乙的策略 1（出1） 2（出2）
甲的策略
3（出3）
1（出1）
2
-3

运筹与优化对策论PPT课件

运筹与优化对策论PPT课件

是对策G的两个解,则 akr =apq.
事实上,由 aij ,有aij aij
apq≤ apr≤ akr ≤ akq ≤ apq
因此 akr =apq.
6 5
2
1
7 5
6
2
第9页/共44页
性质2(可交换性).若(αk,βr)和 (αp,βq) 是对策G的两个解,则(αk,βq)和 (αp,βr) 也是对策G的解. 由 aiq ≤ apq= akr ≤ akq≤ apq = akr ≤ akj 得aiq≤akq≤ akj ,即akq是鞍点. 故(αk,βq)是解.同理，(αp,βr)是解.
,
y
∈
S
* 2
,
则
(
x
*
,
y
*
)
是
G
的
解
的
充
要
条
件
是
:
对任意i=1,2,…,m
和
j=1,2,…,n,有
E(i,y*)≤E(x*,y*)≤E(x*,j) (7)
证明:设(x*,y*)是G的解,则由定理2,有
E(x,y*)≤E(x*,y*)≤E(x*,y) (4)
由于纯策略是混合策略的特例,故(7)式成立. 反之,设(7)式成立,由(5)、(6)有 E(x,y*)=∑E(i,y*)xi≤E(x*,y*)∑xi=E(x*,y*) E(x*,y)=∑E(x*,j)yj≥E(x*,y*)∑yj=E(x*,y*)可知(4)式成立，故(x*,y*)是G的解
S1={α1,α2,α3,α4}, S2={β1,β2,β3},
6 1 8
A
3
2
4
9 1 10
试求双方的最优策略和赢得.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解：局中人I为采购员，局中人II为大自然，采购员有三个策 略，买10吨、15吨、20吨。分别记为1，2，3。大自然也有三个 策略：暖、正常、冷，分别记为1，2，3。
管理运筹学
9
§2 矩阵对策的最优纯策略
赢得矩阵如下：
1
2
3
1(10吨） -100
-175
-300
2(15吨） -150
-150
-250
管理运筹学
2
§1 对策论的基本概念
“齐王赛马”齐王在各局势中的益损值表（单位：千金）
管理运筹学
3
§1 对策论的基本概念
其中：齐王的策略集: S1={ 1, 2, 3, 4, 5, 6 }， 田忌的策略集：S2={ 1, 2, 3, 4, 5, 6 }。
下面矩阵称齐王的赢得矩阵：
3 1 1 1 -1 1 1 3 1 1 1 -1 A= 1 -1 3 1 1 1 -1 1 1 3 1 1 1 1 1 -1 3 1 1 1 -1 1 1 3
7
§2 矩阵对策的最优纯策略
矩阵A中每行的最小元素分别为1，-3，-1。
在这些最少赢得中最好的结果是1，故甲队会采取策略1，无论对手 采取何策略，甲队至少得1分。对于乙队，{1，2，3}可能带来的最少 赢得，即A中每列的最大元素，分别为3，1，3。乙队会采取2策略，确保 甲队不会超过1分。
1和2分别称为局中人甲队、乙队的最优策略。由于双方必然选择这 一种策略，所以，这种策略又称为最优纯策略。
管理运筹学
4
§1 对策论的基本概念
二人有限零和对策（又称矩阵对策）： 局中人为2；每个局中人的策略集的策略数目都
是有限的；每一局势的对策均有确定的损益值，并 且对同一局势的两个局中人的益损值之和为零。
通常将矩阵对策记为: G = {S1, S2, A} S1：甲的策略集； S2：乙的策略集； A：甲的赢得矩阵。 “齐王赛马”是一个矩阵策略。
11
§3 矩阵对策的混合策略
当甲取策略2 ，乙取策略1时，甲实际赢得8比预期的多2，
乙当然不满意。考虑到甲可能取策略2这一点，乙采取策略2。若 甲也分析到乙可能采取策略2这一点，取策略1，则赢得更多为 9 … 。此时，对两个局中人甲、乙来说，没有一个双方均可接受
的平衡局势，其主要原因是甲和乙没有执行上述原则的共同基础，
min -300 -250 -200*
管理运筹学
10
§3 矩阵对策的混合策略
设矩阵对策 G = { S1, S2, A }。当
max
i
min
j
aij
min
j
max
i
aij
时，不存在最优纯策略。
例：设一个赢得矩阵如下:
min
59 5 A=
86 6
max 6
i
策略2
max 8 9
min 8
j
策略1
管理运筹学
1分，可知三赛三胜得3分，三赛二胜得1分，三赛一胜得-1分，三
赛三负得-3分。甲队的策略集为S1={1，2，3}，乙队的策略集
为S2={1，2，3}。根据以往比赛的资料，有甲队的赢得矩阵为A，
如下所示，
1 1 1 A 1 1 3
3 1 3
请问这次比赛各队采用哪种阵容上场最为稳妥?
管理运筹学
即 max min aij min max aij 。
ij
ji
一个自然的想法：对甲（乙）给出一个选取不同策略的概率分 布，以使甲（乙）在各种情况下的平均赢得（损失）最多（最少） -----即混合策略。
管理运筹学
12
§3 矩阵对策的混合策略
求解混合策略的问题有图解法、迭代法、线性方程法和线性规 划法等，我们这里只介绍线性规划法，其他方法略。
在考虑各方采用的策略时，必须注意一个前提，就是双 方都是理智的，即双方都是从各自可能出现的最不利的情形 选择一种最为有利的情况作为决策的依据。
管理运筹学
6
§2 矩阵对策的最优纯策略
例：甲乙乒乓球队进行团体对抗赛，每队由三名球员组成，双
方都可排成三种不同的阵容，每一种阵容可以看作一种策略，双方
各选一种策略参赛。比赛共赛三局，规定每局胜者得1分，输者得-
3(20吨） -200
-200
-200
在此表上计算，有
1
2
3Байду номын сангаас
1(10吨） -100
-175
-300
2(15吨） -150
-150
-250
3(20吨） -200
-200
-200
max
-100
-150
-200*
得 m i m aj x a ii jn m j m iina ai j xa32 200
故（3，3）为对策G的解，VG=-200。
第十五章 对策论
由“齐王赛马”引入
管理运筹学
1
§1 对策论的基本概念
对策模型的三个基本要素：
1.局中人：参与对抗的各方；
2.策略集：局中人选择对付其它局中人的行动方案 称为策略；某局中人的所有可能策略全体称为策 略集；
3.一局势对策的益损值：局中人各自使用一个对策 就形成了一个局势，一个局势决定了各局中人的 对策结果（量化）称为该局势对策的益损值。
这种最优纯策略只有当赢得矩阵A=（aij）中等式
mi am xj ianijmj im ni aaixj
成立时，双方才有最优纯策略，并把（1,2）称为对策G在纯策略下的解， 又称（1,2）为对策G的鞍点。把其值V称之为对策G={S1，S2，A}的值。
管理运筹学
8
§2 矩阵对策的最优纯策略
例 某单位采购员在秋天决定冬季取暖用煤的储量问题，已知 在正常的冬季气温条件下要消耗15吨煤，在较暖和较冷的天气下要 消耗10吨和20吨。假定冬天的煤价随天气寒冷程度而有所变化，在 较暖和、正常、较冷的气候条件下每吨煤价分别为10元、15元、20 元。又设冬季时煤炭价格为每吨10元。在没有关于当年冬季准确的 气象预报的条件下，秋天储煤多少吨能使得单位的支出最少？
管理运筹学
5
§§22 矩矩阵阵对对策策的的最最优优纯纯策策略略
在甲方的赢得矩阵中：
A=[aij]m×n i 行代表甲方策略 i=1, 2, …, m；j 行代表乙方策略 j=1, 2, …, n；aij 代表甲方取策略 i，乙方取策略 j，这一局势下甲方的 益损值。此时乙方的益损值为 -aij（零和性质）。
例：设甲使用策略1的概率为X1′，使用策略2的概率为X2′ ， 并设在最坏的情况下，甲赢得的平均值为V（未知）。
59
A= 86
STEP 1 1) X1′+X2′=1
X1′, X2′0
管理运筹学
13
§3 矩阵对策的混合策略
2)无论乙取何策略，甲的平均赢得应不少于V: