5-7 电磁场的动量

电磁场与电磁波电子教案第一章：电磁场的基本概念1.1 电磁场的定义与特性1.2 电磁场的基本方程1.3 电磁场的边界条件1.4 电磁场的能量与辐射第二章：静电场2.1 静电场的基本方程2.2 静电场的边界条件2.3 静电场的能量与能量密度2.4 静电场的势与电场强度第三章：稳恒磁场3.1 稳恒磁场的性质3.2 稳恒磁场的磁感应强度3.3 磁场的基本方程3.4 磁场的边界条件第四章：电磁波的基本概念4.1 电磁波的产生与传播4.2 电磁波的波动方程4.3 电磁波的能量与动量4.4 电磁波的极化与反射、折射第五章：电磁波的传播与应用5.1 电磁波在自由空间的传播5.2 电磁波在介质中的传播5.3 电磁波的辐射与天线理论5.4 电磁波的应用（如无线通信、微波炉等）第六章：电磁波的波动方程与群速度6.1 电磁波的波动方程6.2 电磁波的相速度与群速度6.3 电磁波的色散现象6.4 电磁波的传播特性分析第七章：电磁波的极化与散射7.1 电磁波的极化类型与极化率7.2 电磁波的圆极化与线极化7.3 电磁波的散射现象及其原理7.4 电磁波散射的应用（如雷达、遥感等）第八章：电磁波在天线理论与辐射中的应用8.1 天线的基本原理与类型8.2 天线的辐射特性与方向性8.3 天线的设计与优化8.4 电磁波在天线辐射中的应用（如无线通信、广播等）第九章：电磁波在介质中的传播与波导9.1 电磁波在均匀介质中的传播9.2 电磁波在非均匀介质中的传播9.3 波导的基本概念与特性9.4 波导中的电磁波传播与应用第十章：电磁波在现代科技领域的应用10.1 无线通信与电磁波10.2 微波炉与电磁波10.3 雷达技术与电磁波10.4 光学与电磁波（如光纤通信、激光等）10.5 电磁波在其他领域的应用（如医学、工业等）重点和难点解析重点一：电磁场的基本概念补充说明：电磁场的定义是电荷产生的一种场，具有能量和动量。

基本方程包括高斯定律、法拉第感应定律和安培定律。

带电粒子在磁场中的运动与动量有关。

在匀强磁场中，如果粒子所受合外力为零，则粒子作匀速直线运动；合外力充当向心力时，粒子作匀速圆周运动；其余情况，粒子作的是一般的变速曲线运动。

同时，带电粒子在磁场中的运动也与速度有关，速度方向与磁场方向平行时不受洛伦兹力作用，速度方向与磁场方向垂直时洛伦兹力充当向心力。

此外，带电粒子在磁场中的运动还具有周期性，其周期T=2πm/qB或者T=2πr/v，其中m为动量，q为电量，B为磁感应强度。

在处理带电粒子在磁场中的运动问题时，可以采用力的观点（牛顿运动定律、运动学公式）、能量观点（动能定理、能量守恒定律）和动量观点（动量定理、动量守恒定律）等多种方法进行分析。

以上内容仅供参考，如需更全面准确的信息，可查阅物理专业书籍或咨询物理专业人士。

电磁场动量介绍电磁场动量是指电磁场传递的动量。

在电磁学中，电磁场由电场和磁场组成，它们在空间中以波的形式传播。

正如我们所熟知的，电磁波可以携带能量，而能量与动量是有关联的。

因此，电磁波也具有动量。

研究电磁场动量可以帮助我们更好地理解电磁波的传播和相互作用。

电磁场动量的数学表达式电磁场动量的数学表达式可以由麦克斯韦方程组推导得到。

在自然单位制下，麦克斯韦方程组可以写成如下形式：1.Maxwell方程组：∇⋅E⃗=ρϵ0∇⋅B⃗ =0∇×E⃗=−∂B⃗ ∂t∇×B⃗ =μ0J+μ0ϵ0∂E⃗∂t其中，E⃗是电场强度，B⃗ 是磁感应强度，ρ是电荷密度，J是电流密度，ϵ0是真空电容率，μ0是真空磁导率。

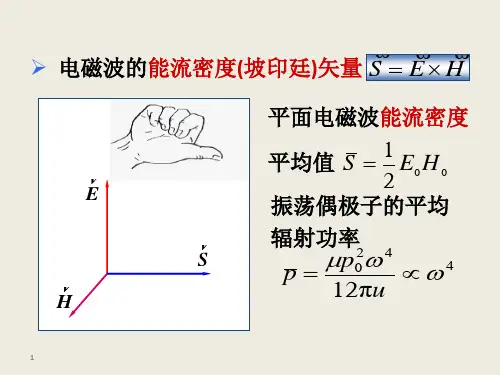
2.电磁场动量密度：g=ϵ0(E⃗×B⃗ )电磁场动量的密度g与电场强度E⃗和磁感应强度B⃗ 的叉乘有关。

通过对麦克斯韦方程组的求解，可以得到电磁场动量的传播速度等信息。

电磁波的动量电磁波是一种特殊的电磁场，它在空间中以波的形式传播，具有能量和动量。

根据电磁场动量的表达式，电磁波的密度流量也可以表示为：S=g⋅c其中，S是电磁波的密度流量，c是光速。

这意味着，电磁波在空间中传播时，具有一个方向和大小都固定的动量密度。

电磁场动量的应用电磁场动量在许多领域具有重要的应用。

以下是一些常见的应用领域：1. 光压效应光压效应是指光对物体施加的压力。

当光照射到物体表面上时，光的动量就会传递给物体表面的粒子，从而产生压力。

这种压力作用可以用电磁场动量的概念来解释和计算。

2. 天体物理学中的电磁辐射在天体物理学中，电磁场动量的概念对于解释和理解天体物体之间的相互作用非常重要。

例如，恒星的辐射压力是由于恒星内部产生的电磁辐射对恒星表面施加的压力所导致的。

3. 激光加速器激光加速器利用激光束对微粒或细胞进行加速。

激光束的动量可以传递给微粒或细胞，使其加速。

这种加速器的原理和操作都基于电磁场动量的概念。

电磁场的角动量一、引言电磁场的角动量是指电磁场固有的自旋角动量和由电荷在电磁场中运动所带来的轨道角动量。

它是电磁学中一个非常重要的概念，对于理解电磁学基本原理和应用具有重要意义。

二、自旋角动量1. 自旋角动量的概念自旋是指物体固有的旋转运动，这种运动产生了一个固有的角动量，称为自旋角动量。

在电磁学中，光子、波色子等粒子都具有自旋。

自旋角动量可以用一个叫做“自旋量子数”的整数或半整数来描述。

2. 自旋与磁矩由于带电粒子具有固有的自旋，因此它们也会产生一个固有的磁矩。

这个磁矩可以通过朗德因子来计算。

3. 自旋与轨道耦合当带电粒子在外部电场或者磁场中运动时，其自身的自旋和轨道运动会发生相互作用，形成一个称为“轨道-自旋耦合”的效应。

三、轨道角动量1. 轨道角动量的概念电荷在电磁场中运动时，会产生一个围绕其运动轨迹的角动量，称为轨道角动量。

轨道角动量大小与电荷的运动速度和运动轨迹有关。

2. 磁矩与轨道角动量由于带电粒子具有固有的轨道角动量，因此它们也会产生一个固有的磁矩。

这个磁矩可以通过朗德因子来计算。

3. 轨道角动量与自旋耦合当带电粒子在外部电场或者磁场中运动时，其自身的自旋和轨道运动会发生相互作用，形成一个称为“轨道-自旋耦合”的效应。

四、总角动量1. 总角动量的概念总角动量是指由自旋和轨道角动量组成的总体积。

在某些情况下，自旋和轨道角动量可以分别看作是相对独立的两个部分，在这种情况下，总角动量等于它们之间的简单相加。

2. 总角动量大小与方向总角动量大小可以通过各种物理实验来测定。

其方向则由自旋和轨道角动量的方向决定。

3. 总角动量守恒总角动量在物理学中具有守恒性质，即在一个系统内部，总角动量的大小和方向不会发生改变。

五、结论电磁场的角动量是指电磁场固有的自旋角动量和由电荷在电磁场中运动所带来的轨道角动量。

自旋和轨道运动之间存在耦合效应。

总角动量是由自旋和轨道角动量组成的总体积，其大小可以通过各种物理实验来测定。

电磁场中粒子的运动规律是经典电动力学研究的重要课题。

当一个粒子在电磁场中运动时，其受到的力是由电场力和磁场力共同作用的。

电磁场的作用力不仅会改变粒子的速度和方向，也会影响粒子的跃迁和旋转，从而影响其物理性质。

一、电场力与磁场力的作用电磁场是由电场和磁场组成的，其中电场的作用是使带电粒子具有电势能，而磁场则是使带电粒子受到洛伦兹力的作用。

电场力和磁场力的作用方式不同：当粒子带电荷并静止的时候，它就处于电场中，受到的力就是电场力；而当粒子在移动过程中，除了受到电场力的作用外，还会受到一种称为洛伦兹力的磁场作用力。

二、带电粒子在电场中的运动当粒子在电场中运动时，电场会使其具有电势能。

根据电场力的方向，粒子的运动方向会受到影响，电场力的作用会导致粒子具有加速度。

如果粒子的速度和电场方向相同，那么受力方向则不会改变，其运动状态将会保持不变。

如果粒子的速度和电场方向相反，那么这个粒子会被反向加速，直到速度和加速度方向相同，引力变成摩擦力之后才会逐渐静止。

三、带电粒子在磁场中的运动当粒子在磁场中运动时，其速度会受到磁场力的作用，并且会跟随着一个螺旋轨迹。

在电磁场的作用下，一个带电粒子在磁场中的运动路径是呈螺旋线的，而且带电粒子的运动方向和磁场的方向都会对粒子的螺旋轨迹产生影响。

由于洛伦兹力的作用，粒子在一个平面上形成的螺旋轨迹叫做在磁场作用下的霍尔效应。

四、电磁场对粒子的影响电磁场的作用不仅仅只影响着带电粒子的理论模型，还会改变粒子原有的物理性质，例如其动量，能量和自旋，甚至可以通过电子的旋转轨道对化学反应产生影响。

因此，研究电磁场以及粒子在其中的行为是非常重要的。

对于电磁场中的电子来说，如何将电子带电，如何在对不同磁场的作用下产生霍尔效应等都是我们所关心的问题。

这些不仅是理论模型的研究，也有着广泛的应用，例如在材料电学方面，应用此类知识可以研究材料的电性能，以及材料在外界电磁场的作用下的电学特性变化等。

综上所述，电磁场中的粒子运动规律是电动力学研究的重点之一。

动量的通俗理解动量是物理学中一个重要的概念，它可以描述物体在移动时所受力量的大小和方向。

在现代物理学中，它包括物质和能量在内的系统的总量。

本文将介绍动量的通俗理解，以方便人们了解这一重要的概念。

首先，动量的定义是“物体受到的力量与其移动速度的乘积”。

这是一个比较简单的定义，但却能够清晰地表明了动量的意义。

举个例子来说，可以想象一个小车运行在桌面上，如果要想让它移动，肯定需要施加一定的力量，而这个力量就是动量。

其次，动量可以分为动量和动能。

动量是物体受力时受到的力量大小和方向，也就是物体受力时会发生的动作；而动能是物体受力时产生的能量。

换句话说，动量代表了物体的运动行为，而动能则代表了物体的动力。

比如，在小车移动时，可以想象它会受到一定的动量，而且还会有一定的动能，这些动能可以让小车继续移动。

再次，动量也可以分为线性动量和角动量。

线性动量是指物体移动时在某一方向上所具有的动量，而角动量则是指物体移动时在某一轴上所具有的动量。

例如，在上文的小车示例中，当它运行时，它会在直线上具有线性动量，而在侧面上也会具有角动量。

最后，动量的概念也可以运用到物理学的其他领域。

比如，在热力学中，动量可以表示系统内物质和能量的总量。

而在电磁学中，动量也可以表示电磁场的能量，这些能量可以在不同的地方互相作用，最终形成一个动态的电磁场。

总之，从上文所提供的信息可以看出，动量是一个重要的物理概念，它可以用来描述物体运动时受到的力量大小和方向，以及物质和能量在物理学中的总量。

而且，它还可以用来表示物体在移动过程中产生的线性和角动量，以及电磁场的能量。

这也表明，动量既是一个复杂的概念，也是一个十分重要的概念，它可以帮助我们了解物体的运动特性，从而让我们更好地控制物体的运动。

巧用动量定理解决电磁场中粒子复杂运动的问题王汉权(江苏省锡山高级中学ꎬ江苏无锡２１４１７４)摘㊀要:中学生在遇到电磁场中粒子运动问题时ꎬ一般采用画粒子轨迹㊁寻求几何关系的方法并结合有关力㊁能规律进行解题ꎬ但由于 双新 背景下试题经常会设置成多个交替电场㊁磁场的组合场或电磁场㊁重力场的叠加场情境ꎬ粒子运动就变得非常复杂ꎬ不太容易画轨迹找关系.这时如果能注意关注到粒子洛伦兹力ｆ与时间ｔ的累加效果(冲量Ｉｆ)和始末状态的速度变化(动量变化ΔＰ)ꎬ利用动量定理就可以使这类复杂问题迎刃而解.关键词:电场ꎻ磁场ꎻ动量定理ꎻ动力学观点ꎻ能量观点中图分类号:Ｇ６３２㊀㊀㊀文献标识码:Ａ㊀㊀㊀文章编号:１００８－０３３３(２０２３)３１－００９８－０４收稿日期:２０２３－０８－０５作者简介:王汉权(１９６６－)ꎬ男ꎬ江苏省盐城人ꎬ本科ꎬ中学正高级教师ꎬ特级教师ꎬ从事高中物理教学研究.基金项目:本文系江苏省中小学教学研究第十三期立项课题 基于核心素养的物理仿真实验与高中物理教学整合的实践研究 (编号:２０１９ＪＫ１３－Ｌ０３６)的中期性研究成果㊀㊀在处理电磁场中粒子运动时ꎬ学生一般都会采用描绘轨迹㊁寻求几何关系或利用洛伦兹力不做功的特点结合动能定理解题ꎬ但有时会遇到粒子在若干电场㊁磁场交替的组合场或叠加场的物理情境ꎬ运动情况非常复杂ꎬ轨迹也很难直观去描绘ꎬ动能定理有时也会相形见绌.这时候ꎬ如果注意到粒子两个方向速度变化引起的洛伦兹力的冲量Ｉｘ＝ðＢｖｙｑ Δｔ＝ðＢｑΔｙ和Ｉｙ＝ðＢｖｘｑ Δｔ＝ðＢｑΔｘꎬ再结合粒子运动过程始末状态的动量变化ꎬ就可以利用动量定理轻松突破因轨迹难描绘㊁过程难分析等解题瓶颈ꎬ从空间和时间两个维度上完美解决粒子复杂运动的问题.１典型案例研究例１㊀在如图１所示的ｘＯｙ空间中有两段连续的磁感应强度分别为Ｂ１和Ｂ２的匀强磁场(Ｂ１＝２Ｂ２)ꎬ磁感应强度方向均垂直纸面向里ꎬ两段匀强磁场宽度分别为ｄ１和ｄ２(ｄ１＝ｄ２)ꎬ现有一质量为ｍ㊁带电为＋ｑ的粒子从坐标原点Ｏ沿ｘ正方向以速度ｖ０射入磁场Ｂ１ꎬ求粒子离开磁场Ｂ２时速度与水平方向偏角θ２的正弦值.图１㊀例１图１.１模型建构剖析结合审题和粒子大致运动轨迹的描绘ꎬ自然会从试题情境中建构出如图２㊁３所示的物理模型ꎬ在磁场Ｂ１中得到几何关系为Ｒ１ｓｉｎθ１＝ｄ１ꎬ在磁场Ｂ２中的几何关系为Ｒ２ｓｉｎθ２－Ｒ２ｓｉｎθ１＝ｄ２(若磁场Ｂ２后还存在磁场Ｂ３ Ｂｎꎬ同样可推理出Ｒ３ｓｉｎθ３－８９Ｒ３ｓｉｎθ２＝ｄ３ Ｒｎｓｉｎθｎ－Ｒｎｓｉｎθｎ－１＝ｄｎ数学关系ꎬ后面例３中会涉及).由Ｂｖｑ＝ｍｖ２Ｒ得到Ｒ＝ｍｖＢｑꎬ所以Ｒ２＝２Ｒ１ꎬ最后解得ｓｉｎθ２＝３Ｂｑｄｍｖ０.图２㊀模型１示意图㊀㊀㊀㊀图３㊀模型２示意图１.２思路变换求新解题中采用了较为常规的画轨迹找关系的思路ꎬ所以解题着重在寻找前后磁场间的半径Ｒ与偏角θ间的数学关系.如果我们不单注意洛伦兹力提供向心力的动力特征和洛伦兹力不做功的能量特征外ꎬ再深层次分析洛伦兹力ｆ作用的冲量Ｉｆꎬ由于粒子速度方向不断变化ꎬ因此粒子所受洛伦兹力ｆ的冲量并不为零!ｘ方向上:洛伦兹力冲量Ｉｆｘ是由Ｂｖｙｑ引起ꎬ即－ðＢｖｙｑ Δｔ＝ｍ(ｖｘ－ｖ０)①ｙ方向上:洛伦兹力冲量Ｉｆｙ是由Ｂｖｘｑ引起ꎬ即ðＢｖｘｑ Δｔ＝ｍｖｙ－０②利用②式可得到ðＢｖｘｑ Δｔ＝Ｂ１ｄ１ｑ＋Ｂ２ｄ２ｑ＝ｍｖｙ－０ꎬ解得粒子射出磁场时在竖直方向的速度ｖｙ＝３Ｂｑｄｍꎬ求得ｓｉｎθ２＝ｖｙｖ０＝３Ｂｑｄｍｖ０.１.３方法总结体悟利用动量定理来处理粒子复杂运动的问题ꎬ可以省去复杂轨迹不易描绘㊁几何关系不易寻找㊁运动过程较难细致分析的麻烦ꎬ巧妙利用某一方向(如ｘ方向)上位移ｘ的累加ＢｑðΔｘ或磁场Ｂ㊁位移ｘ的累加ｑðＢΔｘꎬ与相垂直的方向(ｙ方向)上动量变化ｍ(Δｖｙ)间构建了相互关联ꎬ充分表现出动量定理在此类问题中的解题优势.例２㊀(２００８高考江苏卷)在ｘｏｙ坐标系中有一场强为Ｂ的水平匀强磁场ꎬ质量ｍ㊁带电＋ｑ的小球从原点Ｏ静止释放ꎬ小球运动轨迹曲线如图４所示.已知此曲线在最低点时曲率半径为该点到ｘ轴距离的２倍ꎬ重力加速度取ｇ.求:图４㊀例２图(１)问略ꎻ(２)小球在运动过程中第一次下降的最大距离ｙＭ.解法１㊀(高考卷标准解答):略解法２㊀(运动合成分解法):利用Ｂｖｘｑ＝ｍｇ得到ｖｘ＝ｍｇＢｑ③可以把小球复杂运动等效成一个是以ｖｘ＝ｍｇＢｑ向右的匀速直线运动㊁一个是从原点Ｏ以速度大小为ｖｘ＝ｍｇＢｑ和方向向左在磁场中逆时针的匀速圆周运动[１]ꎬ因此最低点的最大距离为ｙｍ＝２ｒ＝２ｍｖｘＢｑ＝２ｍ２ｇＢ２ｑ２④解法３㊀(动量定理法):粒子运动到最低点时ꎬ重力做功最多ꎬ所以速度最大ｖＭ且水平向右.之所以水平方向上速度从０变为ｖＭꎬ其实是粒子水平方向洛伦兹力ｆｘ与时间ｔ累积的结果ꎬ利用动量定理ðＢｖｙｑ Δｔ＝ｍ(ｖｍ－０)[２]ꎬ而ðＢｖｙｑ Δｔ＝Ｂｑｙｍꎬ所以Ｂｑｙｍ＝ｍｖｍ－０⑤再根据ｍｇｙｍ＝１２ｍｖ２ｍ联立解得ｙｍ＝２ｍ２ｇｑ２Ｂ２综合上述的三种不同解法ꎬ足可以看出当运动过程比较复杂时ꎬ动量定理解题不需要在过程细节上花费过多精力ꎬ但也需要有明确的审题导向:(１)过程多变复杂㊁几何关系不容易寻找ꎻ(２)某一个方向上出现清晰的速度变化ꎻ(３)对９９应另一个垂直方向上的位移累积量或磁场Ｂ和位移的累积量清晰呈现ꎬ这时候就可以优先考虑选择动量定理来处理.此解法方向明确㊁方便快捷ꎬ同时又能避免题中 已知此曲线在最低点的曲率半径为该点到ｘ轴距离的２倍 多余条件和 曲率半径 等多余概念的干扰.２规律迁移运用２.１粒子在若干连续电场㊁磁场组合场中复杂运动的处理例３㊀(２０１５天津高考卷改编)如图５所示ꎬ在坐标原点Ｏ处有一粒子源ꎬ以相同初速度ｖ０向场区各方向发射质量为ｍ㊁电量为＋ｑ的粒子ꎬ在ｘ>０区域内存在ｎ组相邻的匀强电场Ｅ和匀强磁场Ｂꎬ电场强度Ｅ＝３ｍｖ２０２ｑｄꎬ宽度为ｄꎬ方向水平向右ꎻ磁感应强度Ｂ＝３ｍｖ０ｑｄꎬ方向垂直纸面向里ꎬ不计重力及粒子间的相互作用力.图５㊀例３图(１)(２)问(略).(３)保持该组合场条件不变ꎬ撤去粒子源ꎬ将另一带电粒子从Ｏ点静止释放ꎬ若该带电粒子恰好不能穿过第ｎ组磁场的右边界ꎬ求其比荷ｑᶄｍᶄ.解法１㊀(常规寻求关系):略解法２㊀(动量定理法):粒子在第ｎ层磁场恰好不能穿出ꎬ此时速度与边界相切且方向向上ꎬ设速度为ｖｙｎꎬ在第ｎ组磁场中圆周运动的半径为ｒｎ(下标表示粒子所在组数)ꎬ根据动能定理得ｎｑᶄＥｄ＝１２ｍᶄｖ２ｙｎ－０⑥再分析ｘ㊁ｙ两个方向的运动ꎬ电场方向始终沿水平方向ꎬ并不能改变粒子在ｙ方向的速度(动量)ꎬ则从静止释放至恰好与第ｎ组磁场边界相切ꎬ在ｙ方向上应用动量定理得ðＢｖｘｑᶄ Δｔ＝Ｂｑᶄ ｎｄ＝ｍᶄｖｙｎ－０⑦联立⑥⑦式得到ｑᶄｍᶄ＝１３ｎ ｑｍ.实际解题中发现有部分学生把上述交替组合场等效成连续ｎ个电场Ｅ㊁连续ｎ个磁场Ｂ的组合ꎬ利用ｎｑᶄＥｄ＝１２ｍᶄｖ２ｙｎ㊁Ｂｖｎｑᶄ＝ｍᶄｖ２ｎｒｎ和ｒｎ＝ｎｄ很快得到结果ｑᶄｍᶄ＝１３ｎ ｑｍ.能否可以进行这样的等效处理?我们利用仿真实验软件选择了３电３磁的组合形式进行探究ꎬ实验结果如图６(ａ)(ｂ)所示ꎬ发现粒子的两种运动过程并不相同ꎬ包括粒子运动时间及离开磁场时偏离ｙ的距离也不相同ꎬ但粒子最终离开场时的水平速度ｖｘ和竖直速度ｖｙ却是完全一样的!所以我们不建议采用此简单等效的方法处理问题ꎬ但同时使我们的认识更清晰:粒子在ｙ方向上速度变化与电场力作用无关ꎬ完全取决于水平方向上的ｑðＢΔｘ累加效果ꎬ这也充分验证了应用动量定理解决此类问题的可行性和科学性.图６２.２粒子在电场㊁磁场等叠加场中复杂运动的处理例４㊀(２０１３福建高考卷)如图７(ａ)所示ꎬ空间存在一范围足够大的垂直于ｘＯｙ平面向外的匀强磁场ꎬ磁感应强度大小为Ｂ.让质量为ｍ㊁电荷量为ｑ(ｑ>０)的带电粒子从坐标原点Ｏ沿ｘＯｙ平面以不同的初速度大小和方向入射到该磁场中.不计重力和粒子间的影响.(１)(２)问略.(３)如图７(ｂ)所示ꎬ００１若在此空间再加入沿ｙ轴正向㊁大小为Ｅ的匀强电场ꎬ一粒子从Ｏ点以初速度ｖ０沿ｙ轴正方向发射.研究表明:粒子在ｘＯｙ平面内做周期性运动ꎬ且在任一时刻粒子速度的ｘ分量ｖｘ与其所在位置的ｙ坐标成正比ꎬ比例系数与场强大小Ｅ无关.求该粒子运动过程中的最大速度值ｖＭ[３].图７㊀例４图解法１㊀(高考卷标准解答):结合轨迹可知ꎬ粒子运动到Ｄ点时沿电场方向位移ｙＭ最大ꎬ速度最大且沿水平方向ꎬ有Ｅｑｙｍ＝１２ｍｖ２Ｄｍ－１２ｍｖ２０⑧再由题中 任一时刻ꎬ粒子速度的ｘ分量ｖｘ与其所在位置的ｙ坐标成正比ꎬ比例系数与场强大小Ｅ无关 已知条件ꎬ可以选择Ｅ＝０的特殊情形ꎬ原来复杂曲线就变成一个标准的圆周ꎬ此时ｖｘ＝ｖ０ꎬｙＭ＝Ｒ０ꎬ所以ｖ０＝ｋＲ０ꎬ利用Ｂｖ０ｑ＝ｍｖ２０Ｒ０解得ｋ＝Ｂｑｍ⑨这样在Ｄ点有ｖＤｍ＝ｋｙｍ＝Ｂｑｙｍｍ代入⑧式解出得ｖＤｍ＝ＥＢ＋(ＥＢ)２＋ｖ２０⑩该解法比较常规ꎬ但寻求关系不容易ꎬ运算也较烦琐.解法２㊀(动量定理解题):粒子从Ｏ点运动到Ｄ点ꎬ水平方向速度从０变为ｖＤｍꎬ此速度变化是由粒子洛伦兹力Ｂｖｙｑ与时间ｔ累积引起ꎬ由动量定理得ðＢｖｙｑ Δｔ＝Ｂｑｙｍ＝ｍ(ｖＤｍ－０)再结合Ｅｑｙｍ＝１２ｍｖ２Ｄｍ－１２ｍｖ２０就轻松解得最大速度为ｖＤｍ＝ＥＢ＋(ＥＢ)２＋ｖ２０.这种处理显得思路清晰ꎬ且容易理解和接受ꎬ也同样能克服题中若干多余条件的不良干扰.从案例剖析到解法变换ꎬ可以看到处理粒子复杂运动的问题有多种解题方法ꎬ但不管选用哪种解法ꎬ也不管试题设置情境或所给条件发生什么样的新颖变化ꎬ解题中一定要养成认真分析粒子受力和过程变化的良好习惯ꎬ还要重视一些关键信息的审题(如水平速度㊁最大速度㊁曲率半径㊁恰好离开磁场等)ꎬ然后就可以尝试采用动力学或能量的观点进行解题.当然如果发现仍然无法求解或解题过于复杂㊁繁琐等情况时ꎬ就应当快速定位选用动量的观点来解题.最后要说明一点是动量定理是反映合外力冲量与物体动量变化的规律ꎬ因此使用动量定理时一定要构建物体所受的合力冲量和对应过程的动量变化的关联ꎬ如在例３中ꎬ之所以轻松地用ðＢｖｘｑ Δｔ＝ｍΔｖｙ求解ｙ方向上速度变化ꎬ是因为粒子在ｙ方向上仅存在由ｖｘ引起的洛伦兹力ｆｙꎬ但如果确实需要研究ｘ方向上的运动情况ꎬ则需要加上电场力的冲量ꎬ建立ð(Ｅｑ－Ｂｖｙｑ) Δｔ＝ｍΔｖｘ的方程ꎬ化简得到Ｅｑ ｔ－Ｂｑ(ｙ１＋ｙ２＋ )＝ｍ(０－ｖ０)ꎬ倒是可以求解出粒子在电场中总时间ｔ或粒子在所有磁场中运动ｙ的累加量.参考文献:[１]李雪梅.运用 运动合成与分解思想 巧解复杂曲线运动问题[Ｊ].湖南中学物理ꎬ２０２１(０５):８１－８２.[２]王佑璋.动量定理巧解恒力和洛伦兹力共同作用下的运动问题[Ｊ].数理化解题研究ꎬ２０１７(２８):４６－４７.[３]林贵.用一把 钥匙 速解粒子复杂运动的问题[Ｊ].高中数理化ꎬ２０１３(２３):３２－３３.[责任编辑:李㊀璟]１０１。