人教版八年级数学上乘法公式应用举例
- 格式:doc
- 大小:162.00 KB
- 文档页数:4

八年级上册数学乘法公式一、乘法公式的基本内容。
(一)平方差公式。
1. 公式内容。
- (a + b)(a - b)=a^2-b^2。
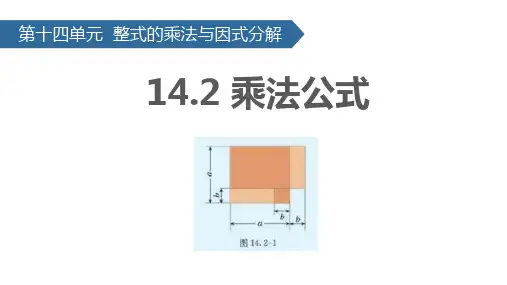
2. 公式的几何解释(以人教版教材为例)- 我们可以通过一个边长为a的大正方形,在其中一角去掉一个边长为b的小正方形来理解。
- 大正方形的面积是a^2,小正方形的面积是b^2。
- 剩下的图形可以看作是一个长为(a + b),宽为(a - b)的长方形,其面积为(a +b)(a - b),所以(a + b)(a - b)=a^2-b^2。
3. 公式的应用示例。
- 例1:计算(3x+2y)(3x - 2y)。
- 解:这里a = 3x,b=2y,根据平方差公式(a + b)(a - b)=a^2-b^2,可得(3x+2y)(3x - 2y)=(3x)^2-(2y)^2=9x^2-4y^2。
- 例2:计算( - 5m+4n)( - 5m - 4n)。
- 解:a=-5m,b = 4n,则( - 5m+4n)( - 5m - 4n)=(-5m)^2-(4n)^2=25m^2-16n^2。
(二)完全平方公式。
1. 公式内容。
- (a + b)^2=a^2+2ab + b^2;(a - b)^2=a^2-2ab + b^2。
2. 公式的几何解释(人教版)- 对于(a + b)^2,可以看作边长为(a + b)的正方形的面积。
- 这个正方形的面积可以分成四部分:边长为a的正方形面积a^2,两个长为a宽为b的长方形面积2ab,边长为b的正方形面积b^2,所以(a + b)^2=a^2+2ab +b^2。
- 对于(a - b)^2,可以看作边长为a的正方形去掉两个长为a宽为b的长方形(这两个长方形有一个边长为b的公共部分)后再加上边长为b的正方形的面积,即(a - b)^2=a^2-2ab + b^2。
3. 公式的应用示例。
- 例1:计算(2x+3y)^2。
- 解:这里a = 2x,b = 3y,根据(a + b)^2=a^2+2ab + b^2,可得(2x+3y)^2=(2x)^2+2×(2x)×(3y)+(3y)^2=4x^2+12xy + 9y^2。



讲 义(a+b)(a-b)=a 2-b 2 (a+b)2=a 2+2ab+b 2 (a-b)2=a 2-2ab+b 2 归纳小结公式的变式,准确灵活运用公式:① 位置变化,(x +y )(-y +x )=x 2-y 2② 符号变化,(-x +y )(-x -y )=(-x )2-y 2= x 2-y 2 ③ 指数变化,(x 2+y 2)(x 2-y 2)=x 4-y 4④ 系数变化,(2a +b )(2a -b )=4a 2-b 2 ⑤ 换式变化,[xy +(z +m )][xy -(z +m )]=(xy )2-(z +m )2=x 2y 2-(z +m )(z +m )=x 2y 2-(z 2+zm +zm +m 2)=x 2y 2-z 2-2zm -m 2⑥ 连用公式变化,(x +y )(x -y )(x 2+y 2)=(x 2-y 2)(x 2+y 2)=x 4-y 4 1、计算下列各式:(1)[(x +y)3]4 ; (2) (a 4n )n -1 ;(3) (-a 3)2+(-a 2)3-(-a 2)·(-a)4 ;(4) x 3·x 2·x 4+(-x 4)2+4(-x 2)4例. 计算:()()53532222x y x y +-(二)、连用:连续使用同一公式或连用两个以上公式解题。
例. 计算:()()()()111124-+++a a a a例. 计算:()()57857822a b c a b c +---+例.(1)已知a b ab -==45,,求a b 22+的值。
(2) 已知2=+b a ,1=ab ,求22b a +的值。
(3) 已知8=+b a ,2=ab ,求2)(b a -的值。
(4) 已知x-y=2,y-z=2,x+z=14。
求x 2-z 2的值。
例:计算19992-2000×1998 例.已知13x x-=,求441x x +的值。






专题训练 乘法公式的灵活应用► 类型一 变形乘法公式巧求式子的值1.阅读:已知a +b =-4,ab =3,求a 2+b 2的值.解:∵a +b =-4,ab =3,∴a 2+b 2=(a +b )2-2ab =(-4)2-2×3=10.已知a +b =6,ab =2,请你根据上述解题思路求下列各式的值.(1)a 2+b 2;(2)(a -b )2;(3)a 2-ab +b 2.2.我们知道完全平方公式(a +b )2=a 2+2ab +b 2,(a -b )2=a 2-2ab +b 2.两式相加得(a +b )2+(a -b )2=2a 2+2b 2,即a 2+b 2=12[(a +b )2+(a -b )2];两式相减得(a +b )2-(a -b )2=4ab ,即ab =14[(a +b )2-(a -b )2]. 请利用以上性质完成下列问题:已知(x +y )2=6,(x -y )2=2,试求:(1)x 2+y 2的值;(2)xy 的值.3.阅读下列解题过程:已知x ≠0,且满足x 2-3x =1,求x 2+1x 2的值. 解:∵x 2-3x =1,∴x 2-3x -1=0.又∵x ≠0,∴x -3-1x =0,即x -1x=3. ∴x 2+1x 2=⎝⎛⎭⎫x -1x 2+2=32+2=11. 请根据上述解题思路解答下列问题:若a 2-5a -1=0,且a ≠0,求a 2+1a 2的值.► 类型二 巧用乘法公式简便计算4.利用乘法公式简便计算:(1)-992;(2)20192-2018×2020;(3)20817×19917.► 类型三 巧用乘法公式化简求值5.数学课上老师出了一道题:计算2962的值.喜欢数学的小亮举手回答这道题,他的解题过程如下:2962=(300-4)2(第一步)=3002-2×300×(-4)+42(第二步)=90000+2400+16(第三步)=92416.(第四步)老师表扬小亮积极发言的同时,也指出了他解题过程中的错误.(1)你认为小亮的解题过程中,从第几步开始出错?(2)请你写出正确的解题过程.6.2018·江西 计算:(a +1)(a -1)-(a -2)2.7.先化简,再求值:(2a +b )(2a -b )-(3a -b )2+6a (a -b ),其中a =37,b =1.►类型四逆用乘法公式8.观察下列等式:1×32×5+4=72=(12+4×1+2)22×42×6+4=142=(22+4×2+2)23×52×7+4=232=(32+4×3+2)24×62×8+4=342=(42+4×4+2)2…(1)根据你发现的规律,求12×142×16+4是哪一个正整数的平方;(2)请把n(n+2)2(n+4)+4(n是正整数)写成一个正整数的平方的形式.9.2018·武汉市江汉区校级月考阅读材料:若m2-2mn+2n2-8n+16=0,求m,n的值.解:∵m2-2mn+2n2-8n+16=0,∴(m2-2mn+n2)+(n2-8n+16)=0.∴(m-n)2+(n-4)2=0.∵(m-n)2≥0,(n-4)2≥0,∴(m-n)2=0,(n-4)2=0.∴n=4,m=4.根据你的观察,探究下面的问题:(1)已知x2+2xy+2y2+2y+1=0,求2x+y的值;(2)已知△ABC的三边长a,b,c都是正整数,且满足a2+b2-12a-16b+100=0,求△ABC的最大边长c的值.►类型五乘法公式与图形面积10.解放街幼儿园有一个游戏场和一个葡萄园,其所占地的形状都是正方形,面积也相同.后来重新改建,扩大了游戏场,缩小了葡萄园,扩大后的游戏场地仍为正方形,边长比原来增加了3米,缩小后的葡萄园也为正方形,边长比原来减少了2米,设它们原来的边长为x米,请求出扩大后的游戏场地比缩小后的葡萄园的面积多多少平方米,并计算当x=12时式子的值.11.如图1①所示,边长为a的正方形中有一个边长为b的小正方形(a>b),如图②所示是由图①中的阴影部分拼成的一个长方形.(1)设图①中阴影部分的面积为S1,图②中阴影部分的面积为S2,请直接用含a,b的式子表示S1,S2;(2)请写出上述过程所揭示的乘法公式;(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.图1详解详析1.解:(1)∵a +b =6,ab =2,∴a 2+b 2=(a +b )2-2ab =62-2×2=32.(2)∵a 2+b 2=32,ab =2,∴(a -b )2=a 2+b 2-2ab =32-4=28.(3)∵a 2+b 2=32,ab =2,∴a 2-ab +b 2=a 2+b 2-ab =32-2=30.2.解:(1)x 2+y 2=12[(x +y )2+(x -y )2]=12×(6+2)=4. (2)xy =14[(x +y )2-(x -y )2]=14×(6-2)=1. 3.解:∵a 2-5a -1=0且a ≠0,∴a -5-1a =0,即a -1a=5. ∴a 2+1a 2=(a -1a)2+2=52+2=27. 4.解:(1)原式=-(100-1)2=-(10000-200+1)=-10000+199=-9801.(2)原式=20192-(2019-1)(2019+1)=20192-(20192-12)=20192-20192+1=1.(3)20817×19917=(20+817)×(20-817)=202-(817)2=400-64289=399225289. 5.解:(1)从第二步开始出错.(2)正确的解题过程如下:2962=(300-4)2=3002-2×300×4+42=90000-2400+16=87616.6.解:原式=a 2-12-(a -2)2=a 2-1-(a 2-4a +4)=a 2-1-a 2+4a -4=4a -5.7.解:原式=4a 2-b 2-9a 2+6ab -b 2+6a 2-6ab =a 2-2b 2.当a =37,b =1时,原式=949-2=-14049. 8.解:(1)由题意,可得12×142×16+4=(122+4×12+2)2=1942,所以12×142×16+4是194的平方.(2)n (n +2)2(n +4)+4=(n 2+4n +2)2(n 是正整数).9.解:(1)∵x 2+2xy +2y 2+2y +1=0,∴(x 2+2xy +y 2)+(y 2+2y +1)=0.∴(x +y )2+(y +1)2=0.∵(x +y )2≥0,(y +1)2≥0,∴(x +y )2=0,(y +1)2=0.∴y =-1,x =1.∴2x +y =2-1=1.(2)∵a 2+b 2-12a -16b +100=0,∴(a 2-12a +36)+(b 2-16b +64)=0.∴(a -6)2+(b -8)2=0.∵(a -6)2≥0,(b -8)2≥0,∴(a -6)2=0,(b -8)2=0.∴a =6,b =8.∴8-6<c <8+6,即2<c <14.又∵c ≥8,c 为正整数,∴8≤c <14,且c 为整数.∴△ABC 的最大边长 c 的值可能是8,9,10,11,12,13.10.解:(x +3)2-(x -2)2=(x 2+6x +9)-(x 2-4x +4)=x 2+6x +9-x 2+4x -4=(10x +5)米2.即扩大后的游戏场地比缩小后的葡萄园的面积多(10x +5)平方米.当x =12时,原式=10×12+5=125.11.解:(1)S1=a2-b2,S2=(a+b)(a-b).(2)(a+b)(a-b)=a2-b2.(3)原式=(2-1)(2+1)(22+1)(24+1)(28+1)+1 =(22-1)(22+1)(24+1)(28+1)+1=(24-1)(24+1)(28+1)+1=(28-1)(28+1)+1=(216-1)+1=216.。
乘法公式·要点全析
1.平方差公式(formula for the difference of squares )
(1)表达式:(a +b )(a -b )=a 2-b 2.
(2)语言叙述:
两个数的和与这两个数的差的积,等于这两个数的平方差.
(3)注意事项:
①运用公式要抓住公式的结构特征,左边是两个数的和与这两个数的差相乘,右边正好是这两个数的平方差,对于形如两数和与这两数差相乘,就可运用上述公式计算.
②公式中的字母可表示具体的数,也可表示单项式或多项式,只要符合公式的结构特征,就可运用该公式.
③在运用公式时,要求分清哪个数相当于公式中的a ,哪个数相当于公式中的b ,按公式的结构相乘.
例如:①(m +4)(m -4)=
②(2a 2+3b )(2a 2-3b )=.
③(-43xy 3-32x 3)(43
xy 3-32x 3)
=
2.完全平方公式(formula for the square of the sum )
(1)字母表达式:
(a +b )2=a 2+2ab +b 2,(a -b )2=a 2-2ab +b 2.
可合写为(a ±b )2=a 2±2ab +b 2.
(2)语言叙述:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.右面可说为:“首平方,尾平方,首尾之积的2倍加减在中央”.
(3)注意事项:
①对于形如两数和(或差)的平方运算,可运用完全平方公式计算.利用公式计算时,首先确定将哪个数或式看作a ,将哪个看作b ,再按公式结构展开. ②这两个公式,是据乘方的意义与多项式的乘法法则得到的. ③公式中的a 、b 可表示具体的一个数或其他的一个代数式. ④可推广:如(a +b +c )2=a 2+b 2+c 2+2ab +2ac +2bc .
(a +b +c +d )2=a 2+b 2+c 2+d 2+2ab +2ac +2ad +2bc +2bd +2cd .……
3.平方差公式的灵活运用
有些式子在计算时,不能直接利用平方差公式,需要稍加变形或变式后,才能使用.常用的方法有如下几种:
(1)调换位置.
如:(1+2a )(-2a +1)=(1+2a )(1-2a )=1-4a 2.
(2)提取-1或其他公因式.
如:(-a -b )(a -b )=
又如:(6x +2y )(3x -4y
)=
(3)分组.
如:(a-b+c-d)(a+b-c-d)
=
(4)运用积的乘方变形.
如:(a-b)2 (a+b)2
=
(5)将乘式同时乘以并且同时除以一个适当的因式.
如:(2+1)(22+1)(24+1)(28+1)
=
…
又如:(1-m)(1+m2)(1+m4)(m≠-1)
=
(6)把一个因式适当变形.
如:3(22+1)(24+1)(28+1)
=
(7)将因式多项式拆项或添项.
如:(a-b)(a+2b)
=
4.完全平方公式的灵活运用
a2+b2=(a+b)2-2ab,
a2+b2=(a-b)2+2ab,
(a+b)2+(a-b)2=2(a2+b2),
(a+b)2-(a-b)2=4ab.
(1)恒等式a2+b2=(a+b)2-2ab和a2+b2=(a-b)2+2ab的应用.在此恒等式中,有三个量a2+b2、(a+b)2或(a-b)2、ab,若已知任意两个,则可求第三个,求得(a+b)2或(a-b)2,也就求得a+b或a-b.例如:①若a2+b2=3,ab=1,可求(a+b)2.
②若a-b=3,ab=4,则可求a2+b2.
(2)恒等式(a+b)2+(a-b)2=2(a2+b2)的应用.
在恒等式(a+b)2+(a-b)2=2(a2+b2)中,有三个量a+b、a-b、a2+b2,若已知两个量,就可求第三个量.
例如:已知a-b=-1,a2+b2=5.求a+b.
解:
(3)恒等式(a+b)2-(a-b)2=4ab的应用.
在此等式中,有三个量a+b,a-b,ab.若知任两个量,可求第三个量.例如:已知a-b=1,ab=2,求a+b.
解:
(4)利用完全平方公式,求平方数.
如:152= 232=
672=.
79.22=
(5)完全平方数是非负数.
任何一个完全平方数M都能化为n2的形式,即M=n2,由偶次幂的性质得n2≥0.当n=0时,n2的最小值是0,并且n2具有非负数的性质,即若n个非负数的和为0,则这几个非负数就同时为0.
因此,(a±b)2≥0.当a±b=0时,(a±b)2的最小值为0.
例如:①已知(x+y-1)2+(x-2)2=0,则x=_______,y=___________.解:
例如:②已知,a、b为自然数,且a+b=2,求ab的最大值及a、b的值.解:
5.完全平方公式的逆运用,即a2±2ab+b2=(a±b)2
把一个形如a2±2ab+b2的二次三项式化为(a±b)2的形式,然后运用(a ±b)2的性质求解问题.
例如:已知x2+4x+y2-2y+5=0,求x、y的值.
解:
再如:已知a2+b2+c2=ab+ac+bc,则a、b、c的关系为_______.
解:
也可以运用公式a2±2ab+b2=(a±b)2把一类二次三项式直接化为(a±b)2的形式.如4x2-4xy+y2=(2x)2-2×2x×y+y2=(2x-y)2.
6.完全平方式
因为a2±2ab+b2能化成(a±b)2的形式,所以,形如a2±2ab+b2的式子叫做完全平方式,其中a、b表示代数式.
例如:①已知x2+4x+k是完全平方式,求常数k的值.
解:
②已知x 2+2kx +4是完全平方式,求常数k 的值.
解:
思考题;已知x 2+M +4是一个完全平方式,求代数式M (提示:①当M 为常数项时;②当M 为乘积项,即“一次项式”时;③当M 为“二次项式”时.并分析在三种情况下,M 的值有多少个.)
注意:完全平方数是完全平方式的特例.
总之,完全平方公式,应用广泛,灵活,具有丰富的方法和技巧.
7.平方差公式可变形后运用
(1)可变形为a 2=(a +b )(a -b )+b 2,可快速求两位数的平方. 如:352=(35+5)(35-5)+52=1 225.
972=(97+3)(97-3)+32=100×94+9=9 409.
(2)在(a +b )(a -b )=a 2-b 2中,有三个多项式,若已知任意两个的值,即可求第三个的值.
如:已知a +b =3,a 2-b 2=4,则a -b =--------
.
(3)对公式(a +b )(a -b )=a 2-b 2的逆运用,即利用公式a 2-b 2=(a +b )(a -b )求解问题.(其实(a +b )(a -b )=a 2-b 2和a 2-b 2=(a +b )(a -b )都是平方差公式)
如:①x 2-4=
②1-4a 2b 2=
③(a +b )2-(a -b )2=
④(1-221)(1-231)(1-241)…(1-2101
)
=。