当前位置：文档之家 › 固体物理倒格矢课件

固体物理倒格矢课件

  • 格式：ppt
  • 大小：2.95 MB
  • 文档页数：41

下载文档原格式

  / 41

合集下载

固体物理倒格矢

固体物理倒格矢

—— 第一布里渊区
原点和12个近邻格点连线的垂直平分面围成的正十二面体
倒格矢 K n n1 b n2 b n3 b 3 1 2 2 [( n2 n3 )i (n1 n3 ) j (n1 n2 )k ] a



体心立方的倒格子是面心立方，离原点最近的有 十二个倒格点，在直角坐标系中它们的坐标为：
二维长方晶格的布里渊区
二维六方晶格的十个布里渊区
(3) 三维晶格
a. 简立方晶格
b1 a1 ai a 2 aj b2 a 3 ak b 3
倒易空间示意图
2 a 2 a 2 a i j 倒易点阵仍为简立方晶 格 k
( Rl和Gh 不一定平行)
可见， Rl和 Gh的量纲是互为倒逆的， Rl是格点P的位 置矢量，称为正矢量， kh称为倒易矢量。 若令Gh= h1b1+h2b2+h3b3， 则称由b1，b2，b3为基矢构成的点阵为倒易点阵. (b1，b2，b3)如何确定？
1.9.2 倒格子空间(倒易点阵)*
（1）.倒矢与正格矢的关系：
离原点最近的倒 格点有４个： b1，-b1，b2，-b2．
-b1
b2
b1 －b2
离原点次近的倒 格点有４个： -b1＋b2 b1＋b2 ，b1-b2 ，b2， -b2．
b1 ＋b2
－b1-b2
b1-b2
离原点再远的倒格点有４个： ２b1，-２b1，２b2，-２b2．
２b２
－２b1
２b1
－２b２
二维正方晶格的布里渊区
(2) 两个点阵格矢之间的关系： 正点阵： 正格矢 Rl l1a1 l2a2 l3a3 l1、l2、l3 Z 倒易点阵： 倒格矢Gh h1b1 h2b2 h3b3 h1、h2、h3 Z 则有： Rl Gh ＝ 2 Z 结论： 若两矢量点积为2的整数倍， 且其中一个矢量 为正点阵位矢， 则另一个矢量必为倒易点阵的位矢。

1.3倒格子-固体物理

1.3倒格子-固体物理

方法2：利用
b2 2π a 3 a1 Ω
2π
b3 a1 a2 Ω
a2 a2 j
a1 a1 i
a1 a1 i
正格子
a2
a2
j
假定 a3 k ，则 Ω a1 a2 a3 a1a2
2π
2 2
b1 Ω a 2 a 3 a1a2 a2i a1 i
b2 2π Ω
Rn n1a1 n2 a2 n3 a3
倒格子 倒格基矢 b1,b2 ,b3 倒格（点位）矢：
K n h1b1 h2b2 h3b3
每一个布拉菲格子都有一与之相对应的倒格子
一、倒格子定义
倒格子基矢定义为：
b1 2π a2 a3 Ω
b2 2π a3 a1 Ω
b3 2π a1 a2 Ω
同理得：
b2
2π a
ik
b3
2π a
i
j
2π
a3
a2 2
j k 2π a
jk
2
倒格矢：
b1
2π a
jk
b2
2π a
ik
b3
2π a
i
j
FCC基矢：
a
a1 i j 2
a 2 a j k 2 a a3 k i
2
体心立方的倒格子是边长为4/a的面心立方 。
Rl l1 a1 l2 a 2 l3 a 3 K h h1 b1 h2 b2 h3 b3
Rl K h (l1 a1 l2 a 2 l3 a 3 ) ( h1b1 h2 b2 h3 b3 )
2π( l1h1 l2h2 l3h3 )
2π ( i j )
2π
a i b j 2π ij

1-4倒格子ppt课件

1-4倒格子ppt课件

证明提示：设晶面ABC是晶面族 （h1h2h3）中最靠近原点的晶面，
截距分别为
a1 , a2 , a3 h1 h2 h3
a3
G
C
a3/h3
B a2
O
a2/h2
a1/h1
A
a1
思路：能证明 G 同时垂直于CA 和CB ，即能证明 G 垂直
于面ABC。 9
简单证明如下：

G
为正格子原胞体积
正格子空间 （或正点阵）
倒格子空间 （或倒易点阵）
2
2、倒格子与正格子的关系
2.1 数学描述
空间
基矢
正格子空间 倒格子空间
a1, a2 , a3
b1

2
a2
a3

v
b2

2
a3 a1 v
b3

2
a1 a2

v
位置矢量 R l1a1 l2a2 l3a3
a
K h h1b1 h2 b2
倒格是边长为
2π
的正方形格子。
a
24
例2：证明体心立方的倒格是面心立方。
解： 体心立方的原胞基矢：
a
a1 i j k 2
a
a2 i j k 2
a 3 a i j k 2
b1 2π a2 a3 Ω
j
b1
2π a
jk
b2
2π a
ik
2π
b3 a i j
体心立方的倒格是边长为4/a的面心立方 。
26
例3：证明简立方晶面(h1h2h3)的面间距为

固体物理03-倒格子空间

固体物理03-倒格子空间

4
dr
nj
(r )r 2
sin Gr Gr
实验发现固体中的原子形状因子与自由原子的差别不大
其它实验手段
1. 电子衍射 （动量空间）
与X射线相比，电子波长更短，所以更加精确；更容易被物体吸收适 合于研究微薄膜、小晶体。
2. 中子散射 （动量空间）
可以测量晶体磁结构
3. 扫描隧道显微镜（实空间，表面）
S v1v2v3 f {1 exp i v2 v3 exp i v1 v3 exp i v1 v2 }
S 4 f 所有指数均为奇数，或均为偶数 S 0 其它情况
面心立方 的x-ray 散射图像
原子形状因子 f j dV n j (ρ)eiGρ
对自由原子：
f j 2 dr r 2 d cos n j exp(iGr cos )
j
ρ r rj
定义原子的形状因子 f j dV n j (ρ)eiGρ
结构因子
化简后可以得到晶体的结构因子
SG
f eiGr j j
j
对于第 j 个原子
G rj v1b1 v2b2 v2b2 x ja1 y ja2 z ja3 2 v1x j v2 y j v3z j
散射幅度
SG
dV n(r)eiGr
cell
结构因子
结构因子
假设晶胞中有 s 个原子，可以把原胞中的电荷密度分配到每一 个原子上（分配方法不唯一），即:
s
n(r) n j (r rj )
j 1
SG
cell dV n j (r r j )eiGr
j
eiGrj cell dV n j (ρ)eiGρ
晶体点阵的Fourier变换，晶体点阵则是倒易点阵的Fourier逆 变换。正格子的量纲是长度 L, 称作坐标空间，倒格子的量钢是 长度的倒数 L-1，称作波矢空间（或称动量空间）。

高二物理竞赛倒格子、布里渊区PPT(课件)

高二物理竞赛倒格子、布里渊区PPT(课件)

13
2
2
0
(h1, h2 , h3 0, 1, 2, 3, )
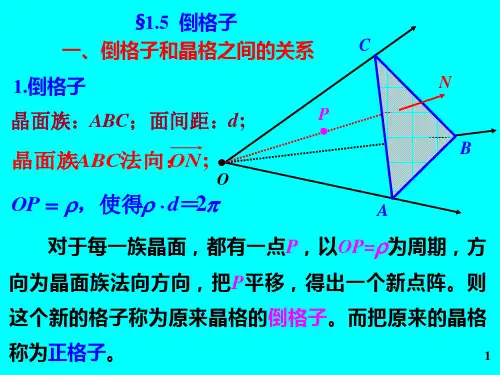
在倒格子空间中，满足上式的 k 的端点的集合构成布里渊区界面，称为布里渊区 界面方程。
a
ai , a
aj
三、晶格周期函数的傅立叶展开
按定义，布里渊区界面是倒格矢 G
的垂直平分面，设倒格子空间矢量为 k ，如
G CA (h1b1 h2b2 h3b3 )
a1 h
1
G G
a
1
1
h1 G
h1b1 h2b2 h3 b3
2
G
(h1, h2, h3 0,1,2,3,)
三、晶格周期函数的傅立叶展开
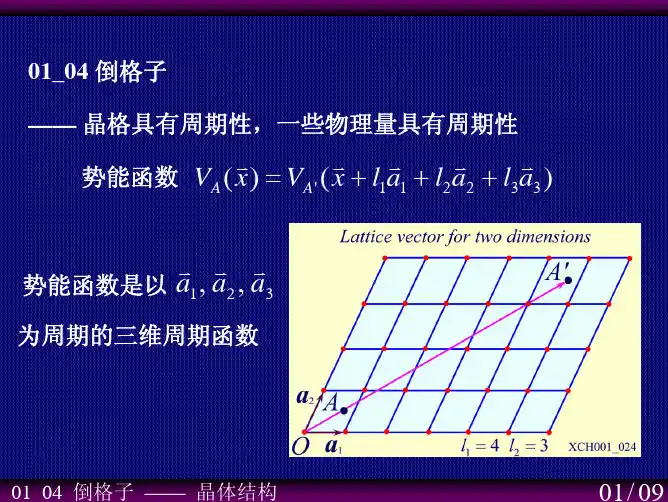
晶格周期函数
VR(nr：晶Rn格) 平V移(r矢) 量，r 晶格中某点的位置坐标，
r a a a
11 2 2 3 3
k kxi ky j 得到第一布里渊区界面方程： k 倒格矢与正格子晶面系的关系： 得到在ABC面上的两个矢量： 按定义，布里渊区界面是倒格矢 G k kxi ky j
V ( 1 1), ( 2 1), ( 3 1)
倒,k 格,k 子、布里渊区
的垂直平分面，设倒格子空间矢量为 k ，如
G CA (h1b1 h2b2 h3b3 )
0), (n1 1),(n
1, 0,
n2 n
0), 1)
1
2
1
2
得到第一布里渊区界面方程：
kx
a
,kx
a
,ky
a
,k y
a
ky
第一布里渊区
kx
a
kx
a
ky
a
kx
G1
k
y

固体物理§1.5倒格子

固体物理§1.5倒格子

r r r Kh ⊥ CA Kh ⊥ CB ⇒ Kh ⊥ 晶面 ABC。 ，
9
r 3.倒格矢 Kh和面间距的关系 倒格矢 晶面ABC为晶面族中最靠近原点的晶面。 为晶面族中最靠近原点的晶面。 晶面 为晶面族中最靠近原点的晶面
dh1h2h3 r a1 = ⋅ h1
r r r r r Kh a1 ⋅ h1b1 + h2b2 + h2b3 r = r Kh h1 Kh
( Ω Ω＝2π )
∗
3
3 r r r (2π ) (a a ) [(a a ) (a a )] r r r r r r ∗ Ω = b1 ⋅ (b2 × b3 ) = 2× 3 ⋅ 3× 1 × 1× 2 3 Ω r r r r r r r r r 利用： A 利用： × (B × C) = ( A⋅ C)B − ( A⋅ B)C r r r r r r r r r r r r r (a3 × a1 ) × (a1 × a2 ) = [(a3 × a1 ) ⋅ a2 ]a1 − [(a3 × a1 ) ⋅ a1 ]a2 = Ωa1
1
2.倒格子基矢和正格子基矢之间的关系 倒格子基矢和正格子基矢之间的关系
r r r r r r 正格子基矢： a 正格子基矢： 1、a2、a3；倒格子基矢： 1、b2、b3; 倒格子基矢： b
晶面族： a d 晶面族： 1a2、a2a3、a3a1的面间距分别为 3、d1、d2;
r b3
r a3
r b2
3.倒格矢和正格矢的关系 倒格矢和正格矢的关系
r r r r r r r r Kh ⋅ Rl = (l1a1 + l2a2 + l3a3 ) ⋅ (h b1 + h2b2 + h3b3 ) 1 = 2πµ (µ为整数)

固体物理学 倒格子

(2π ) v v v v = 2 ( a2 × a3 ) ⋅ a1 v0
3 * 0
(2π ) v = v0
* 0
3
01 04 倒格子 —— 晶体结构
2) 正格子中一簇晶面 ( h1 h2 h3 ) 和
v Gh1h2h3 正交
v v v v Gh1h2h3 = h1b1 + h2b2 + h3b3
—— 积分在一个原胞中进行
01 04 倒格子 —— 晶体结构
—— 倒格子与正格子间的关系 1) 正格子原胞体积反比于倒格子原胞体积
v v v * v0 = b1 ⋅ (b2 × b3 )
3
v v v v v v v v v A × B × C = ( A ⋅ C ) B − ( A ⋅ B )C
(2π ) v v v v v v = ( a2 × a3 ) ⋅ ( a3 × a1 ) × ( a1 × a2 ) 3 v0
v v v a2 × a3 b1 = 2π v v v a1 ⋅ a2 × a3
v v v v v v a3 × a1 a1 × a2 b2 = 2π v v v b3 = 2π v v v a1 ⋅ a2 × a3 a1 ⋅ a2 × a3
v v v 以 b1 , b2 , b3 为基矢构成一个倒格子
01 04 倒格子 —— 晶体结构
v 3) 倒格子矢量 Gh1h2h3 为晶面( h1h2 h3 ) 的法线方向
v v v v 晶面方程 ( h1b1 + h2b2 + h3b3 ) ⋅ x = 2πn
各晶面到原点O点的距离
v v v (2π n ) / h1b1 + h2b2 + h3b3
v v ai ⋅ b j = 2πδ ij

倒格子

倒格子（倒易点阵） 倒格子（倒易点阵）
倒格子的定义： 倒格子的定义：
• 在固体物理学中：实际观测无法直接测量 在固体物理学中： 正点阵， 正点阵，倒格子的引入能够更好的描述很 多晶体问题， 多晶体问题，更适于处理声子与电子的晶 格动量。 格动量。 • 在X射线或电子衍射技术中：一种新的点阵， 射线或电子衍射技术中： 射线或电子衍射技术中 一种新的点阵， 该点阵的每一个结点都对应着正点阵中的 一个晶面，不仅反映该晶面的取向， 一个晶面，不仅反映该晶面的取向，还反 映着晶面间距。 映着晶面间距。
b1 =
2
(a ×a ) a ⋅ (a ×a ) 1 (a ×a ) b = a ⋅ (a ×a )
1
2 2 3 1 3 3 1
b3 =
(a ×a ) a ⋅ (a ×a )
1
1 1 2 3 2
2
3
1
确定倒格矢的方法：对于一切整数 h,k,l,作出 作出 ( hb1 + k b 2 + l b3),这些向 这些向 量的终点就是倒格 子的节点。 子的节点。
倒格子（倒易点阵）的基本性质： 倒格子（倒易点阵）的基本性质：
• 正点阵与倒易点阵的同名基矢的点积为 ，不同 正点阵与倒易点阵的同名基矢的点积为1， 名基矢的点积为零； 名基矢的点积为零； • 正点阵晶胞的体积与倒易点阵晶胞的体积成倒数 关系； 关系； • 正点阵的基矢与倒易点阵的基矢互为倒易； 正点阵的基矢与倒易点阵的基矢互为倒易； h • 任意倒易矢量（ b1 + kb2 + lb3 ）垂直于正点阵中的 任意倒易矢量（ （hkl）面； ） • 倒易矢量的模等于正点阵中晶面间距的倒数。 倒易矢量的模等于正点阵中晶面间距的倒数。
• 任何一个晶体结构都有两个格子：一个是 任何一个晶体结构都有两个格子： 正格子空间(位置空间 位置空间)， 正格子空间 位置空间 ，另一个为倒格子空 状态空间)。 间(状态空间 。二者互为倒格子，通过傅里 状态空间 二者互为倒格子， 叶变换。 叶变换。晶格振动及晶体中电子的运动都 是在倒格子空间中的描述。 是在倒格子空间中的描述。

固体物理(第4课)倒易空间课件


V* b1 (b2 b3 )
(2 )3
V
可见V*与V互为倒数
上式利用了 A B C ( A C)B ( A B)C
(4) 倒格矢和正点阵晶面族之间的关系：
正点阵中一族晶面，晶面指数为：（h1h2h3）
倒易点阵中倒格矢：
Gh
h1b1 h2b2
h3b3
则有：
GGhh
Γ (r)为周期函数
将Γ (r)作傅里叶级数展开，有：
Γ (r)＝ C e C e n1 n2 n3
iGn
r
n
n
iGn
r
n
n1 n2 n3
n
学习交流PPT
11总Biblioteka ：晶体点阵 实际晶体结构显微图像 微观粒子 线度量纲：L 位置空间 坐标空间
倒易点阵 虚构
衍射图像 一族晶面 线度量纲：L－1 倒易空间 傅里叶空间
aa13aa33
2
a
2
a
i j
离原点最近的倒 格点有４个： b1，-b1，b2，-b2．
-b1
b2
b1 －b2
学习交流PPT
14
离原点次近的倒
格点有４个：
b1＋b2 ，b1-b2 ，
b2，-b2．
-b1＋b2
b1＋b2
－b1-b2
b1-b2
学习交流PPT
15
离原点再远的倒格点有４个：
２b1，-２b1，２b2，-２b2．
Z
h1、h2、h3 Z
结论： 若两矢量点积为2的整数倍， 且其中一个矢量
为正点阵位矢， 则另一个矢量必为倒易点阵的位矢。
学习交流PPT
7
•为什么在倒易关系中存在2π 因子，这是因为如此定 义的互为倒易的两个矢量G与T之间满足下面简洁的

固体物理第二章第四节 倒格子.

h1 Gh h1 Gh h1 Gh Gh
2
d h1h2h3 Gh
表明,对任一倒格矢Gh h1b1 h2b2 h3b3
以其在倒易空间的坐标数(h1，h2，h3)表征的
正格子空间中的晶面族(h1h2h3)，一定以 Gh
为法线方向，且面间距为 2 / Gh
这个关系很重要,后面分析XRD时要用
3.倒格子基矢的方向和长度
许多的固体书中把上述描述作为倒格子的定义
2. 与正格子空间的平面波 类eiG似h•r，可以把
看成ei倒g•R空l 间的平面波， 是倒空间g的任一矢量
e e • e e i(gGh )•Rl
ig • Rl
iGh •Rl
ig • Rl
所以，在倒空间中，矢量 与g
代表相同的波或相同的状态。
g Gh
b1
2π a
j k
b2
2π a
i k
b3
2π a
i
j
体心立方的倒格子是边长为4/a的面心立方 。
例3：证明简立方晶面(h1h2h3)的面间距为
a
d h1h2h3
证明：
h12 h22 h32
由于 a为1,基a2,矢a3，互不共面，则由
bi • aj 2可知ij
亦b应1, b该2 , b不3 共面，从而可以用
描述倒格子Gh。 h1b1 h2b2 h3b3
由于 Gh h1b1 h2为b2 倒 h格3b3矢，如果把倒格矢所在 的空间称为倒格子空间，或倒易空间(reciprocal
2
a
a a a
2
2 j 2
a
a
2
2
2 k 2 aa 22
2 a 2
22
2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1.9 倒格子(倒易点阵reciprocal)*
学习交流PPT
1
1.9 1 倒格子(倒易点阵)*的定义：
•1 正格矢与倒矢
S S0 P
原子可向空间任何方向散射 X光线，只有一些固定方向 可形成衍射。
B AO
•点P： Rl=l1a1+l2a2+l3a3，Rl是布喇菲点阵中由原胞基 矢a1，a2，a3构成的矢量，
•根据正点阵与倒易点阵的关系，(k-k0)必是倒易空间
中的位置矢量，令：
Gh k -k0
2
(S
S0 )
•有
Rl• Gh = 2π u ( 学习交流PPT Rl和Gh 不一定平行)
3
•可见， Rl和 Gh的量纲是互为倒逆的， Rl是格点P的位 置矢量，称为正矢量， kh称为倒易矢量。 •若令Gh= h1b1+h2b2+h3b3， •则称由b1，b2，b3为基矢构成的点阵为倒易点阵.
aa13aa33
2
a
2
a
i j
离原点最近的倒 格点有４个： b1，-b1，b2，-b2．
-b1
b2
b1 －b2
学习交流PPT
14
离原点次近的倒
格点有４个：
b1＋b2 ，b1-b2 ，
b2，-b2．
-b1＋b2
b1＋b2
－b1-b2
b1-b2
学习交流PPT
15
离原点再远的倒格点有４个：
２b1，-２b1，２b2，-２b2．
２b２
－２b1
２b1
－２b 学习交流PPT
２
16
二维正方晶格的布里渊区
学习交流PPT
17
二维长方晶格的布里渊区
学习交流PPT
18
二维六方晶格的十个布里渊区
学习交流PPT
19
学习交流PPT
20
(3) 三维晶格
• a. 简立方晶格 倒易空间示意图
aaa321
ai
aj
ak
b1
b2
•S0和S是入射线和衍射线的单位矢量，经过O点和P点衍 射后光程差为：
A0 OB -Rl S0 RlS Rl (S-S0)
学习交流PPT
2
•当X光为单色光，衍射加强的条件为：
•
Rl•(S-S0)=u •λ
•令
k
2
S
k0
2
S0
，代入上式，
•衍射加强条件变为： Rl• （k -k0） = 2π u
Z
h1、h2、h3 Z
结论： 若两矢量点积为2的整数倍， 且其中一个矢量
为正点阵位矢， 则另一个矢量必为倒易点阵的位矢。
学习交流PPT
7
•为什么在倒易关系中存在2π 因子，这是因为如此定 义的互为倒易的两个矢量G与T之间满足下面简洁的
恒等式：
•
eiGT 1
学习交流PPT
8
(3) 两个点阵原胞体积之间的关系：
a1、 a2、 a3： 原胞基矢 正点阵
学习交流PPT
5
V
b1 b2 a1 b 3(a2
2 a2 a3
2 a3V a1
2
a1
V
a2
a3
)
V 原胞体积
12：：bb11的方2d向1 沿a2、d1是a3构a2、成a的3构晶成面的的晶法面线族方的向面间距
学习交流PPT
6
（2）. 倒格子点阵与正格子点阵的关系
K空间
学习交流PPT
12
1.9.3 常见晶格的布里渊区
•(1) 一维晶格
a1
ai
b1
2
a
i
(2) 二维晶格
a1、a2
构 造a3， 令a3＝k
b1
b2
2 2
a1 a1
aa2学3aa习22交aa流31PaaPT33
13
aa12
ai aj
b1
b2
2 2
a1 a1
aa23aa22
(1) 两个点阵基矢之间的关系：
ai
bj
2 ij
2，i
0，i
j j
b1 b2 b3
2 2 2
a2 a3
a3V a1
a1
V
a2
V
(2) 两个点阵格矢之间的关系：
正点阵：
正格矢
Rl
l1a1
l2a2
l3a3
l1、l2、l3 Z
倒则易有点： 阵：倒格矢Rl G Gh h＝2h1b1
h2b2 h3b3
Γ (r)为周期函数
将Γ (r)作傅里叶级数展开，有：
Γ (r)＝ C e C e n1 n2 n3
iGn
r
n
n
iGn
r
n
n1 n2 n3
n
学习交流PPT
11
总结：
晶体点阵 实际晶体结构
显微图像 微观粒子 线度量纲：L 位置空间 坐标空间
倒易点阵 虚构
衍射图像 一族晶面 线度量纲：L－1 倒易空间 傅里叶空间
V* b1 (b2 b3 )
(2 )3
V
可见V*与V互为倒数
上式利用了 A B C ( A C)B ( A B)C
(4) 倒格矢和正点阵晶面族之间的关系：
正点阵中一族晶面，晶面指数为：（h1h2h3）
倒易点阵中倒格矢：
Gh
h1b1 h2b2
h3b3
则有：
GGhh
b 4π a
•体心立方晶格的倒易晶格是面心立方，其晶胞
常数为 4 。
a
学习交流PPT
22
c. 面心立方晶格
a1 a2 a3
a
2 a
2 a
2
(j (i (i
k) k) j)
b3
2
a
2
a
2
a
i j k
b1
倒易点阵仍为简立方晶格
b3 b2
学习交流PPT
b1
21
b. 体心立方晶格 倒易空间示意图
a1
பைடு நூலகம்
a 2
(
a2 a3
a
2 a
2
i j k) (i j k) (i j k)
b1
b2
b3
2π
a 2π
a 2π
a
(j k) (i k) (i j)
// (h1h2h3
＝ 2
d h1h2h3
)
法线方向
证明如下：
(5)倒易点阵与正点阵互为倒易点阵
(6)倒易点阵与正点阵学有习交流相PPT同的宏观对称性
9
倒格矢和正点阵晶面族示意图
CA＝OA OC a1 a3
CB＝OB
OC
h1 a2
ah33
h2 h3
CA
Gh
0
Gh
CA
CB Gh 0 Gh CB
d h1h2 h3＝ah11
Gh Gh
a1
(h1b1
h2b2
h3b3 )
h1 Gh
2
Gh
学习交流PPT
返回
10
•3.倒易点阵与傅里叶变换
Γ
若(r)有rr＝ rx1a1Rl，x2Ral2
x3a3 l1a1
x1、x2、x3 l2a2 l3a3
R l1、l2、l3
Z
则有Γ (r) Γ (r) (示意图)
•(b1，b2，b3)如何确定？
学习交流PPT
4
1.9.2 倒格子空间(倒易点阵)*
•（1）.倒矢与正格矢的关系：
点阵：原胞基 矢a1、a2、a3
b1 2 b2 2 •b3 2
a2 a3
a3V a1 ， V
a1
V
a2
V
a1 (a2
a3 )
原胞体积
b1、 b2、 b3： 原胞基矢 倒易点阵