固体物理倒格矢
- 格式:ppt
- 大小:2.98 MB
- 文档页数:42



简述倒格子点阵的物理意义
倒格子点阵是固体物理学中的一个重要概念,用于描述晶体中离子、原子或分子的排列方式。
它表示了晶体中离子在晶格中的周期性排列。
倒格子点阵在物理意义上具有以下重要特征:
1.倒格子与晶体结构的相互关系:倒格子是晶体格矢的补格。
晶体格矢是描述晶体结构的向量,而倒格子则是晶格矢的傅里叶变换。
倒格子点阵的形状和大小与晶体结构紧密相关。
2.表征晶体的动量空间:倒格子点阵的形成使得晶体在动量空间中的结构得以描述。
晶体具有动量离散化的性质,电子、声子等载流子在动量空间中的行为可以通过倒格子点阵的形态和性质来理解和
分析。
3.描述布里渊区和能带结构:倒格子点阵的布里渊区(Brillouin Zone)是动量空间中与晶格有关的基本单元。
布里渊区的形状和大小直接决定了电子能带结构、光学性质和输运特性等重要物理现象。
4.反映物质衍射性质:倒格子点阵的概念是描述晶体衍射的基础。
实验中利用晶体的衍射现象可以确定物质的结构和性质,倒格子点阵提供了理论上的基础框架。
倒格子点阵在固体物理学中具有重要的物理意义,它是描述晶体结构和性质的关键概念,并与动量空间、能带结构、衍射性质等密切相关。
通过倒格子点阵的分析,可以深入理解晶体的属性和行为,为研究材料科学和固体物理学提供了有力的工具和理论基础。


中文名称:倒格子英文名称:Reciprocal lattice术语来源:固体物理学倒格子,亦称倒易格子(点阵),它在固体物理学中,特别是在晶格动力学理论、晶体电子论以及晶体衍射方面有着较为广泛的应用。
1定义假定晶格点阵基矢a1、a2、a3(1、2、3表示 a 的下标,粗体字表示a1 是矢量,以下类同)定义一个空间点阵,我们称之为正点阵或正格子,若定义b1 = 2 π ( a2× a3) /νb2 = 2 π ( a3× a1) /νb3 = 2 π ( a1× a2) /ν其中 v = a1· ( a2× a3 ) 为正点阵原胞的体积,新的点阵的基矢b1、b2、b3是不共面的,因而由b1、b2、b3也可以构成一个新的点阵,我们称之为倒格子,而b1、b2、b3 称为倒格子基矢。
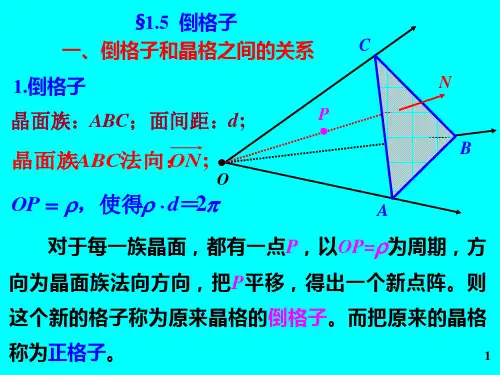
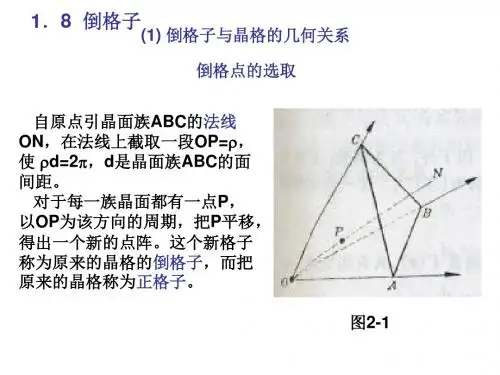
2性质1. 倒格子的一个矢量是和晶格原胞中一组晶面相对应的,它的方向是该晶面的法线方向,而它的大小则为该晶面族面间距倒数的2π倍。
2. 由倒格子的定义,不难得到下面的关系a i ·b j = 2 πδij3. 设倒格子与正点阵(格子)中的位置矢量分别为G = αb1+ βb2 + γb3R = ηa1 + θa2 + λa3 (α,η,β,θ,γ,λ皆为整数)不难证明G·R = 2π ( αη + βθ +γλ ) = 2π n,其中n为整数。
4. 设倒格子原胞体积为ψ,正格子原胞体积为 v ,根据倒格子基矢的定义,并利用矢量乘法运算知识,则可得到ψ v = ( 2 π )^3.5. 正格子晶面族(αβγ)与倒格子矢量G = αb1+ βb2 + γb3 正交(具体的内容及证明过程,请参考文献[1])3倒格子引入的意义这里简单的说一点,如上面的性质1,倒格子中的一个基矢对应于正格子中的一族晶面,也就是说,晶格中的一族晶面可以转化为倒格子中的一个点,这在处理晶格的问题上有很大的意义。


h t t p ://10.107.0.68/~j g c h e /倒格子1上讲回顾•用轨道物理学理解晶体中原子近程结构*原子轨道之间相互作用由原子轨道角分布决定*为适应周围化学环境,与邻近原子成键,原子轨道可以杂化(重组) 以适应环境 杂化最大方向由价电子数、配位、键上电子转移等共同决定*键合分类:离子、共价、金属、分子和氢键h t t p ://10.107.0.68/~j g c h e /倒格子2本讲内容•在k 空间看晶体结构*倒格子(r e c i p r o c a l l a t t i c e )倒格子基矢*正格子(d i r e c t l a t t i c e )和倒格子之间的关系h t t p ://10.107.0.68/~j g c h e /倒格子3第11讲、倒格子1.为什么倒空间?2.晶格的F o u r i e r 变换3.倒格子4.二维倒格子5.正、倒格子对应关系6.重要的例子7.B r i l l i o u n 区8.X 射线晶体衍射实验h t t p ://10.107.0.68/~j g c h e /倒格子41、为什么倒空间(r e c i p r o c a l s p a c e )?•一个物理问题,既可以在正(实,坐标)空间描写,也可以在倒(动量)空间描写*坐标表象r ,动量表象k•为什么选择不同的表象?*适当地选取一个表象,可使问题简化容易处理*比如电子在均匀空间运动,虽然坐标一直变化,但k 守衡,这时在坐标表象当然不如在动量表象简单•正空间的格矢(R l )描写周期性;在动量空间?•这两个空间完全是等价的*只是一个变换h t t p ://10.107.0.68/~j g c h e /倒格子8看格点的F o u r i e r 变换?•数学上如何用一个函数来描写格点?•δ函数!()∑-=ll R R r r δρ)(•对这个函数进行F o u r i e r 变换()()∑∑⎰⎰∙-∙-∙-=-==llli i l i ed ed eR R k R r k rk r R r r r k δρρ)(•格点满足平移周期性,则有K h 满足ml h π2=∙R K •那么乘上不变因子()∑∑∙--∙-==llh lli i eeR R K k R R k k ρh t t p ://10.107.0.68/~j g c h e /倒格子9•这告诉了我们什么信息,K h 对应什么?•坐标空间里,δ(r -R l )函数表示在R l 的格点,当满足上述条件时,其F o u r i e r 变换也是δ(k -K h )函数,表示的是倒空间里的一个点!•后面会知道,这些点就是倒格点,K h 即倒格矢*或者说前面K h 与R l 的关系定义了倒格矢,满足上述条件矢量就是倒格矢←→格矢*K h 的量纲为R l 的倒数•利用P o i s s o n 求和公式,即可得()()∑∑-==∙--hl lh h i e K R R K k k K k δρ•即当矢量K h 与R l 乘积是2π的整数倍时,在坐标空间R l 处的δ函数的F o u r i e r 变换为在动量空间以K h 为中心的δ函数!h t t p ://10.107.0.68/~j g c h e /倒格子103、倒格子(r e c i p r o c a l l a t t i c e )1=∙lh i e R K 为整数m m l h ,2π=∙R K •因此,B r a v a i s 格子也称为正格子(d i r e c t l a t t i c e )•等价关系:知道K h ,就知道R l ;反过来也一样•它们满足F o u r i e r 变换关系,因此,倒空间也称F o u r i e r 空间•定义:对B r a v a i s 格子中所有的格矢R l ,有一系列动量空间矢量K h ,满足的全部端点K h 的集合,构成该B r a v a i s 格子的倒格子,这些点称为倒格点,K h 称为倒格矢h t t p ://10.107.0.68/~j g c h e /倒格子11倒格子基矢•对正格子332211a a a R l l l l ++=•如果选择一组b ,使332211b b b K h h h h ++=•那么矢量K 就可由b 组成i jj i πδ2=⋅a b ml l l h h h l h π2332211=⋅+⋅+⋅=⋅a K a K a K R K •有•它满足上述关系,因此K h 具有平移对称性→可用基矢和整数表示的平移周期性→K h 定义倒空间的B r a v a i s 格子,b i 就是倒格子基矢•K h 为倒格矢——K h 所有的端点即为倒格点h t t p ://10.107.0.68/~j g c h e /倒格子21等价的周期性•如果K h 是倒格矢,那么物理量的F o u r i e r 级数在晶体任何平移变换下具有所期待的不变性∑+∙=+hi l l h h eF F )()(R r K K R r )(r rK K F e F hi h h ==∑∙是哪个晶面?互质?它属于哪族晶面?*是红色的这个晶面。

证明正格矢和倒格矢的关系正格矢和倒格矢是固体物理中用于描述晶体结构的两个重要的概念。
正格矢表示晶体中原子位置的空间周期性排列,而倒格矢则表示正格矢所描述的周期性结构在动量空间中的周期性。
晶体是由周期性重复单元组成的,这些单元以一定的间隔沿着晶体的各个方向排列。
这个规则的周期性排列可以用正格矢来描述。
正格矢是指晶体中原子位置的空间周期性排列,通常用一个小数定义。
在一个立方晶体中,可以将正格矢表示为n1a1 + n2a2 + n3a3,其中n1、n2、n3是整数,a1、a2、a3是三条无关联的基矢。
倒格矢是对正格矢所描述的周期性结构在动量空间中的周期性的表示。
在倒空间中,倒格矢的数目与晶体的维数相同。
通常用G来表示倒格矢。
在一个立方晶体中,倒格矢可以表示为n'1b1 + n'2b2 + n'3b3,其中n'1、n'2、n'3是整数,b1、b2、b3是三条无关联的倒空间基矢。
在晶体中,存在一个映射关系将正格矢和倒格矢联系起来。
这个关系可以通过傅里叶变换来描述。
傅里叶变换是一种数学变换,它将一个函数从时间域转换到频域或者将一个函数从空间域转换到动量域。
晶体结构中的周期性排列可以通过傅里叶变换将其转化为动量空间中的周期性。
具体来说,在周期性结构中,可以将位置空间中的函数f(r)表示为傅里叶级数的形式:f(r) = ∑g(G) * e^(iGr)其中G为倒格矢,g(G)称为结构因子,表示晶体中每个位置的复振幅。
e^(iGr)为平面波的形式,G·r为内积。
通过上述的傅里叶变换关系,可以看出正格矢和倒格矢之间存在一个简单的关系,即正格矢和倒格矢的内积为2π。
因此,可以得到如下关系:G·R = 2π(N-M)其中R为正格矢,G为倒格矢,N和M为整数。
这个关系说明了正格矢和倒格矢之间的联系。
总结起来,正格矢和倒格矢是固体物理中用于描述晶体结构的两个重要概念。

倒格子题目:试论倒格子、倒格子空间的基本概念、与正格子的关系以及在固体物理研究中的意义和作用。
1.倒格子的基本概念:假定晶格点阵基矢1a 、2a 、3a(1、2、3表示 a 的下标)定义一个空间点阵,我们称之为正点阵或正格子,若定义: v a a b )(2321 ⨯=π v a a b )(2232 ⨯=π v a a b )(2213 ⨯=π其中)(321a a a v ⨯⋅= 为正点阵原胞的体积,新的点阵的基矢1b 、2b 、3b 是不共面的,因而由 1b 、2b 、3b 也可以构成一个新的点阵,我们称之为倒格子 ,而1b 、2b 、3b 称为倒格子基矢。
2.倒格子与正格子之间的关系:①基矢间关系:3,2,1,)(0)(2=⎩⎨⎧≠==*j i j i j i b a j i π ②位矢之间关系:正格子位矢:332211a l a l a l R l ++=倒格子位矢:332211b n b n b n G n ++=二者关系:m R G l n π2=⋅ (m 为整数)表明:若两矢量点积为π2的整数倍,则其中一个矢量为正格子位矢, 另一个必为倒格子位矢。
③原胞体积的关系:倒格子原胞的体积v *与正格子原胞体积v 的关系 为:)()2()2()(32133321*a a a vb b b v ⨯⋅==⨯⋅=ππ ④倒格矢332211b h b h b h G ++=与正格子中密勒指数为)(321h h h 的晶面族正交。
即332211b h b h b h G ++=沿晶面族)(321h h h 的法线方向。
3.固体物理研究中的意义和作用:①:倒格子中的一个基矢对应于正格子中的一族晶面,也就是说,晶格中的一族晶面可以转化为倒格子中的一个点,这在处理晶格的问题上有很大的意义。
例如,晶体的衍射是由于某种波和晶格互相作用,与一族晶面发生干涉的结果,并在照片上得出一点,所以,利用倒格子来描述晶格衍射的问题是极为直观和简便的。
倒格矢与正格矢的表达式倒格矢与正格矢是固体物理学中常用的概念,用于描述晶体中的电子结构。
倒格矢是晶体中的布拉格平面的法向量,而正格矢则是晶体的晶格向量。
在本文中,将详细介绍倒格矢与正格矢的表达式及其在固体物理学中的应用。
我们来看倒格矢的表达式。
在布拉格衍射理论中,倒格矢用来描述晶体中的衍射现象。
倒格矢的表达式为:G = h*a* + k*b* + l*c*其中,G为倒格矢,h、k、l为整数,a*、b*、c*为正格矢的倒数,即与晶格向量相互垂直的向量。
倒格矢G的方向与晶格平面的法向量相同。
接下来,我们来看正格矢的表达式。
正格矢用来描述晶体的晶格结构,表达式为:R = h*a + k*b + l*c其中,R为正格矢,h、k、l为整数,a、b、c为晶格向量。
正格矢R的方向与晶格平面平行。
倒格矢与正格矢之间存在一种重要的关系,即布拉格定理。
布拉格定理表明,倒格矢和正格矢之间的内积等于一个常数,即:G·R = 2πn其中,n为整数。
这个定理揭示了倒格矢和正格矢之间的对偶性。
在固体物理学中,倒格矢和正格矢的概念广泛应用于描述晶体中的电子结构。
根据布洛赫定理,晶体中的电子波函数可以表示为平面波和周期函数的乘积形式。
在这个表达式中,平面波的波矢k可以用倒格矢G来表示,即:k = G + k'其中,k'为倒格矢的一个平移矢量。
这个表达式说明了倒格矢G和电子波矢k之间的关系。
利用倒格矢和正格矢的概念,可以方便地描述晶体中的电子结构和晶格结构。
例如,在固体能带理论中,可以通过计算倒格矢和正格矢之间的内积来得到电子能带结构。
倒格矢和正格矢的选择对于能带结构的计算结果具有重要影响。
倒格矢和正格矢还广泛应用于X射线衍射和中子衍射等实验技术中。
通过测量衍射角度和晶格常数,可以确定倒格矢和正格矢之间的关系,从而得到晶体结构的信息。
在总结一下,倒格矢和正格矢是固体物理学中重要的概念,用于描述晶体中的电子结构和晶格结构。
证明正格矢和倒格矢的关系正格矢和倒格矢是固体物理学中两个非常重要的概念,它们之间有着紧密的关系。
本文将从生动、全面、有指导意义的角度来证明这一关系。
首先,我们需要先了解正格矢和倒格矢的定义。
正格矢是描述晶体中原子位置的矢量,它是最小的平移对称操作的矢量。
在一个晶体中,如果两个位置的矢量之差等于正格矢,那么这两个位置上的原子是等同的。
倒格矢则是描述晶体中平移对称的倒数的矢量,它是波矢的实空间表象。
正格矢和倒格矢的关系可以通过傅里叶变换来得到证明。
傅里叶变换是一种将函数从时间或空间域转换到频率或波数域的数学工具。
在固体物理学中,我们经常使用傅里叶变换来描述周期性结构。
正是因为晶体的周期性,我们才能够将实空间中的波函数用倒空间的波函数来表示。
傅里叶变换的公式为:\[F(q) = \int f(x) e^{-2\pi i x \cdot q} dx\]其中,\(F(q)\)是倒空间中的波函数,\(f(x)\)是实空间中的波函数,\(q\)是波矢。
在晶体中,我们假设晶格的原胞大小为\(a\),则正格矢可以表示为:\[R = n_1 \mathbf{a_1} + n_2 \mathbf{a_2} + n_3\mathbf{a_3}\]其中,\(\mathbf{a_1}\),\(\mathbf{a_2}\)和\(\mathbf{a_3}\)是晶格的基矢,而\(n_1\),\(n_2\)和\(n_3\)是整数。
这样,我们可以将正格矢用指数形式表示为:\[e^{2\pi i R \cdot q} = e^{2\pi i (n_1 \mathbf{a_1} +n_2 \mathbf{a_2} + n_3 \mathbf{a_3}) \cdot q} = e^{2\pi i(n_1 \mathbf{a_1} \cdot q + n_2 \mathbf{a_2} \cdot q + n_3\mathbf{a_3} \cdot q)}\]根据晶体的周期性,正格矢的指数函数是周期性的,即:\[e^{2\pi i R \cdot q} = e^{2\pi i (n_1 \mathbf{a_1}\cdot q + n_2 \mathbf{a_2} \cdot q + n_3 \mathbf{a_3} \cdot q)} = 1\]也就是说,正格矢的指数函数在倒格矢上是平凡的。